Chào mừng các em học sinh đến với bài học về Dạng 4: Xác suất thực nghiệm, thuộc Chủ đề 11 trong chương trình Ôn hè Toán 6 của giaitoan.edu.vn. Bài học này sẽ giúp các em hiểu rõ khái niệm xác suất thực nghiệm và cách áp dụng nó vào giải quyết các bài toán thực tế.
Chúng ta sẽ cùng nhau tìm hiểu về cách thu thập dữ liệu, tính toán xác suất dựa trên dữ liệu đó, và phân tích kết quả để đưa ra những kết luận hợp lý. Giaitoan.edu.vn cam kết mang đến cho các em những bài giảng dễ hiểu, bài tập phong phú và phương pháp học tập hiệu quả.
I. Khả năng xảy ra của một sự kiện Khả năng của một sự kiện được thể hiện bằng một con số từ 0 đến 1.
I. Khả năng xảy ra của một sự kiện
Khả năng của một sự kiện được thể hiện bằng một con số từ 0 đến 1.
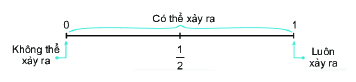
Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.
Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.
II. Xác suất thực nghiệm
Thực hiện lặp đi lặp lại một hoạt động nào đó n lần.
Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số
\(\dfrac{{n(A)}}{n} = \) Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động
Được gọi là xác suất thực nghiệm của sự kiện A.
Nhận xét:Xác suất thực nghiệm phụ thuộc vào người thực hiện thí nghiệm, trò chơi và số lần người đó thực hiện thí nghiệm, trò chơi.
Bài 1:
Bài toán “Ước lượng số cá trong hồ”
- Sau khoảng thời gian nuôi cá, những người cư dân muốn biết xem số cá hiện có trong hồ là bao nhiêu để có những kế hoạch nuôi đúng cách. Vấn đề đặt ra là không thể bắt hết cá lên bờ, rồi sau đó đếm thủ công được, sẽ ảnh hưởng không tốt đến cá. Hãy xét một giải pháp sau đây.
- Đầu tiên, bác Thắng, một ngư dân có kinh nghiệm, bắt 60 con cá lên và đánh dấu, sau đó thả lại vào hồ. Ngày hôm sau, bác Thắng bắt lên 24 con cá và đếm được 3 con cá đã được đánh dấu.
a) Tính xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu”
b) Giải thích vì sao từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ? Hãy ước tính số cá trong hồ.
Bài 2:
Tổng hợp kết quả xét nghiệm Covid ở một bệnh viện trong \(4\) ngày ta thu được bảng sau:

a) Hãy tính xác suất thực nghiệm của sự kiện một ca xét nghiệm có kết quả dương tính theo từng ngày
b) Hãy tính tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày.
Câu 3:
Hàng ngày Sơn đều đi xe buýt tới trường. Sơn ghi lại thời gian chờ xe của mình trong \(20\) lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:
a) Sơn phải chờ xe dưới \(1\) phút
b) Sơn phải chờ xe từ \(5\) phút trở lên
Lời giải chi tiết:
Bài 1:
Bài toán “Ước lượng số cá trong hồ”
- Sau khoảng thời gian nuôi cá, những người cư dân muốn biết xem số cá hiện có trong hồ là bao nhiêu để có những kế hoạch nuôi đúng cách. Vấn đề đặt ra là không thể bắt hết cá lên bờ, rồi sau đó đếm thủ công được, sẽ ảnh hưởng không tốt đến cá. Hãy xét một giải pháp sau đây.
- Đầu tiên, bác Thắng, một ngư dân có kinh nghiệm, bắt 60 con cá lên và đánh dấu, sau đó thả lại vào hồ. Ngày hôm sau, bác Thắng bắt lên 24 con cá và đếm được 3 con cá đã được đánh dấu.
a) Tính xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu”
b) Giải thích vì sao từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ? Hãy ước tính số cá trong hồ.
Phương pháp
Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm.
Lời giải
a) Xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu” là: \(\dfrac{3}{{24}} = 12,5\% \)
b) Từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ như sau:
Trong số cá bắt lên, số cá được đánh dấu chiếm 12,5%
Toàn bộ số cá được đánh dấu trong hồ là 60 con
Có thể ước lượng 60 con được đánh dấu này tương ứng với 12,5% số cá trong hồ
Vậy, ước lượng được số cá trong hồ là: \(60:12,5\% = 480\)\(\left( {{\rm{con}}} \right)\)
Bài 2:
Tổng hợp kết quả xét nghiệm Covid ở một bệnh viện trong \(4\) ngày ta thu được bảng sau:

a) Hãy tính xác suất thực nghiệm của sự kiện một ca xét nghiệm có kết quả dương tính theo từng ngày
b) Hãy tính tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày.
Phương pháp
Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm
Lời giải
a) Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ nhất” là:
\(\dfrac{{15}}{{150}} = \dfrac{1}{{10}}\)
Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ hai” là: \(\dfrac{{21}}{{200}}\)
Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ ba” là: \(\dfrac{{17}}{{180}}\)
Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ ba” là:
\(\dfrac{{24}}{{220}} = \dfrac{6}{{55}}\)
b) Tổng số ca dương tính trong \(4\) ngày là: \(15 + 21 + 17 + 24 = 77\)
Tổng số ca xét nghiệm trong \(4\) ngày là: \(150 + 200 + 180 + 220 = 750\)
Tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày là: \(\dfrac{{77}}{{750}}\)
Câu 3:
Hàng ngày Sơn đều đi xe buýt tới trường. Sơn ghi lại thời gian chờ xe của mình trong \(20\) lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:
a) Sơn phải chờ xe dưới \(1\) phút
b) Sơn phải chờ xe từ \(5\) phút trở lên
Phương pháp
Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm
Lời giải
a) Xác suất thực nghiệm của sự kiện: “Sơn phải chờ xe dưới \(1\) phút” là \(\dfrac{4}{{20}} = \dfrac{1}{5}\)
b) Số lần Sơn phải chờ xe từ \(5\) phút trở lên là: \(4 + 2 = 6\)
Xác suất thực nghiệm của sự kiện:” Sơn phải chờ xe từ \(5\) phút trở lên” là \(\dfrac{6}{{20}} = \dfrac{3}{{10}}\)
I. Khả năng xảy ra của một sự kiện
Khả năng của một sự kiện được thể hiện bằng một con số từ 0 đến 1.
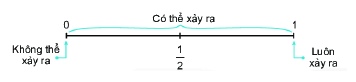
Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.
Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.
II. Xác suất thực nghiệm
Thực hiện lặp đi lặp lại một hoạt động nào đó n lần.
Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số
\(\dfrac{{n(A)}}{n} = \) Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động
Được gọi là xác suất thực nghiệm của sự kiện A.
Nhận xét:Xác suất thực nghiệm phụ thuộc vào người thực hiện thí nghiệm, trò chơi và số lần người đó thực hiện thí nghiệm, trò chơi.
Bài 1:
Bài toán “Ước lượng số cá trong hồ”
- Sau khoảng thời gian nuôi cá, những người cư dân muốn biết xem số cá hiện có trong hồ là bao nhiêu để có những kế hoạch nuôi đúng cách. Vấn đề đặt ra là không thể bắt hết cá lên bờ, rồi sau đó đếm thủ công được, sẽ ảnh hưởng không tốt đến cá. Hãy xét một giải pháp sau đây.
- Đầu tiên, bác Thắng, một ngư dân có kinh nghiệm, bắt 60 con cá lên và đánh dấu, sau đó thả lại vào hồ. Ngày hôm sau, bác Thắng bắt lên 24 con cá và đếm được 3 con cá đã được đánh dấu.
a) Tính xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu”
b) Giải thích vì sao từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ? Hãy ước tính số cá trong hồ.
Bài 2:
Tổng hợp kết quả xét nghiệm Covid ở một bệnh viện trong \(4\) ngày ta thu được bảng sau:

a) Hãy tính xác suất thực nghiệm của sự kiện một ca xét nghiệm có kết quả dương tính theo từng ngày
b) Hãy tính tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày.
Câu 3:
Hàng ngày Sơn đều đi xe buýt tới trường. Sơn ghi lại thời gian chờ xe của mình trong \(20\) lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:
a) Sơn phải chờ xe dưới \(1\) phút
b) Sơn phải chờ xe từ \(5\) phút trở lên
Lời giải chi tiết:
Bài 1:
Bài toán “Ước lượng số cá trong hồ”
- Sau khoảng thời gian nuôi cá, những người cư dân muốn biết xem số cá hiện có trong hồ là bao nhiêu để có những kế hoạch nuôi đúng cách. Vấn đề đặt ra là không thể bắt hết cá lên bờ, rồi sau đó đếm thủ công được, sẽ ảnh hưởng không tốt đến cá. Hãy xét một giải pháp sau đây.
- Đầu tiên, bác Thắng, một ngư dân có kinh nghiệm, bắt 60 con cá lên và đánh dấu, sau đó thả lại vào hồ. Ngày hôm sau, bác Thắng bắt lên 24 con cá và đếm được 3 con cá đã được đánh dấu.
a) Tính xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu”
b) Giải thích vì sao từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ? Hãy ước tính số cá trong hồ.
Phương pháp
Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm.
Lời giải
a) Xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu” là: \(\dfrac{3}{{24}} = 12,5\% \)
b) Từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ như sau:
Trong số cá bắt lên, số cá được đánh dấu chiếm 12,5%
Toàn bộ số cá được đánh dấu trong hồ là 60 con
Có thể ước lượng 60 con được đánh dấu này tương ứng với 12,5% số cá trong hồ
Vậy, ước lượng được số cá trong hồ là: \(60:12,5\% = 480\)\(\left( {{\rm{con}}} \right)\)
Bài 2:
Tổng hợp kết quả xét nghiệm Covid ở một bệnh viện trong \(4\) ngày ta thu được bảng sau:

a) Hãy tính xác suất thực nghiệm của sự kiện một ca xét nghiệm có kết quả dương tính theo từng ngày
b) Hãy tính tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày.
Phương pháp
Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm
Lời giải
a) Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ nhất” là:
\(\dfrac{{15}}{{150}} = \dfrac{1}{{10}}\)
Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ hai” là: \(\dfrac{{21}}{{200}}\)
Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ ba” là: \(\dfrac{{17}}{{180}}\)
Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ ba” là:
\(\dfrac{{24}}{{220}} = \dfrac{6}{{55}}\)
b) Tổng số ca dương tính trong \(4\) ngày là: \(15 + 21 + 17 + 24 = 77\)
Tổng số ca xét nghiệm trong \(4\) ngày là: \(150 + 200 + 180 + 220 = 750\)
Tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày là: \(\dfrac{{77}}{{750}}\)
Câu 3:
Hàng ngày Sơn đều đi xe buýt tới trường. Sơn ghi lại thời gian chờ xe của mình trong \(20\) lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:
a) Sơn phải chờ xe dưới \(1\) phút
b) Sơn phải chờ xe từ \(5\) phút trở lên
Phương pháp
Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm
Lời giải
a) Xác suất thực nghiệm của sự kiện: “Sơn phải chờ xe dưới \(1\) phút” là \(\dfrac{4}{{20}} = \dfrac{1}{5}\)
b) Số lần Sơn phải chờ xe từ \(5\) phút trở lên là: \(4 + 2 = 6\)
Xác suất thực nghiệm của sự kiện:” Sơn phải chờ xe từ \(5\) phút trở lên” là \(\dfrac{6}{{20}} = \dfrac{3}{{10}}\)
Xác suất thực nghiệm là một khái niệm quan trọng trong toán học, giúp chúng ta dự đoán khả năng xảy ra của một sự kiện dựa trên kết quả của các thử nghiệm thực tế. Trong chương trình Ôn hè Toán 6, Chủ đề 11 tập trung vào việc giới thiệu khái niệm này một cách trực quan và dễ hiểu.
Xác suất thực nghiệm của một sự kiện A được tính bằng tỉ số giữa số lần sự kiện A xảy ra và tổng số lần thực hiện thử nghiệm. Công thức tính xác suất thực nghiệm như sau:
P(A) = (Số lần sự kiện A xảy ra) / (Tổng số lần thực hiện thử nghiệm)
Ví dụ: Nếu chúng ta tung một đồng xu 100 lần và mặt ngửa xuất hiện 52 lần, thì xác suất thực nghiệm của sự kiện “mặt ngửa xuất hiện” là 52/100 = 0.52.
Để tính xác suất thực nghiệm, chúng ta cần thu thập dữ liệu từ các thử nghiệm thực tế. Dữ liệu này có thể được thu thập thông qua các hoạt động như:
Sau khi thu thập đủ dữ liệu, chúng ta có thể áp dụng công thức trên để tính toán xác suất thực nghiệm của các sự kiện khác nhau.
Ví dụ 1: Một hộp có 10 quả bóng, trong đó có 3 quả bóng màu đỏ, 4 quả bóng màu xanh và 3 quả bóng màu vàng. Nếu chúng ta lấy ngẫu nhiên 1 quả bóng từ hộp, tính xác suất thực nghiệm để lấy được quả bóng màu đỏ.
Giải:
Tổng số quả bóng trong hộp là 10.
Số quả bóng màu đỏ là 3.
Xác suất thực nghiệm để lấy được quả bóng màu đỏ là 3/10 = 0.3.
Ví dụ 2: Một học sinh thực hiện một bài kiểm tra trắc nghiệm gồm 20 câu hỏi. Học sinh đó trả lời đúng 15 câu. Tính xác suất thực nghiệm để học sinh đó trả lời đúng một câu hỏi bất kỳ.
Giải:
Tổng số câu hỏi trong bài kiểm tra là 20.
Số câu học sinh trả lời đúng là 15.
Xác suất thực nghiệm để học sinh trả lời đúng một câu hỏi bất kỳ là 15/20 = 0.75.
Xác suất thực nghiệm có nhiều ứng dụng trong thực tế, bao gồm:
Để củng cố kiến thức về xác suất thực nghiệm, các em hãy làm các bài tập sau:
Xác suất thực nghiệm là một công cụ hữu ích để dự đoán khả năng xảy ra của một sự kiện dựa trên kết quả của các thử nghiệm thực tế. Việc hiểu rõ khái niệm này và cách áp dụng nó vào giải quyết các bài toán thực tế là rất quan trọng trong học tập và cuộc sống.
Giaitoan.edu.vn hy vọng bài học này đã giúp các em nắm vững kiến thức về Dạng 4: Xác suất thực nghiệm - Chủ đề 11 Ôn hè Toán 6. Chúc các em học tập tốt!