Chủ đề này thuộc chương trình Ôn hè Toán 6, đóng vai trò quan trọng trong việc xây dựng nền tảng kiến thức số học. Việc nắm vững phương pháp phân tích một số ra thừa số nguyên tố giúp học sinh giải quyết các bài toán liên quan đến ước, bội, và các khái niệm toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, bài tập đa dạng và phương pháp giải chi tiết để giúp học sinh hiểu rõ và tự tin chinh phục dạng toán này.
* Cách 1: Phân tích bằng sơ đồ cây:
* Cách 1: Phân tích bằng sơ đồ cây:
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
* Cách 2: Phân tích bằng sơ đồ cột:
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Bài 1:
Phân tích các số 315, 150, 213 ra thừa số nguyên tố.
Bài 2:
Có bao nhiêu số tự nhiên là ước của 312.
Lời giải chi tiết:
Bài 1:
Phân tích các số 315, 150, 213 ra thừa số nguyên tố.
Phương pháp
* Cách 1: Phân tích bằng sơ đồ cây:
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
* Cách 2: Phân tích bằng sơ đồ cột:
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Lời giải
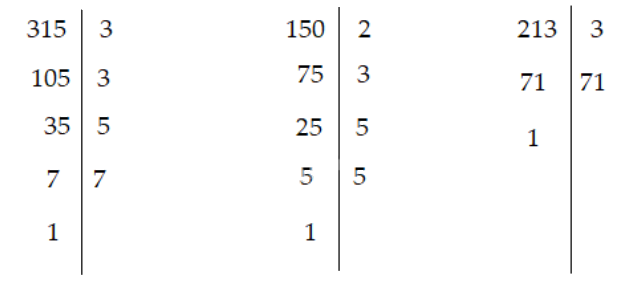
Vậy:
\(\begin{array}{l}315 = {3^2}.5.7;\\150 = {2.3.5^2};\\213 = 3.71.\end{array}\)
Bài 2:
Có bao nhiêu số tự nhiên là ước của 312.
Phương pháp
Bước 1: Phân tích số 312 ra thừa số nguên tố.
Bước 2: Nếu \(a = {p^k}.{q^j}...{r^l}\) thì a có số ước (là số tự nhiên) là: (k+1) . (j + 1) … (l + 1)
Lời giải

Ta được: 312 = 23 . 3 . 13.
Vậy số ước ( là số tự nhiên) của 312 là: (3 + 1) . (1 + 1) . (1 + 1) = 16.
* Cách 1: Phân tích bằng sơ đồ cây:
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
* Cách 2: Phân tích bằng sơ đồ cột:
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Bài 1:
Phân tích các số 315, 150, 213 ra thừa số nguyên tố.
Bài 2:
Có bao nhiêu số tự nhiên là ước của 312.
Lời giải chi tiết:
Bài 1:
Phân tích các số 315, 150, 213 ra thừa số nguyên tố.
Phương pháp
* Cách 1: Phân tích bằng sơ đồ cây:
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
* Cách 2: Phân tích bằng sơ đồ cột:
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Lời giải
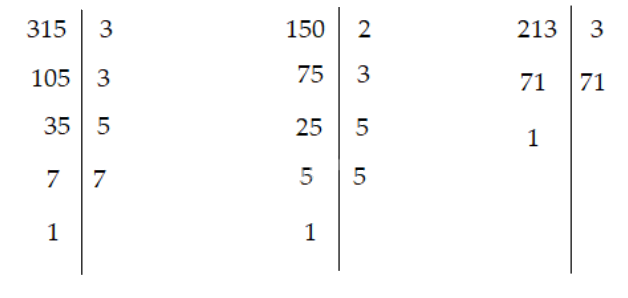
Vậy:
\(\begin{array}{l}315 = {3^2}.5.7;\\150 = {2.3.5^2};\\213 = 3.71.\end{array}\)
Bài 2:
Có bao nhiêu số tự nhiên là ước của 312.
Phương pháp
Bước 1: Phân tích số 312 ra thừa số nguên tố.
Bước 2: Nếu \(a = {p^k}.{q^j}...{r^l}\) thì a có số ước (là số tự nhiên) là: (k+1) . (j + 1) … (l + 1)
Lời giải
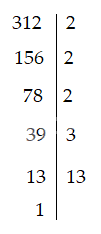
Ta được: 312 = 23 . 3 . 13.
Vậy số ước ( là số tự nhiên) của 312 là: (3 + 1) . (1 + 1) . (1 + 1) = 16.
Phân tích một số ra thừa số nguyên tố là một kỹ năng cơ bản và quan trọng trong chương trình Toán 6. Nó giúp học sinh hiểu rõ cấu trúc của các số tự nhiên và là nền tảng cho nhiều kiến thức toán học khác. Dưới đây là hướng dẫn chi tiết về cách phân tích một số ra thừa số nguyên tố, cùng với các ví dụ minh họa và bài tập thực hành.
Số nguyên tố là số tự nhiên lớn hơn 1, chỉ chia hết cho 1 và chính nó. Ví dụ: 2, 3, 5, 7, 11, 13,...
Phân tích một số ra thừa số nguyên tố là viết số đó dưới dạng tích của các số nguyên tố. Ví dụ: 12 = 2 x 2 x 3 = 22 x 3.
Có hai phương pháp chính để phân tích một số ra thừa số nguyên tố:
Sử dụng phương pháp chia liên tiếp:
Vậy, 36 = 2 x 2 x 3 x 3 = 22 x 32
Sử dụng phương pháp sơ đồ hình cây:
48 -> 2 x 24 -> 2 x 12 -> 2 x 6 -> 2 x 3
Vậy, 48 = 2 x 2 x 2 x 2 x 3 = 24 x 3
Hãy phân tích các số sau ra thừa số nguyên tố:
Việc phân tích một số ra thừa số nguyên tố có nhiều ứng dụng trong toán học, bao gồm:
Khi phân tích một số ra thừa số nguyên tố, cần lưu ý:
Phân tích một số ra thừa số nguyên tố là một kỹ năng quan trọng trong Toán 6. Việc luyện tập thường xuyên và nắm vững phương pháp sẽ giúp học sinh giải quyết các bài toán một cách nhanh chóng và chính xác. Chúc các em học tốt!