Chào mừng các em học sinh đến với bài học về Dạng 1. Viết tập hợp, thuộc Chủ đề 1 của chương trình ôn hè Toán 6. Bài học này sẽ giúp các em nắm vững khái niệm cơ bản về tập hợp, cách viết và nhận biết các phần tử của tập hợp.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với hệ thống bài tập đa dạng, giúp các em tự tin chinh phục môn Toán.
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.
Phần tử x thuộc tập hợp A được kí hiệu là \(x \in A\), y không thuộc tập hợp A được kí hiệu là \(y \notin A\)
Ta thường viết tập hợp theo 2 cách:
Cách 1: Liệt kê các phần tử của tập hợp
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
Bài 1: Cho tập hợp P là tập hợp các chữ cái có trong từ NGÂN HÀNG
a) Điền kí hiệu \( \in ; \notin \) thích hợp vào ô trống
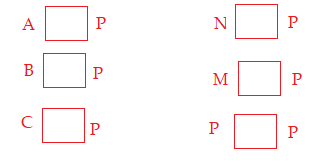
b) Viết tập hợp P.
Bài 2: Cho B là tập hợp các số tự nhiên chẵn, nhỏ hơn 8.
Viết tập hợp B theo 2 cách
Bài 3: Cho tập hợp M = {1;2;3;4;5;6}
N = {8;7;6;5;4}
a) Viết tập hợp A gồm các phần tử thuộc cả M và N
b) Viết tập hợp B gồm các phần tử thuộc M nhưng không thuộc N
c) Viết tập hợp C gồm các phần tử thuộc N nhưng không thuộc M
Lời giải chi tiết:
Bài 1: Cho tập hợp P là tập hợp các chữ cái có trong từ NGÂN HÀNG
a) Điền kí hiệu \( \in ; \notin \) thích hợp vào ô trống
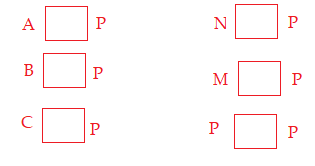
b) Viết tập hợp P.
Phương pháp
Phần tử x thuộc tập hợp A được kí hiệu là \(x \in A\), y không thuộc tập hợp A được kí hiệu là \(y \notin A\)
Viết tập hợp bằng cách liệt kê các phần tử của tập hợp
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Lời giải
a)
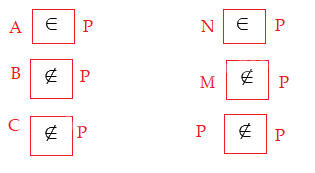
b) P = {N;G;Â;H;A}
Bài 2: Cho B là tập hợp các số tự nhiên chẵn, nhỏ hơn 8.
Viết tập hợp B theo 2 cách
Phương pháp
Cách 1: Liệt kê các phần tử của tập hợp
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó
Lời giải
Cách 1:
B = {0;2;4;6}
Cách 2:
B = {x \( \in \)N| x là số chẵn nhỏ hơn 8}
Bài 3: Cho tập hợp M = {1;2;3;4;5;6}
N = {8;7;6;5;4}
a) Viết tập hợp A gồm các phần tử thuộc cả M và N
b) Viết tập hợp B gồm các phần tử thuộc M nhưng không thuộc N
c) Viết tập hợp C gồm các phần tử thuộc N nhưng không thuộc M
Phương pháp
Bước 1: Tìm các phần tử của mỗi tập hợp
Bước 2: Viết tập hợp bằng cách liệt kê các phần tử của tập hợp:
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Lời giải
a) Các phần tử thuộc cả M và N là: 4;5;6.
A = {4;5;6}
b) Các phần tử thuộc M nhưng không thuộc N là: 1;2;3
B = {1;2;3}
c) Các phần tử thuộc N nhưng không thuộc M là: 8;7.
C = {8;7}
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.
Phần tử x thuộc tập hợp A được kí hiệu là \(x \in A\), y không thuộc tập hợp A được kí hiệu là \(y \notin A\)
Ta thường viết tập hợp theo 2 cách:
Cách 1: Liệt kê các phần tử của tập hợp
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
Bài 1: Cho tập hợp P là tập hợp các chữ cái có trong từ NGÂN HÀNG
a) Điền kí hiệu \( \in ; \notin \) thích hợp vào ô trống
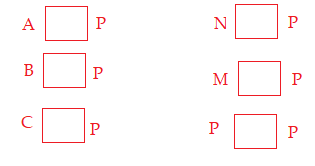
b) Viết tập hợp P.
Bài 2: Cho B là tập hợp các số tự nhiên chẵn, nhỏ hơn 8.
Viết tập hợp B theo 2 cách
Bài 3: Cho tập hợp M = {1;2;3;4;5;6}
N = {8;7;6;5;4}
a) Viết tập hợp A gồm các phần tử thuộc cả M và N
b) Viết tập hợp B gồm các phần tử thuộc M nhưng không thuộc N
c) Viết tập hợp C gồm các phần tử thuộc N nhưng không thuộc M
Lời giải chi tiết:
Bài 1: Cho tập hợp P là tập hợp các chữ cái có trong từ NGÂN HÀNG
a) Điền kí hiệu \( \in ; \notin \) thích hợp vào ô trống
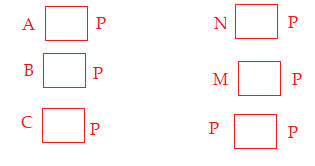
b) Viết tập hợp P.
Phương pháp
Phần tử x thuộc tập hợp A được kí hiệu là \(x \in A\), y không thuộc tập hợp A được kí hiệu là \(y \notin A\)
Viết tập hợp bằng cách liệt kê các phần tử của tập hợp
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Lời giải
a)
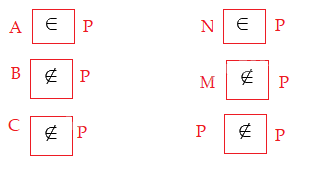
b) P = {N;G;Â;H;A}
Bài 2: Cho B là tập hợp các số tự nhiên chẵn, nhỏ hơn 8.
Viết tập hợp B theo 2 cách
Phương pháp
Cách 1: Liệt kê các phần tử của tập hợp
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó
Lời giải
Cách 1:
B = {0;2;4;6}
Cách 2:
B = {x \( \in \)N| x là số chẵn nhỏ hơn 8}
Bài 3: Cho tập hợp M = {1;2;3;4;5;6}
N = {8;7;6;5;4}
a) Viết tập hợp A gồm các phần tử thuộc cả M và N
b) Viết tập hợp B gồm các phần tử thuộc M nhưng không thuộc N
c) Viết tập hợp C gồm các phần tử thuộc N nhưng không thuộc M
Phương pháp
Bước 1: Tìm các phần tử của mỗi tập hợp
Bước 2: Viết tập hợp bằng cách liệt kê các phần tử của tập hợp:
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Lời giải
a) Các phần tử thuộc cả M và N là: 4;5;6.
A = {4;5;6}
b) Các phần tử thuộc M nhưng không thuộc N là: 1;2;3
B = {1;2;3}
c) Các phần tử thuộc N nhưng không thuộc M là: 8;7.
C = {8;7}
Tập hợp là một khái niệm nền tảng trong toán học, đặc biệt quan trọng ở chương trình Toán 6. Việc hiểu rõ cách viết và nhận biết tập hợp là bước đầu tiên để làm quen với các khái niệm toán học phức tạp hơn. Bài viết này sẽ cung cấp một cái nhìn tổng quan về Dạng 1. Viết tập hợp, Chủ đề 1 Ôn hè Toán 6, bao gồm định nghĩa, ví dụ minh họa và các bài tập thực hành.
Định nghĩa: Tập hợp là một nhóm các đối tượng được xác định rõ ràng. Các đối tượng này được gọi là các phần tử của tập hợp.
Ký hiệu: Tập hợp thường được ký hiệu bằng các chữ cái in hoa như A, B, C,...
Ví dụ:
Có hai cách chính để viết tập hợp:
Ký hiệu: ∈ (thuộc) và ∉ (không thuộc)
Ví dụ:
Bài 1: Viết tập hợp các số tự nhiên lẻ nhỏ hơn 10.
Giải: A = {1, 3, 5, 7, 9}
Bài 2: Cho tập hợp B = {a, b, c, d, e}. Hỏi các chữ cái m, n có thuộc tập hợp B không?
Giải: m ∉ B và n ∉ B
Bài 3: Mô tả tập hợp các tháng có 31 ngày bằng tính chất đặc trưng.
Giải: C = {x | x là tháng có 31 ngày}
Khái niệm tập hợp được sử dụng rộng rãi trong nhiều lĩnh vực của toán học, bao gồm:
Dạng 1. Viết tập hợp là một phần quan trọng trong chương trình Toán 6. Việc nắm vững kiến thức về tập hợp sẽ giúp các em học sinh xây dựng nền tảng vững chắc cho các bài học tiếp theo. Hãy luyện tập thường xuyên để hiểu rõ hơn về khái niệm này và áp dụng nó vào giải các bài toán thực tế.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích về Dạng 1. Viết tập hợp, Chủ đề 1 Ôn hè Toán 6. Chúc các em học tập tốt!