Chào mừng các em học sinh đến với bài học về Dạng 1: Điểm và Đường Thẳng, thuộc Chủ đề 10 trong chương trình Ôn hè Toán 6 của giaitoan.edu.vn. Đây là một trong những kiến thức nền tảng quan trọng của môn Toán, giúp các em xây dựng cơ sở vững chắc cho các bài học tiếp theo.
Trong bài học này, chúng ta sẽ cùng nhau tìm hiểu về các khái niệm cơ bản như điểm, đường thẳng, đoạn thẳng, tia, và các quan hệ giữa chúng.
1. Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
1. Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
*Điểm
Dấu chấm nhỏ là hình ảnh của điểm
Quy ước: Khi nói 2 điểm mà không nói gì thêm, ta hiểu đó là 2 điểm phân biệt
*Đường thẳng
Đường thẳng không bị giới hạn về 2 phía
*Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
Ta thường dùng chữ cái in hoa để đặt tên điểm và chữ cái thường để đặt tên đường thẳng, chẳng hạn điểm M,N,P,Q,...; đường thẳng a,b,d,...
Điểm A thuộc đường thẳng d, kí hiệu \(A \in d\)
Điểm B không đường thẳng d, kí hiệu là \(B \notin d\)
Nếu \(A \in d\), ta còn nói: Điểm A nằm trên đường thẳng d, hay đường thẳng d đi qua điểm A
Chú ý: Có vô số điểm thuộc đường thẳng
*Đường thẳng đi qua 2 điểm
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm A và B
Đường thẳng đi qua 2 điểm A, B được gọi đường thẳng AB hay đường thẳng BA
2. Điểm nằm giữa 2 điểm
+) Ba điểm phân biệt A, B, C cùng thuộc một đường thẳng được gọi là ba điểm thẳng hàng.
+) Ba điểm phân biệt D, E, F không cùng thuộc bất kì một đường thẳng nào được gọi là ba điểm không thẳng hàng.
Trong ba điểm thẳng hàng, có một điểm và chỉ một điểm nằm giữa hai điểm còn lại.
3 điểm A,B,C cùng nằm trên đường thẳng d như hình sau
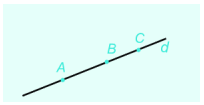
Điểm B nằm giữa 2 điểm A và C
2 điểm A và B nằm cùng phía đối với điểm C
2 điểm A và C nằm khác phía đối với điểm B
3. Tia
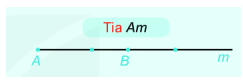
+ Tia Am gồm điểm A, điểm B và các điểm nằm cùng phía với B đối với A. Tia Am còn được kí hiệu là tia AB. Điểm A là điểm gốc của tia
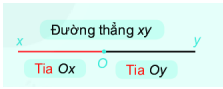
+ Điểm O nằm trên đường thẳng xy chia đường thẳng thành 2 phần. Mỗi phần đó cùng với điểm O làm thành một tia. Khi đó 2 tia Ox và Oy gọi là 2 tia đối nhau
Nhận xét:

- Nếu hai tia OA và OB đối nhau thì điểm \(O\) nằm giữa hai điểm \(A\) và \(B\)
- Ngược lại, nếu điểm \(O\) nằm giữa hai điểm \(A\) và \(B\) thì:
+ Hai tia OA;OB đối nhau
+ Hai tia AO;AB trùng nhau; hai tia BO;BA trùng nhau
Bài 1:
Cho hình vẽ:
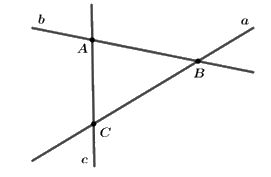
Đường thẳng nào không đi qua điểm \(A\)?
Bài 2:
Vẽ hình theo cách diễn đạt sau: Điểm \(E\) nằm trên đường thẳng \(x\) nhưng không nằm trên đường thẳng \(a\). Đường thẳng \(x\) đi qua điểm \(F\) nằm trên đường thẳng \(a\).
Bài 3:
Vẽ điểm \(C\) sao cho \(C\) thuộc đường thẳng \(xy\) và điểm \(C\) nằm giữa hai điểm \(A\) và \(B\). Kể tên các tia chung gốc \(A\) có trong hình vẽ.
Bài 4:
Cho bốn điểm \(O,M,N,P\) thỏa mãn điều kiện: Hai tia \(OM\) và \(ON\) là hai tia đối nhau, hai tia \(OM\) và \(OP\) là hai tia đối nhau.
a) Có nhận xét gì về bốn điểm \(M,N,O,P\)?
b) Điểm \(O\) nằm giữa hai điểm nào?
Lời giải chi tiết:
Bài 1:
Cho hình vẽ:
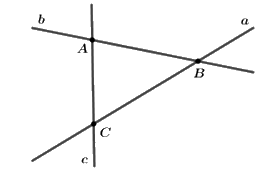
Đường thẳng nào không đi qua điểm \(A\)?
Phương pháp
Quan sát hình vẽ và tìm những đường thẳng cùng đi qua điểm \(A\).
Lời giải
Quan sát hình vẽ ta thấy: Điểm \(A\) nằm trên hai đường thẳng \(b\) và \(c\); Điểm \(A\) nằm ngoài đường thẳng \(a\).
Các đường thẳng đi qua điểm \(A\) là: Đường thẳng \(b\) và đường thẳng \(c\)
Đường thẳng \(a\) không đi qua điểm \(A\).
Bài 2:
Vẽ hình theo cách diễn đạt sau: Điểm \(E\) nằm trên đường thẳng \(x\) nhưng không nằm trên đường thẳng \(a\). Đường thẳng \(x\) đi qua điểm \(F\) nằm trên đường thẳng \(a\).
Phương pháp
+ Viết dưới dạng kí hiệu cách diễn đạt với bài bài.
+ Quan sát hình vẽ, tìm mỗi quan hệ của các điểm với từng đường thẳng.
Lời giải
Điểm \(E\) nằm trên đường thẳng \(x\) nhưng không nằm trên đường thẳng \(a\) nghĩa là: \(E \in x\) nhưng \(E \notin a\).
Đường thẳng \(x\) đi qua điểm \(F\) nằm trên đường thẳng \(a\) nghĩa là: \(F \in x\) và \(F \in a\).
Bài 3:
Vẽ điểm \(C\) sao cho \(C\) thuộc đường thẳng \(xy\) và điểm \(C\) nằm giữa hai điểm \(A\) và \(B\). Kể tên các tia chung gốc \(A\) có trong hình vẽ.
Phương pháp
Sử dụng định nghĩa hai tia đối nhau, định nghĩa về tia.
Lời giải
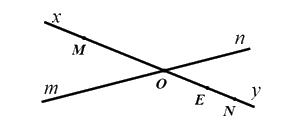
a) Các tia đối nhau trong hình vẽ là:\(Ox,Oy,Om,On\)
b) Ta có \(OM\) và \(Oy\) là hai tia đối nhau nên \(N \in Oy\) thì \(OM\) và \(ON\) là hai tia đối nhau.
Bài 4:
Cho bốn điểm \(O,M,N,P\) thỏa mãn điều kiện: Hai tia \(OM\) và \(ON\) là hai tia đối nhau, hai tia \(OM\) và \(OP\) là hai tia đối nhau.
a) Có nhận xét gì về bốn điểm \(M,N,O,P\)?
b) Điểm \(O\) nằm giữa hai điểm nào?
Phương pháp
Sử dụng khái niệm hai tia đối nhau, quan hệ giữa ba điểm thẳng hàng.
Lời giải
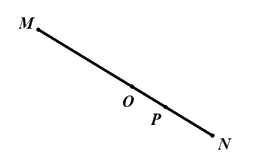
a) Ta có \(OM\) và \(ON\) là hai tia đối nhau nên ba điểm \(M,N,O\) cùng thuộc một đường thẳng,
Ta có \(OM\) và \(OP\) là hai tia đối nhau nên ba điểm \(M,O,P\) cùng thuộc một đường thẳng.
Suy ra bốn điểm \(M,N,O,P\) cùng thuộc một đường thẳng.
b) Điểm \(O\) nằm giữa hai điểm \(M\) và \(P\), Điểm \(O\) nằm giữa hai điểm \(M\) và \(N\).
1. Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
*Điểm
Dấu chấm nhỏ là hình ảnh của điểm
Quy ước: Khi nói 2 điểm mà không nói gì thêm, ta hiểu đó là 2 điểm phân biệt
*Đường thẳng
Đường thẳng không bị giới hạn về 2 phía
*Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
Ta thường dùng chữ cái in hoa để đặt tên điểm và chữ cái thường để đặt tên đường thẳng, chẳng hạn điểm M,N,P,Q,...; đường thẳng a,b,d,...
Điểm A thuộc đường thẳng d, kí hiệu \(A \in d\)
Điểm B không đường thẳng d, kí hiệu là \(B \notin d\)
Nếu \(A \in d\), ta còn nói: Điểm A nằm trên đường thẳng d, hay đường thẳng d đi qua điểm A
Chú ý: Có vô số điểm thuộc đường thẳng
*Đường thẳng đi qua 2 điểm
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm A và B
Đường thẳng đi qua 2 điểm A, B được gọi đường thẳng AB hay đường thẳng BA
2. Điểm nằm giữa 2 điểm
+) Ba điểm phân biệt A, B, C cùng thuộc một đường thẳng được gọi là ba điểm thẳng hàng.
+) Ba điểm phân biệt D, E, F không cùng thuộc bất kì một đường thẳng nào được gọi là ba điểm không thẳng hàng.
Trong ba điểm thẳng hàng, có một điểm và chỉ một điểm nằm giữa hai điểm còn lại.
3 điểm A,B,C cùng nằm trên đường thẳng d như hình sau
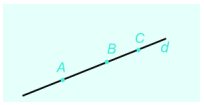
Điểm B nằm giữa 2 điểm A và C
2 điểm A và B nằm cùng phía đối với điểm C
2 điểm A và C nằm khác phía đối với điểm B
3. Tia
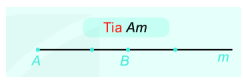
+ Tia Am gồm điểm A, điểm B và các điểm nằm cùng phía với B đối với A. Tia Am còn được kí hiệu là tia AB. Điểm A là điểm gốc của tia
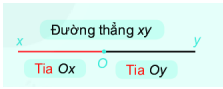
+ Điểm O nằm trên đường thẳng xy chia đường thẳng thành 2 phần. Mỗi phần đó cùng với điểm O làm thành một tia. Khi đó 2 tia Ox và Oy gọi là 2 tia đối nhau
Nhận xét:

- Nếu hai tia OA và OB đối nhau thì điểm \(O\) nằm giữa hai điểm \(A\) và \(B\)
- Ngược lại, nếu điểm \(O\) nằm giữa hai điểm \(A\) và \(B\) thì:
+ Hai tia OA;OB đối nhau
+ Hai tia AO;AB trùng nhau; hai tia BO;BA trùng nhau
Bài 1:
Cho hình vẽ:
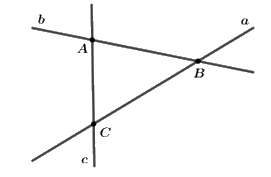
Đường thẳng nào không đi qua điểm \(A\)?
Bài 2:
Vẽ hình theo cách diễn đạt sau: Điểm \(E\) nằm trên đường thẳng \(x\) nhưng không nằm trên đường thẳng \(a\). Đường thẳng \(x\) đi qua điểm \(F\) nằm trên đường thẳng \(a\).
Bài 3:
Vẽ điểm \(C\) sao cho \(C\) thuộc đường thẳng \(xy\) và điểm \(C\) nằm giữa hai điểm \(A\) và \(B\). Kể tên các tia chung gốc \(A\) có trong hình vẽ.
Bài 4:
Cho bốn điểm \(O,M,N,P\) thỏa mãn điều kiện: Hai tia \(OM\) và \(ON\) là hai tia đối nhau, hai tia \(OM\) và \(OP\) là hai tia đối nhau.
a) Có nhận xét gì về bốn điểm \(M,N,O,P\)?
b) Điểm \(O\) nằm giữa hai điểm nào?
Lời giải chi tiết:
Bài 1:
Cho hình vẽ:
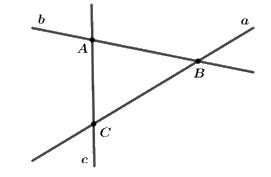
Đường thẳng nào không đi qua điểm \(A\)?
Phương pháp
Quan sát hình vẽ và tìm những đường thẳng cùng đi qua điểm \(A\).
Lời giải
Quan sát hình vẽ ta thấy: Điểm \(A\) nằm trên hai đường thẳng \(b\) và \(c\); Điểm \(A\) nằm ngoài đường thẳng \(a\).
Các đường thẳng đi qua điểm \(A\) là: Đường thẳng \(b\) và đường thẳng \(c\)
Đường thẳng \(a\) không đi qua điểm \(A\).
Bài 2:
Vẽ hình theo cách diễn đạt sau: Điểm \(E\) nằm trên đường thẳng \(x\) nhưng không nằm trên đường thẳng \(a\). Đường thẳng \(x\) đi qua điểm \(F\) nằm trên đường thẳng \(a\).
Phương pháp
+ Viết dưới dạng kí hiệu cách diễn đạt với bài bài.
+ Quan sát hình vẽ, tìm mỗi quan hệ của các điểm với từng đường thẳng.
Lời giải
Điểm \(E\) nằm trên đường thẳng \(x\) nhưng không nằm trên đường thẳng \(a\) nghĩa là: \(E \in x\) nhưng \(E \notin a\).
Đường thẳng \(x\) đi qua điểm \(F\) nằm trên đường thẳng \(a\) nghĩa là: \(F \in x\) và \(F \in a\).
Bài 3:
Vẽ điểm \(C\) sao cho \(C\) thuộc đường thẳng \(xy\) và điểm \(C\) nằm giữa hai điểm \(A\) và \(B\). Kể tên các tia chung gốc \(A\) có trong hình vẽ.
Phương pháp
Sử dụng định nghĩa hai tia đối nhau, định nghĩa về tia.
Lời giải
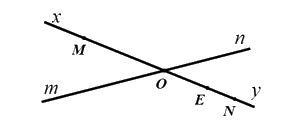
a) Các tia đối nhau trong hình vẽ là:\(Ox,Oy,Om,On\)
b) Ta có \(OM\) và \(Oy\) là hai tia đối nhau nên \(N \in Oy\) thì \(OM\) và \(ON\) là hai tia đối nhau.
Bài 4:
Cho bốn điểm \(O,M,N,P\) thỏa mãn điều kiện: Hai tia \(OM\) và \(ON\) là hai tia đối nhau, hai tia \(OM\) và \(OP\) là hai tia đối nhau.
a) Có nhận xét gì về bốn điểm \(M,N,O,P\)?
b) Điểm \(O\) nằm giữa hai điểm nào?
Phương pháp
Sử dụng khái niệm hai tia đối nhau, quan hệ giữa ba điểm thẳng hàng.
Lời giải
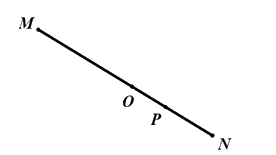
a) Ta có \(OM\) và \(ON\) là hai tia đối nhau nên ba điểm \(M,N,O\) cùng thuộc một đường thẳng,
Ta có \(OM\) và \(OP\) là hai tia đối nhau nên ba điểm \(M,O,P\) cùng thuộc một đường thẳng.
Suy ra bốn điểm \(M,N,O,P\) cùng thuộc một đường thẳng.
b) Điểm \(O\) nằm giữa hai điểm \(M\) và \(P\), Điểm \(O\) nằm giữa hai điểm \(M\) và \(N\).
Điểm và đường thẳng là những khái niệm cơ bản nhất trong hình học. Hiểu rõ về chúng là nền tảng để học tốt các kiến thức hình học phức tạp hơn. Trong chương trình Toán 6, việc nắm vững kiến thức về điểm và đường thẳng là vô cùng quan trọng, đặc biệt trong giai đoạn ôn hè để chuẩn bị cho năm học mới.
Có ba trường hợp xảy ra khi xét vị trí tương đối giữa một điểm và một đường thẳng:
Có một số loại đường thẳng thường gặp:
Bài 1: Vẽ đường thẳng a và các điểm M, N, P sao cho M nằm trên a, N nằm ngoài a, P trùng với a.
Bài 2: Cho ba điểm A, B, C không thẳng hàng. Vẽ đường thẳng đi qua hai điểm A và B. Điểm C có vị trí như thế nào so với đường thẳng AB?
Bài 3: Vẽ hai đường thẳng song song d1 và d2. Vẽ đường thẳng d3 cắt cả hai đường thẳng d1 và d2. Các góc tạo thành có tính chất gì?
Để hiểu sâu hơn về điểm và đường thẳng, các em có thể tìm hiểu thêm về:
Để học tốt dạng bài tập về điểm và đường thẳng, các em cần:
Hy vọng với bài học này, các em sẽ nắm vững kiến thức về Dạng 1: Điểm và Đường Thẳng - Chủ đề 10 Ôn hè Toán 6. Chúc các em học tập tốt!