Dạng 2 trong Chủ đề 8 Ôn hè Toán 6 tập trung vào việc rèn luyện kỹ năng tính chu vi và diện tích của các hình phẳng cơ bản. Đây là một phần kiến thức quan trọng, đặt nền móng cho các bài học hình học phức tạp hơn ở các lớp trên.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng, bài tập và phương pháp giải chi tiết, giúp học sinh nắm vững kiến thức và tự tin giải quyết các bài toán liên quan đến chu vi và diện tích.
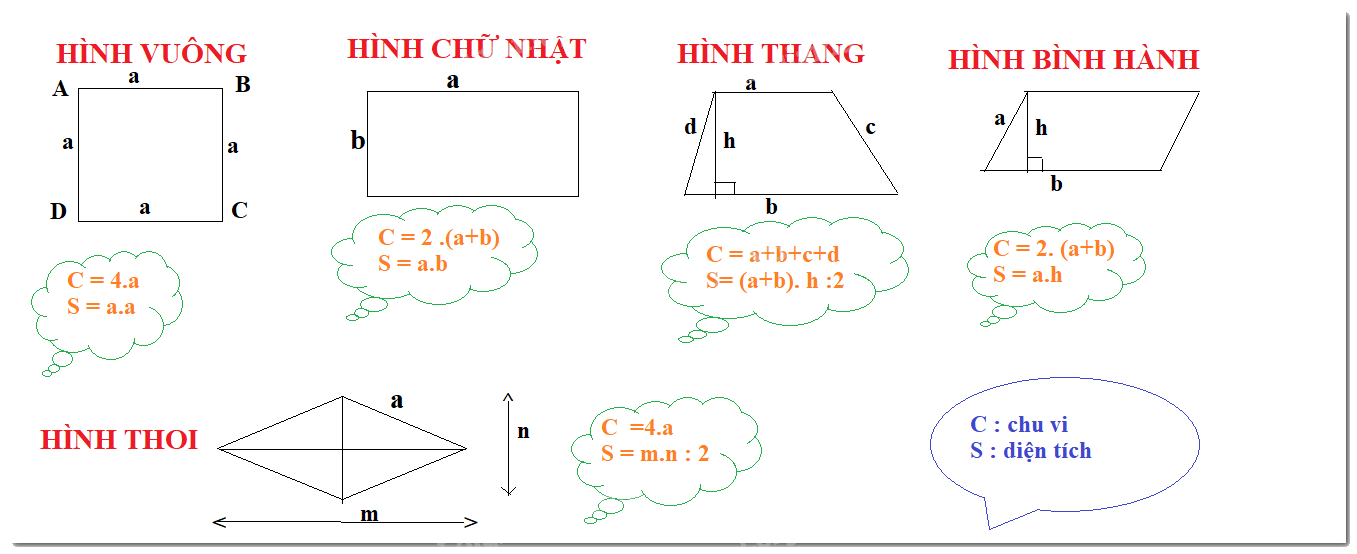
Công thức tính chu vi và diện tích:
Công thức tính chu vi và diện tích:
Bài 1:
Một mảnh đất hình chữ nhật có chiều dài là \(20m\) và chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Người ta muốn làm hàng rào xung quanh, ở giữa làm một hồ nuôi cá hình thoi và phần đất còn lại trồng hoa. Biết hồ nuôi cá có độ dài hai đường chéo là \(10,5m\) và \(16m\).
a) Tính chi phí vật liệu để người ta rào được xung quanh mảnh đất. Biết chi phí vật liệu để rào được \(1m\) là \(225\,\,000\) đồng.
b) Nếu một túi hạt giống có gieo vừa đủ trên \(24{m^2}\) đất thì cần bao nhiêu túi hạt giống để gieo hết mảnh vườn trồng hoa? Biết diện tích hàng rào không đáng kể.
Bài 2:
Tính diện tích hình sau:
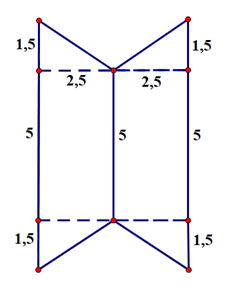
Bài 3:
Một thửa ruộng hình thang có đáy bé \(26m\), đáy lớn hơn đáy bé \(8m\), đáy bé hơn chiều cao \(6m\). Trung bình cứ \(100{m^2}\) thu hoạch được \(70,5kg\) thóc. Hỏi thu hoạch được bao nhiêu ki-lô-gam thóc trên thửa ruộng đó?
Bài 4:
Bác Hưng uốn một dây thép thành móc treo đồ có dạng hình thoi với độ dài cạnh bằng \(30cm\). Bác Hưng cần bao nhiêu xăng-ti-mét dây thép để làm móc treo đó?
Bài 5:
Một người dự định lát đá và trồng cỏ xen kẽ cho sân của một ngôi nhà. Sân có dạng hình chữ nhật kích thước \(20m \times 30m\). Người ta dùng \(1400\) viên đá lát hình vuông cạnh \(60cm\) để lát, diện tích còn lại dùng để trồng cỏ. Hỏi cần phải bỏ ra chi phí bao nhiêu để trồng cỏ, biết giá mỗi mét vuông cỏ là \(30000\) đồng?
Lời giải chi tiết:
Bài 1:
Một mảnh đất hình chữ nhật có chiều dài là \(20m\) và chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Người ta muốn làm hàng rào xung quanh, ở giữa làm một hồ nuôi cá hình thoi và phần đất còn lại trồng hoa. Biết hồ nuôi cá có độ dài hai đường chéo là \(10,5m\) và \(16m\).
a) Tính chi phí vật liệu để người ta rào được xung quanh mảnh đất. Biết chi phí vật liệu để rào được \(1m\) là \(225\,\,000\) đồng.
b) Nếu một túi hạt giống có gieo vừa đủ trên \(24{m^2}\) đất thì cần bao nhiêu túi hạt giống để gieo hết mảnh vườn trồng hoa? Biết diện tích hàng rào không đáng kể.
Phương pháp
a) + Tính chu vi mảnh đất.
+ Tính tổng chi phí vật liệu = Chu vi mảnh đất ´ Chi phí vật liệu rào \(1m\).
b) Tính diện tích mảnh đất.
+ Tính diện tích hồ nuôi cá.
+ Tính diện tích đất trồng hoa.
+ Tính số túi hạt giống = Diện tích đất trồng hoa : Diện tích đất 1 túi hạt giống gieo được
Lời giải
Chiều rộng mảnh đất là:
\(20.\dfrac{3}{4} = 15\left( m \right)\)
a) Chu vi mảnh đất là:
\(\left( {20 + 15} \right).2 = 70\left( m \right)\)
Chi phí vật liệu để người ta rào xung quanh mảnh đất là:
\(70.225\,\,000 = 15\,\,750\,\,000\) (đồng)
b) Diện tích mảnh đất là:
\(20.15 = 300\left( {{m^2}} \right)\)
Diện tích hồ nuôi cá là:
\(\dfrac{{10,5.16}}{2} = 84\left( {{m^2}} \right)\)
Diện tích đất trồng hoa là:
\(300 - 84 = 216\left( {{m^2}} \right)\)
Số túi hạt giống để giao hết mảnh vườn trồng hoa là:
\(216:24 = 9\)(túi)
Bài 2:
Tính diện tích hình sau:
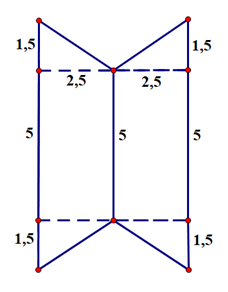
Phương pháp
+ Phân tích hình vẽ: Hình vẽ gồm hai hình thang bằng nhau.
+ Tính diện tích một hình thang.
+ Tính diện tích hình cần tìm = 2. Diện tích hình thang.
Lời giải
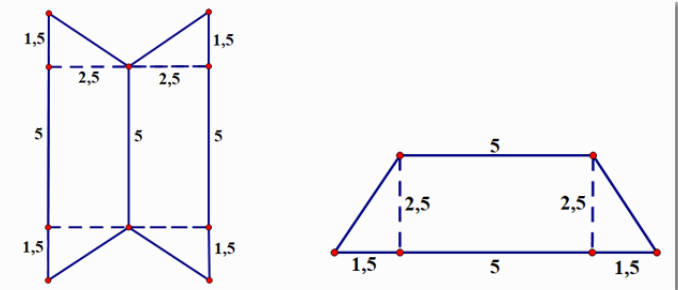
Độ dài đáy lớn của hình thang là:
\(1,5 + 5 + 1,5 = 8\)(đơn vị độ dài)
Diện tích hình thang là:
\(\dfrac{{\left( {5 + 8} \right).2,5}}{2} = 16,25\)(đơn vị diện tích)
Bài 3:
Một thửa ruộng hình thang có đáy bé \(26m\), đáy lớn hơn đáy bé \(8m\), đáy bé hơn chiều cao \(6m\). Trung bình cứ \(100{m^2}\) thu hoạch được \(70,5kg\) thóc. Hỏi thu hoạch được bao nhiêu ki-lô-gam thóc trên thửa ruộng đó?
Phương pháp
Tính diện tích thửa ruộng.
Tính số ki-lô-gam thóc thu hoạch được trên thửa ruộng.
Lời giải
Đáy lớn của thửa ruộng hình thang là:
\(26 + 8 = 34\,\,\left( m \right)\)
Chiều cao của thửa ruộng hình thang là:
\(26-6 = 20{\rm{ }}\left( m \right)\)
Diện tích thửa ruộng hình thang là:
\(\left( {34 + 26} \right).20:2 = 600\,\left( {{m^2}} \right)\)
\(600{m^2}\) gấp \(100{m^2}\) số lần là:
\(600:100 = 6\,\,\left( {{m^2}} \right)\)
Số ki-lô-gam thóc thu hoạch được trên thửa ruộng đó:
\(6.70,5 = 423\,\,\left( {kg} \right)\)
Bài 4:
Bác Hưng uốn một dây thép thành móc treo đồ có dạng hình thoi với độ dài cạnh bằng \(30cm\). Bác Hưng cần bao nhiêu xăng-ti-mét dây thép để làm móc treo đó?
Phương pháp
Sử dụng công thức tính chu vi hình thoi.
Lời giải
Độ dài dây thép để làm móc treo chính là chu vi của hình thoi có độ dài cạnh bằng \(30cm\).
Do đó bác Hưng cần số xăng-ti-mét dây thép để làm móc treo là:
\(30.4 = \,\,120\left( {cm} \right)\)
Vậy bác Hưng cần số xăng-ti-mét dây thép để làm móc treo là \(120cm\).
Bài 5:
Một người dự định lát đá và trồng cỏ xen kẽ cho sân của một ngôi nhà. Sân có dạng hình chữ nhật kích thước \(20m \times 30m\). Người ta dùng \(1400\) viên đá lát hình vuông cạnh \(60cm\) để lát, diện tích còn lại dùng để trồng cỏ. Hỏi cần phải bỏ ra chi phí bao nhiêu để trồng cỏ, biết giá mỗi mét vuông cỏ là \(30000\) đồng?
Phương pháp
Tính diện tích sân, viên đá lát hình vuông, diện tích phần đá lát sân, diện tích phần đất để trồng cỏ. Từ đó tính được chi phí bỏ ra để trồng cỏ.
Lời giải
Đổi: \(60cm = 0,6m\;\)
Diện tích sân là:
\(20.30 = 600\,\,\left( {{m^2}} \right)\)
Diện tích một viên đá lát hình vuông là:
\(0,6.0,6 = 0,36{\rm{ }}\left( {{m^2}} \right)\)
Diện tích phần đá lát sân là:
\(0,36.1400 = 504{\rm{ }}\left( {{m^2}} \right)\)
Diện tích phần đất để trồng cỏ là:
\(600--504 = 96{\rm{ }}\left( {{m^2}} \right)\)
Chi phí bỏ ra để trồng cỏ là:
\(96.30000 = 2\,880\,000\) (đồng)
Vậy chi phí bỏ ra để trồng cỏ là \(2\,880\,000\) đồng.
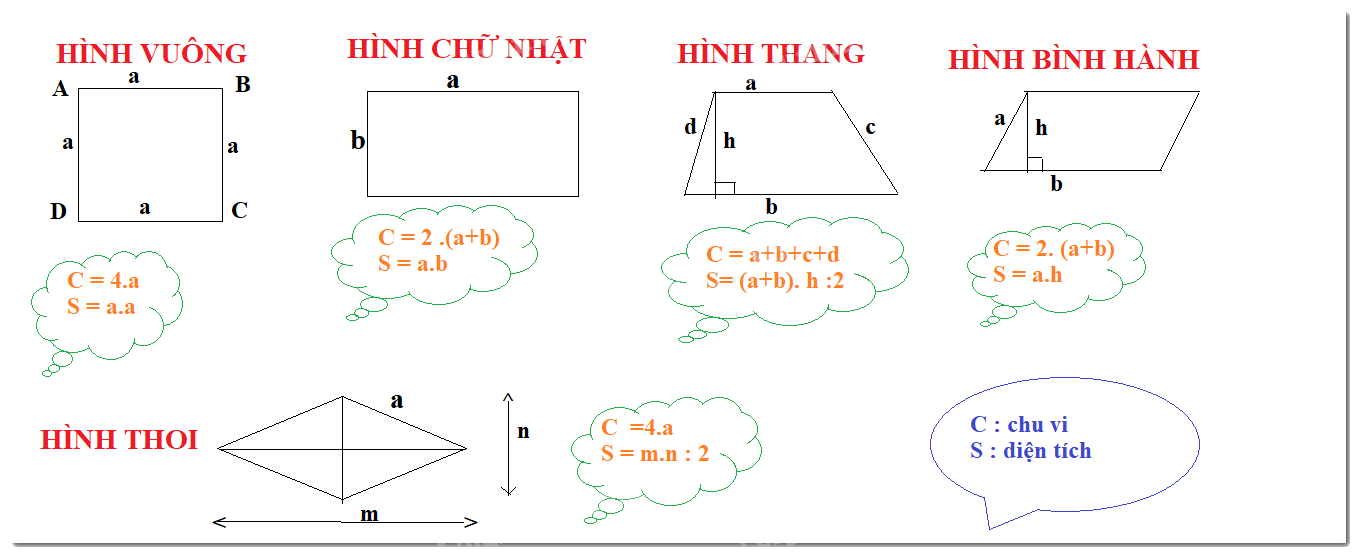
Công thức tính chu vi và diện tích:
Bài 1:
Một mảnh đất hình chữ nhật có chiều dài là \(20m\) và chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Người ta muốn làm hàng rào xung quanh, ở giữa làm một hồ nuôi cá hình thoi và phần đất còn lại trồng hoa. Biết hồ nuôi cá có độ dài hai đường chéo là \(10,5m\) và \(16m\).
a) Tính chi phí vật liệu để người ta rào được xung quanh mảnh đất. Biết chi phí vật liệu để rào được \(1m\) là \(225\,\,000\) đồng.
b) Nếu một túi hạt giống có gieo vừa đủ trên \(24{m^2}\) đất thì cần bao nhiêu túi hạt giống để gieo hết mảnh vườn trồng hoa? Biết diện tích hàng rào không đáng kể.
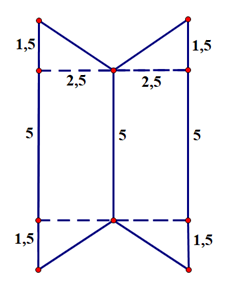
Bài 2:
Tính diện tích hình sau:
Bài 3:
Một thửa ruộng hình thang có đáy bé \(26m\), đáy lớn hơn đáy bé \(8m\), đáy bé hơn chiều cao \(6m\). Trung bình cứ \(100{m^2}\) thu hoạch được \(70,5kg\) thóc. Hỏi thu hoạch được bao nhiêu ki-lô-gam thóc trên thửa ruộng đó?
Bài 4:
Bác Hưng uốn một dây thép thành móc treo đồ có dạng hình thoi với độ dài cạnh bằng \(30cm\). Bác Hưng cần bao nhiêu xăng-ti-mét dây thép để làm móc treo đó?
Bài 5:
Một người dự định lát đá và trồng cỏ xen kẽ cho sân của một ngôi nhà. Sân có dạng hình chữ nhật kích thước \(20m \times 30m\). Người ta dùng \(1400\) viên đá lát hình vuông cạnh \(60cm\) để lát, diện tích còn lại dùng để trồng cỏ. Hỏi cần phải bỏ ra chi phí bao nhiêu để trồng cỏ, biết giá mỗi mét vuông cỏ là \(30000\) đồng?
Lời giải chi tiết:
Bài 1:
Một mảnh đất hình chữ nhật có chiều dài là \(20m\) và chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Người ta muốn làm hàng rào xung quanh, ở giữa làm một hồ nuôi cá hình thoi và phần đất còn lại trồng hoa. Biết hồ nuôi cá có độ dài hai đường chéo là \(10,5m\) và \(16m\).
a) Tính chi phí vật liệu để người ta rào được xung quanh mảnh đất. Biết chi phí vật liệu để rào được \(1m\) là \(225\,\,000\) đồng.
b) Nếu một túi hạt giống có gieo vừa đủ trên \(24{m^2}\) đất thì cần bao nhiêu túi hạt giống để gieo hết mảnh vườn trồng hoa? Biết diện tích hàng rào không đáng kể.
Phương pháp
a) + Tính chu vi mảnh đất.
+ Tính tổng chi phí vật liệu = Chu vi mảnh đất ´ Chi phí vật liệu rào \(1m\).
b) Tính diện tích mảnh đất.
+ Tính diện tích hồ nuôi cá.
+ Tính diện tích đất trồng hoa.
+ Tính số túi hạt giống = Diện tích đất trồng hoa : Diện tích đất 1 túi hạt giống gieo được
Lời giải
Chiều rộng mảnh đất là:
\(20.\dfrac{3}{4} = 15\left( m \right)\)
a) Chu vi mảnh đất là:
\(\left( {20 + 15} \right).2 = 70\left( m \right)\)
Chi phí vật liệu để người ta rào xung quanh mảnh đất là:
\(70.225\,\,000 = 15\,\,750\,\,000\) (đồng)
b) Diện tích mảnh đất là:
\(20.15 = 300\left( {{m^2}} \right)\)
Diện tích hồ nuôi cá là:
\(\dfrac{{10,5.16}}{2} = 84\left( {{m^2}} \right)\)
Diện tích đất trồng hoa là:
\(300 - 84 = 216\left( {{m^2}} \right)\)
Số túi hạt giống để giao hết mảnh vườn trồng hoa là:
\(216:24 = 9\)(túi)
Bài 2:
Tính diện tích hình sau:
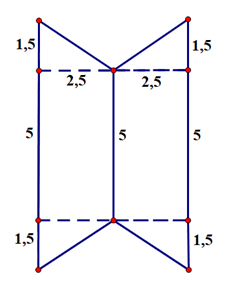
Phương pháp
+ Phân tích hình vẽ: Hình vẽ gồm hai hình thang bằng nhau.
+ Tính diện tích một hình thang.
+ Tính diện tích hình cần tìm = 2. Diện tích hình thang.
Lời giải
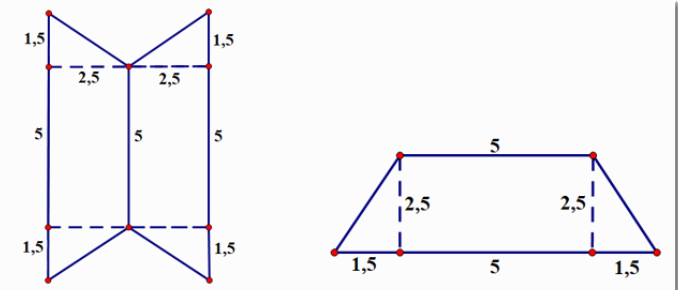
Độ dài đáy lớn của hình thang là:
\(1,5 + 5 + 1,5 = 8\)(đơn vị độ dài)
Diện tích hình thang là:
\(\dfrac{{\left( {5 + 8} \right).2,5}}{2} = 16,25\)(đơn vị diện tích)
Bài 3:
Một thửa ruộng hình thang có đáy bé \(26m\), đáy lớn hơn đáy bé \(8m\), đáy bé hơn chiều cao \(6m\). Trung bình cứ \(100{m^2}\) thu hoạch được \(70,5kg\) thóc. Hỏi thu hoạch được bao nhiêu ki-lô-gam thóc trên thửa ruộng đó?
Phương pháp
Tính diện tích thửa ruộng.
Tính số ki-lô-gam thóc thu hoạch được trên thửa ruộng.
Lời giải
Đáy lớn của thửa ruộng hình thang là:
\(26 + 8 = 34\,\,\left( m \right)\)
Chiều cao của thửa ruộng hình thang là:
\(26-6 = 20{\rm{ }}\left( m \right)\)
Diện tích thửa ruộng hình thang là:
\(\left( {34 + 26} \right).20:2 = 600\,\left( {{m^2}} \right)\)
\(600{m^2}\) gấp \(100{m^2}\) số lần là:
\(600:100 = 6\,\,\left( {{m^2}} \right)\)
Số ki-lô-gam thóc thu hoạch được trên thửa ruộng đó:
\(6.70,5 = 423\,\,\left( {kg} \right)\)
Bài 4:
Bác Hưng uốn một dây thép thành móc treo đồ có dạng hình thoi với độ dài cạnh bằng \(30cm\). Bác Hưng cần bao nhiêu xăng-ti-mét dây thép để làm móc treo đó?
Phương pháp
Sử dụng công thức tính chu vi hình thoi.
Lời giải
Độ dài dây thép để làm móc treo chính là chu vi của hình thoi có độ dài cạnh bằng \(30cm\).
Do đó bác Hưng cần số xăng-ti-mét dây thép để làm móc treo là:
\(30.4 = \,\,120\left( {cm} \right)\)
Vậy bác Hưng cần số xăng-ti-mét dây thép để làm móc treo là \(120cm\).
Bài 5:
Một người dự định lát đá và trồng cỏ xen kẽ cho sân của một ngôi nhà. Sân có dạng hình chữ nhật kích thước \(20m \times 30m\). Người ta dùng \(1400\) viên đá lát hình vuông cạnh \(60cm\) để lát, diện tích còn lại dùng để trồng cỏ. Hỏi cần phải bỏ ra chi phí bao nhiêu để trồng cỏ, biết giá mỗi mét vuông cỏ là \(30000\) đồng?
Phương pháp
Tính diện tích sân, viên đá lát hình vuông, diện tích phần đá lát sân, diện tích phần đất để trồng cỏ. Từ đó tính được chi phí bỏ ra để trồng cỏ.
Lời giải
Đổi: \(60cm = 0,6m\;\)
Diện tích sân là:
\(20.30 = 600\,\,\left( {{m^2}} \right)\)
Diện tích một viên đá lát hình vuông là:
\(0,6.0,6 = 0,36{\rm{ }}\left( {{m^2}} \right)\)
Diện tích phần đá lát sân là:
\(0,36.1400 = 504{\rm{ }}\left( {{m^2}} \right)\)
Diện tích phần đất để trồng cỏ là:
\(600--504 = 96{\rm{ }}\left( {{m^2}} \right)\)
Chi phí bỏ ra để trồng cỏ là:
\(96.30000 = 2\,880\,000\) (đồng)
Vậy chi phí bỏ ra để trồng cỏ là \(2\,880\,000\) đồng.
Chào mừng các em học sinh đến với bài học về Dạng 2: Tính chu vi và diện tích hình phẳng trong chương trình Ôn hè Toán 6. Đây là một trong những chủ đề quan trọng giúp các em củng cố kiến thức nền tảng về hình học, chuẩn bị cho năm học mới.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các khái niệm cơ bản sau:
Dưới đây là công thức tính chu vi và diện tích của một số hình phẳng thường gặp:
Để giải các bài tập về tính chu vi và diện tích hình phẳng, các em cần:
Bài 1: Một hình chữ nhật có chiều dài 8cm và chiều rộng 5cm. Tính chu vi và diện tích của hình chữ nhật đó.
Giải:
Bài 2: Một hình vuông có cạnh 6cm. Tính chu vi và diện tích của hình vuông đó.
Giải:
Để củng cố kiến thức, các em hãy tự giải thêm các bài tập sau:
Hy vọng bài học về Dạng 2: Tính chu vi và diện tích hình phẳng đã giúp các em hiểu rõ hơn về kiến thức này. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
Chúc các em học tốt!