Chào mừng bạn đến với bài kiểm tra trắc nghiệm về Bài 3: Đoạn thẳng trong chương trình Toán 6 Cánh diều. Bài trắc nghiệm này được thiết kế để giúp bạn củng cố kiến thức và đánh giá mức độ hiểu bài của mình.
Giaitoan.edu.vn cung cấp bộ câu hỏi đa dạng, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp bạn làm quen với nhiều dạng đề thi.
Kể tên các đoạn thẳng có trong hình vẽ dưới đây
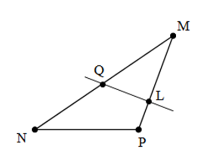
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
$MN;QL;MQ;NQ;ML;LP;MP$
$MN;\,MQ;NQ;ML;QL;MP;NP$
$MN;\,MQ;ML;MP;NP$
Cho G là một điểm thuộc đoạn thẳng HK ( G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm giữa hai điểm còn lại?
Điểm G
Điểm H
Điểm K
Không có điểm nào nằm giữa hai điểm còn lại.
Cho $10$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng, cứ qua hai điểm ta vẽ một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
$10$
$90$
$40$
$45$
Cho $n$ điểm phân biệt $\left( {n \ge 2;\,n \in N} \right)$ trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong $n$ điểm đó. Có tất cả $28$ đoạn thẳng. Hãy tìm $n.$
$n = 9.$
$n = 7.$
$n = 8.$
$n = 6.$
Đường thẳng \(xx'\) cắt bao nhiêu đoạn thẳng trên hình vẽ sau
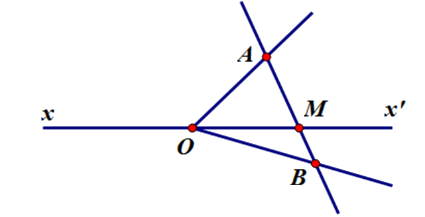
$3$
$4$
$5$
$6$
Cho các đoạn thẳng \(AB = 4cm;\,MN = 5cm;\,EF = 3\,cm;\,PQ = 4cm;\,IK = 5\,cm\). Chọn đáp án sai.
\(AB < MN\)
$EF < IK$
\(AB = PQ\)
\(AB = EF\)
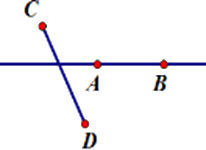
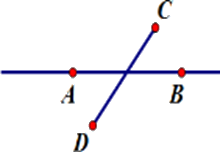
Hãy chọn hình vẽ đúng theo diễn đạt sau: Vẽ đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD.$
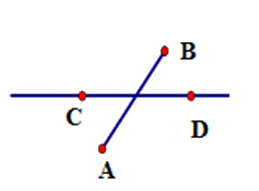
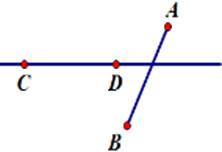
Cho $E$ là điểm nằm giữa hai điểm $I$ và $K.$ Biết rằng $IE = 4cm,EK = 10cm.$Tính độ dài đoạn thẳng $IK.$
$4cm$
$7cm$
$6cm$
$14cm$
Cho đoạn thẳng $IK = 8cm$. Điểm $P$ nằm giữa hai điểm $I$ và $K$ sao cho \(IP - PK = 4cm.\) Tính độ dài các đoạn thẳng $PI$ và $PK.$
\(IP = 2cm;PK = 6cm.\)
\(IP = 3cm;PK = 5cm.\)
\(IP = 6cm;PK = 2cm.\)
\(IP = 5cm;PK = 1cm.\)
Cho đoạn thẳng $AB = 4,5cm$ và điểm $C$ nằm giữa hai điểm $A$ và $B$. Biết $AC = \dfrac{2}{3}CB$. Tính độ dài đoạn thẳng $AC$ và $BC.$
$BC = 2,7cm;\,AC = 1,8cm.$
$BC = 1,8cm;\,AC = 2,7cm.$
$BC = 1,8cm;\,AC = 1,8cm.$
$BC = 2cm;\,AC = 3cm.$
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
$MA = MB$
\(AM = \dfrac{1}{2}AB\)
\(MA + MB = AB\)
$MA + MB = AB$ và $MA = MB$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
\(MP = NP = \dfrac{{MN}}{2}\)
\(MP + NP = 2MN\)
\(MP = NP = \dfrac{{MN}}{4}\)
\(MP = NP = MN\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
$3cm$
$15cm$
$6cm$
$20cm$
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
$4cm$
$16cm$
$21cm$
$24cm$
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
$1,5cm$
$3cm$
$4,5cm$
$6cm$
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
$8cm$
$4cm$
$2cm$
$6cm$
Lời giải và đáp án
Kể tên các đoạn thẳng có trong hình vẽ dưới đây
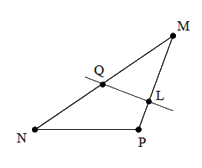
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
$MN;QL;MQ;NQ;ML;LP;MP$
$MN;\,MQ;NQ;ML;QL;MP;NP$
$MN;\,MQ;ML;MP;NP$
Đáp án : A
Sử dụng định nghĩa đoạn thẳng: “Đoạn thẳng \(AB\) là hình gồm điểm A, điểm B và tất cả các điểm nằm giữa A và B” để xác định các đoạn thẳng có trên hình vẽ.
Các đoạn thẳng có trên hình vẽ là:
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
Cho G là một điểm thuộc đoạn thẳng HK ( G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm giữa hai điểm còn lại?
Điểm G
Điểm H
Điểm K
Không có điểm nào nằm giữa hai điểm còn lại.
Đáp án : A
Dựa vào dấu hiệu nhận biết một điểm nằm giữa hai điểm.
“Nếu điểm $M$ thuộc đoạn thẳng $AB$ thì điểm $M$ nằm giữa hai điểm $A$ và $B$”
Vì G là một điểm thuộc đoạn thẳng HK nên G nằm giữa hai điểm H và K.
Cho $10$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng, cứ qua hai điểm ta vẽ một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
$10$
$90$
$40$
$45$
Đáp án : D
Sử dụng cách tính số đoạn thẳng:
Với \(n\) điểm cho trước \(\left( {n \in N;\,n \ge 2} \right)\) và không có ba điểm nào thẳng hàng thì số đoạn thẳng vẽ được là \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) .
Số đoạn thẳng cần tìm là
$\dfrac{{10.\left( {10 - 1} \right)}}{2} = 45$ đoạn thẳng
Cho $n$ điểm phân biệt $\left( {n \ge 2;\,n \in N} \right)$ trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong $n$ điểm đó. Có tất cả $28$ đoạn thẳng. Hãy tìm $n.$
$n = 9.$
$n = 7.$
$n = 8.$
$n = 6.$
Đáp án : C
Sử dụng công thức tính số đoạn thẳng:
Với \(n\) điểm cho trước \(\left( {n \in N;\,n \ge 2} \right)\) và không có ba điểm nào thẳng hàng thì số đoạn thẳng vẽ được là \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) .
Từ đó tìm ra $n.$
Số đoạn thẳng tạo thành từ $n$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng là $\dfrac{{n\left( {n - 1} \right)}}{2}$ $\left( {n \ge 2;\,n \in N} \right)$
Theo đề bài có $28$ đoạn thẳng được tạo thành nên ta có $\dfrac{{n\left( {n - 1} \right)}}{2} = 28 \Rightarrow n\left( {n - 1} \right) = 56 = 8.7$
Nhận thấy $\left( {n - 1} \right)$ và $n$ là hai số tự nhiên liên tiếp, suy ra $n = 8.$
Đường thẳng \(xx'\) cắt bao nhiêu đoạn thẳng trên hình vẽ sau
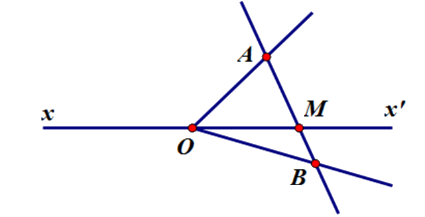
$3$
$4$
$5$
$6$
Đáp án : C
Sử dụng kiến thức về đường thẳng và đoạn thẳng cắt nhau:
“Nếu một đoạn thẳng chỉ có một điểm chung với đường thẳng thì chúng cắt nhau.”
Đường thẳng $xx'$ cắt năm đoạn thẳng $OA;OB;AB$; $MA;MB$
Cho các đoạn thẳng \(AB = 4cm;\,MN = 5cm;\,EF = 3\,cm;\,PQ = 4cm;\,IK = 5\,cm\). Chọn đáp án sai.
\(AB < MN\)
$EF < IK$
\(AB = PQ\)
\(AB = EF\)
Đáp án : D
Sử dụng kiến thức về so sánh hai đoạn thẳng
- Hai đoạn thẳng bằng nhau nếu có cùng độ dài.
- Đoạn thẳng lớn hơn nếu có độ dài lớn hơn.
+ Đáp án A: \(AB < MN\) là đúng vì $AB = 4cm < 5cm = MN$.
+ Đáp án B: $EF < IK$ là đúng vì $EF = 3cm < 5cm = IK$
+ Đáp án C: \(AB = PQ\) là đúng vì hai đoạn cùng có độ dài $4cm$
+ Đáp án D: \(AB = EF\) là sai vì $AB = 4cm > 3cm = EF$.
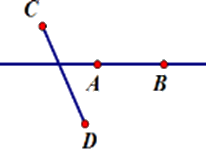
Hãy chọn hình vẽ đúng theo diễn đạt sau: Vẽ đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD.$
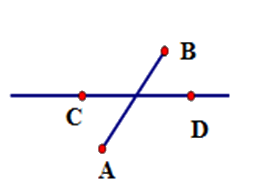
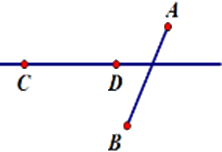
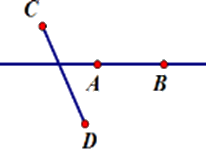
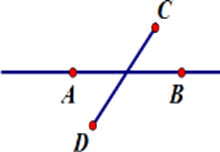
Đáp án : C
Sử dụng kiến thức:
Nếu một đoạn thẳng chỉ có một điểm chung với đường thẳng, tia hoặc đoạn thẳng khác thì chúng cắt nhau.
Đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD$ nghĩa là đoạn thẳng $AB$ không có điểm chung với đoạn thẳng $CD$ và đường thẳng $AB$có duy nhất một điểm chung với đoạn thẳng $CD.$
Hình vẽ thể hiện đúng diễn đạt trên là
Cho $E$ là điểm nằm giữa hai điểm $I$ và $K.$ Biết rằng $IE = 4cm,EK = 10cm.$Tính độ dài đoạn thẳng $IK.$
$4cm$
$7cm$
$6cm$
$14cm$
Đáp án : D
$E$ là điểm nằm giữa hai điểm $I$ và $K$ nên ta có công thức cộng đoạn thẳng $IE + EK = IK$. Biết độ dài $IL, LK$, thay số vào ta tính được độ dài đoạn thẳng $IK.$
Vì $E$ là điểm nằm giữa hai điểm $I$ và $K$ nên ta có $IE + EK = IK$
Hay $4 + 10 = IK$ suy ra $IK = 14\,cm.$
Cho đoạn thẳng $IK = 8cm$. Điểm $P$ nằm giữa hai điểm $I$ và $K$ sao cho \(IP - PK = 4cm.\) Tính độ dài các đoạn thẳng $PI$ và $PK.$
\(IP = 2cm;PK = 6cm.\)
\(IP = 3cm;PK = 5cm.\)
\(IP = 6cm;PK = 2cm.\)
\(IP = 5cm;PK = 1cm.\)
Đáp án : C
Sử dụng công thức cộng đoạn thẳng $PI + IK = PK$ và dữ kiện đề bài để tìm độ dài hai đoạn thẳng $PI;PK.$

Vì điểm $P$ nằm giữa hai điểm $I$ và $K$ nên ta có $PI + PK = IK \Rightarrow PI + IK = 8cm$ (1)
Theo đề bài \(IP - PK = 4cm\)(2)
Từ (1) và (2) suy ra \(IP = \dfrac{{8 + 4}}{2} = 6cm\) và \(PK = \dfrac{{8 - 4}}{2} = 2cm\)
Vậy \(IP = 6cm;PK = 2cm.\)
Cho đoạn thẳng $AB = 4,5cm$ và điểm $C$ nằm giữa hai điểm $A$ và $B$. Biết $AC = \dfrac{2}{3}CB$. Tính độ dài đoạn thẳng $AC$ và $BC.$
$BC = 2,7cm;\,AC = 1,8cm.$
$BC = 1,8cm;\,AC = 2,7cm.$
$BC = 1,8cm;\,AC = 1,8cm.$
$BC = 2cm;\,AC = 3cm.$
Đáp án : A
Sử dụng công thức cộng đoạn thẳng $AC + CB = AB$ và dữ kiện đề bài $AC = \dfrac{2}{3}CB$ để tính độ dài mỗi đoạn thẳng $AC$ và $BC.$
Vì điểm $C$ nằm giữa hai điểm $A$ và $B$ nên ta có $AC + CB = AB$ (1)
Thay $AC = \dfrac{2}{3}CB$ (theo đề bài) vào (1) ta được $\dfrac{2}{3}CB + CB = AB$ $ \Rightarrow CB.\left( {\dfrac{2}{3} + 1} \right) = 4,5$
$ \Rightarrow CB.\dfrac{5}{3} = \dfrac{9}{2}$$ \Rightarrow BC = \dfrac{9}{2}:\dfrac{5}{3} = \dfrac{{27}}{{10}} = 2,7\,cm$
Từ đó $AC = \dfrac{2}{3}BC = \dfrac{2}{3}.2,7 = 1,8cm$.
Vậy $BC = 2,7cm;\,AC = 1,8cm.$
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
$MA = MB$
\(AM = \dfrac{1}{2}AB\)
\(MA + MB = AB\)
$MA + MB = AB$ và $MA = MB$
Đáp án : D
\(M\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AM + MB = AB\\{\rm{MA = MB}}\end{array} \right.$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
\(MP = NP = \dfrac{{MN}}{2}\)
\(MP + NP = 2MN\)
\(MP = NP = \dfrac{{MN}}{4}\)
\(MP = NP = MN\)
Đáp án : A
Ta có \(P\) là trung điểm của \(MN\) thì \(MP = NP = \dfrac{{MN}}{2}\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
$3cm$
$15cm$
$6cm$
$20cm$
Đáp án : C
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$
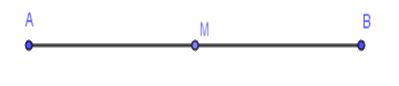
Vì \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = }}\dfrac{1}{2}AB = \dfrac{1}{2}.12 = 6cm$
Vậy $AM = 6cm$.
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
$4cm$
$16cm$
$21cm$
$24cm$
Đáp án : B
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$
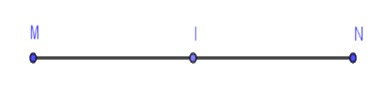
Vì $I$ là trung điểm của đoạn thẳng $MN$ nên $IM = IN = \dfrac{1}{2}MN$ hay $MN = 2.IN = 2.8 = 16cm$.
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
$1,5cm$
$3cm$
$4,5cm$
$6cm$
Đáp án : D
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.
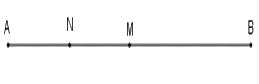
Vì $N$ là trung điểm đoạn $AM$ nên $AN = \dfrac{1}{2}AM$ hay $AM = 2AN = 2.1,5 = 3cm$
Lại có điểm $M$ là trung điểm đoạn thẳng $AB$ nên ta có $AM = \dfrac{1}{2}AB$ hay $AB = 2AM = 2.3 = 6cm$
Vậy $AB = 6cm$.
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
$8cm$
$4cm$
$2cm$
$6cm$
Đáp án : C
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.
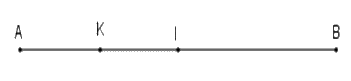
Vì điểm $I$ là trung điểm đoạn thẳng $AB$ nên $AI = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4cm$
Vì điểm $K$ là trung điểm đoạn thẳng $AI$ nên $AK = \dfrac{1}{2}AI = \dfrac{1}{2}.4 = 2cm$
Vậy $AI = 2cm$.
Kể tên các đoạn thẳng có trong hình vẽ dưới đây

$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
$MN;QL;MQ;NQ;ML;LP;MP$
$MN;\,MQ;NQ;ML;QL;MP;NP$
$MN;\,MQ;ML;MP;NP$
Cho G là một điểm thuộc đoạn thẳng HK ( G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm giữa hai điểm còn lại?
Điểm G
Điểm H
Điểm K
Không có điểm nào nằm giữa hai điểm còn lại.
Cho $10$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng, cứ qua hai điểm ta vẽ một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
$10$
$90$
$40$
$45$
Cho $n$ điểm phân biệt $\left( {n \ge 2;\,n \in N} \right)$ trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong $n$ điểm đó. Có tất cả $28$ đoạn thẳng. Hãy tìm $n.$
$n = 9.$
$n = 7.$
$n = 8.$
$n = 6.$
Đường thẳng \(xx'\) cắt bao nhiêu đoạn thẳng trên hình vẽ sau

$3$
$4$
$5$
$6$
Cho các đoạn thẳng \(AB = 4cm;\,MN = 5cm;\,EF = 3\,cm;\,PQ = 4cm;\,IK = 5\,cm\). Chọn đáp án sai.
\(AB < MN\)
$EF < IK$
\(AB = PQ\)
\(AB = EF\)
Hãy chọn hình vẽ đúng theo diễn đạt sau: Vẽ đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD.$




Cho $E$ là điểm nằm giữa hai điểm $I$ và $K.$ Biết rằng $IE = 4cm,EK = 10cm.$Tính độ dài đoạn thẳng $IK.$
$4cm$
$7cm$
$6cm$
$14cm$
Cho đoạn thẳng $IK = 8cm$. Điểm $P$ nằm giữa hai điểm $I$ và $K$ sao cho \(IP - PK = 4cm.\) Tính độ dài các đoạn thẳng $PI$ và $PK.$
\(IP = 2cm;PK = 6cm.\)
\(IP = 3cm;PK = 5cm.\)
\(IP = 6cm;PK = 2cm.\)
\(IP = 5cm;PK = 1cm.\)
Cho đoạn thẳng $AB = 4,5cm$ và điểm $C$ nằm giữa hai điểm $A$ và $B$. Biết $AC = \dfrac{2}{3}CB$. Tính độ dài đoạn thẳng $AC$ và $BC.$
$BC = 2,7cm;\,AC = 1,8cm.$
$BC = 1,8cm;\,AC = 2,7cm.$
$BC = 1,8cm;\,AC = 1,8cm.$
$BC = 2cm;\,AC = 3cm.$
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
$MA = MB$
\(AM = \dfrac{1}{2}AB\)
\(MA + MB = AB\)
$MA + MB = AB$ và $MA = MB$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
\(MP = NP = \dfrac{{MN}}{2}\)
\(MP + NP = 2MN\)
\(MP = NP = \dfrac{{MN}}{4}\)
\(MP = NP = MN\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
$3cm$
$15cm$
$6cm$
$20cm$
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
$4cm$
$16cm$
$21cm$
$24cm$
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
$1,5cm$
$3cm$
$4,5cm$
$6cm$
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
$8cm$
$4cm$
$2cm$
$6cm$
Kể tên các đoạn thẳng có trong hình vẽ dưới đây

$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
$MN;QL;MQ;NQ;ML;LP;MP$
$MN;\,MQ;NQ;ML;QL;MP;NP$
$MN;\,MQ;ML;MP;NP$
Đáp án : A
Sử dụng định nghĩa đoạn thẳng: “Đoạn thẳng \(AB\) là hình gồm điểm A, điểm B và tất cả các điểm nằm giữa A và B” để xác định các đoạn thẳng có trên hình vẽ.
Các đoạn thẳng có trên hình vẽ là:
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
Cho G là một điểm thuộc đoạn thẳng HK ( G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm giữa hai điểm còn lại?
Điểm G
Điểm H
Điểm K
Không có điểm nào nằm giữa hai điểm còn lại.
Đáp án : A
Dựa vào dấu hiệu nhận biết một điểm nằm giữa hai điểm.
“Nếu điểm $M$ thuộc đoạn thẳng $AB$ thì điểm $M$ nằm giữa hai điểm $A$ và $B$”
Vì G là một điểm thuộc đoạn thẳng HK nên G nằm giữa hai điểm H và K.
Cho $10$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng, cứ qua hai điểm ta vẽ một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
$10$
$90$
$40$
$45$
Đáp án : D
Sử dụng cách tính số đoạn thẳng:
Với \(n\) điểm cho trước \(\left( {n \in N;\,n \ge 2} \right)\) và không có ba điểm nào thẳng hàng thì số đoạn thẳng vẽ được là \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) .
Số đoạn thẳng cần tìm là
$\dfrac{{10.\left( {10 - 1} \right)}}{2} = 45$ đoạn thẳng
Cho $n$ điểm phân biệt $\left( {n \ge 2;\,n \in N} \right)$ trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong $n$ điểm đó. Có tất cả $28$ đoạn thẳng. Hãy tìm $n.$
$n = 9.$
$n = 7.$
$n = 8.$
$n = 6.$
Đáp án : C
Sử dụng công thức tính số đoạn thẳng:
Với \(n\) điểm cho trước \(\left( {n \in N;\,n \ge 2} \right)\) và không có ba điểm nào thẳng hàng thì số đoạn thẳng vẽ được là \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) .
Từ đó tìm ra $n.$
Số đoạn thẳng tạo thành từ $n$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng là $\dfrac{{n\left( {n - 1} \right)}}{2}$ $\left( {n \ge 2;\,n \in N} \right)$
Theo đề bài có $28$ đoạn thẳng được tạo thành nên ta có $\dfrac{{n\left( {n - 1} \right)}}{2} = 28 \Rightarrow n\left( {n - 1} \right) = 56 = 8.7$
Nhận thấy $\left( {n - 1} \right)$ và $n$ là hai số tự nhiên liên tiếp, suy ra $n = 8.$
Đường thẳng \(xx'\) cắt bao nhiêu đoạn thẳng trên hình vẽ sau

$3$
$4$
$5$
$6$
Đáp án : C
Sử dụng kiến thức về đường thẳng và đoạn thẳng cắt nhau:
“Nếu một đoạn thẳng chỉ có một điểm chung với đường thẳng thì chúng cắt nhau.”
Đường thẳng $xx'$ cắt năm đoạn thẳng $OA;OB;AB$; $MA;MB$
Cho các đoạn thẳng \(AB = 4cm;\,MN = 5cm;\,EF = 3\,cm;\,PQ = 4cm;\,IK = 5\,cm\). Chọn đáp án sai.
\(AB < MN\)
$EF < IK$
\(AB = PQ\)
\(AB = EF\)
Đáp án : D
Sử dụng kiến thức về so sánh hai đoạn thẳng
- Hai đoạn thẳng bằng nhau nếu có cùng độ dài.
- Đoạn thẳng lớn hơn nếu có độ dài lớn hơn.
+ Đáp án A: \(AB < MN\) là đúng vì $AB = 4cm < 5cm = MN$.
+ Đáp án B: $EF < IK$ là đúng vì $EF = 3cm < 5cm = IK$
+ Đáp án C: \(AB = PQ\) là đúng vì hai đoạn cùng có độ dài $4cm$
+ Đáp án D: \(AB = EF\) là sai vì $AB = 4cm > 3cm = EF$.
Hãy chọn hình vẽ đúng theo diễn đạt sau: Vẽ đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD.$




Đáp án : C
Sử dụng kiến thức:
Nếu một đoạn thẳng chỉ có một điểm chung với đường thẳng, tia hoặc đoạn thẳng khác thì chúng cắt nhau.
Đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD$ nghĩa là đoạn thẳng $AB$ không có điểm chung với đoạn thẳng $CD$ và đường thẳng $AB$có duy nhất một điểm chung với đoạn thẳng $CD.$
Hình vẽ thể hiện đúng diễn đạt trên là

Cho $E$ là điểm nằm giữa hai điểm $I$ và $K.$ Biết rằng $IE = 4cm,EK = 10cm.$Tính độ dài đoạn thẳng $IK.$
$4cm$
$7cm$
$6cm$
$14cm$
Đáp án : D
$E$ là điểm nằm giữa hai điểm $I$ và $K$ nên ta có công thức cộng đoạn thẳng $IE + EK = IK$. Biết độ dài $IL, LK$, thay số vào ta tính được độ dài đoạn thẳng $IK.$
Vì $E$ là điểm nằm giữa hai điểm $I$ và $K$ nên ta có $IE + EK = IK$
Hay $4 + 10 = IK$ suy ra $IK = 14\,cm.$
Cho đoạn thẳng $IK = 8cm$. Điểm $P$ nằm giữa hai điểm $I$ và $K$ sao cho \(IP - PK = 4cm.\) Tính độ dài các đoạn thẳng $PI$ và $PK.$
\(IP = 2cm;PK = 6cm.\)
\(IP = 3cm;PK = 5cm.\)
\(IP = 6cm;PK = 2cm.\)
\(IP = 5cm;PK = 1cm.\)
Đáp án : C
Sử dụng công thức cộng đoạn thẳng $PI + IK = PK$ và dữ kiện đề bài để tìm độ dài hai đoạn thẳng $PI;PK.$

Vì điểm $P$ nằm giữa hai điểm $I$ và $K$ nên ta có $PI + PK = IK \Rightarrow PI + IK = 8cm$ (1)
Theo đề bài \(IP - PK = 4cm\)(2)
Từ (1) và (2) suy ra \(IP = \dfrac{{8 + 4}}{2} = 6cm\) và \(PK = \dfrac{{8 - 4}}{2} = 2cm\)
Vậy \(IP = 6cm;PK = 2cm.\)
Cho đoạn thẳng $AB = 4,5cm$ và điểm $C$ nằm giữa hai điểm $A$ và $B$. Biết $AC = \dfrac{2}{3}CB$. Tính độ dài đoạn thẳng $AC$ và $BC.$
$BC = 2,7cm;\,AC = 1,8cm.$
$BC = 1,8cm;\,AC = 2,7cm.$
$BC = 1,8cm;\,AC = 1,8cm.$
$BC = 2cm;\,AC = 3cm.$
Đáp án : A
Sử dụng công thức cộng đoạn thẳng $AC + CB = AB$ và dữ kiện đề bài $AC = \dfrac{2}{3}CB$ để tính độ dài mỗi đoạn thẳng $AC$ và $BC.$
Vì điểm $C$ nằm giữa hai điểm $A$ và $B$ nên ta có $AC + CB = AB$ (1)
Thay $AC = \dfrac{2}{3}CB$ (theo đề bài) vào (1) ta được $\dfrac{2}{3}CB + CB = AB$ $ \Rightarrow CB.\left( {\dfrac{2}{3} + 1} \right) = 4,5$
$ \Rightarrow CB.\dfrac{5}{3} = \dfrac{9}{2}$$ \Rightarrow BC = \dfrac{9}{2}:\dfrac{5}{3} = \dfrac{{27}}{{10}} = 2,7\,cm$
Từ đó $AC = \dfrac{2}{3}BC = \dfrac{2}{3}.2,7 = 1,8cm$.
Vậy $BC = 2,7cm;\,AC = 1,8cm.$
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
$MA = MB$
\(AM = \dfrac{1}{2}AB\)
\(MA + MB = AB\)
$MA + MB = AB$ và $MA = MB$
Đáp án : D
\(M\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AM + MB = AB\\{\rm{MA = MB}}\end{array} \right.$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
\(MP = NP = \dfrac{{MN}}{2}\)
\(MP + NP = 2MN\)
\(MP = NP = \dfrac{{MN}}{4}\)
\(MP = NP = MN\)
Đáp án : A
Ta có \(P\) là trung điểm của \(MN\) thì \(MP = NP = \dfrac{{MN}}{2}\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
$3cm$
$15cm$
$6cm$
$20cm$
Đáp án : C
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$

Vì \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = }}\dfrac{1}{2}AB = \dfrac{1}{2}.12 = 6cm$
Vậy $AM = 6cm$.
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
$4cm$
$16cm$
$21cm$
$24cm$
Đáp án : B
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$

Vì $I$ là trung điểm của đoạn thẳng $MN$ nên $IM = IN = \dfrac{1}{2}MN$ hay $MN = 2.IN = 2.8 = 16cm$.
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
$1,5cm$
$3cm$
$4,5cm$
$6cm$
Đáp án : D
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.

Vì $N$ là trung điểm đoạn $AM$ nên $AN = \dfrac{1}{2}AM$ hay $AM = 2AN = 2.1,5 = 3cm$
Lại có điểm $M$ là trung điểm đoạn thẳng $AB$ nên ta có $AM = \dfrac{1}{2}AB$ hay $AB = 2AM = 2.3 = 6cm$
Vậy $AB = 6cm$.
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
$8cm$
$4cm$
$2cm$
$6cm$
Đáp án : C
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.

Vì điểm $I$ là trung điểm đoạn thẳng $AB$ nên $AI = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4cm$
Vì điểm $K$ là trung điểm đoạn thẳng $AI$ nên $AK = \dfrac{1}{2}AI = \dfrac{1}{2}.4 = 2cm$
Vậy $AI = 2cm$.
Bài 3: Đoạn thẳng trong chương trình Toán 6 Cánh diều là một phần quan trọng trong việc xây dựng nền tảng hình học cơ bản. Bài học này giới thiệu khái niệm về đoạn thẳng, các tính chất của đoạn thẳng, và cách đo độ dài đoạn thẳng. Việc nắm vững kiến thức này là cần thiết để giải quyết các bài toán hình học phức tạp hơn trong tương lai.
Để giải các bài tập trắc nghiệm về đoạn thẳng, bạn cần nắm vững các khái niệm cơ bản và các công thức liên quan. Hãy đọc kỹ đề bài, xác định các thông tin đã cho và yêu cầu của bài toán. Sau đó, áp dụng các kiến thức đã học để tìm ra đáp án chính xác.
Câu hỏi: Cho đoạn thẳng AB có độ dài 10cm. Gọi M là trung điểm của đoạn thẳng AB. Độ dài đoạn thẳng AM là bao nhiêu?
Giải: Vì M là trung điểm của đoạn thẳng AB, nên AM = MB = AB/2 = 10cm/2 = 5cm.
Đáp án: 5cm
Để nâng cao kỹ năng giải bài tập trắc nghiệm về đoạn thẳng, bạn nên luyện tập thêm với nhiều dạng bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp bạn rèn luyện và củng cố kiến thức một cách hiệu quả.
Việc học tốt Bài 3: Đoạn thẳng không chỉ giúp bạn đạt điểm cao trong các bài kiểm tra, mà còn là nền tảng quan trọng để bạn học tốt các bài học hình học tiếp theo. Hiểu rõ về đoạn thẳng, trung điểm, và độ dài đoạn thẳng sẽ giúp bạn giải quyết các bài toán phức tạp hơn một cách dễ dàng và hiệu quả.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về trắc nghiệm Bài 3: Đoạn thẳng Toán 6 Cánh diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất!