Chào mừng các em học sinh đến với bài kiểm tra trắc nghiệm Bài 1: Tam giác đều. Hình lục giác đều môn Toán 6, sách Cánh diều. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức đã học về các khái niệm cơ bản của tam giác đều và hình lục giác đều.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, kèm đáp án chi tiết và lời giải thích dễ hiểu, giúp các em tự tin hơn trong quá trình học tập.
Phát biểu nào sau đây sai?
Hình lục giác đều có 6 đỉnh
Hình lục giác đều có 6 cạnh
Hình lục giác đều có 6 đường chéo chính
Hình lục giác đều có 6 góc
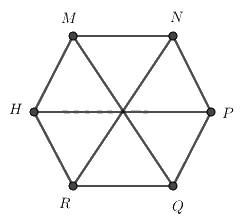
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
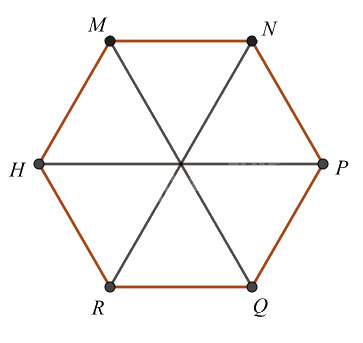
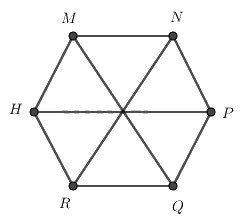
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Chọn phát biểu sai:
Tam giác đều có ba cạnh
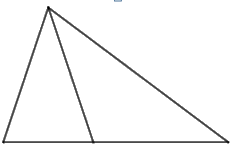
Hình dưới đây có mấy hình tam giác?
Hình lục giác đều có mấy cạnh
3
5
6
8
Cho lục giác đều \(ABCDEF\) có \(AB = 3cm\), chọn câu đúng
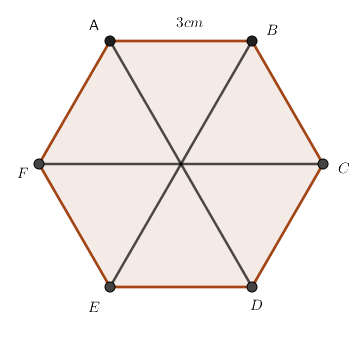
FC=3cm
AD= 3cm
BE= 3cm
EF=3cm
Hình lục giác đều có bao nhiêu đường chéo chính
1
2
3
4
Lời giải và đáp án
Phát biểu nào sau đây sai?
Hình lục giác đều có 6 đỉnh
Hình lục giác đều có 6 cạnh
Hình lục giác đều có 6 đường chéo chính
Hình lục giác đều có 6 góc
Đáp án : C
Sử dụng dấu hiệu nhận biết lục giác đều.
Các đáp án A, B, D đúng.
Hình lục giác đều có 3 đường chéo chính => Đáp án C sai.
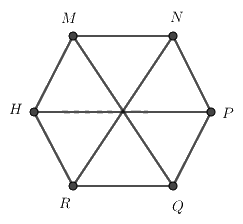
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : D
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: \(MQ = NR\)
=> A đúng
Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên \(MH = RQ\) và \(MN = HR\)
=> B, C đúng.
Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau
=> D sai
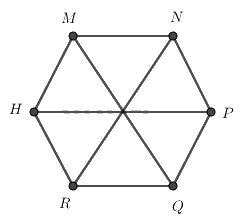
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
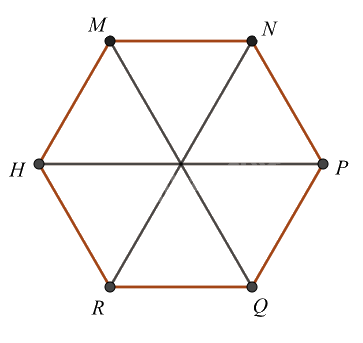
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
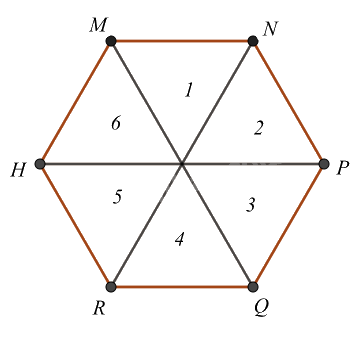
Ta đánh số như hình trên
Hình lục giác đều được tạo thành bởi 6 hình tam giác đều nên các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : B
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Đáp án B sai do MQ là đường chéo chính, sửa lại:
6 cạnh là MN, NP, PQ, HR, QR, HM
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Đáp án : D
Trong tam giác đều ba cạnh bằng nhau mà \(MN = 5\,cm\) nên ta có: \(MN = NP = MP = 5\,cm\)
=> Chọn D
Chọn phát biểu sai:
Tam giác đều có ba cạnh
Đáp án : C
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Hình dưới đây có mấy hình tam giác?
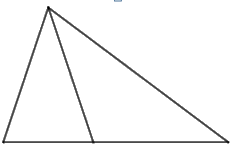
Đáp án : C
Đếm số hình tam giác nhỏ + số hình tam giác tạo từ các hình tam giác nhỏ
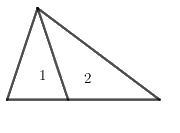
Hình trên có 2 hình tam giác nhỏ là: 1, 2 và 1 hình tam giác lớn ghép từ hai hình trên
=> Có tất cả 3 hình tam giác
Hình lục giác đều có mấy cạnh
3
5
6
8
Đáp án : C
Hình lục giác đều có 6 cạnh
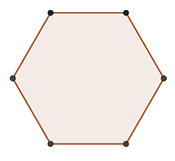
Cho lục giác đều \(ABCDEF\) có \(AB = 3cm\), chọn câu đúng
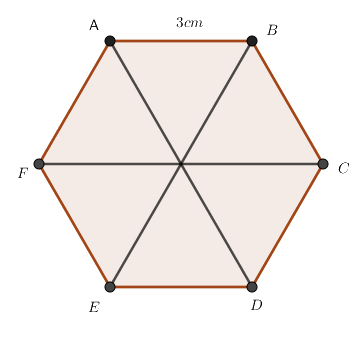
FC=3cm
AD= 3cm
BE= 3cm
EF=3cm
Đáp án : D
Lục giác đều có các cạnh bằng nhau nên AB=EF=3cm
Các đoạn thẳng AD, BE, FC là các đường chéo chính nên không bằng cạnh bên.
Hình lục giác đều có bao nhiêu đường chéo chính
1
2
3
4
Đáp án : C
Hình lục giác đều có 3 đường chéo chính
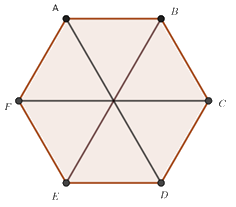
Ví dụ: Lục giác đều ABCD có các đường chéo chính là: AD, BE, FC
Phát biểu nào sau đây sai?
Hình lục giác đều có 6 đỉnh
Hình lục giác đều có 6 cạnh
Hình lục giác đều có 6 đường chéo chính
Hình lục giác đều có 6 góc

Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều


Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Chọn phát biểu sai:
Tam giác đều có ba cạnh
Hình dưới đây có mấy hình tam giác?

Hình lục giác đều có mấy cạnh
3
5
6
8
Cho lục giác đều \(ABCDEF\) có \(AB = 3cm\), chọn câu đúng

FC=3cm
AD= 3cm
BE= 3cm
EF=3cm
Hình lục giác đều có bao nhiêu đường chéo chính
1
2
3
4
Phát biểu nào sau đây sai?
Hình lục giác đều có 6 đỉnh
Hình lục giác đều có 6 cạnh
Hình lục giác đều có 6 đường chéo chính
Hình lục giác đều có 6 góc
Đáp án : C
Sử dụng dấu hiệu nhận biết lục giác đều.
Các đáp án A, B, D đúng.
Hình lục giác đều có 3 đường chéo chính => Đáp án C sai.

Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : D
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: \(MQ = NR\)
=> A đúng
Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên \(MH = RQ\) và \(MN = HR\)
=> B, C đúng.
Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau
=> D sai
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

Ta đánh số như hình trên
Hình lục giác đều được tạo thành bởi 6 hình tam giác đều nên các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.

Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : B
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Đáp án B sai do MQ là đường chéo chính, sửa lại:
6 cạnh là MN, NP, PQ, HR, QR, HM
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Đáp án : D
Trong tam giác đều ba cạnh bằng nhau mà \(MN = 5\,cm\) nên ta có: \(MN = NP = MP = 5\,cm\)
=> Chọn D
Chọn phát biểu sai:
Tam giác đều có ba cạnh
Đáp án : C
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Hình dưới đây có mấy hình tam giác?

Đáp án : C
Đếm số hình tam giác nhỏ + số hình tam giác tạo từ các hình tam giác nhỏ

Hình trên có 2 hình tam giác nhỏ là: 1, 2 và 1 hình tam giác lớn ghép từ hai hình trên
=> Có tất cả 3 hình tam giác
Hình lục giác đều có mấy cạnh
3
5
6
8
Đáp án : C
Hình lục giác đều có 6 cạnh

Cho lục giác đều \(ABCDEF\) có \(AB = 3cm\), chọn câu đúng

FC=3cm
AD= 3cm
BE= 3cm
EF=3cm
Đáp án : D
Lục giác đều có các cạnh bằng nhau nên AB=EF=3cm
Các đoạn thẳng AD, BE, FC là các đường chéo chính nên không bằng cạnh bên.
Hình lục giác đều có bao nhiêu đường chéo chính
1
2
3
4
Đáp án : C
Hình lục giác đều có 3 đường chéo chính

Ví dụ: Lục giác đều ABCD có các đường chéo chính là: AD, BE, FC
Bài 1 trong chương trình Toán 6 Cánh diều tập trung vào việc giới thiệu và làm quen với hai hình học cơ bản: tam giác đều và hình lục giác đều. Việc nắm vững các tính chất và cách nhận biết hai hình này là nền tảng quan trọng cho các bài học tiếp theo.
Tam giác đều là một loại tam giác đặc biệt, trong đó cả ba cạnh có độ dài bằng nhau. Từ đó, ba góc của tam giác đều cũng bằng nhau và có số đo là 60 độ. Để xác định một tam giác là tam giác đều, chúng ta cần chứng minh một trong các điều kiện sau:
Các tính chất quan trọng của tam giác đều bao gồm:
Hình lục giác đều là một đa giác có sáu cạnh bằng nhau và sáu góc bằng nhau. Mỗi góc của hình lục giác đều có số đo là 120 độ. Hình lục giác đều có thể được chia thành sáu tam giác đều bằng nhau, với tâm của hình lục giác là giao điểm của các đường chéo.
Để xác định một hình là hình lục giác đều, chúng ta cần chứng minh:
Các tính chất quan trọng của hình lục giác đều:
Dưới đây là một số câu hỏi trắc nghiệm minh họa để giúp các em làm quen với dạng bài tập này:
Đáp án: B
Đáp án: C
Đáp án: C
Để nắm vững kiến thức về tam giác đều và hình lục giác đều, các em nên thực hành giải nhiều bài tập trắc nghiệm khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú, được phân loại theo mức độ khó, giúp các em tự đánh giá năng lực và cải thiện kết quả học tập.
Tam giác đều và hình lục giác đều xuất hiện rất nhiều trong thực tế, ví dụ như:
Việc hiểu rõ về hai hình này không chỉ giúp các em giải quyết các bài toán trong sách giáo khoa mà còn ứng dụng vào cuộc sống hàng ngày.
Bài 1: Tam giác đều. Hình lục giác đều Toán 6 Cánh diều là một bài học quan trọng, đặt nền móng cho các kiến thức hình học tiếp theo. Hãy dành thời gian ôn tập kỹ lưỡng và luyện tập thường xuyên để đạt kết quả tốt nhất!