Chào mừng các em học sinh lớp 6 đến với chuyên mục trắc nghiệm Toán 6 của giaitoan.edu.vn.
Chuyên mục này cung cấp các bài trắc nghiệm đa dạng, bao gồm nhiều dạng bài tập khác nhau về tập hợp các số nguyên, bám sát chương trình Toán 6 Cánh diều.
Mục tiêu của chúng tôi là giúp các em ôn luyện kiến thức, rèn luyện kỹ năng giải bài tập và tự tin hơn trong các kỳ thi.
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
$3$
$ - 3$
$ - 4$
$4$
Những điểm cách điểm \(0\) ba đơn vị là
$3$ và \( - 3\)
$2$ và \( - 2\)
$2$ và \( - 3\)
$3$ và \( - 2\)
Những điểm cách điểm 3 năm đơn vị là:
$7$ và \( - 1\)
$6$ và \( - 2\)
$2$ và \( - 2\)
$8$ và \( - 2\)
Các số nguyên âm nằm giữa \( - 3\) và \(2\) là:
\( - 2; - 1\)
\( - 2; - 1;0;1\)
\( - 3; - 2; - 1;0;1;2\)
$0;1$
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
$3$
$5$
$6$
$7$
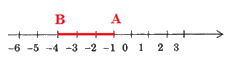
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
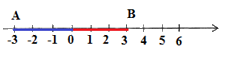
Cách viết nào sau đây là đúng:

Cho trục số:
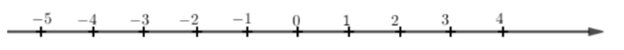
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?
Lời giải và đáp án
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
$3$
$ - 3$
$ - 4$
$4$
Đáp án : C
- Sử dụng trục số để tìm đáp án
+ Trên trục số: Điểm \(0\) được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.
Điểm cách $ - 1$ ba đơn vị theo chiều âm là điểm nằm phía bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị.
Điểm nằm bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị là điểm $ - 4$ Nên điểm cách $ - 1$ ba đơn vị theo chiều âm là $ - 4.$
Những điểm cách điểm \(0\) ba đơn vị là
$3$ và \( - 3\)
$2$ và \( - 2\)
$2$ và \( - 3\)
$3$ và \( - 2\)
Đáp án : A
Những điểm cách điểm $0$ ba đơn vị là điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị, điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị.
Điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị là: $3$ Điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị là: $ - 3$.
Những điểm cách điểm 3 năm đơn vị là:
$7$ và \( - 1\)
$6$ và \( - 2\)
$2$ và \( - 2\)
$8$ và \( - 2\)
Đáp án : D
Những điểm cách điểm $3$ năm đơn vị là điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị, điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị.
Điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị là: $8$ Điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị là: $ - 2$
Các số nguyên âm nằm giữa \( - 3\) và \(2\) là:
\( - 2; - 1\)
\( - 2; - 1;0;1\)
\( - 3; - 2; - 1;0;1;2\)
$0;1$
Đáp án : A
+ Các số nằm giữa $ - 3$ và $2$ là các số nằm bên phải $ - 3$ và bên trái của $2$ trên trục số.
+ Chọn các số nguyên âm trong các số vừa tìm được

Các số nguyên nằm giữa $ - 3$ và $2$ là: \( - 2; - 1;0;1.\)
Các số nguyên âm nằm giữa $ - 3$ và $2$ là: \( - 2; - 1.\)
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
$3$
$5$
$6$
$7$
Đáp án : C
Các số nằm giữa $ - 3$ và $4$ là các số nằm bên phải $ - 3$ và bên trái của $4$ trên trục số.

Các số nằm giữa $ - 3$ và $4$ là: \( - 2; - 1;0;1;2;3.\)
Vậy có \(6\) số thỏa mãn điều kiện đề bài.
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Đáp án : B
Dựa vào trục số để xác định.Lưu ý: Gốc trên trục tọa độ là điểm $0.$
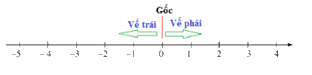
Quan sát trục số ta thấy:Điểm cách gốc $4$ đơn vị vế phía bên trái là điểm $ - 4,$ nên điểm A biểu diễn số: $ - 4$Điểm cách gốc $1$ đơn vị về phía bên phải là: $1$, nên điểm B biểu diễn số $1.$
Điểm $ - 4$ cách điểm $1$ là năm đơn vị.
Vậy điểm A cách điểm B là $5$ đơn vị.
Cách viết nào sau đây là đúng:
Đáp án : C
\(\begin{array}{l}\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,...} \right\}\\\mathbb{Z} = \left\{ {...;\, - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\end{array}\)
\( - 2\) không là số tự nhiên => Asai.
\(1,5\) và \(1\dfrac{1}{2}\) không là số nguyên => B, Dsai.
\( - 31\) là số nguyên => Cđúng.

Đáp án : B
Cho trục số:
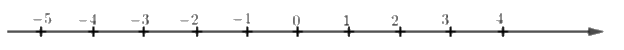
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Đáp án : C
Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.
Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.
Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?
Đáp án : B
Đáp án : D
Số đối của số \(a\) là \( - a\).
Số đối của số \( - a\) là \(a\).
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
$3$
$ - 3$
$ - 4$
$4$
Những điểm cách điểm \(0\) ba đơn vị là
$3$ và \( - 3\)
$2$ và \( - 2\)
$2$ và \( - 3\)
$3$ và \( - 2\)
Những điểm cách điểm 3 năm đơn vị là:
$7$ và \( - 1\)
$6$ và \( - 2\)
$2$ và \( - 2\)
$8$ và \( - 2\)
Các số nguyên âm nằm giữa \( - 3\) và \(2\) là:
\( - 2; - 1\)
\( - 2; - 1;0;1\)
\( - 3; - 2; - 1;0;1;2\)
$0;1$
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
$3$
$5$
$6$
$7$
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Cách viết nào sau đây là đúng:

Cho trục số:
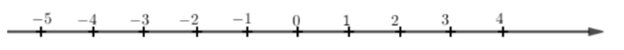
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
$3$
$ - 3$
$ - 4$
$4$
Đáp án : C
- Sử dụng trục số để tìm đáp án
+ Trên trục số: Điểm \(0\) được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.
Điểm cách $ - 1$ ba đơn vị theo chiều âm là điểm nằm phía bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị.

Điểm nằm bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị là điểm $ - 4$ Nên điểm cách $ - 1$ ba đơn vị theo chiều âm là $ - 4.$
Những điểm cách điểm \(0\) ba đơn vị là
$3$ và \( - 3\)
$2$ và \( - 2\)
$2$ và \( - 3\)
$3$ và \( - 2\)
Đáp án : A
Những điểm cách điểm $0$ ba đơn vị là điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị, điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị.

Điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị là: $3$ Điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị là: $ - 3$.
Những điểm cách điểm 3 năm đơn vị là:
$7$ và \( - 1\)
$6$ và \( - 2\)
$2$ và \( - 2\)
$8$ và \( - 2\)
Đáp án : D
Những điểm cách điểm $3$ năm đơn vị là điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị, điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị.
Điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị là: $8$ Điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị là: $ - 2$
Các số nguyên âm nằm giữa \( - 3\) và \(2\) là:
\( - 2; - 1\)
\( - 2; - 1;0;1\)
\( - 3; - 2; - 1;0;1;2\)
$0;1$
Đáp án : A
+ Các số nằm giữa $ - 3$ và $2$ là các số nằm bên phải $ - 3$ và bên trái của $2$ trên trục số.
+ Chọn các số nguyên âm trong các số vừa tìm được

Các số nguyên nằm giữa $ - 3$ và $2$ là: \( - 2; - 1;0;1.\)
Các số nguyên âm nằm giữa $ - 3$ và $2$ là: \( - 2; - 1.\)
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
$3$
$5$
$6$
$7$
Đáp án : C
Các số nằm giữa $ - 3$ và $4$ là các số nằm bên phải $ - 3$ và bên trái của $4$ trên trục số.

Các số nằm giữa $ - 3$ và $4$ là: \( - 2; - 1;0;1;2;3.\)
Vậy có \(6\) số thỏa mãn điều kiện đề bài.
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Đáp án : B
Dựa vào trục số để xác định.Lưu ý: Gốc trên trục tọa độ là điểm $0.$

Quan sát trục số ta thấy:Điểm cách gốc $4$ đơn vị vế phía bên trái là điểm $ - 4,$ nên điểm A biểu diễn số: $ - 4$Điểm cách gốc $1$ đơn vị về phía bên phải là: $1$, nên điểm B biểu diễn số $1.$
Điểm $ - 4$ cách điểm $1$ là năm đơn vị.
Vậy điểm A cách điểm B là $5$ đơn vị.
Cách viết nào sau đây là đúng:
Đáp án : C
\(\begin{array}{l}\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,...} \right\}\\\mathbb{Z} = \left\{ {...;\, - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\end{array}\)
\( - 2\) không là số tự nhiên => Asai.
\(1,5\) và \(1\dfrac{1}{2}\) không là số nguyên => B, Dsai.
\( - 31\) là số nguyên => Cđúng.

Đáp án : B
Cho trục số:
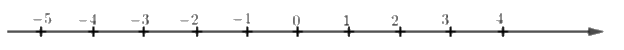
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Đáp án : C
Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.
Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.
Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?
Đáp án : B
Đáp án : D
Số đối của số \(a\) là \( - a\).
Số đối của số \( - a\) là \(a\).
Chương trình Toán 6 Cánh diều, phần tập hợp các số nguyên, là nền tảng quan trọng để học sinh làm quen với các khái niệm số học cơ bản. Việc nắm vững kiến thức về số nguyên âm, số nguyên dương, số 0, và các phép toán trên chúng là vô cùng cần thiết. Để giúp các em học sinh ôn tập và đánh giá kiến thức một cách hiệu quả, giaitoan.edu.vn xin giới thiệu bộ trắc nghiệm các dạng toán về tập hợp các số nguyên Toán 6 Cánh diều.
Để so sánh hai số nguyên, ta có thể sử dụng các quy tắc sau:
Ví dụ: So sánh -3 và 2. Ta có -3 < 2 vì -3 là số nguyên âm và 2 là số nguyên dương.
Để thực hiện phép cộng, trừ số nguyên, ta có thể sử dụng các quy tắc sau:
Ví dụ: Tính -5 + 3. Ta có -5 + 3 = -2 vì hai số nguyên khác dấu, ta lấy 5 - 3 = 2 và giữ dấu âm.
Hy vọng bộ trắc nghiệm các dạng toán về tập hợp các số nguyên Toán 6 Cánh diều của giaitoan.edu.vn sẽ giúp các em học sinh ôn tập kiến thức và đạt kết quả tốt trong các kỳ thi. Chúc các em học tập tốt!