Chào mừng các em học sinh đến với bài trắc nghiệm Bài 4: Phép nhân, phép chia các số tự nhiên môn Toán lớp 6, sách Cánh diều. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức đã học về phép nhân và phép chia các số tự nhiên.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, kèm đáp án chi tiết và lời giải dễ hiểu, giúp các em tự tin làm bài và đạt kết quả tốt nhất.
6+6+6+6 bằng
\(789 \times 123\) bằng:
97047
79047
47097
77047
Tích \(4 \times a \times b \times c\) bằng
\(4\)
\(4ab\)
\(4 + abc\)
\(4abc\)
Cho \(a,b,c\) là các số tự nhiên tùy ý. Khẳng định nào sau đây sai?
\(abc = \left( {ab} \right)c\)
\(abc = a\left( {bc} \right)\)
\(abc = b\left( {ac} \right)\)
\(abc = a + b + c\)
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
\(x\)
\(6\)
\(3\)
\(18\)
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\)duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng?
\(r \ge b\)
\(0 < b < r\)
\(0 < r < b\)
\(0 \le r < b\)
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
\(445 = 13.34 + 3\)
\(445 = 13.3 + 34\)
\(445 = 34.3 + 13\)
\(445 = 13.34\)
Trong các phép chia sau, có bao nhiêu phép chia có dư?
144:3
144:13
144:33
144:30
Tổng \(1 + 2 + 3 + 4 + ... + 2018\) bằng
\(4074342\)
\(2037171\)
\(2036162\)
\(2035152\)
Kết quả của phép tính \(\left( {158.129 - 158.39} \right):180\) có chữ số tận cùng là
\(8\)
\(79\)
\(9\)
\(5\)
Chọn kết luận đúng về số tự nhiên \(x\) thỏa mãn \(5x - 46:23 = 18.\)
\(x\) là số chẵn
\(x\) là số lẻ
\(x\) là số có hai chữ số
\(x = 0\)
Lời giải và đáp án
6+6+6+6 bằng
Đáp án : C
Đếm số các số 6 trong tổng.
Sử dụng kết quả: \(a.b = a + a + ... + a\) (Có b số hạng)
Kí hiệu của phép nhân là \(a \times b\) hoặc \(a.b\)
Tổng trên có 4 số 6 nên 6+6+6+6=6.4
\(789 \times 123\) bằng:
97047
79047
47097
77047
Đáp án : A
Đặt tính rồi tính.
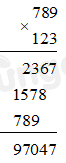
Vậy \(789 \times 123 = 97047\)
Tích \(4 \times a \times b \times c\) bằng
\(4\)
\(4ab\)
\(4 + abc\)
\(4abc\)
Đáp án : D
Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không viết dấu nhân giữa các thừa số.
\(4 \times a \times b \times c\) là tích của 4 thừa số:
Thừa số thứ nhất là một số: 4
Thừa số thứ 2, thứ 3, thứ 4 lần lượt là các chữ a,b,c.
Vậy tích này chỉ có 1 thừa số bằng số nên ta có thể bỏ dấu “\( \times \)” giữa các thừa số đi, tức là
\(4 \times a \times b \times c = 4abc\)
Cho \(a,b,c\) là các số tự nhiên tùy ý. Khẳng định nào sau đây sai?
\(abc = \left( {ab} \right)c\)
\(abc = a\left( {bc} \right)\)
\(abc = b\left( {ac} \right)\)
\(abc = a + b + c\)
Đáp án : D
Tích \(\left( {ab} \right)c\) hay \(a\left( {bc} \right)\) gọi là tích cả ba số a, b, c và viết gọn là \(abc\).
Tính chất giao hoán: \(a.b = b.a\)
\(\begin{array}{l}\left( {ab} \right)c = \left( {a.b} \right).c = a.b.c = abc\\a\left( {bc} \right) = a.\left( {b.c} \right) = a.b.c = abc\\b\left( {ac} \right) = b.\left( {a.c} \right) = b.a.c = a.b.c = abc\end{array}\)
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
\(x\)
\(6\)
\(3\)
\(18\)
Đáp án : B
Ta sử dụng (số bị chia) : (số chia) = (thương) để xác định thương của phép chia
Phép chia \(x:3 = 6\) có \(x\) là số bị chia; \(3\) là số chia và \(6\) là thương.
Nên thương của phép chia là \(6.\)
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\)duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng?
\(r \ge b\)
\(0 < b < r\)
\(0 < r < b\)
\(0 \le r < b\)
Đáp án : C
Định nghĩa về phép chia hết và phép chia có dư.
Khi chia a cho b, trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\)duy nhất sao cho:
\(a = b.q + r\)trong đó \(0 \le r < b\)
Phép chia a cho b là phép chia có dư nên \(r \ne 0\)
Vậy \(0 < r < b\).
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
\(445 = 13.34 + 3\)
\(445 = 13.3 + 34\)
\(445 = 34.3 + 13\)
\(445 = 13.34\)
Đáp án : A
Đặt tính rồi tính.
Xác định a,b,q,r trong phép chia vừa nhận được.
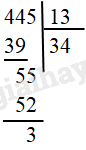
Số bị chia là \(b = 445\), số chia là \(b = 13\) thương \(q = 34\), số dư là \(r = 3\). Ta biểu diễn phép chia như sau: \(445 = 13.34 + 3\)
Trong các phép chia sau, có bao nhiêu phép chia có dư?
144:3
144:13
144:33
144:30
Đáp án : C
Đặt tính rồi tính.
Đếm số các phép chia có dư.
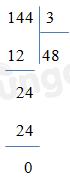
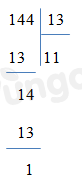
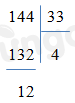
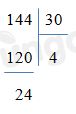
Vậy có 3 phép chia có dư
Tổng \(1 + 2 + 3 + 4 + ... + 2018\) bằng
\(4074342\)
\(2037171\)
\(2036162\)
\(2035152\)
Đáp án : B
+ Tính số các số tự nhiên liên tiếp từ \(1\) đến \(2018\) bằng công thức (số cuối-số đầu)+1
+ Tổng các số tự nhiên liên tiếp từ \(1\) đến \(2018\) được tính bằng công thức
(số cuối+số đầu). số các số hạng :2
Số các số tự nhiên liên tiếp từ \(1\) đến \(2018\) là \(2018 - 1 + 1 = 2018\) số
Như vậy từ \(1\) đến \(2018\) có số các số hạng là $2018.$
Tổng \(1 + 2 + 3 + 4 + ... + 2018\)\( = \left( {2018 + 1} \right).2018:2 = 2037171.\)
Kết quả của phép tính \(\left( {158.129 - 158.39} \right):180\) có chữ số tận cùng là
\(8\)
\(79\)
\(9\)
\(5\)
Đáp án : C
- Tính trong ngoặc bằng cách sử dụng \(ab - ac = a.\left( {b - c} \right).\)
- Thực hiện phép chia để tìm kết quả.
Ta có:
\(\left( {158.129 - 158.39} \right):180\)
\( = 158.\left( {129 - 39} \right):180 = 158.90:180\)
\( = 79.2.90:180 = 79.180:180 = 79.\)
Vậy kết quả của phép tính có chữ số tận cùng là \(9.\)
Chọn kết luận đúng về số tự nhiên \(x\) thỏa mãn \(5x - 46:23 = 18.\)
\(x\) là số chẵn
\(x\) là số lẻ
\(x\) là số có hai chữ số
\(x = 0\)
Đáp án : A
+ Thực hiện phép chia trước
+ Tìm số bị trừ bằng cách lấy hiệu cộng với số trừ
+ Tìm số hạng chưa biết bằng cách lấy tích chia cho số hạng đã biết
Ta có \(5x - 46:23 = 18\)
\(5x - 2 = 18\)
\(5x = 18 + 2\)
\(5x = 20\)
\(x = 20:5\)
\(x = 4\)
Vậy \(x = 4.\)
Do đó \(x\) là số chẵn.
6+6+6+6 bằng
\(789 \times 123\) bằng:
97047
79047
47097
77047
Tích \(4 \times a \times b \times c\) bằng
\(4\)
\(4ab\)
\(4 + abc\)
\(4abc\)
Cho \(a,b,c\) là các số tự nhiên tùy ý. Khẳng định nào sau đây sai?
\(abc = \left( {ab} \right)c\)
\(abc = a\left( {bc} \right)\)
\(abc = b\left( {ac} \right)\)
\(abc = a + b + c\)
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
\(x\)
\(6\)
\(3\)
\(18\)
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\)duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng?
\(r \ge b\)
\(0 < b < r\)
\(0 < r < b\)
\(0 \le r < b\)
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
\(445 = 13.34 + 3\)
\(445 = 13.3 + 34\)
\(445 = 34.3 + 13\)
\(445 = 13.34\)
Trong các phép chia sau, có bao nhiêu phép chia có dư?
144:3
144:13
144:33
144:30
Tổng \(1 + 2 + 3 + 4 + ... + 2018\) bằng
\(4074342\)
\(2037171\)
\(2036162\)
\(2035152\)
Kết quả của phép tính \(\left( {158.129 - 158.39} \right):180\) có chữ số tận cùng là
\(8\)
\(79\)
\(9\)
\(5\)
Chọn kết luận đúng về số tự nhiên \(x\) thỏa mãn \(5x - 46:23 = 18.\)
\(x\) là số chẵn
\(x\) là số lẻ
\(x\) là số có hai chữ số
\(x = 0\)
6+6+6+6 bằng
Đáp án : C
Đếm số các số 6 trong tổng.
Sử dụng kết quả: \(a.b = a + a + ... + a\) (Có b số hạng)
Kí hiệu của phép nhân là \(a \times b\) hoặc \(a.b\)
Tổng trên có 4 số 6 nên 6+6+6+6=6.4
\(789 \times 123\) bằng:
97047
79047
47097
77047
Đáp án : A
Đặt tính rồi tính.
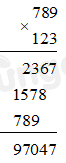
Vậy \(789 \times 123 = 97047\)
Tích \(4 \times a \times b \times c\) bằng
\(4\)
\(4ab\)
\(4 + abc\)
\(4abc\)
Đáp án : D
Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không viết dấu nhân giữa các thừa số.
\(4 \times a \times b \times c\) là tích của 4 thừa số:
Thừa số thứ nhất là một số: 4
Thừa số thứ 2, thứ 3, thứ 4 lần lượt là các chữ a,b,c.
Vậy tích này chỉ có 1 thừa số bằng số nên ta có thể bỏ dấu “\( \times \)” giữa các thừa số đi, tức là
\(4 \times a \times b \times c = 4abc\)
Cho \(a,b,c\) là các số tự nhiên tùy ý. Khẳng định nào sau đây sai?
\(abc = \left( {ab} \right)c\)
\(abc = a\left( {bc} \right)\)
\(abc = b\left( {ac} \right)\)
\(abc = a + b + c\)
Đáp án : D
Tích \(\left( {ab} \right)c\) hay \(a\left( {bc} \right)\) gọi là tích cả ba số a, b, c và viết gọn là \(abc\).
Tính chất giao hoán: \(a.b = b.a\)
\(\begin{array}{l}\left( {ab} \right)c = \left( {a.b} \right).c = a.b.c = abc\\a\left( {bc} \right) = a.\left( {b.c} \right) = a.b.c = abc\\b\left( {ac} \right) = b.\left( {a.c} \right) = b.a.c = a.b.c = abc\end{array}\)
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
\(x\)
\(6\)
\(3\)
\(18\)
Đáp án : B
Ta sử dụng (số bị chia) : (số chia) = (thương) để xác định thương của phép chia
Phép chia \(x:3 = 6\) có \(x\) là số bị chia; \(3\) là số chia và \(6\) là thương.
Nên thương của phép chia là \(6.\)
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\)duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng?
\(r \ge b\)
\(0 < b < r\)
\(0 < r < b\)
\(0 \le r < b\)
Đáp án : C
Định nghĩa về phép chia hết và phép chia có dư.
Khi chia a cho b, trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\)duy nhất sao cho:
\(a = b.q + r\)trong đó \(0 \le r < b\)
Phép chia a cho b là phép chia có dư nên \(r \ne 0\)
Vậy \(0 < r < b\).
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
\(445 = 13.34 + 3\)
\(445 = 13.3 + 34\)
\(445 = 34.3 + 13\)
\(445 = 13.34\)
Đáp án : A
Đặt tính rồi tính.
Xác định a,b,q,r trong phép chia vừa nhận được.
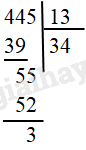
Số bị chia là \(b = 445\), số chia là \(b = 13\) thương \(q = 34\), số dư là \(r = 3\). Ta biểu diễn phép chia như sau: \(445 = 13.34 + 3\)
Trong các phép chia sau, có bao nhiêu phép chia có dư?
144:3
144:13
144:33
144:30
Đáp án : C
Đặt tính rồi tính.
Đếm số các phép chia có dư.
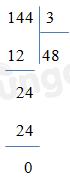
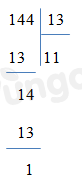
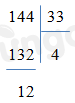
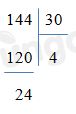
Vậy có 3 phép chia có dư
Tổng \(1 + 2 + 3 + 4 + ... + 2018\) bằng
\(4074342\)
\(2037171\)
\(2036162\)
\(2035152\)
Đáp án : B
+ Tính số các số tự nhiên liên tiếp từ \(1\) đến \(2018\) bằng công thức (số cuối-số đầu)+1
+ Tổng các số tự nhiên liên tiếp từ \(1\) đến \(2018\) được tính bằng công thức
(số cuối+số đầu). số các số hạng :2
Số các số tự nhiên liên tiếp từ \(1\) đến \(2018\) là \(2018 - 1 + 1 = 2018\) số
Như vậy từ \(1\) đến \(2018\) có số các số hạng là $2018.$
Tổng \(1 + 2 + 3 + 4 + ... + 2018\)\( = \left( {2018 + 1} \right).2018:2 = 2037171.\)
Kết quả của phép tính \(\left( {158.129 - 158.39} \right):180\) có chữ số tận cùng là
\(8\)
\(79\)
\(9\)
\(5\)
Đáp án : C
- Tính trong ngoặc bằng cách sử dụng \(ab - ac = a.\left( {b - c} \right).\)
- Thực hiện phép chia để tìm kết quả.
Ta có:
\(\left( {158.129 - 158.39} \right):180\)
\( = 158.\left( {129 - 39} \right):180 = 158.90:180\)
\( = 79.2.90:180 = 79.180:180 = 79.\)
Vậy kết quả của phép tính có chữ số tận cùng là \(9.\)
Chọn kết luận đúng về số tự nhiên \(x\) thỏa mãn \(5x - 46:23 = 18.\)
\(x\) là số chẵn
\(x\) là số lẻ
\(x\) là số có hai chữ số
\(x = 0\)
Đáp án : A
+ Thực hiện phép chia trước
+ Tìm số bị trừ bằng cách lấy hiệu cộng với số trừ
+ Tìm số hạng chưa biết bằng cách lấy tích chia cho số hạng đã biết
Ta có \(5x - 46:23 = 18\)
\(5x - 2 = 18\)
\(5x = 18 + 2\)
\(5x = 20\)
\(x = 20:5\)
\(x = 4\)
Vậy \(x = 4.\)
Do đó \(x\) là số chẵn.
Bài 4 trong chương trình Toán 6 Cánh diều tập trung vào việc củng cố kiến thức về phép nhân và phép chia các số tự nhiên. Đây là những phép tính cơ bản nhưng vô cùng quan trọng, là nền tảng cho các kiến thức toán học nâng cao hơn. Việc nắm vững các quy tắc, tính chất và kỹ năng thực hiện các phép tính này là điều cần thiết để học tốt môn Toán.
Bài học này bao gồm các nội dung chính sau:
Trong bài kiểm tra hoặc đề thi, các em thường gặp các dạng bài tập trắc nghiệm sau:
Để giải tốt các bài tập trắc nghiệm về phép nhân và phép chia các số tự nhiên, các em cần:
Câu 1: Tính 12 x 5 = ?
A. 50
B. 60
C. 70
D. 80
Đáp án: B. 60
Câu 2: Tìm số tự nhiên x sao cho x : 8 = 7
A. 48
B. 56
C. 64
D. 72
Đáp án: B. 56
Luyện tập trắc nghiệm không chỉ giúp các em củng cố kiến thức mà còn mang lại nhiều lợi ích khác:
Trắc nghiệm Bài 4: Phép nhân, phép chia các số tự nhiên Toán 6 Cánh diều là một phần quan trọng trong chương trình học Toán 6. Việc luyện tập thường xuyên và nắm vững kiến thức lý thuyết là chìa khóa để các em đạt kết quả tốt trong các bài kiểm tra và đề thi. Chúc các em học tốt!