Bài tập trắc nghiệm Bài 5: Góc Toán 6 Cánh diều là công cụ hỗ trợ học sinh ôn luyện và kiểm tra kiến thức về góc, các loại góc (góc nhọn, góc vuông, góc tù, góc bẹt) và cách đo góc. Giaitoan.edu.vn cung cấp bộ đề thi trắc nghiệm đa dạng, bám sát chương trình học, giúp các em tự tin hơn trong các bài kiểm tra.
Với giao diện thân thiện, dễ sử dụng, cùng đáp án và lời giải chi tiết, các em có thể tự học tại nhà hoặc sử dụng như một công cụ hỗ trợ trong quá trình học tập tại trường.
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Chọn câu sai.
Góc vuông là góc có số đo bằng \(90^\circ \)
Góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) là góc nhọn
Góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \)
Góc có số đo nhỏ hơn \(180^\circ \) là góc tù
Chọn phát biểu đúng.
Góc có số đo \(120^\circ \) là góc vuông
Góc có số đo \(80^\circ \) là góc tù
Góc có số đo \(100^\circ \) là góc nhọn
Góc có số đo \(150^\circ \) là góc tù
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Góc trên hình có số đo bao nhiêu độ

\(50^\circ \)
\(40^\circ \)
\(60^\circ \)
\(130^\circ \)
Cho hình vẽ sau
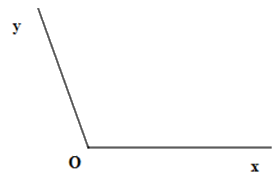
Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ
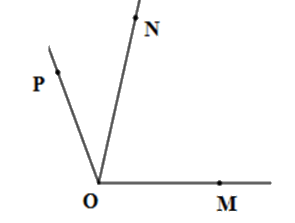
\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau
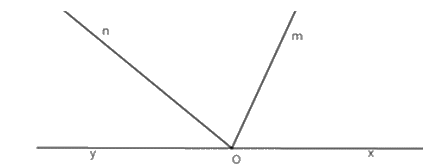
\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Cho \(\widehat {xOm} = 45^\circ \) và góc \(xOm\) bằng góc \(yAn\). Khi đó số đo góc \(yAn\) bằng
\(50^\circ \)
\(40^\circ \)
\(45^\circ \)
\(30^\circ \)
Cho các góc sau \(\widehat A = 30^\circ ;\,\widehat B = 60^\circ ;\,\widehat C = 110^\circ ;\widehat D = 90^\circ \). Chọn câu sai.
\(\widehat B < \widehat D\)
\(\widehat C < \widehat D\)
\(\widehat A < \widehat B\)
\(\widehat B < \widehat C\)
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Lời giải và đáp án
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Đáp án : B
Sử dụng kiến thức về góc và so sánh hai góc
Để so sánh hai góc ta so sánh số đo của chúng
Ta có:
+ Góc là hình gồm hai tia chung gốc nên A đúng
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau
+ Hai góc bằng nhau có số đo bằng nhau nên C đúng
+ Hai góc có số đo bằng nhau thì bằng nhau nên D đúng
Chọn câu sai.
Góc vuông là góc có số đo bằng \(90^\circ \)
Góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) là góc nhọn
Góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \)
Góc có số đo nhỏ hơn \(180^\circ \) là góc tù
Đáp án : D
Ta có góc vuông là góc có số đo bằng \(90^\circ \); Góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) là góc nhọn
và góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \) nên A, B, C đều đúng.
Góc có số đo nhỏ hơn \(180^\circ \) là góc tù là sai vì góc nhọn, góc vuông đều có số đo nhỏ hơn \(180^\circ .\)
Chọn phát biểu đúng.
Góc có số đo \(120^\circ \) là góc vuông
Góc có số đo \(80^\circ \) là góc tù
Góc có số đo \(100^\circ \) là góc nhọn
Góc có số đo \(150^\circ \) là góc tù
Đáp án : D
Ta sử dụng các kiến thức:
Góc vuông là góc có số đo bằng \(90^\circ \);
Góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) là góc nhọn
Góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \)
+ Vì \(90^\circ < 120^\circ < 180^\circ \) nên góc có số đo \(120^\circ \) là góc tù, do đó A sai
+ Vì \(0^\circ < 80^\circ < 90^\circ \) nên góc có số đo \(80^\circ \) là góc nhọn, do đó B sai
+ Vì \(90^\circ < 100^\circ < 180^\circ \) nên góc có số đo \(100^\circ \) là góc tù, do đó C sai
+ Vì \(90^\circ < 150^\circ < 180^\circ \) nên góc có số đo \(150^\circ \) là góc tù, do đó D đúng
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Đáp án : C
Ta sử dụng kiến thức:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Số góc tạo thành là \(\dfrac{{9.\left( {9 - 1} \right)}}{2} = 36\) góc.
Góc trên hình có số đo bao nhiêu độ

\(50^\circ \)
\(40^\circ \)
\(60^\circ \)
\(130^\circ \)
Đáp án : A
Quan sát số chỉ giá trị ở vòng trong thước đo độ
Góc trên hình có số đo \(50^\circ .\)
Cho hình vẽ sau
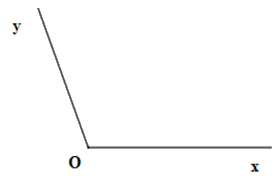
Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Đáp án : A
Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc.
Góc trên hình là góc \(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ
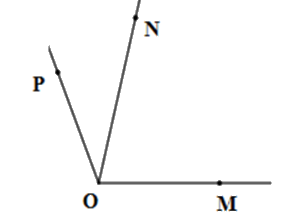
\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Đáp án : B
Quan sát hình vẽ, xác định các tia phân biệt chung gốc \(O\) từ đó tìm các góc tạo thành.
Các góc tạo thành là: \(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau
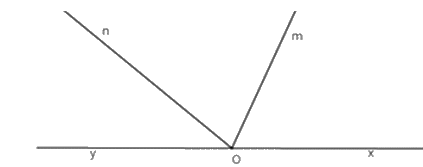
\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Đáp án : D
Xác định các tia chung gốc \(O\) từ đó xác định các góc có một cạnh là \(Om.\)
Các góc cần tìm là \(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\) .
Cho \(\widehat {xOm} = 45^\circ \) và góc \(xOm\) bằng góc \(yAn\). Khi đó số đo góc \(yAn\) bằng
\(50^\circ \)
\(40^\circ \)
\(45^\circ \)
\(30^\circ \)
Đáp án : C
Sử dụng: Hai góc bằng nhau có số đo bằng nhau
Vì \(\widehat {xOm} = \widehat {yAn}\) mà \(\widehat {xOm} = 45^\circ \) nên \(\widehat {yAn} = 45^\circ .\)
Cho các góc sau \(\widehat A = 30^\circ ;\,\widehat B = 60^\circ ;\,\widehat C = 110^\circ ;\widehat D = 90^\circ \). Chọn câu sai.
\(\widehat B < \widehat D\)
\(\widehat C < \widehat D\)
\(\widehat A < \widehat B\)
\(\widehat B < \widehat C\)
Đáp án : B
Trong hai góc: Góc nào có số đo lớn hơn thì góc đó lớn hơn.
Ta có
+) \(60^\circ < 90^\circ \) nên \(\widehat B < \widehat D\) suy ra A đúng.
+) \(110^\circ > 90^\circ \) nên \(\widehat C > \widehat D\) suy ra B sai
+) \(30^\circ < 60^\circ \) nên \(\widehat A < \widehat B\) suy ra C đúng.
+) \(60^\circ < 110^\circ \) nên \(\widehat B < \widehat C\) suy ra D đúng.
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Đáp án : B
Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt.
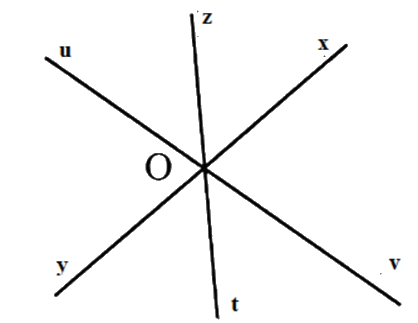
Các tia \(Ox\) và \(Oy;\) \(Oz\) và \(Ot;Ou\) và \(Ov\) là hai tia đối nhau nên các góc bẹt có đỉnh \(O\) tạo thành là
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\) .
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Đáp án : A
Sử dụng:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Từ đó tìm ra \(n.\)
Từ đề bài ta có \(\dfrac{{n\left( {n - 1} \right)}}{2} = 28\) nên \(n\left( {n - 1} \right) = 56\) mà \(56 = 8.7\), lại có $(n-1)$ và $n$ là hai số tự nhiên liên tiếp nên \(n = 8.\)
Vậy \(n = 8.\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Đáp án : C
Ta sử dụng công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Tính số góc ban đầu
+ Tính số góc sau khi thêm
+ Tính số góc tăng thêm
Số góc tạo thành khi có \(4\) tia chung gốc là \(\dfrac{{4.\left( {4 - 1} \right)}}{2} = 6\) góc
Số góc tạo thành khi có thêm ba tia chung gốc \(O\) nữa là \(\dfrac{{7.\left( {7 - 1} \right)}}{2} = 21\) góc
Số góc tăng thêm là \(21 - 6 = 15\) góc
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Đáp án : D
+ Xác định số lượng các tia phân biệt chung gốc \(O.\)
+ Tính góc theo công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Vì có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) nên số các tia chung gốc tạo thành là \(2n\) tia.
Số góc tạo thành là \(\dfrac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right)\) góc.
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Đáp án : C
Sử dụng: Khi hai tia \(Ox;Oy\) không đối nhau, điểm \(M\) là điểm nằm bên trong góc \(xOy\) nếu tia \(OM\) nằm giữa hai tia \(Ox;Oy\).
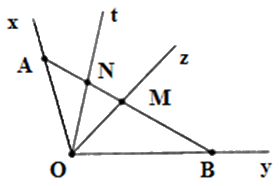
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) mà điểm \(N\) thuộc tia \(Ot\) nên điểm \(N\) nằm trong góc \(xOz\). Do đó A đúng.
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(N\) và điểm \(A\) nằm cùng phía đối với điểm \(M.\)
Tia \(Oz\) nằm giữa hai tia \(Ox;Oy\) nên điểm \(A;B\) nằm khác phía đối với điểm \(M.\) Suy ra điểm \(N\) và điểm \(B\) nằm khác phía đối với điểm \(M\), do đó điểm \(M\) nằm trong góc \(yOt.\) Do đó B đúng, D đúng.
Vì \(A \in Ox\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(A\) không nằm trong góc \(tOz.\) Do đó C sai.
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Chọn câu sai.
Góc vuông là góc có số đo bằng \(90^\circ \)
Góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) là góc nhọn
Góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \)
Góc có số đo nhỏ hơn \(180^\circ \) là góc tù
Chọn phát biểu đúng.
Góc có số đo \(120^\circ \) là góc vuông
Góc có số đo \(80^\circ \) là góc tù
Góc có số đo \(100^\circ \) là góc nhọn
Góc có số đo \(150^\circ \) là góc tù
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Góc trên hình có số đo bao nhiêu độ

\(50^\circ \)
\(40^\circ \)
\(60^\circ \)
\(130^\circ \)
Cho hình vẽ sau

Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ

\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau

\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Cho \(\widehat {xOm} = 45^\circ \) và góc \(xOm\) bằng góc \(yAn\). Khi đó số đo góc \(yAn\) bằng
\(50^\circ \)
\(40^\circ \)
\(45^\circ \)
\(30^\circ \)
Cho các góc sau \(\widehat A = 30^\circ ;\,\widehat B = 60^\circ ;\,\widehat C = 110^\circ ;\widehat D = 90^\circ \). Chọn câu sai.
\(\widehat B < \widehat D\)
\(\widehat C < \widehat D\)
\(\widehat A < \widehat B\)
\(\widehat B < \widehat C\)
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Đáp án : B
Sử dụng kiến thức về góc và so sánh hai góc
Để so sánh hai góc ta so sánh số đo của chúng
Ta có:
+ Góc là hình gồm hai tia chung gốc nên A đúng
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau
+ Hai góc bằng nhau có số đo bằng nhau nên C đúng
+ Hai góc có số đo bằng nhau thì bằng nhau nên D đúng
Chọn câu sai.
Góc vuông là góc có số đo bằng \(90^\circ \)
Góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) là góc nhọn
Góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \)
Góc có số đo nhỏ hơn \(180^\circ \) là góc tù
Đáp án : D
Ta có góc vuông là góc có số đo bằng \(90^\circ \); Góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) là góc nhọn
và góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \) nên A, B, C đều đúng.
Góc có số đo nhỏ hơn \(180^\circ \) là góc tù là sai vì góc nhọn, góc vuông đều có số đo nhỏ hơn \(180^\circ .\)
Chọn phát biểu đúng.
Góc có số đo \(120^\circ \) là góc vuông
Góc có số đo \(80^\circ \) là góc tù
Góc có số đo \(100^\circ \) là góc nhọn
Góc có số đo \(150^\circ \) là góc tù
Đáp án : D
Ta sử dụng các kiến thức:
Góc vuông là góc có số đo bằng \(90^\circ \);
Góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) là góc nhọn
Góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \)
+ Vì \(90^\circ < 120^\circ < 180^\circ \) nên góc có số đo \(120^\circ \) là góc tù, do đó A sai
+ Vì \(0^\circ < 80^\circ < 90^\circ \) nên góc có số đo \(80^\circ \) là góc nhọn, do đó B sai
+ Vì \(90^\circ < 100^\circ < 180^\circ \) nên góc có số đo \(100^\circ \) là góc tù, do đó C sai
+ Vì \(90^\circ < 150^\circ < 180^\circ \) nên góc có số đo \(150^\circ \) là góc tù, do đó D đúng
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Đáp án : C
Ta sử dụng kiến thức:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Số góc tạo thành là \(\dfrac{{9.\left( {9 - 1} \right)}}{2} = 36\) góc.
Góc trên hình có số đo bao nhiêu độ

\(50^\circ \)
\(40^\circ \)
\(60^\circ \)
\(130^\circ \)
Đáp án : A
Quan sát số chỉ giá trị ở vòng trong thước đo độ
Góc trên hình có số đo \(50^\circ .\)
Cho hình vẽ sau

Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Đáp án : A
Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc.
Góc trên hình là góc \(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ

\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Đáp án : B
Quan sát hình vẽ, xác định các tia phân biệt chung gốc \(O\) từ đó tìm các góc tạo thành.
Các góc tạo thành là: \(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau

\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Đáp án : D
Xác định các tia chung gốc \(O\) từ đó xác định các góc có một cạnh là \(Om.\)
Các góc cần tìm là \(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\) .
Cho \(\widehat {xOm} = 45^\circ \) và góc \(xOm\) bằng góc \(yAn\). Khi đó số đo góc \(yAn\) bằng
\(50^\circ \)
\(40^\circ \)
\(45^\circ \)
\(30^\circ \)
Đáp án : C
Sử dụng: Hai góc bằng nhau có số đo bằng nhau
Vì \(\widehat {xOm} = \widehat {yAn}\) mà \(\widehat {xOm} = 45^\circ \) nên \(\widehat {yAn} = 45^\circ .\)
Cho các góc sau \(\widehat A = 30^\circ ;\,\widehat B = 60^\circ ;\,\widehat C = 110^\circ ;\widehat D = 90^\circ \). Chọn câu sai.
\(\widehat B < \widehat D\)
\(\widehat C < \widehat D\)
\(\widehat A < \widehat B\)
\(\widehat B < \widehat C\)
Đáp án : B
Trong hai góc: Góc nào có số đo lớn hơn thì góc đó lớn hơn.
Ta có
+) \(60^\circ < 90^\circ \) nên \(\widehat B < \widehat D\) suy ra A đúng.
+) \(110^\circ > 90^\circ \) nên \(\widehat C > \widehat D\) suy ra B sai
+) \(30^\circ < 60^\circ \) nên \(\widehat A < \widehat B\) suy ra C đúng.
+) \(60^\circ < 110^\circ \) nên \(\widehat B < \widehat C\) suy ra D đúng.
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Đáp án : B
Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt.

Các tia \(Ox\) và \(Oy;\) \(Oz\) và \(Ot;Ou\) và \(Ov\) là hai tia đối nhau nên các góc bẹt có đỉnh \(O\) tạo thành là
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\) .
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Đáp án : A
Sử dụng:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Từ đó tìm ra \(n.\)
Từ đề bài ta có \(\dfrac{{n\left( {n - 1} \right)}}{2} = 28\) nên \(n\left( {n - 1} \right) = 56\) mà \(56 = 8.7\), lại có $(n-1)$ và $n$ là hai số tự nhiên liên tiếp nên \(n = 8.\)
Vậy \(n = 8.\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Đáp án : C
Ta sử dụng công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Tính số góc ban đầu
+ Tính số góc sau khi thêm
+ Tính số góc tăng thêm
Số góc tạo thành khi có \(4\) tia chung gốc là \(\dfrac{{4.\left( {4 - 1} \right)}}{2} = 6\) góc
Số góc tạo thành khi có thêm ba tia chung gốc \(O\) nữa là \(\dfrac{{7.\left( {7 - 1} \right)}}{2} = 21\) góc
Số góc tăng thêm là \(21 - 6 = 15\) góc
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Đáp án : D
+ Xác định số lượng các tia phân biệt chung gốc \(O.\)
+ Tính góc theo công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Vì có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) nên số các tia chung gốc tạo thành là \(2n\) tia.
Số góc tạo thành là \(\dfrac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right)\) góc.
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Đáp án : C
Sử dụng: Khi hai tia \(Ox;Oy\) không đối nhau, điểm \(M\) là điểm nằm bên trong góc \(xOy\) nếu tia \(OM\) nằm giữa hai tia \(Ox;Oy\).

Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) mà điểm \(N\) thuộc tia \(Ot\) nên điểm \(N\) nằm trong góc \(xOz\). Do đó A đúng.
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(N\) và điểm \(A\) nằm cùng phía đối với điểm \(M.\)
Tia \(Oz\) nằm giữa hai tia \(Ox;Oy\) nên điểm \(A;B\) nằm khác phía đối với điểm \(M.\) Suy ra điểm \(N\) và điểm \(B\) nằm khác phía đối với điểm \(M\), do đó điểm \(M\) nằm trong góc \(yOt.\) Do đó B đúng, D đúng.
Vì \(A \in Ox\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(A\) không nằm trong góc \(tOz.\) Do đó C sai.
Bài 5 trong chương trình Toán 6 Cánh diều tập trung vào khái niệm góc, các loại góc và cách đo góc. Đây là một trong những kiến thức nền tảng quan trọng trong hình học, giúp học sinh làm quen với các khái niệm cơ bản và phát triển tư duy không gian.
Dưới đây là một số ví dụ về các dạng bài tập trắc nghiệm thường gặp trong Bài 5: Góc Toán 6 Cánh diều:
Đáp án: C
Đáp án: C
Đáp án: C
Kiến thức về góc có ứng dụng rất lớn trong thực tế và trong các môn học khác. Ví dụ:
Giaitoan.edu.vn cam kết cung cấp cho học sinh những tài liệu học tập chất lượng, đầy đủ và cập nhật nhất. Chúng tôi luôn nỗ lực để tạo ra một môi trường học tập trực tuyến hiệu quả, giúp học sinh tự tin chinh phục môn Toán.
| Loại góc | Số đo |
|---|---|
| Góc nhọn | < 90° |
| Góc vuông | = 90° |
| Góc tù | > 90° và < 180° |
| Góc bẹt | = 180° |
Hy vọng với những kiến thức và bài tập trắc nghiệm trên, các em học sinh sẽ nắm vững kiến thức về góc và đạt kết quả tốt trong các bài kiểm tra Toán 6 Cánh diều.