Chào mừng các em học sinh lớp 6 đến với chuyên mục trắc nghiệm Toán 6 của giaitoan.edu.vn. Bài tập này tập trung vào các dạng toán về phép nhân và phép chia phân số, bám sát chương trình học Toán 6 Cánh diều.
Mục tiêu của chúng tôi là giúp các em ôn luyện và củng cố kiến thức một cách hiệu quả, chuẩn bị tốt nhất cho các bài kiểm tra và thi học kỳ.
Tính: \(\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}}\)
\(\dfrac{{ - 2}}{{27}}\)
\(\dfrac{{ - 4}}{9}\)
\(\dfrac{{ - 1}}{{18}}\)
\(\dfrac{{ - 3}}{2}\)
Chọn câu đúng.
\({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{ - 49}}{{36}}\)
\({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{8}{9}\)
\({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{8}{{ - 27}}\)
\({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{ - 16}}{{81}}\)
Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn \({\left( {\dfrac{{ - 5}}{3}} \right)^3} < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\) ?
$1$
\(0\)
\(2\)
\(3\)
Giá trị nào dưới đây của \(x\) thỏa mãn $x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}$
$\dfrac{5}{{56}}$
\(\dfrac{{ - 5}}{{56}}\)
\(\dfrac{5}{{28}}\)
\(\dfrac{{ - 5}}{{28}}\)
Có bao nhiêu giá trị của \(x\) thỏa mãn $\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}?$
$\dfrac{{17}}{{30}}$
\(\dfrac{{ - 11}}{{30}}\)
\(\dfrac{{ - 59}}{{30}}\)
\(\dfrac{{59}}{{30}}\)
Cho \(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\) và \(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\). Khi đó tổng \(M + N\) bằng
$\dfrac{{ - 62}}{{125}}$
\(\dfrac{{31}}{{1000}}\)
\(\dfrac{{ - 31}}{{100}}\)
\(\dfrac{{31}}{{100}}\)
Tính: \(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\) ta được
$\dfrac{9}{5}$
\(\dfrac{3}{5}\)
\(3\)
\(\dfrac{6}{5}\)
Tìm số tự nhiên \(x\) biết \(\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\)
\(\dfrac{{2019}}{{2021}}\)
\(2021\)
\(2020\)
\(2019\)
Tính \(M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{2}{{{2^{100}}}}\)
\(\dfrac{1}{{{2^{99}}}}\)
\(\dfrac{{{2^{101}} - 2}}{{{2^{100}}}}\)
\(\dfrac{{{2^{101}} + 1}}{{{2^{100}}}}\)
\(\dfrac{{{2^{101}} - 1}}{{{2^{100}}}}\)
Để làm bánh caramen, Linh cần \(\dfrac{4}{5}\) cốc đường để làm được \(10\) cái bánh. Vậy muốn làm \(15\) cái bánh thì Linh cần bao nhiêu cốc đường?
\(\dfrac{4}{5}\) cốc đường
\(1\) cốc đường
\(\dfrac{7}{5}\) cốc đường
\(\dfrac{6}{5}\) cốc đường
Tính giá trị biểu thức sau theo cách hợp lí
\(\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\)
\(\dfrac{4}{7}\)
\(\dfrac{{ - 4}}{7}\)
\( - 4\)
\(\dfrac{{11}}{7}\)
Một hình chữ nhật có diện tích \(\dfrac{{48}}{{35}}\) \(m^2\) và có chiều dài là \(\dfrac{6}{5}\) m. Tính chiều rộng của hình chữ nhật đó.
\(\dfrac{8}{7}\,\left( m \right)\)
\(\dfrac{7}{8}\,\left( m \right)\)
\(\dfrac{{36}}{7}\,\left( m \right)\)
\(\dfrac{{18}}{7}\,\left( m \right)\)
Tính: \(\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\)
\(\dfrac{1}{3}\)
\(\dfrac{{20}}{{13}}\)
\(3\)
\(\dfrac{{13}}{{20}}\)
Phân số nghịch đảo của số \( - 3\) là
$1$
\(3\)
\(\dfrac{1}{{ - 3}}\)
\(\dfrac{1}{3}\)
Kết quả của phép tính \(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right)\) là phân số có tử số là
$\dfrac{1}{4}$
\(\dfrac{1}{2}\)
\( - \dfrac{1}{2}\)
\(1\)
Giá trị nào dưới đây của \(x\) thỏa mãn \(\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\)?
$ - \dfrac{1}{{10}}$
\( - \dfrac{4}{9}\)
\( - \dfrac{4}{3}\)
\( - 4\)
Tính \(\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\)
$\dfrac{7}{{18}}$
\(\dfrac{9}{{14}}\)
\(\dfrac{{36}}{7}\)
\(\dfrac{{18}}{7}\)
Giá trị biểu thức \(M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\) là phân số tối giản có dạng \(\dfrac{a}{b}\) với \(a > 0.\) Tính \(b + a.\)
$8$
\(\dfrac{9}{5}\)
\(\dfrac{3}{5}\)
\(2\)
Rút gọn \(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\) ta được
$\dfrac{4}{3}$
\(1\)
\(0\)
\( - \dfrac{4}{3}\)
Cho \(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\) và \(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\) . Chọn kết luận đúng:
$P > Q$
\(P < Q\)
\(P < - Q\)
\(P = Q\)
Tìm \(x\) biết \(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
$\dfrac{9}{{64}}$
\(\dfrac{9}{{16}}\)
\(\dfrac{5}{{24}}\)
\(\dfrac{3}{8}\)
Giá trị của \(x\) thỏa mãn \(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}?\)
$ - \dfrac{1}{3}$
\(\dfrac{6}{5}\)
\( - \dfrac{3}{7}\)
\(\dfrac{3}{7}\)
Một hình chữ nhật có diện tích là \(\dfrac{8}{{15}}\,\left( {c{m^2}} \right)\), chiều dài là \(\dfrac{4}{3}\,\left( {cm} \right)\). Tính chu vi hình chữ nhật đó.
\(\dfrac{{52}}{5}\left( {cm} \right)\)
\(\dfrac{{26}}{{15}}\left( {cm} \right)\)
\(\dfrac{{52}}{{15}}\left( {cm} \right)\)
\(\dfrac{{52}}{{15}}\left( {c{m^2}} \right)\)
Số các số nguyên \(x\) để \(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) có giá trị là số nguyên là:
$1$
\(4\)
\(2\)
\(3\)
Một người đi xe máy, đi đoạn đường AB với vận tốc \(40km/h\) hết \(\dfrac{5}{4}\) giờ. Lúc về, người đó đi với vận tốc \(45km/h\). Tính thời gian người đó đi từ B về A?
\(\dfrac{{10}}{9}\)
\(\dfrac{{9}}{10}\)
\(\dfrac{{11}}{9}\)
\(2\)
Phân số \(\dfrac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\dfrac{{12}}{{35}};\) \(\dfrac{{18}}{{49}}\) cho \(\dfrac{a}{b}\) ta được kết quả là một số nguyên. Tính \(a + b.\)
\(245\)
\(251\)
\(158\)
\(496\)
Lời giải và đáp án
Tính: \(\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}}\)
\(\dfrac{{ - 2}}{{27}}\)
\(\dfrac{{ - 4}}{9}\)
\(\dfrac{{ - 1}}{{18}}\)
\(\dfrac{{ - 3}}{2}\)
Đáp án : A
Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Khi nhân ta chú ý rút gọn phân số.
$\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}} = \dfrac{{1.8}}{{12.\left( { - 9} \right)}}$$ = \dfrac{{1.2.4}}{{4.3.\left( { - 9} \right)}} = \dfrac{2}{{ - 27}} = \dfrac{{ - 2}}{{27}}$
Chọn câu đúng.
\({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{ - 49}}{{36}}\)
\({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{8}{9}\)
\({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{8}{{ - 27}}\)
\({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{ - 16}}{{81}}\)
Đáp án : C
Thực hiện các phép tính ở mỗi đáp án rồi kết luận đáp án đúng.
Sử dụng nhận xét lũy thừa của một phân số:
Với \(n \in N\) thì \({\left( {\dfrac{a}{b}} \right)^n} = \underbrace {\dfrac{a}{b}.\dfrac{a}{b}...\dfrac{a}{b}}_{n\,\,{\rm{thừa}}\,{\rm{số}}} = \dfrac{{{a^n}}}{{{b^n}}}\)
Đáp án A: \({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{{{\left( { - 7} \right)}^2}}}{{{6^2}}} = \dfrac{{49}}{{36}} \ne \dfrac{{ - 49}}{{36}}\) nên A sai.
Đáp án B: \({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{{{2^3}}}{{{3^3}}} = \dfrac{8}{{27}} \ne \dfrac{8}{9}\) nên B sai.
Đáp án C: \({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{{{2^3}}}{{{{\left( { - 3} \right)}^3}}} = \dfrac{8}{{ - 27}}\) nên C đúng.
Đáp án D: \({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{{{\left( { - 2} \right)}^4}}}{{{3^4}}} = \dfrac{{16}}{{81}} \ne \dfrac{{ - 16}}{{81}}\) nên D sai.
Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn \({\left( {\dfrac{{ - 5}}{3}} \right)^3} < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\) ?
$1$
\(0\)
\(2\)
\(3\)
Đáp án : B
Thực hiện các phép tính rồi tìm \(x\)
Chú ý \(x\) nguyên dương nên \(x > 0\)
Vì \(x\) nguyên dương nên \(x > 0\)
mà \({\left( {\dfrac{{ - 5}}{3}} \right)^3} = \dfrac{{ - 125}}{{27}} < 0\) nên
\({\left( {\dfrac{{ - 5}}{3}} \right)^3} < 0 < x <\dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6} \)
Khi đó:
\(0 < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\)
\(0 < x < \dfrac{4}{7}\)
Vì \(\dfrac{4}{7} < 1\) nên \(0 < x < 1\) nên không có số nguyên dương nào thỏa mãn.
Giá trị nào dưới đây của \(x\) thỏa mãn $x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}$
$\dfrac{5}{{56}}$
\(\dfrac{{ - 5}}{{56}}\)
\(\dfrac{5}{{28}}\)
\(\dfrac{{ - 5}}{{28}}\)
Đáp án : A
+ Tính vế phải theo qui tắc nhân phân số
+ Xác định rằng \(x\) là số bị chia bằng thương nhân với số chia
$\begin{array}{l}x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}\\x:\dfrac{5}{8} = \dfrac{{ - 2}}{5}.\dfrac{5}{{ - 14}}\\x:\dfrac{5}{8} = \dfrac{1}{7}\\x = \dfrac{1}{7}.\dfrac{5}{8}\\x = \dfrac{5}{{56}}\end{array}$
Có bao nhiêu giá trị của \(x\) thỏa mãn $\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}?$
$\dfrac{{17}}{{30}}$
\(\dfrac{{ - 11}}{{30}}\)
\(\dfrac{{ - 59}}{{30}}\)
\(\dfrac{{59}}{{30}}\)
Đáp án : C
- Tìm \(\dfrac{7}{6} + x\) dựa vào quy tắc muốn tìm số bị chia, ta lấy thương nhân số chia.
- Chuyển vế, đổi dấu và tìm \(x\)
$\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}$
\(\dfrac{7}{6} + x = \dfrac{{ - 5}}{4}.\dfrac{{16}}{{25}}\)
\(\dfrac{7}{6} + x = \dfrac{{ - 1}}{1}.\dfrac{4}{5}\)
\(\dfrac{7}{6} + x = \dfrac{{ - 4}}{5}\)
\(x = \dfrac{{ - 4}}{5} - \dfrac{7}{6}\)
\(x = \dfrac{{ - 59}}{{30}}\)
Cho \(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\) và \(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\). Khi đó tổng \(M + N\) bằng
$\dfrac{{ - 62}}{{125}}$
\(\dfrac{{31}}{{1000}}\)
\(\dfrac{{ - 31}}{{100}}\)
\(\dfrac{{31}}{{100}}\)
Đáp án : B
Thực hiện tính giá trị của hai biểu thức \(M,N\) rồi tính tổng \(M + N\)
\(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\)
\(M = \dfrac{{17.\left( { - 31} \right).1.10.{{\left( { - 1} \right)}^3}}}{{{{5.125.2.17.2}^3}}}\)
\(M = \dfrac{{ - 31.\left( { - 1} \right)}}{{{{125.2}^3}}}\)
\(M = \dfrac{{31}}{{1000}}\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{3}{{12}} + \dfrac{2}{{12}}} \right)\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).0\)
\(N = 0\)
Vậy \(M + N = \dfrac{{31}}{{1000}} + 0 = \dfrac{{31}}{{1000}}\)
Tính: \(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\) ta được
$\dfrac{9}{5}$
\(\dfrac{3}{5}\)
\(3\)
\(\dfrac{6}{5}\)
Đáp án : A
Để nhân nhiều phân số, ta nhân các tử số lại với nhau, các mẫu số nhân lại với nhau, sau đó rút gọn phân số.
\(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\)
\( = \dfrac{{2.2}}{{1.3}} \cdot \dfrac{{3.3}}{{2.4}} \cdot \dfrac{{4.4}}{{3.5}} \cdot \dfrac{{5.5}}{{4.6}} \cdot \dfrac{{6.6}}{{5.7}} \cdot \dfrac{{7.7}}{{6.8}} \cdot \dfrac{{8.8}}{{7.9}} \cdot \dfrac{{9.9}}{{8.10}}\)
\( = \dfrac{{2.3.4.5.6.7.8.9}}{{1.2.3.4.5.6.7.8}} \cdot \dfrac{{2.3.4.5.6.7.8.9}}{{3.4.5.6.7.8.9.10}}\)
\( = \dfrac{9}{1} \cdot \dfrac{2}{{10}} = \dfrac{{9.2}}{{1.10}} = \dfrac{9}{5}\)
Tìm số tự nhiên \(x\) biết \(\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\)
\(\dfrac{{2019}}{{2021}}\)
\(2021\)
\(2020\)
\(2019\)
Đáp án : C
Đặt 2 làm nhân tử chung, rút gọn và tìm x
\(\begin{array}{l}\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\\2.\left[ {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{x(x + 1)}}} \right] = \dfrac{{2019}}{{2021}}\\2.\left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right) = \dfrac{{2019}}{{2021}}\\2.\left( {\dfrac{1}{2} - \dfrac{1}{{x + 1}}} \right) = \dfrac{{2019}}{{2021}}\\1 - \dfrac{2}{{x + 1}} = \dfrac{{2019}}{{2021}}\\\dfrac{2}{{x + 1}} = 1 - \dfrac{{2019}}{{2021}}\\\dfrac{2}{{x + 1}} = \dfrac{2}{{2021}}\\x + 1 = 2021\\x = 2020\end{array}\)
Tính \(M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{2}{{{2^{100}}}}\)
\(\dfrac{1}{{{2^{99}}}}\)
\(\dfrac{{{2^{101}} - 2}}{{{2^{100}}}}\)
\(\dfrac{{{2^{101}} + 1}}{{{2^{100}}}}\)
\(\dfrac{{{2^{101}} - 1}}{{{2^{100}}}}\)
Đáp án : D
Nhân hai vế của biểu thức cho 2
Khai triển biểu thức đưa về tính hợp lý
\(\begin{array}{l}M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}\\2M = 2.\left( {1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}} \right)\\ = 2 + 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}}\end{array}\)
Ta có:
\(\begin{array}{l}M = 2M - M\\ = \left( {2 + 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{98}}}} + \dfrac{1}{{{2^{99}}}}} \right)\\ - \left( {1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}} \right)\\ = 2-\dfrac{1}{{{2^{100}}}} \\ =\dfrac{{{2^{101}} - 1}}{{{2^{100}}}} \end{array}\)
Để làm bánh caramen, Linh cần \(\dfrac{4}{5}\) cốc đường để làm được \(10\) cái bánh. Vậy muốn làm \(15\) cái bánh thì Linh cần bao nhiêu cốc đường?
\(\dfrac{4}{5}\) cốc đường
\(1\) cốc đường
\(\dfrac{7}{5}\) cốc đường
\(\dfrac{6}{5}\) cốc đường
Đáp án : D
Xác định để làm một cái bánh cần bao nhiêu phần cốc đường
Suy ra muốn làm 15 cái bánh thì cần bao nhiêu cốc đường.
Để làm một cái bánh thì cần lượng đường là: \(\dfrac{4}{5}.\dfrac{1}{{10}} = \dfrac{4}{{50}}\) (cốc đường)
Để làm 15 cái bánh thì cần số cốc đường là: \(\dfrac{4}{{50}}.15 = \dfrac{{60}}{{50}} = \dfrac{6}{5}\) (cốc đường)
Tính giá trị biểu thức sau theo cách hợp lí
\(\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\)
\(\dfrac{4}{7}\)
\(\dfrac{{ - 4}}{7}\)
\( - 4\)
\(\dfrac{{11}}{7}\)
Đáp án : A
Áp dụng tính chất: \(a.b + a.c = a.(b + c)\)
\(\begin{array}{l}\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\left( {\dfrac{{ - 4}}{{ - 5}} + \dfrac{3}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\left( {\dfrac{{ - 1}}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\dfrac{1}{5}\\ = \dfrac{{20}}{{35}} = \dfrac{4}{7}\end{array}\)
Một hình chữ nhật có diện tích \(\dfrac{{48}}{{35}}\) \(m^2\) và có chiều dài là \(\dfrac{6}{5}\) m. Tính chiều rộng của hình chữ nhật đó.
\(\dfrac{8}{7}\,\left( m \right)\)
\(\dfrac{7}{8}\,\left( m \right)\)
\(\dfrac{{36}}{7}\,\left( m \right)\)
\(\dfrac{{18}}{7}\,\left( m \right)\)
Đáp án : A
Diện tích hình chữ nhật = Chiều dài . chiều rộng
=> Chiều rộng = Diện tích : Chiều dài
Chiều rộng của hình chữ nhật là:
\(\dfrac{{48}}{{35}}:\dfrac{6}{5} = \dfrac{{48}}{{35}}.\dfrac{5}{6} = \dfrac{{6.8}}{{7.5}}.\dfrac{5}{6} = \dfrac{8}{7}\) (m)
Tính: \(\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\)
\(\dfrac{1}{3}\)
\(\dfrac{{20}}{{13}}\)
\(3\)
\(\dfrac{{13}}{{20}}\)
Đáp án : D
Thực hiện phép tính theo thứ tự: Lũy thừa => Phép tính trong ngoặc => Nhân, chia => Cộng, trừ.
\(\begin{array}{l}\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\\ = \dfrac{{28.1.3}}{{{{15.4}^2}}} + \left( {\dfrac{8}{{15}} - \dfrac{{23.3}}{{4.3.5}}.\dfrac{5}{{23}}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{{7.4.1.3}}{{3.5.4.4}} + \left( {\dfrac{8}{{15}} - \dfrac{1}{4}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \left( {\dfrac{{32}}{{60}} - \dfrac{{15}}{{60}}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \dfrac{{17}}{{60}}.\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \dfrac{{17}}{{6.10}}.\dfrac{{6.3.3}}{{17.3}}\\ = \dfrac{7}{{20}} + \dfrac{3}{{10}}\\ = \dfrac{7}{{20}} + \dfrac{6}{{20}}\\ = \dfrac{{13}}{{20}}\end{array}\)
Phân số nghịch đảo của số \( - 3\) là
$1$
\(3\)
\(\dfrac{1}{{ - 3}}\)
\(\dfrac{1}{3}\)
Đáp án : C
+ Phân số nghịch đảo của số nguyên \(a\,\left( {a \ne 0} \right)\) là \(\dfrac{1}{a}.\)
Phân số nghịch đảo của số \( - 3\) là \(\dfrac{1}{{ - 3}}\)
Kết quả của phép tính \(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right)\) là phân số có tử số là
$\dfrac{1}{4}$
\(\dfrac{1}{2}\)
\( - \dfrac{1}{2}\)
\(1\)
Đáp án : D
Muốn chia hai phân số, ta lấy phân số thứ nhất nhân với nghịch đảo của phân số thứ hai.
\(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right) = \dfrac{{ - 7}}{6}.\dfrac{{ - 3}}{{14}} = \dfrac{{1.1}}{{2.2}} = \dfrac{1}{4}\)
Phân số này có tử số là 1.
Giá trị nào dưới đây của \(x\) thỏa mãn \(\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\)?
$ - \dfrac{1}{{10}}$
\( - \dfrac{4}{9}\)
\( - \dfrac{4}{3}\)
\( - 4\)
Đáp án : B
Muốn tìm thừa số chưa biết trong phép nhân, ta lấy tích chia cho thừa số đã biết.
\(\begin{array}{l}\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\\x = \dfrac{4}{{15}}:\left( {\dfrac{{ - 3}}{5}} \right)\\x = \dfrac{4}{{15}}.\dfrac{5}{{ - 3}}\\x = - \dfrac{4}{9}\end{array}\)
Tính \(\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\)
$\dfrac{7}{{18}}$
\(\dfrac{9}{{14}}\)
\(\dfrac{{36}}{7}\)
\(\dfrac{{18}}{7}\)
Đáp án : C
Trong biểu thức chỉ chứa nhân, chia, ta thực hiện từ trái qua phải.
Chú ý: Muốn chia hai phân số, ta thực hiện nhân phân số thứ nhất với nghịch đảo của phân số thứ hai.
\(\begin{array}{l}\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\\ = \left( {\dfrac{2}{3}:\dfrac{7}{{12}}} \right):\dfrac{4}{{18}}\\ = \left( {\dfrac{2}{3}.\dfrac{{12}}{7}} \right):\dfrac{4}{{18}}\\ = \dfrac{8}{7}:\dfrac{4}{{18}}\\ = \dfrac{8}{7}.\dfrac{{18}}{4}\\ = \dfrac{{36}}{7}\end{array}\)
Giá trị biểu thức \(M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\) là phân số tối giản có dạng \(\dfrac{a}{b}\) với \(a > 0.\) Tính \(b + a.\)
$8$
\(\dfrac{9}{5}\)
\(\dfrac{3}{5}\)
\(2\)
Đáp án : A
Trong biểu thức chỉ chứa các toán cộng trừ nhân chia, ta thực hiện nhân chia trước, cộng trừ sau.
\(\begin{array}{l}M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\\M = \dfrac{5}{6}:\dfrac{{25}}{4} + \dfrac{7}{{15}}\\M = \dfrac{5}{6}.\dfrac{4}{{25}} + \dfrac{7}{{15}}\\M = \dfrac{{1.2}}{{3.5}} + \dfrac{7}{{15}}\\M = \dfrac{2}{{15}} + \dfrac{7}{{15}}\\M = \dfrac{9}{{15}} = \dfrac{3}{5}\end{array}\)
Khi đó \(a = 3,b = 5\) nên \(a + b = 8\)
Rút gọn \(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\) ta được
$\dfrac{4}{3}$
\(1\)
\(0\)
\( - \dfrac{4}{3}\)
Đáp án : A
Biến đổi tử và mẫu của \(N\) về dạng tích, rút gọn các thừa số chung của cả tử và mẫu rồi kết luận.
\(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\)\( = \dfrac{{4.\dfrac{1}{{17}} - 4.\dfrac{1}{{49}} - 4.\dfrac{1}{{131}}}}{{3.\dfrac{1}{{17}} - 3.\dfrac{1}{{49}} - 3.\dfrac{1}{{131}}}}\) \( = \dfrac{{4.\left( {\dfrac{1}{{17}} - \dfrac{1}{{49}} - \dfrac{1}{{131}}} \right)}}{{3.\left( {\dfrac{1}{{17}} - \dfrac{1}{{49}} - \dfrac{1}{{131}}} \right)}} = \dfrac{4}{3}\)
Cho \(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\) và \(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\) . Chọn kết luận đúng:
$P > Q$
\(P < Q\)
\(P < - Q\)
\(P = Q\)
Đáp án : A
Thực hiện tính giá trị các biểu thức \(P\) và \(Q\) rồi so sánh.
Chú ý: Trong biểu thức có chứa dấu ngoặc, ta ưu tiên thực hiện phép tính trong ngoặc trước, ngoài ngặc sau.
Biểu thức phức tạp nếu rút gọn được thì ta rút gọn nó trước rồi thực hiện tính toán.
\(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\)
\(P = \left( {\dfrac{{21}}{{60}} + \dfrac{{44}}{{60}} - \dfrac{{75}}{{60}}} \right):\left( {\dfrac{{99}}{{180}} - \dfrac{{104}}{{180}}} \right)\)
\(P = \dfrac{{ - 10}}{{60}}:\dfrac{{ - 5}}{{180}} = \dfrac{{ - 10}}{{60}}.\dfrac{{180}}{{ - 5}} = 6\)
\(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\)
\(Q = \dfrac{{5\left( {1 - \dfrac{1}{3} + \dfrac{1}{9} - \dfrac{1}{{27}}} \right)}}{{8\left( {1 - \dfrac{1}{3} + \dfrac{1}{9} - \dfrac{1}{{27}}} \right)}}:\dfrac{{15\left( {1 - \dfrac{1}{{11}} + \dfrac{1}{{121}}} \right)}}{{16\left( {1 - \dfrac{1}{{11}} + \dfrac{1}{{121}}} \right)}}\)
\(Q = \dfrac{5}{8}:\dfrac{{15}}{{16}} = \dfrac{5}{8}.\dfrac{{16}}{{15}} = \dfrac{2}{3}\)
Vì \(6 > \dfrac{2}{3}\) nên \(P > Q\)
Tìm \(x\) biết \(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
$\dfrac{9}{{64}}$
\(\dfrac{9}{{16}}\)
\(\dfrac{5}{{24}}\)
\(\dfrac{3}{8}\)
Đáp án : D
Thực hiện tính giá trị biểu thức trong ngoặc rồi sử dụng quy tắc tìm số bị chia trong phép chia, ta lấy thương nhân với số chia và quy tắc chuyển vế đổi dấu để tìm \(x\)
\(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
\(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\dfrac{{23}}{{12}} = \dfrac{7}{{46}}\)
\(x + \dfrac{1}{4} - \dfrac{1}{3} = \dfrac{7}{{46}}.\dfrac{{23}}{{12}}\)
\(x + \dfrac{1}{4} - \dfrac{1}{3} = \dfrac{7}{{24}}\)
\(x = \dfrac{7}{{24}} - \dfrac{1}{4} + \dfrac{1}{3}\)
\(x = \dfrac{3}{8}\)
Giá trị của \(x\) thỏa mãn \(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}?\)
$ - \dfrac{1}{3}$
\(\dfrac{6}{5}\)
\( - \dfrac{3}{7}\)
\(\dfrac{3}{7}\)
Đáp án : A
Áp dụng các kiến thức tìm số trừ trong phép trừ, tìm thừa số trong một tích và quy tắc chuyển vế đổi dấu để tìm \(x\)
\(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}\)
\(\left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{{13}}{{15}} - \dfrac{7}{{10}}\)
\(\left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{1}{6}\)
\(\dfrac{{13}}{{21}} + x = \dfrac{1}{6}:\dfrac{7}{{12}}\)
\(\dfrac{{13}}{{21}} + x = \dfrac{2}{7}\)
\(x = \dfrac{2}{7} - \dfrac{{13}}{{21}}\)
\(x = - \dfrac{1}{3}\)
Một hình chữ nhật có diện tích là \(\dfrac{8}{{15}}\,\left( {c{m^2}} \right)\), chiều dài là \(\dfrac{4}{3}\,\left( {cm} \right)\). Tính chu vi hình chữ nhật đó.
\(\dfrac{{52}}{5}\left( {cm} \right)\)
\(\dfrac{{26}}{{15}}\left( {cm} \right)\)
\(\dfrac{{52}}{{15}}\left( {cm} \right)\)
\(\dfrac{{52}}{{15}}\left( {c{m^2}} \right)\)
Đáp án : C
+ Tính chiều rộng hình chữ nhật bằng cách lấy diện tích chia cho chiều dài
+ Tính chu vi hình chữ nhật bằng cách lấy tổng chiều dài và chiều rộng tất cả nhân hai.
Chiều rộng hình chữ nhật là: \(\dfrac{8}{{15}}:\dfrac{4}{3} = \dfrac{2}{5}\left( {cm} \right)\)
Cho vi hình chữ nhật là: \(\left( {\dfrac{4}{3} + \dfrac{2}{5}} \right).2 = \dfrac{{52}}{{15}}\left( {cm} \right)\)
Số các số nguyên \(x\) để \(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) có giá trị là số nguyên là:
$1$
\(4\)
\(2\)
\(3\)
Đáp án : B
- Rút gọn biểu thức đã cho.
- Biểu thức \(\dfrac{a}{{mx + n}}\) với \(a,m,n \in Z\) có giá trị là số nguyên nếu \(mx + n \in Ư\left( a \right)\)
\(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) \( = \dfrac{{5x}}{3}.\dfrac{{21}}{{10{x^2} + 5x}}\) \( = \dfrac{{5x.21}}{{3.5x.\left( {2x + 1} \right)}}\) \( = \dfrac{7}{{2x + 1}}\)
Để biểu thức đã cho có giá trị là số nguyên thì \(\dfrac{7}{{2x + 1}}\) nguyên
Do đó \(2x + 1 \in Ư\left( 7 \right) = \left\{ { \pm 1; \pm 7} \right\}\)
Ta có bảng:
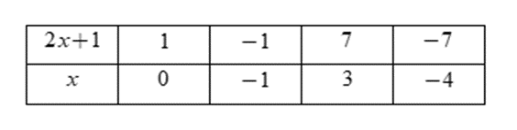
Vậy \(x \in \left\{ {0; - 1;3; - 4} \right\}\) suy ra có \(4\) giá trị thỏa mãn.
Một người đi xe máy, đi đoạn đường AB với vận tốc \(40km/h\) hết \(\dfrac{5}{4}\) giờ. Lúc về, người đó đi với vận tốc \(45km/h\). Tính thời gian người đó đi từ B về A?
\(\dfrac{{10}}{9}\)
\(\dfrac{{9}}{10}\)
\(\dfrac{{11}}{9}\)
\(2\)
Đáp án : A
Tìm quãng đường AB
Tính thời gian đi từ A đến B: thời gian = quãng đường chia cho vận tốc
Quãng đường AB là: \(40.\dfrac{5}{4} = 50\) (km)
Thời gian người đó đi từ B về A là: \(\dfrac{{50}}{{45}} = \dfrac{{10}}{9}\) (giờ)
Phân số \(\dfrac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\dfrac{{12}}{{35}};\) \(\dfrac{{18}}{{49}}\) cho \(\dfrac{a}{b}\) ta được kết quả là một số nguyên. Tính \(a + b.\)
\(245\)
\(251\)
\(158\)
\(496\)
Đáp án : B
Lập luận để đưa về tính chia hết của tử và mẫu của phân số cần tìm.
Từ đó tìm được phân số và tính tổng của tử và mẫu.
Gọi phân số lớn nhất cần tìm là: \(\dfrac{a}{b}\) (\(a;b\) là nguyên tố cùng nhau)
Ta có: \(\dfrac{{12}}{{35}}:\dfrac{a}{b} = \dfrac{{12b}}{{35{\rm{a}}}}\) là số nguyên, mà \(12;35\) là nguyên tố cùng nhau
Nên \(12 \vdots a;b \vdots 35\)
Ta lại có: \(\dfrac{{18}}{{49}}:\dfrac{a}{b} = \dfrac{{18b}}{{49{\rm{a}}}}\) là số nguyên, mà \(18\) và \(49\) nguyên tố cùng nhau
Nên \(18 \vdots a;b \vdots 49\)
Để \(\dfrac{a}{b}\) lớn nhất ta có \(a = UCLN(12;18) = 6\) và \(b = BCNN(35;49) = 245\)
Vậy tổng \(a + b = 6 + 245 = 251\)
Tính: \(\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}}\)
\(\dfrac{{ - 2}}{{27}}\)
\(\dfrac{{ - 4}}{9}\)
\(\dfrac{{ - 1}}{{18}}\)
\(\dfrac{{ - 3}}{2}\)
Chọn câu đúng.
\({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{ - 49}}{{36}}\)
\({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{8}{9}\)
\({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{8}{{ - 27}}\)
\({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{ - 16}}{{81}}\)
Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn \({\left( {\dfrac{{ - 5}}{3}} \right)^3} < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\) ?
$1$
\(0\)
\(2\)
\(3\)
Giá trị nào dưới đây của \(x\) thỏa mãn $x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}$
$\dfrac{5}{{56}}$
\(\dfrac{{ - 5}}{{56}}\)
\(\dfrac{5}{{28}}\)
\(\dfrac{{ - 5}}{{28}}\)
Có bao nhiêu giá trị của \(x\) thỏa mãn $\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}?$
$\dfrac{{17}}{{30}}$
\(\dfrac{{ - 11}}{{30}}\)
\(\dfrac{{ - 59}}{{30}}\)
\(\dfrac{{59}}{{30}}\)
Cho \(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\) và \(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\). Khi đó tổng \(M + N\) bằng
$\dfrac{{ - 62}}{{125}}$
\(\dfrac{{31}}{{1000}}\)
\(\dfrac{{ - 31}}{{100}}\)
\(\dfrac{{31}}{{100}}\)
Tính: \(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\) ta được
$\dfrac{9}{5}$
\(\dfrac{3}{5}\)
\(3\)
\(\dfrac{6}{5}\)
Tìm số tự nhiên \(x\) biết \(\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\)
\(\dfrac{{2019}}{{2021}}\)
\(2021\)
\(2020\)
\(2019\)
Tính \(M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{2}{{{2^{100}}}}\)
\(\dfrac{1}{{{2^{99}}}}\)
\(\dfrac{{{2^{101}} - 2}}{{{2^{100}}}}\)
\(\dfrac{{{2^{101}} + 1}}{{{2^{100}}}}\)
\(\dfrac{{{2^{101}} - 1}}{{{2^{100}}}}\)
Để làm bánh caramen, Linh cần \(\dfrac{4}{5}\) cốc đường để làm được \(10\) cái bánh. Vậy muốn làm \(15\) cái bánh thì Linh cần bao nhiêu cốc đường?
\(\dfrac{4}{5}\) cốc đường
\(1\) cốc đường
\(\dfrac{7}{5}\) cốc đường
\(\dfrac{6}{5}\) cốc đường
Tính giá trị biểu thức sau theo cách hợp lí
\(\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\)
\(\dfrac{4}{7}\)
\(\dfrac{{ - 4}}{7}\)
\( - 4\)
\(\dfrac{{11}}{7}\)
Một hình chữ nhật có diện tích \(\dfrac{{48}}{{35}}\) \(m^2\) và có chiều dài là \(\dfrac{6}{5}\) m. Tính chiều rộng của hình chữ nhật đó.
\(\dfrac{8}{7}\,\left( m \right)\)
\(\dfrac{7}{8}\,\left( m \right)\)
\(\dfrac{{36}}{7}\,\left( m \right)\)
\(\dfrac{{18}}{7}\,\left( m \right)\)
Tính: \(\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\)
\(\dfrac{1}{3}\)
\(\dfrac{{20}}{{13}}\)
\(3\)
\(\dfrac{{13}}{{20}}\)
Phân số nghịch đảo của số \( - 3\) là
$1$
\(3\)
\(\dfrac{1}{{ - 3}}\)
\(\dfrac{1}{3}\)
Kết quả của phép tính \(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right)\) là phân số có tử số là
$\dfrac{1}{4}$
\(\dfrac{1}{2}\)
\( - \dfrac{1}{2}\)
\(1\)
Giá trị nào dưới đây của \(x\) thỏa mãn \(\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\)?
$ - \dfrac{1}{{10}}$
\( - \dfrac{4}{9}\)
\( - \dfrac{4}{3}\)
\( - 4\)
Tính \(\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\)
$\dfrac{7}{{18}}$
\(\dfrac{9}{{14}}\)
\(\dfrac{{36}}{7}\)
\(\dfrac{{18}}{7}\)
Giá trị biểu thức \(M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\) là phân số tối giản có dạng \(\dfrac{a}{b}\) với \(a > 0.\) Tính \(b + a.\)
$8$
\(\dfrac{9}{5}\)
\(\dfrac{3}{5}\)
\(2\)
Rút gọn \(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\) ta được
$\dfrac{4}{3}$
\(1\)
\(0\)
\( - \dfrac{4}{3}\)
Cho \(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\) và \(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\) . Chọn kết luận đúng:
$P > Q$
\(P < Q\)
\(P < - Q\)
\(P = Q\)
Tìm \(x\) biết \(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
$\dfrac{9}{{64}}$
\(\dfrac{9}{{16}}\)
\(\dfrac{5}{{24}}\)
\(\dfrac{3}{8}\)
Giá trị của \(x\) thỏa mãn \(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}?\)
$ - \dfrac{1}{3}$
\(\dfrac{6}{5}\)
\( - \dfrac{3}{7}\)
\(\dfrac{3}{7}\)
Một hình chữ nhật có diện tích là \(\dfrac{8}{{15}}\,\left( {c{m^2}} \right)\), chiều dài là \(\dfrac{4}{3}\,\left( {cm} \right)\). Tính chu vi hình chữ nhật đó.
\(\dfrac{{52}}{5}\left( {cm} \right)\)
\(\dfrac{{26}}{{15}}\left( {cm} \right)\)
\(\dfrac{{52}}{{15}}\left( {cm} \right)\)
\(\dfrac{{52}}{{15}}\left( {c{m^2}} \right)\)
Số các số nguyên \(x\) để \(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) có giá trị là số nguyên là:
$1$
\(4\)
\(2\)
\(3\)
Một người đi xe máy, đi đoạn đường AB với vận tốc \(40km/h\) hết \(\dfrac{5}{4}\) giờ. Lúc về, người đó đi với vận tốc \(45km/h\). Tính thời gian người đó đi từ B về A?
\(\dfrac{{10}}{9}\)
\(\dfrac{{9}}{10}\)
\(\dfrac{{11}}{9}\)
\(2\)
Phân số \(\dfrac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\dfrac{{12}}{{35}};\) \(\dfrac{{18}}{{49}}\) cho \(\dfrac{a}{b}\) ta được kết quả là một số nguyên. Tính \(a + b.\)
\(245\)
\(251\)
\(158\)
\(496\)
Tính: \(\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}}\)
\(\dfrac{{ - 2}}{{27}}\)
\(\dfrac{{ - 4}}{9}\)
\(\dfrac{{ - 1}}{{18}}\)
\(\dfrac{{ - 3}}{2}\)
Đáp án : A
Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Khi nhân ta chú ý rút gọn phân số.
$\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}} = \dfrac{{1.8}}{{12.\left( { - 9} \right)}}$$ = \dfrac{{1.2.4}}{{4.3.\left( { - 9} \right)}} = \dfrac{2}{{ - 27}} = \dfrac{{ - 2}}{{27}}$
Chọn câu đúng.
\({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{ - 49}}{{36}}\)
\({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{8}{9}\)
\({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{8}{{ - 27}}\)
\({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{ - 16}}{{81}}\)
Đáp án : C
Thực hiện các phép tính ở mỗi đáp án rồi kết luận đáp án đúng.
Sử dụng nhận xét lũy thừa của một phân số:
Với \(n \in N\) thì \({\left( {\dfrac{a}{b}} \right)^n} = \underbrace {\dfrac{a}{b}.\dfrac{a}{b}...\dfrac{a}{b}}_{n\,\,{\rm{thừa}}\,{\rm{số}}} = \dfrac{{{a^n}}}{{{b^n}}}\)
Đáp án A: \({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{{{\left( { - 7} \right)}^2}}}{{{6^2}}} = \dfrac{{49}}{{36}} \ne \dfrac{{ - 49}}{{36}}\) nên A sai.
Đáp án B: \({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{{{2^3}}}{{{3^3}}} = \dfrac{8}{{27}} \ne \dfrac{8}{9}\) nên B sai.
Đáp án C: \({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{{{2^3}}}{{{{\left( { - 3} \right)}^3}}} = \dfrac{8}{{ - 27}}\) nên C đúng.
Đáp án D: \({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{{{\left( { - 2} \right)}^4}}}{{{3^4}}} = \dfrac{{16}}{{81}} \ne \dfrac{{ - 16}}{{81}}\) nên D sai.
Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn \({\left( {\dfrac{{ - 5}}{3}} \right)^3} < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\) ?
$1$
\(0\)
\(2\)
\(3\)
Đáp án : B
Thực hiện các phép tính rồi tìm \(x\)
Chú ý \(x\) nguyên dương nên \(x > 0\)
Vì \(x\) nguyên dương nên \(x > 0\)
mà \({\left( {\dfrac{{ - 5}}{3}} \right)^3} = \dfrac{{ - 125}}{{27}} < 0\) nên
\({\left( {\dfrac{{ - 5}}{3}} \right)^3} < 0 < x <\dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6} \)
Khi đó:
\(0 < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\)
\(0 < x < \dfrac{4}{7}\)
Vì \(\dfrac{4}{7} < 1\) nên \(0 < x < 1\) nên không có số nguyên dương nào thỏa mãn.
Giá trị nào dưới đây của \(x\) thỏa mãn $x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}$
$\dfrac{5}{{56}}$
\(\dfrac{{ - 5}}{{56}}\)
\(\dfrac{5}{{28}}\)
\(\dfrac{{ - 5}}{{28}}\)
Đáp án : A
+ Tính vế phải theo qui tắc nhân phân số
+ Xác định rằng \(x\) là số bị chia bằng thương nhân với số chia
$\begin{array}{l}x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}\\x:\dfrac{5}{8} = \dfrac{{ - 2}}{5}.\dfrac{5}{{ - 14}}\\x:\dfrac{5}{8} = \dfrac{1}{7}\\x = \dfrac{1}{7}.\dfrac{5}{8}\\x = \dfrac{5}{{56}}\end{array}$
Có bao nhiêu giá trị của \(x\) thỏa mãn $\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}?$
$\dfrac{{17}}{{30}}$
\(\dfrac{{ - 11}}{{30}}\)
\(\dfrac{{ - 59}}{{30}}\)
\(\dfrac{{59}}{{30}}\)
Đáp án : C
- Tìm \(\dfrac{7}{6} + x\) dựa vào quy tắc muốn tìm số bị chia, ta lấy thương nhân số chia.
- Chuyển vế, đổi dấu và tìm \(x\)
$\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}$
\(\dfrac{7}{6} + x = \dfrac{{ - 5}}{4}.\dfrac{{16}}{{25}}\)
\(\dfrac{7}{6} + x = \dfrac{{ - 1}}{1}.\dfrac{4}{5}\)
\(\dfrac{7}{6} + x = \dfrac{{ - 4}}{5}\)
\(x = \dfrac{{ - 4}}{5} - \dfrac{7}{6}\)
\(x = \dfrac{{ - 59}}{{30}}\)
Cho \(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\) và \(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\). Khi đó tổng \(M + N\) bằng
$\dfrac{{ - 62}}{{125}}$
\(\dfrac{{31}}{{1000}}\)
\(\dfrac{{ - 31}}{{100}}\)
\(\dfrac{{31}}{{100}}\)
Đáp án : B
Thực hiện tính giá trị của hai biểu thức \(M,N\) rồi tính tổng \(M + N\)
\(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\)
\(M = \dfrac{{17.\left( { - 31} \right).1.10.{{\left( { - 1} \right)}^3}}}{{{{5.125.2.17.2}^3}}}\)
\(M = \dfrac{{ - 31.\left( { - 1} \right)}}{{{{125.2}^3}}}\)
\(M = \dfrac{{31}}{{1000}}\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{3}{{12}} + \dfrac{2}{{12}}} \right)\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).0\)
\(N = 0\)
Vậy \(M + N = \dfrac{{31}}{{1000}} + 0 = \dfrac{{31}}{{1000}}\)
Tính: \(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\) ta được
$\dfrac{9}{5}$
\(\dfrac{3}{5}\)
\(3\)
\(\dfrac{6}{5}\)
Đáp án : A
Để nhân nhiều phân số, ta nhân các tử số lại với nhau, các mẫu số nhân lại với nhau, sau đó rút gọn phân số.
\(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\)
\( = \dfrac{{2.2}}{{1.3}} \cdot \dfrac{{3.3}}{{2.4}} \cdot \dfrac{{4.4}}{{3.5}} \cdot \dfrac{{5.5}}{{4.6}} \cdot \dfrac{{6.6}}{{5.7}} \cdot \dfrac{{7.7}}{{6.8}} \cdot \dfrac{{8.8}}{{7.9}} \cdot \dfrac{{9.9}}{{8.10}}\)
\( = \dfrac{{2.3.4.5.6.7.8.9}}{{1.2.3.4.5.6.7.8}} \cdot \dfrac{{2.3.4.5.6.7.8.9}}{{3.4.5.6.7.8.9.10}}\)
\( = \dfrac{9}{1} \cdot \dfrac{2}{{10}} = \dfrac{{9.2}}{{1.10}} = \dfrac{9}{5}\)
Tìm số tự nhiên \(x\) biết \(\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\)
\(\dfrac{{2019}}{{2021}}\)
\(2021\)
\(2020\)
\(2019\)
Đáp án : C
Đặt 2 làm nhân tử chung, rút gọn và tìm x
\(\begin{array}{l}\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\\2.\left[ {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{x(x + 1)}}} \right] = \dfrac{{2019}}{{2021}}\\2.\left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right) = \dfrac{{2019}}{{2021}}\\2.\left( {\dfrac{1}{2} - \dfrac{1}{{x + 1}}} \right) = \dfrac{{2019}}{{2021}}\\1 - \dfrac{2}{{x + 1}} = \dfrac{{2019}}{{2021}}\\\dfrac{2}{{x + 1}} = 1 - \dfrac{{2019}}{{2021}}\\\dfrac{2}{{x + 1}} = \dfrac{2}{{2021}}\\x + 1 = 2021\\x = 2020\end{array}\)
Tính \(M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{2}{{{2^{100}}}}\)
\(\dfrac{1}{{{2^{99}}}}\)
\(\dfrac{{{2^{101}} - 2}}{{{2^{100}}}}\)
\(\dfrac{{{2^{101}} + 1}}{{{2^{100}}}}\)
\(\dfrac{{{2^{101}} - 1}}{{{2^{100}}}}\)
Đáp án : D
Nhân hai vế của biểu thức cho 2
Khai triển biểu thức đưa về tính hợp lý
\(\begin{array}{l}M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}\\2M = 2.\left( {1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}} \right)\\ = 2 + 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}}\end{array}\)
Ta có:
\(\begin{array}{l}M = 2M - M\\ = \left( {2 + 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{98}}}} + \dfrac{1}{{{2^{99}}}}} \right)\\ - \left( {1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}} \right)\\ = 2-\dfrac{1}{{{2^{100}}}} \\ =\dfrac{{{2^{101}} - 1}}{{{2^{100}}}} \end{array}\)
Để làm bánh caramen, Linh cần \(\dfrac{4}{5}\) cốc đường để làm được \(10\) cái bánh. Vậy muốn làm \(15\) cái bánh thì Linh cần bao nhiêu cốc đường?
\(\dfrac{4}{5}\) cốc đường
\(1\) cốc đường
\(\dfrac{7}{5}\) cốc đường
\(\dfrac{6}{5}\) cốc đường
Đáp án : D
Xác định để làm một cái bánh cần bao nhiêu phần cốc đường
Suy ra muốn làm 15 cái bánh thì cần bao nhiêu cốc đường.
Để làm một cái bánh thì cần lượng đường là: \(\dfrac{4}{5}.\dfrac{1}{{10}} = \dfrac{4}{{50}}\) (cốc đường)
Để làm 15 cái bánh thì cần số cốc đường là: \(\dfrac{4}{{50}}.15 = \dfrac{{60}}{{50}} = \dfrac{6}{5}\) (cốc đường)
Tính giá trị biểu thức sau theo cách hợp lí
\(\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\)
\(\dfrac{4}{7}\)
\(\dfrac{{ - 4}}{7}\)
\( - 4\)
\(\dfrac{{11}}{7}\)
Đáp án : A
Áp dụng tính chất: \(a.b + a.c = a.(b + c)\)
\(\begin{array}{l}\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\left( {\dfrac{{ - 4}}{{ - 5}} + \dfrac{3}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\left( {\dfrac{{ - 1}}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\dfrac{1}{5}\\ = \dfrac{{20}}{{35}} = \dfrac{4}{7}\end{array}\)
Một hình chữ nhật có diện tích \(\dfrac{{48}}{{35}}\) \(m^2\) và có chiều dài là \(\dfrac{6}{5}\) m. Tính chiều rộng của hình chữ nhật đó.
\(\dfrac{8}{7}\,\left( m \right)\)
\(\dfrac{7}{8}\,\left( m \right)\)
\(\dfrac{{36}}{7}\,\left( m \right)\)
\(\dfrac{{18}}{7}\,\left( m \right)\)
Đáp án : A
Diện tích hình chữ nhật = Chiều dài . chiều rộng
=> Chiều rộng = Diện tích : Chiều dài
Chiều rộng của hình chữ nhật là:
\(\dfrac{{48}}{{35}}:\dfrac{6}{5} = \dfrac{{48}}{{35}}.\dfrac{5}{6} = \dfrac{{6.8}}{{7.5}}.\dfrac{5}{6} = \dfrac{8}{7}\) (m)
Tính: \(\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\)
\(\dfrac{1}{3}\)
\(\dfrac{{20}}{{13}}\)
\(3\)
\(\dfrac{{13}}{{20}}\)
Đáp án : D
Thực hiện phép tính theo thứ tự: Lũy thừa => Phép tính trong ngoặc => Nhân, chia => Cộng, trừ.
\(\begin{array}{l}\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\\ = \dfrac{{28.1.3}}{{{{15.4}^2}}} + \left( {\dfrac{8}{{15}} - \dfrac{{23.3}}{{4.3.5}}.\dfrac{5}{{23}}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{{7.4.1.3}}{{3.5.4.4}} + \left( {\dfrac{8}{{15}} - \dfrac{1}{4}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \left( {\dfrac{{32}}{{60}} - \dfrac{{15}}{{60}}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \dfrac{{17}}{{60}}.\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \dfrac{{17}}{{6.10}}.\dfrac{{6.3.3}}{{17.3}}\\ = \dfrac{7}{{20}} + \dfrac{3}{{10}}\\ = \dfrac{7}{{20}} + \dfrac{6}{{20}}\\ = \dfrac{{13}}{{20}}\end{array}\)
Phân số nghịch đảo của số \( - 3\) là
$1$
\(3\)
\(\dfrac{1}{{ - 3}}\)
\(\dfrac{1}{3}\)
Đáp án : C
+ Phân số nghịch đảo của số nguyên \(a\,\left( {a \ne 0} \right)\) là \(\dfrac{1}{a}.\)
Phân số nghịch đảo của số \( - 3\) là \(\dfrac{1}{{ - 3}}\)
Kết quả của phép tính \(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right)\) là phân số có tử số là
$\dfrac{1}{4}$
\(\dfrac{1}{2}\)
\( - \dfrac{1}{2}\)
\(1\)
Đáp án : D
Muốn chia hai phân số, ta lấy phân số thứ nhất nhân với nghịch đảo của phân số thứ hai.
\(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right) = \dfrac{{ - 7}}{6}.\dfrac{{ - 3}}{{14}} = \dfrac{{1.1}}{{2.2}} = \dfrac{1}{4}\)
Phân số này có tử số là 1.
Giá trị nào dưới đây của \(x\) thỏa mãn \(\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\)?
$ - \dfrac{1}{{10}}$
\( - \dfrac{4}{9}\)
\( - \dfrac{4}{3}\)
\( - 4\)
Đáp án : B
Muốn tìm thừa số chưa biết trong phép nhân, ta lấy tích chia cho thừa số đã biết.
\(\begin{array}{l}\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\\x = \dfrac{4}{{15}}:\left( {\dfrac{{ - 3}}{5}} \right)\\x = \dfrac{4}{{15}}.\dfrac{5}{{ - 3}}\\x = - \dfrac{4}{9}\end{array}\)
Tính \(\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\)
$\dfrac{7}{{18}}$
\(\dfrac{9}{{14}}\)
\(\dfrac{{36}}{7}\)
\(\dfrac{{18}}{7}\)
Đáp án : C
Trong biểu thức chỉ chứa nhân, chia, ta thực hiện từ trái qua phải.
Chú ý: Muốn chia hai phân số, ta thực hiện nhân phân số thứ nhất với nghịch đảo của phân số thứ hai.
\(\begin{array}{l}\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\\ = \left( {\dfrac{2}{3}:\dfrac{7}{{12}}} \right):\dfrac{4}{{18}}\\ = \left( {\dfrac{2}{3}.\dfrac{{12}}{7}} \right):\dfrac{4}{{18}}\\ = \dfrac{8}{7}:\dfrac{4}{{18}}\\ = \dfrac{8}{7}.\dfrac{{18}}{4}\\ = \dfrac{{36}}{7}\end{array}\)
Giá trị biểu thức \(M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\) là phân số tối giản có dạng \(\dfrac{a}{b}\) với \(a > 0.\) Tính \(b + a.\)
$8$
\(\dfrac{9}{5}\)
\(\dfrac{3}{5}\)
\(2\)
Đáp án : A
Trong biểu thức chỉ chứa các toán cộng trừ nhân chia, ta thực hiện nhân chia trước, cộng trừ sau.
\(\begin{array}{l}M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\\M = \dfrac{5}{6}:\dfrac{{25}}{4} + \dfrac{7}{{15}}\\M = \dfrac{5}{6}.\dfrac{4}{{25}} + \dfrac{7}{{15}}\\M = \dfrac{{1.2}}{{3.5}} + \dfrac{7}{{15}}\\M = \dfrac{2}{{15}} + \dfrac{7}{{15}}\\M = \dfrac{9}{{15}} = \dfrac{3}{5}\end{array}\)
Khi đó \(a = 3,b = 5\) nên \(a + b = 8\)
Rút gọn \(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\) ta được
$\dfrac{4}{3}$
\(1\)
\(0\)
\( - \dfrac{4}{3}\)
Đáp án : A
Biến đổi tử và mẫu của \(N\) về dạng tích, rút gọn các thừa số chung của cả tử và mẫu rồi kết luận.
\(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\)\( = \dfrac{{4.\dfrac{1}{{17}} - 4.\dfrac{1}{{49}} - 4.\dfrac{1}{{131}}}}{{3.\dfrac{1}{{17}} - 3.\dfrac{1}{{49}} - 3.\dfrac{1}{{131}}}}\) \( = \dfrac{{4.\left( {\dfrac{1}{{17}} - \dfrac{1}{{49}} - \dfrac{1}{{131}}} \right)}}{{3.\left( {\dfrac{1}{{17}} - \dfrac{1}{{49}} - \dfrac{1}{{131}}} \right)}} = \dfrac{4}{3}\)
Cho \(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\) và \(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\) . Chọn kết luận đúng:
$P > Q$
\(P < Q\)
\(P < - Q\)
\(P = Q\)
Đáp án : A
Thực hiện tính giá trị các biểu thức \(P\) và \(Q\) rồi so sánh.
Chú ý: Trong biểu thức có chứa dấu ngoặc, ta ưu tiên thực hiện phép tính trong ngoặc trước, ngoài ngặc sau.
Biểu thức phức tạp nếu rút gọn được thì ta rút gọn nó trước rồi thực hiện tính toán.
\(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\)
\(P = \left( {\dfrac{{21}}{{60}} + \dfrac{{44}}{{60}} - \dfrac{{75}}{{60}}} \right):\left( {\dfrac{{99}}{{180}} - \dfrac{{104}}{{180}}} \right)\)
\(P = \dfrac{{ - 10}}{{60}}:\dfrac{{ - 5}}{{180}} = \dfrac{{ - 10}}{{60}}.\dfrac{{180}}{{ - 5}} = 6\)
\(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\)
\(Q = \dfrac{{5\left( {1 - \dfrac{1}{3} + \dfrac{1}{9} - \dfrac{1}{{27}}} \right)}}{{8\left( {1 - \dfrac{1}{3} + \dfrac{1}{9} - \dfrac{1}{{27}}} \right)}}:\dfrac{{15\left( {1 - \dfrac{1}{{11}} + \dfrac{1}{{121}}} \right)}}{{16\left( {1 - \dfrac{1}{{11}} + \dfrac{1}{{121}}} \right)}}\)
\(Q = \dfrac{5}{8}:\dfrac{{15}}{{16}} = \dfrac{5}{8}.\dfrac{{16}}{{15}} = \dfrac{2}{3}\)
Vì \(6 > \dfrac{2}{3}\) nên \(P > Q\)
Tìm \(x\) biết \(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
$\dfrac{9}{{64}}$
\(\dfrac{9}{{16}}\)
\(\dfrac{5}{{24}}\)
\(\dfrac{3}{8}\)
Đáp án : D
Thực hiện tính giá trị biểu thức trong ngoặc rồi sử dụng quy tắc tìm số bị chia trong phép chia, ta lấy thương nhân với số chia và quy tắc chuyển vế đổi dấu để tìm \(x\)
\(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
\(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\dfrac{{23}}{{12}} = \dfrac{7}{{46}}\)
\(x + \dfrac{1}{4} - \dfrac{1}{3} = \dfrac{7}{{46}}.\dfrac{{23}}{{12}}\)
\(x + \dfrac{1}{4} - \dfrac{1}{3} = \dfrac{7}{{24}}\)
\(x = \dfrac{7}{{24}} - \dfrac{1}{4} + \dfrac{1}{3}\)
\(x = \dfrac{3}{8}\)
Giá trị của \(x\) thỏa mãn \(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}?\)
$ - \dfrac{1}{3}$
\(\dfrac{6}{5}\)
\( - \dfrac{3}{7}\)
\(\dfrac{3}{7}\)
Đáp án : A
Áp dụng các kiến thức tìm số trừ trong phép trừ, tìm thừa số trong một tích và quy tắc chuyển vế đổi dấu để tìm \(x\)
\(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}\)
\(\left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{{13}}{{15}} - \dfrac{7}{{10}}\)
\(\left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{1}{6}\)
\(\dfrac{{13}}{{21}} + x = \dfrac{1}{6}:\dfrac{7}{{12}}\)
\(\dfrac{{13}}{{21}} + x = \dfrac{2}{7}\)
\(x = \dfrac{2}{7} - \dfrac{{13}}{{21}}\)
\(x = - \dfrac{1}{3}\)
Một hình chữ nhật có diện tích là \(\dfrac{8}{{15}}\,\left( {c{m^2}} \right)\), chiều dài là \(\dfrac{4}{3}\,\left( {cm} \right)\). Tính chu vi hình chữ nhật đó.
\(\dfrac{{52}}{5}\left( {cm} \right)\)
\(\dfrac{{26}}{{15}}\left( {cm} \right)\)
\(\dfrac{{52}}{{15}}\left( {cm} \right)\)
\(\dfrac{{52}}{{15}}\left( {c{m^2}} \right)\)
Đáp án : C
+ Tính chiều rộng hình chữ nhật bằng cách lấy diện tích chia cho chiều dài
+ Tính chu vi hình chữ nhật bằng cách lấy tổng chiều dài và chiều rộng tất cả nhân hai.
Chiều rộng hình chữ nhật là: \(\dfrac{8}{{15}}:\dfrac{4}{3} = \dfrac{2}{5}\left( {cm} \right)\)
Cho vi hình chữ nhật là: \(\left( {\dfrac{4}{3} + \dfrac{2}{5}} \right).2 = \dfrac{{52}}{{15}}\left( {cm} \right)\)
Số các số nguyên \(x\) để \(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) có giá trị là số nguyên là:
$1$
\(4\)
\(2\)
\(3\)
Đáp án : B
- Rút gọn biểu thức đã cho.
- Biểu thức \(\dfrac{a}{{mx + n}}\) với \(a,m,n \in Z\) có giá trị là số nguyên nếu \(mx + n \in Ư\left( a \right)\)
\(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) \( = \dfrac{{5x}}{3}.\dfrac{{21}}{{10{x^2} + 5x}}\) \( = \dfrac{{5x.21}}{{3.5x.\left( {2x + 1} \right)}}\) \( = \dfrac{7}{{2x + 1}}\)
Để biểu thức đã cho có giá trị là số nguyên thì \(\dfrac{7}{{2x + 1}}\) nguyên
Do đó \(2x + 1 \in Ư\left( 7 \right) = \left\{ { \pm 1; \pm 7} \right\}\)
Ta có bảng:

Vậy \(x \in \left\{ {0; - 1;3; - 4} \right\}\) suy ra có \(4\) giá trị thỏa mãn.
Một người đi xe máy, đi đoạn đường AB với vận tốc \(40km/h\) hết \(\dfrac{5}{4}\) giờ. Lúc về, người đó đi với vận tốc \(45km/h\). Tính thời gian người đó đi từ B về A?
\(\dfrac{{10}}{9}\)
\(\dfrac{{9}}{10}\)
\(\dfrac{{11}}{9}\)
\(2\)
Đáp án : A
Tìm quãng đường AB
Tính thời gian đi từ A đến B: thời gian = quãng đường chia cho vận tốc
Quãng đường AB là: \(40.\dfrac{5}{4} = 50\) (km)
Thời gian người đó đi từ B về A là: \(\dfrac{{50}}{{45}} = \dfrac{{10}}{9}\) (giờ)
Phân số \(\dfrac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\dfrac{{12}}{{35}};\) \(\dfrac{{18}}{{49}}\) cho \(\dfrac{a}{b}\) ta được kết quả là một số nguyên. Tính \(a + b.\)
\(245\)
\(251\)
\(158\)
\(496\)
Đáp án : B
Lập luận để đưa về tính chia hết của tử và mẫu của phân số cần tìm.
Từ đó tìm được phân số và tính tổng của tử và mẫu.
Gọi phân số lớn nhất cần tìm là: \(\dfrac{a}{b}\) (\(a;b\) là nguyên tố cùng nhau)
Ta có: \(\dfrac{{12}}{{35}}:\dfrac{a}{b} = \dfrac{{12b}}{{35{\rm{a}}}}\) là số nguyên, mà \(12;35\) là nguyên tố cùng nhau
Nên \(12 \vdots a;b \vdots 35\)
Ta lại có: \(\dfrac{{18}}{{49}}:\dfrac{a}{b} = \dfrac{{18b}}{{49{\rm{a}}}}\) là số nguyên, mà \(18\) và \(49\) nguyên tố cùng nhau
Nên \(18 \vdots a;b \vdots 49\)
Để \(\dfrac{a}{b}\) lớn nhất ta có \(a = UCLN(12;18) = 6\) và \(b = BCNN(35;49) = 245\)
Vậy tổng \(a + b = 6 + 245 = 251\)
Phép nhân và phép chia phân số là một trong những chủ đề quan trọng trong chương trình Toán 6 Cánh diều. Việc nắm vững các quy tắc và kỹ năng giải toán liên quan đến hai phép tính này là nền tảng để học tốt các kiến thức toán học nâng cao hơn. Bài viết này sẽ cung cấp một cái nhìn tổng quan về các dạng toán thường gặp trong phép nhân và phép chia phân số, cùng với các ví dụ minh họa và hướng dẫn giải chi tiết.
1. Quy tắc nhân hai phân số:
Để nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu số với nhau. Tức là:
a/b * c/d = (a * c) / (b * d)
2. Các tính chất của phép nhân phân số:
3. Dạng toán thường gặp:
1. Quy tắc chia hai phân số:
Để chia hai phân số, ta thực hiện phép nhân phân số thứ nhất với phân số nghịch đảo của phân số thứ hai. Tức là:
a/b : c/d = a/b * d/c = (a * d) / (b * c)
2. Phân số nghịch đảo:
Phân số nghịch đảo của phân số a/b là b/a (với a ≠ 0 và b ≠ 0).
3. Dạng toán thường gặp:
Trong nhiều bài toán, chúng ta cần kết hợp cả phép nhân và phép chia phân số để tìm ra kết quả. Khi đó, cần thực hiện các phép tính theo đúng thứ tự ưu tiên: nhân, chia trước, cộng, trừ sau.
Ví dụ: Tính giá trị của biểu thức:
(3/4 * 2/5) : 1/2
Giải:
Vậy, giá trị của biểu thức là 3/5.
Để nắm vững kiến thức và kỹ năng giải toán về phép nhân và phép chia phân số, các em hãy tham gia các bài trắc nghiệm tại giaitoan.edu.vn. Các bài trắc nghiệm được thiết kế đa dạng, bao gồm nhiều dạng toán khác nhau, giúp các em rèn luyện tư duy và kỹ năng giải quyết vấn đề.
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải các bài toán về phép nhân và phép chia phân số Toán 6 Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi!