Chào mừng bạn đến với chuyên mục Trắc nghiệm Bài tập cuối chương VI Toán 6 Cánh diều của giaitoan.edu.vn. Đây là công cụ hỗ trợ học tập tuyệt vời, giúp các em học sinh ôn luyện và củng cố kiến thức đã học trong chương.
Với hình thức trắc nghiệm đa dạng, bài tập được thiết kế bám sát chương trình học, cùng đáp án và lời giải chi tiết, các em sẽ dễ dàng tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
\(1\)
\(2\)
\(3\)
Vô số
Cho hình vẽ. Em hãy chọn đáp án đúng.

A nằm giữa hai điểm B và C
B nằm giữa hai điểm A và C
C nằm giữa hai điểm A và B
Không có điểm nào nằm giữa hai điểm còn lại
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Tia NM trùng với tia MP
Tia MP trùng với tia NP
Tia PM trùng với tia PN
Tia MN trùng với tia MP.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
$5$
$3$
$4$
$2$
Cho hình vẽ sau. Chọn câu đúng.
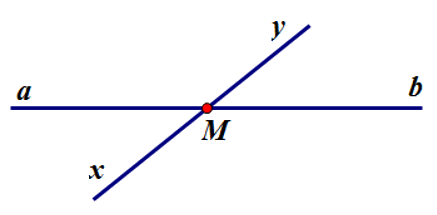
Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
Hai đường thẳng xy và ab không có điểm chung
Đường thẳng xy cắt đường thẳng ab tại M
Đường thẳng xy và ab có hai điểm chung
Cho hình vẽ sau. Chọn câu đúng.
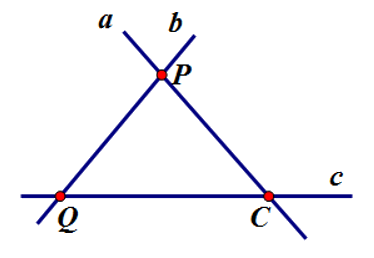
\(P \in a;P \in c\)
\(Q \in b;Q \in c\)
Đường thẳng a cắt đường thẳng c tại điểm P
Không có hai đường thẳng nào cắt nhau trên hình vẽ
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
$0$
$1$ hoặc $2$
$4$
$3$
Cho hình vẽ. Em hãy chọn khẳng định sai:

NM và NI là hai tia đối nhau
IN và IM là hai tia trùng nhau
MN và MI là hai tia trùng nhau
MN và NI là hai tia trùng nhau
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:
$3cm$
$2cm$
$5cm$
$7cm$
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là
$8cm$
$16cm$
$24cm$
$28cm$
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
\(4cm\)
\(5cm\)
\(2cm\)
\(3cm\)
Lấy năm điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
$3$
$10$
$12$
$4$
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
$15$
$16$
$14$
$13$
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
\(276\)
\(290\)
\(262\)
\(226\)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.
\(MO = 4cm\)
\(MO = 3cm\)
\(MO = 1cm\)
\(MO = 2cm\)
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
Điểm I là trung điểm của OM
Điểm O nằm giữa I và P
\(IP = 2cm\)
Cả A, B, C đều đúng.
Em hãy chọn phát biểu sai trong các phát biểu sau:
Góc bẹt là góc có hai cạnh là hai tia đối nhau
\(\widehat A\) được gọi là góc tù nếu \(\widehat A > {90^0}\)
Nếu tia Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Tam giác $MNP$ là hình gồm các đoạn thẳng $MN, MP$ và $NP$ khi ba điểm $M, N, P$ không thẳng hàng.
Cho ba điểm không thẳng hàng $O, A, B.$ Tia $Ox$ nằm giữa hai tia $OA, OB$ khi và chỉ khi tia $Ox$ cắt
Đoạn thẳng $AB$
Đường thẳng $AB$
Tia $AB$
Tia $BA$
Cho \(100\) tia gồm \(O{x_2},O{x_3},....,O{x_{99}}\) nằm giữa hai tia \(O{x_1}\) và \(O{x_{100}}\). Hỏi có bao nhiêu góc được tạo thành?
\(9702\) góc
\(4553\) góc
\(4950\) góc
\(4851\) góc
Lời giải và đáp án
Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
\(1\)
\(2\)
\(3\)
Vô số
Đáp án : A
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước.
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước. Vậy có duy nhất 1 đường thẳng đi qua hai điểm A và B.
Cho hình vẽ. Em hãy chọn đáp án đúng.

A nằm giữa hai điểm B và C
B nằm giữa hai điểm A và C
C nằm giữa hai điểm A và B
Không có điểm nào nằm giữa hai điểm còn lại
Đáp án : B
Quan sát hình vẽ và xác định điểm nằm giữa hai điểm còn lại
Quan sát hình vẽ ta thấy điểm B nằm giữa hai điểm A và C.
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Tia NM trùng với tia MP
Tia MP trùng với tia NP
Tia PM trùng với tia PN
Tia MN trùng với tia MP.
Đáp án : C
Hai tia trùng nhau là hai tia chung gốc và tạo thành nửa đường thẳng.
Nhận xét:
+ Đáp án A: Hai tia NM và MP là hai tia không chung gốc nên loại đáp án A.
+ Đáp án B: Hai tia MP và NP là hai tia không chung gốc nên loại đáp án B.
+ Đáp án C: thấy hai tia PN và PM là hai tia cùng chung gốc P và tạo thành nửa đường thẳng nên hai tia PN và PM là hai tia trùng nhau, do đó chọn đáp án C.
+ Đáp án D: Hai tia MN và MP là hai tia chung gốc nhưng tạo thành một đường thẳng nên hai tia MN và MP là hai tia đối nhau, do đó loại đáp án D.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
$5$
$3$
$4$
$2$
Đáp án : A
Ta liệt kê tất cả các tia chung gốc B, kể cả các tia trùng nhau.

Hình vẽ trên có các tia chung gốc B là: BA, Bx, By, BC và BD. Vậy có tất cả 5 tia chung gốc B.
Cho hình vẽ sau. Chọn câu đúng.
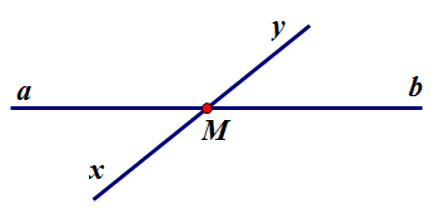
Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
Hai đường thẳng xy và ab không có điểm chung
Đường thẳng xy cắt đường thẳng ab tại M
Đường thẳng xy và ab có hai điểm chung
Đáp án : C
Quan sát hình vẽ và sử dụng kiến thức về điểm, đường thẳng
Ta thấy hai đường thẳng xy và ab cắt nhau tại M nên đáp án C đúng.
Cho hình vẽ sau. Chọn câu đúng.
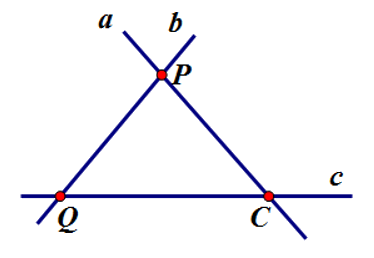
\(P \in a;P \in c\)
\(Q \in b;Q \in c\)
Đường thẳng a cắt đường thẳng c tại điểm P
Không có hai đường thẳng nào cắt nhau trên hình vẽ
Đáp án : B
Quan sát hình vẽ và sử dụng kiến thức về điểm và đường thẳng
Từ hình vẽ ta thấy \(P \in a;P \in c\) nên đáp án A sai; \(Q \in b;Q \in c\) nên đáp án B đúng.
Hai đường thẳng a và c cắt nhau tại điểm C nên đáp án C sai.
Đáp án D sai vì ta thấy có ba cặp đường thẳng cắt nhau trên hình vẽ là a và c, a và b, b và c.
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
$0$
$1$ hoặc $2$
$4$
$3$
Đáp án : C
Hai đường thẳng phân biệt bất kì có thể song song, cắt nhau, trùng nhau.
Với 3 đường thẳng phân biệt ta có các trường hợp sau:
+ Không có đường thẳng nào cắt nhau nên không có điểm chung.
+ Hai đường thẳng cắt nhau, đường thẳng còn lại không cắt hai đường thẳng đó, khi đó có 1 điểm chung.
+ Ba đường thẳng đó có đôi một cắt nhau thì có ba điểm chung.
Vậy không thể có trường hợp ba đường thẳng phân biệt bất kì mà có 4 điểm chung.
Cho hình vẽ. Em hãy chọn khẳng định sai:

NM và NI là hai tia đối nhau
IN và IM là hai tia trùng nhau
MN và MI là hai tia trùng nhau
MN và NI là hai tia trùng nhau
Đáp án : D
Dựa vào định nghĩa và tính chất các tia đối nhau và trùng nhau:
+ Hai tia đối nhau phải chung gốc, phải tạo thành 1 đường thẳng.
+ Hai tia trùng nhau là hai tia có chung gốc và có thêm ít nhất 1 điểm chung.
Từ hình vẽ ta thấy các điểm M, N, I cùng thuộc một đường thẳng.
+) Hai tia NM và NI đối nhau vì chúng chung gốc N và tạo thành một đường thẳng, từ đó loại đáp án A.
+) Hai tia IN và IM trùng nhau vì chúng chung gốc I và có thêm điểm chung là N, từ đó loại đáp án B.
+) Hai tia MN và MI trùng nhau vì chúng chung gốc M và có thêm điểm chung là N, từ đó loại đáp án C.
+) Hai tia MN và NI không trùng nhau vì chúng không chung gốc.
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:
$3cm$
$2cm$
$5cm$
$7cm$
Đáp án : D
Vì L nằm giữa I và K nên ta áp dụng công thức cộng đoạn thẳng.

Vì L nằm giữa I và K nên ta có:\(IL + LK = IK \Rightarrow IK = 2 + 5 = 7cm\)
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là
$8cm$
$16cm$
$24cm$
$28cm$
Đáp án : C
Dựa vào tính chất trung điểm của đoạn thẳng: Nếu M là trung điểm của đoạn thẳng AB thì
${\rm{MA = MB}} = \dfrac{1}{2}AB$.

Vì G là trung điểm của đoạn thẳng BC nên ${\rm{BG = }}\,GC = \dfrac{1}{2}BC = \dfrac{1}{2} \cdot 32 = 16\,cm$.
Vì H là trung điểm của đoạn thẳng GC nên ${\rm{GH }} = HC = {\rm{ }}\dfrac{1}{2}GC = \dfrac{1}{2} \cdot 16 = 8\,cm$.
Ta có G thuộc đoạn thẳng BC nên GB và GC là hai tia đối nhau. (1)
Vì H là trung điểm của GC nên H thuộc GC (2)
Từ (1) và (2) suy ra G là điểm nằm giữa hai điểm B và H.
\(\begin{array}{l} \Rightarrow BG + GH = BH\\ \Rightarrow 16 + 8 = BH\\ \Rightarrow BH = 24cm\end{array}\)
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Đáp án : A
Để điểm I nằm giữa hai điểm L và K là: $IL + IK = LK$
Điều kiện để điểm I nằm giữa hai điểm L và K là: \(IL + IK = LK\) nên \(4 + IK = 5 \Rightarrow IK = 5 - 4 = 1cm\)
Vậy điều kiện để điểm I nằm giữa hai điểm L và K là $IK = 1cm\;$
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
\(4cm\)
\(5cm\)
\(2cm\)
\(3cm\)
Đáp án : D
Bước 1: Chỉ ra điểm I nằm giữa hai điểm A và B Bước 2: Dựa vào tính chất cộng độ dài đoạn thẳng để tính IB
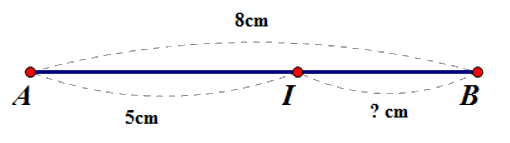
Vì điểm Ihuộc đoạn thẳng AB; $AI = 5cm,{\rm{ }}AB = 8cm$ mà $5cm < 8cm$ nên $AI < AB\;$
Suy ra điểm I nằm giữa hai điểm A và B $ \Rightarrow AI + IB = AB \Rightarrow 4cm + IB = 7cm \Rightarrow IB = 7cm - 4cm = 3cm$
Lấy năm điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
$3$
$10$
$12$
$4$
Đáp án : B
Áp dụng tính chất: Chỉ có duy nhất một đường thẳng đi qua hai điểm phân biệt.
Từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được các đường thẳng đi qua hai điểm bất kì như sau:
+ Với điểm M ta có thể nối với các điểm: N, P, Q, K để tạo thành 4 đường thẳng phân biệt.
+ Với điểm N ta có thể nối với các điểm: P, Q, K để tạo thành 3 đường thẳng phân biệt.
+ Với điểm P ta có thể nối với các điểm: Q, K để tạo thành 2 đường thẳng phân biệt.
+ Với điểm Q ta có thể nối với điểm K để tạo thành 1 đường thẳng .
Vậy từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được tất cả:
4 + 3 + 2 + 1 = 10 đường thẳng phân biệt.
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
$15$
$16$
$14$
$13$
Đáp án : A
Vì qua hai điểm phân biệt ta luôn vẽ được một đoạn thẳng nên ta tính số đoạn thẳng tạo thành từ n điểm phân biệt theo công thức: \(\dfrac{{n\left( {n - 1} \right)}}{2}\,\,\left( {n \ge 2} \right)\) đoạn thẳng
Vì qua 2 điểm luôn vẽ được một đoạn thẳng Nên qua 6 điểm vẽ được số đoạn thẳng là: \(\dfrac{{6\left( {6 - 1} \right)}}{2} = 15\) (đoạn thẳng)
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
\(276\)
\(290\)
\(262\)
\(226\)
Đáp án : C
Ta sử dụng công thức tính số đường thẳng tạo bởi n điểm phân biệt \(\left( {n \ge 2} \right)\) trong đó không có ba điểm nào thảng hàng: \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Giả sử 24 điểm không có 3 điểm nào thẳng hàng. Tính số đường thẳng vẽ được qua 24 điểm + Tính số đường thẳng vẽ được qua 6 điểm (giả sử 6 điểm không có 3 điểm nào thẳng hàng)
+ Số đường thẳng vẽ được qua 6 điểm thẳng hàng+ Tính số đường thẳng vẽ được qua 24 điểm trong đó có 6 điểm thẳng hàng
Giả sử trong 24 điểm không có 3 điểm nào thẳng hàng tất cả vẽ được: $\dfrac{{24.(24 - 1)}}{2} = 276$ (đường thẳng) Qua 6 điểm thẳng hàng vẽ được số đường thẳng là: $\dfrac{{6.(6 - 1)}}{2} = 15$ (đường thẳng) Nhưng qua 6 điểm thẳng hàng chỉ vẽ được một đường thẳng Nên qua 24 điểm trong đó có 6 điểm thẳng hàng vẽ được: $276 - 15 + 1 = 262$ (đường thẳng)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.
\(MO = 4cm\)
\(MO = 3cm\)
\(MO = 1cm\)
\(MO = 2cm\)
Đáp án: C
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.

+) Vì \(M \in AB\) nên M nằm giữa A và B
\( \Rightarrow AM + MB = AB \Rightarrow BM \)\(= AB - MB = 6 - 4 = 2cm.\)
+) Vì O là trung điểm của AB nên: \(AO = OB = \dfrac{{AB}}{2} \)\(= \dfrac{6}{2} = 3cm\)
Vì \(O \in AB\), \(M \in AB\) và \(AO < AM (3cm < 4cm)\) nên O nằm giữa A và M suy ra:
\(AO + OM = AM \Rightarrow OM\)\( = AM - AO = 4 - 3 = 1cm\)
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
Điểm I là trung điểm của OM
Điểm O nằm giữa I và P
\(IP = 2cm\)
Cả A, B, C đều đúng.
Đáp án: D
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.

+ ) Vì \(O \in AB\), \(I \in AB\) và AO < AI (3cm < 3,5cm) nên O nằm giữa A và I suy ra:
\(AO + OI = AI \)\(\Rightarrow OI = AI - AO = 3,5 - 3 = 0,5cm\) (1)
Vì \(I \in AB\), \(M \in AB\) và AI < AM (3,5cm < 4cm) nên I nằm giữa A và M suy ra:
\(AI + IM = AM \Rightarrow IM = AM - AI = 4 - 3,5 = 0,5cm\)(2)
Từ (1) và (2) suy ra $OI = IM$ . (3)
Vì O nằm giữa A và I nên A và O nằm cùng phía đối với I . Mà I nằm giữa A và M nên A và M nằm khác phía đối với I \( \Rightarrow \) O và M nằm khác phía đối với I suy ra I nằm giữa M và O (4)
Từ (3) và (4) suy ra I là trung điểm của OM.
+) Vì P là trung điểm của AO nên: \(OP = AP = \dfrac{{AO}}{2} = \dfrac{3}{2} = 1,5cm\)
Vì $\left\{ \begin{array}{l}O,M \in AB\\AO < AM\left( {3cm < 4cm} \right)\end{array} \right. \Rightarrow $ O nằm giữa A và M
Suy ra A và M nằm khác phía đối với O
Vì P là trung điểm của AO nên A, P cùng phía đối với O.
Vì I là trung điểm của OM nên I, M cùng phía đối với O.
Từ đó suy ra I nằm giữa O và P \( \Rightarrow OP + IO = IP \)\(\Rightarrow IP = 1,5 + 0,5 = 2cm\)
Em hãy chọn phát biểu sai trong các phát biểu sau:
Góc bẹt là góc có hai cạnh là hai tia đối nhau
\(\widehat A\) được gọi là góc tù nếu \(\widehat A > {90^0}\)
Nếu tia Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Tam giác $MNP$ là hình gồm các đoạn thẳng $MN, MP$ và $NP$ khi ba điểm $M, N, P$ không thẳng hàng.
Đáp án : B
Áp dụng các kiến thức về: số đo góc, tia phân giác, tam giác.
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau (đúng loại A)
+ \(\widehat A\) được gọi là góc tù nếu \(\widehat A > {90^0}\) (sai vì \(\widehat A\) được gọi là góc tù nếu \({90^0} < \widehat A < {180^0}\), chọn B)
+ Nếu tia Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)(đúng loại C)
+ Tam giác MNP là hình gồm các đoạn thẳng MN, MP và NP khi ba điểm M, N, P không thẳng hàng. (đúng loại D)
Cho ba điểm không thẳng hàng $O, A, B.$ Tia $Ox$ nằm giữa hai tia $OA, OB$ khi và chỉ khi tia $Ox$ cắt
Đoạn thẳng $AB$
Đường thẳng $AB$
Tia $AB$
Tia $BA$
Đáp án : A
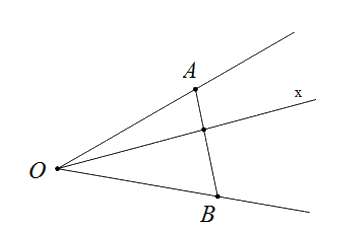
Tia $Ox$ nằm giữa hai tia $OA$ và $OB$ khi tia $Ox$ cắt đoạn thẳng $AB$
Cho \(100\) tia gồm \(O{x_2},O{x_3},....,O{x_{99}}\) nằm giữa hai tia \(O{x_1}\) và \(O{x_{100}}\). Hỏi có bao nhiêu góc được tạo thành?
\(9702\) góc
\(4553\) góc
\(4950\) góc
\(4851\) góc
Đáp án : C
Áp dụng định nghĩa góc, tính chất của dãy số cách đều.
- \(O{x_1}\) cùng với các tia \(O{x_2},O{x_3},....,O{x_{100}}\) tạo thành \(99\) góc.
- \(O{x_2}\) cùng với các tia \(O{x_3},....,O{x_{100}}\) tạo thành 98 góc.
- \(O{x_3}\) cùng với các tia \(O{x_4},O{x_5},....,O{x_{100}}\) tạo thành \(97\)góc.
…………
\(O{x_{99}}\) cùng tia \(O{x_{100}}\) tạo thành 1 góc.
Vậy ta có tất cả: \(1 + 2 + 3 + ... + 99 = \dfrac{{100.99}}{2} = 4950\) góc.
Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
\(1\)
\(2\)
\(3\)
Vô số
Cho hình vẽ. Em hãy chọn đáp án đúng.

A nằm giữa hai điểm B và C
B nằm giữa hai điểm A và C
C nằm giữa hai điểm A và B
Không có điểm nào nằm giữa hai điểm còn lại
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Tia NM trùng với tia MP
Tia MP trùng với tia NP
Tia PM trùng với tia PN
Tia MN trùng với tia MP.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
$5$
$3$
$4$
$2$
Cho hình vẽ sau. Chọn câu đúng.

Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
Hai đường thẳng xy và ab không có điểm chung
Đường thẳng xy cắt đường thẳng ab tại M
Đường thẳng xy và ab có hai điểm chung
Cho hình vẽ sau. Chọn câu đúng.

\(P \in a;P \in c\)
\(Q \in b;Q \in c\)
Đường thẳng a cắt đường thẳng c tại điểm P
Không có hai đường thẳng nào cắt nhau trên hình vẽ
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
$0$
$1$ hoặc $2$
$4$
$3$
Cho hình vẽ. Em hãy chọn khẳng định sai:

NM và NI là hai tia đối nhau
IN và IM là hai tia trùng nhau
MN và MI là hai tia trùng nhau
MN và NI là hai tia trùng nhau
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:
$3cm$
$2cm$
$5cm$
$7cm$
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là
$8cm$
$16cm$
$24cm$
$28cm$
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
\(4cm\)
\(5cm\)
\(2cm\)
\(3cm\)
Lấy năm điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
$3$
$10$
$12$
$4$
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
$15$
$16$
$14$
$13$
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
\(276\)
\(290\)
\(262\)
\(226\)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.
\(MO = 4cm\)
\(MO = 3cm\)
\(MO = 1cm\)
\(MO = 2cm\)
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
Điểm I là trung điểm của OM
Điểm O nằm giữa I và P
\(IP = 2cm\)
Cả A, B, C đều đúng.
Em hãy chọn phát biểu sai trong các phát biểu sau:
Góc bẹt là góc có hai cạnh là hai tia đối nhau
\(\widehat A\) được gọi là góc tù nếu \(\widehat A > {90^0}\)
Nếu tia Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Tam giác $MNP$ là hình gồm các đoạn thẳng $MN, MP$ và $NP$ khi ba điểm $M, N, P$ không thẳng hàng.
Cho ba điểm không thẳng hàng $O, A, B.$ Tia $Ox$ nằm giữa hai tia $OA, OB$ khi và chỉ khi tia $Ox$ cắt
Đoạn thẳng $AB$
Đường thẳng $AB$
Tia $AB$
Tia $BA$
Cho \(100\) tia gồm \(O{x_2},O{x_3},....,O{x_{99}}\) nằm giữa hai tia \(O{x_1}\) và \(O{x_{100}}\). Hỏi có bao nhiêu góc được tạo thành?
\(9702\) góc
\(4553\) góc
\(4950\) góc
\(4851\) góc
Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
\(1\)
\(2\)
\(3\)
Vô số
Đáp án : A
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước.
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước. Vậy có duy nhất 1 đường thẳng đi qua hai điểm A và B.
Cho hình vẽ. Em hãy chọn đáp án đúng.

A nằm giữa hai điểm B và C
B nằm giữa hai điểm A và C
C nằm giữa hai điểm A và B
Không có điểm nào nằm giữa hai điểm còn lại
Đáp án : B
Quan sát hình vẽ và xác định điểm nằm giữa hai điểm còn lại
Quan sát hình vẽ ta thấy điểm B nằm giữa hai điểm A và C.
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Tia NM trùng với tia MP
Tia MP trùng với tia NP
Tia PM trùng với tia PN
Tia MN trùng với tia MP.
Đáp án : C
Hai tia trùng nhau là hai tia chung gốc và tạo thành nửa đường thẳng.
Nhận xét:
+ Đáp án A: Hai tia NM và MP là hai tia không chung gốc nên loại đáp án A.
+ Đáp án B: Hai tia MP và NP là hai tia không chung gốc nên loại đáp án B.
+ Đáp án C: thấy hai tia PN và PM là hai tia cùng chung gốc P và tạo thành nửa đường thẳng nên hai tia PN và PM là hai tia trùng nhau, do đó chọn đáp án C.
+ Đáp án D: Hai tia MN và MP là hai tia chung gốc nhưng tạo thành một đường thẳng nên hai tia MN và MP là hai tia đối nhau, do đó loại đáp án D.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
$5$
$3$
$4$
$2$
Đáp án : A
Ta liệt kê tất cả các tia chung gốc B, kể cả các tia trùng nhau.

Hình vẽ trên có các tia chung gốc B là: BA, Bx, By, BC và BD. Vậy có tất cả 5 tia chung gốc B.
Cho hình vẽ sau. Chọn câu đúng.

Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
Hai đường thẳng xy và ab không có điểm chung
Đường thẳng xy cắt đường thẳng ab tại M
Đường thẳng xy và ab có hai điểm chung
Đáp án : C
Quan sát hình vẽ và sử dụng kiến thức về điểm, đường thẳng
Ta thấy hai đường thẳng xy và ab cắt nhau tại M nên đáp án C đúng.
Cho hình vẽ sau. Chọn câu đúng.

\(P \in a;P \in c\)
\(Q \in b;Q \in c\)
Đường thẳng a cắt đường thẳng c tại điểm P
Không có hai đường thẳng nào cắt nhau trên hình vẽ
Đáp án : B
Quan sát hình vẽ và sử dụng kiến thức về điểm và đường thẳng
Từ hình vẽ ta thấy \(P \in a;P \in c\) nên đáp án A sai; \(Q \in b;Q \in c\) nên đáp án B đúng.
Hai đường thẳng a và c cắt nhau tại điểm C nên đáp án C sai.
Đáp án D sai vì ta thấy có ba cặp đường thẳng cắt nhau trên hình vẽ là a và c, a và b, b và c.
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
$0$
$1$ hoặc $2$
$4$
$3$
Đáp án : C
Hai đường thẳng phân biệt bất kì có thể song song, cắt nhau, trùng nhau.
Với 3 đường thẳng phân biệt ta có các trường hợp sau:
+ Không có đường thẳng nào cắt nhau nên không có điểm chung.
+ Hai đường thẳng cắt nhau, đường thẳng còn lại không cắt hai đường thẳng đó, khi đó có 1 điểm chung.
+ Ba đường thẳng đó có đôi một cắt nhau thì có ba điểm chung.
Vậy không thể có trường hợp ba đường thẳng phân biệt bất kì mà có 4 điểm chung.
Cho hình vẽ. Em hãy chọn khẳng định sai:

NM và NI là hai tia đối nhau
IN và IM là hai tia trùng nhau
MN và MI là hai tia trùng nhau
MN và NI là hai tia trùng nhau
Đáp án : D
Dựa vào định nghĩa và tính chất các tia đối nhau và trùng nhau:
+ Hai tia đối nhau phải chung gốc, phải tạo thành 1 đường thẳng.
+ Hai tia trùng nhau là hai tia có chung gốc và có thêm ít nhất 1 điểm chung.
Từ hình vẽ ta thấy các điểm M, N, I cùng thuộc một đường thẳng.
+) Hai tia NM và NI đối nhau vì chúng chung gốc N và tạo thành một đường thẳng, từ đó loại đáp án A.
+) Hai tia IN và IM trùng nhau vì chúng chung gốc I và có thêm điểm chung là N, từ đó loại đáp án B.
+) Hai tia MN và MI trùng nhau vì chúng chung gốc M và có thêm điểm chung là N, từ đó loại đáp án C.
+) Hai tia MN và NI không trùng nhau vì chúng không chung gốc.
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:
$3cm$
$2cm$
$5cm$
$7cm$
Đáp án : D
Vì L nằm giữa I và K nên ta áp dụng công thức cộng đoạn thẳng.

Vì L nằm giữa I và K nên ta có:\(IL + LK = IK \Rightarrow IK = 2 + 5 = 7cm\)
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là
$8cm$
$16cm$
$24cm$
$28cm$
Đáp án : C
Dựa vào tính chất trung điểm của đoạn thẳng: Nếu M là trung điểm của đoạn thẳng AB thì
${\rm{MA = MB}} = \dfrac{1}{2}AB$.

Vì G là trung điểm của đoạn thẳng BC nên ${\rm{BG = }}\,GC = \dfrac{1}{2}BC = \dfrac{1}{2} \cdot 32 = 16\,cm$.
Vì H là trung điểm của đoạn thẳng GC nên ${\rm{GH }} = HC = {\rm{ }}\dfrac{1}{2}GC = \dfrac{1}{2} \cdot 16 = 8\,cm$.
Ta có G thuộc đoạn thẳng BC nên GB và GC là hai tia đối nhau. (1)
Vì H là trung điểm của GC nên H thuộc GC (2)
Từ (1) và (2) suy ra G là điểm nằm giữa hai điểm B và H.
\(\begin{array}{l} \Rightarrow BG + GH = BH\\ \Rightarrow 16 + 8 = BH\\ \Rightarrow BH = 24cm\end{array}\)
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Đáp án : A
Để điểm I nằm giữa hai điểm L và K là: $IL + IK = LK$
Điều kiện để điểm I nằm giữa hai điểm L và K là: \(IL + IK = LK\) nên \(4 + IK = 5 \Rightarrow IK = 5 - 4 = 1cm\)
Vậy điều kiện để điểm I nằm giữa hai điểm L và K là $IK = 1cm\;$
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
\(4cm\)
\(5cm\)
\(2cm\)
\(3cm\)
Đáp án : D
Bước 1: Chỉ ra điểm I nằm giữa hai điểm A và B Bước 2: Dựa vào tính chất cộng độ dài đoạn thẳng để tính IB

Vì điểm Ihuộc đoạn thẳng AB; $AI = 5cm,{\rm{ }}AB = 8cm$ mà $5cm < 8cm$ nên $AI < AB\;$
Suy ra điểm I nằm giữa hai điểm A và B $ \Rightarrow AI + IB = AB \Rightarrow 4cm + IB = 7cm \Rightarrow IB = 7cm - 4cm = 3cm$
Lấy năm điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
$3$
$10$
$12$
$4$
Đáp án : B
Áp dụng tính chất: Chỉ có duy nhất một đường thẳng đi qua hai điểm phân biệt.
Từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được các đường thẳng đi qua hai điểm bất kì như sau:
+ Với điểm M ta có thể nối với các điểm: N, P, Q, K để tạo thành 4 đường thẳng phân biệt.
+ Với điểm N ta có thể nối với các điểm: P, Q, K để tạo thành 3 đường thẳng phân biệt.
+ Với điểm P ta có thể nối với các điểm: Q, K để tạo thành 2 đường thẳng phân biệt.
+ Với điểm Q ta có thể nối với điểm K để tạo thành 1 đường thẳng .
Vậy từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được tất cả:
4 + 3 + 2 + 1 = 10 đường thẳng phân biệt.
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
$15$
$16$
$14$
$13$
Đáp án : A
Vì qua hai điểm phân biệt ta luôn vẽ được một đoạn thẳng nên ta tính số đoạn thẳng tạo thành từ n điểm phân biệt theo công thức: \(\dfrac{{n\left( {n - 1} \right)}}{2}\,\,\left( {n \ge 2} \right)\) đoạn thẳng
Vì qua 2 điểm luôn vẽ được một đoạn thẳng Nên qua 6 điểm vẽ được số đoạn thẳng là: \(\dfrac{{6\left( {6 - 1} \right)}}{2} = 15\) (đoạn thẳng)
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
\(276\)
\(290\)
\(262\)
\(226\)
Đáp án : C
Ta sử dụng công thức tính số đường thẳng tạo bởi n điểm phân biệt \(\left( {n \ge 2} \right)\) trong đó không có ba điểm nào thảng hàng: \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Giả sử 24 điểm không có 3 điểm nào thẳng hàng. Tính số đường thẳng vẽ được qua 24 điểm + Tính số đường thẳng vẽ được qua 6 điểm (giả sử 6 điểm không có 3 điểm nào thẳng hàng)
+ Số đường thẳng vẽ được qua 6 điểm thẳng hàng+ Tính số đường thẳng vẽ được qua 24 điểm trong đó có 6 điểm thẳng hàng
Giả sử trong 24 điểm không có 3 điểm nào thẳng hàng tất cả vẽ được: $\dfrac{{24.(24 - 1)}}{2} = 276$ (đường thẳng) Qua 6 điểm thẳng hàng vẽ được số đường thẳng là: $\dfrac{{6.(6 - 1)}}{2} = 15$ (đường thẳng) Nhưng qua 6 điểm thẳng hàng chỉ vẽ được một đường thẳng Nên qua 24 điểm trong đó có 6 điểm thẳng hàng vẽ được: $276 - 15 + 1 = 262$ (đường thẳng)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.
\(MO = 4cm\)
\(MO = 3cm\)
\(MO = 1cm\)
\(MO = 2cm\)
Đáp án: C
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.

+) Vì \(M \in AB\) nên M nằm giữa A và B
\( \Rightarrow AM + MB = AB \Rightarrow BM \)\(= AB - MB = 6 - 4 = 2cm.\)
+) Vì O là trung điểm của AB nên: \(AO = OB = \dfrac{{AB}}{2} \)\(= \dfrac{6}{2} = 3cm\)
Vì \(O \in AB\), \(M \in AB\) và \(AO < AM (3cm < 4cm)\) nên O nằm giữa A và M suy ra:
\(AO + OM = AM \Rightarrow OM\)\( = AM - AO = 4 - 3 = 1cm\)
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
Điểm I là trung điểm của OM
Điểm O nằm giữa I và P
\(IP = 2cm\)
Cả A, B, C đều đúng.
Đáp án: D
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.

+ ) Vì \(O \in AB\), \(I \in AB\) và AO < AI (3cm < 3,5cm) nên O nằm giữa A và I suy ra:
\(AO + OI = AI \)\(\Rightarrow OI = AI - AO = 3,5 - 3 = 0,5cm\) (1)
Vì \(I \in AB\), \(M \in AB\) và AI < AM (3,5cm < 4cm) nên I nằm giữa A và M suy ra:
\(AI + IM = AM \Rightarrow IM = AM - AI = 4 - 3,5 = 0,5cm\)(2)
Từ (1) và (2) suy ra $OI = IM$ . (3)
Vì O nằm giữa A và I nên A và O nằm cùng phía đối với I . Mà I nằm giữa A và M nên A và M nằm khác phía đối với I \( \Rightarrow \) O và M nằm khác phía đối với I suy ra I nằm giữa M và O (4)
Từ (3) và (4) suy ra I là trung điểm của OM.
+) Vì P là trung điểm của AO nên: \(OP = AP = \dfrac{{AO}}{2} = \dfrac{3}{2} = 1,5cm\)
Vì $\left\{ \begin{array}{l}O,M \in AB\\AO < AM\left( {3cm < 4cm} \right)\end{array} \right. \Rightarrow $ O nằm giữa A và M
Suy ra A và M nằm khác phía đối với O
Vì P là trung điểm của AO nên A, P cùng phía đối với O.
Vì I là trung điểm của OM nên I, M cùng phía đối với O.
Từ đó suy ra I nằm giữa O và P \( \Rightarrow OP + IO = IP \)\(\Rightarrow IP = 1,5 + 0,5 = 2cm\)
Em hãy chọn phát biểu sai trong các phát biểu sau:
Góc bẹt là góc có hai cạnh là hai tia đối nhau
\(\widehat A\) được gọi là góc tù nếu \(\widehat A > {90^0}\)
Nếu tia Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Tam giác $MNP$ là hình gồm các đoạn thẳng $MN, MP$ và $NP$ khi ba điểm $M, N, P$ không thẳng hàng.
Đáp án : B
Áp dụng các kiến thức về: số đo góc, tia phân giác, tam giác.
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau (đúng loại A)
+ \(\widehat A\) được gọi là góc tù nếu \(\widehat A > {90^0}\) (sai vì \(\widehat A\) được gọi là góc tù nếu \({90^0} < \widehat A < {180^0}\), chọn B)
+ Nếu tia Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)(đúng loại C)
+ Tam giác MNP là hình gồm các đoạn thẳng MN, MP và NP khi ba điểm M, N, P không thẳng hàng. (đúng loại D)
Cho ba điểm không thẳng hàng $O, A, B.$ Tia $Ox$ nằm giữa hai tia $OA, OB$ khi và chỉ khi tia $Ox$ cắt
Đoạn thẳng $AB$
Đường thẳng $AB$
Tia $AB$
Tia $BA$
Đáp án : A

Tia $Ox$ nằm giữa hai tia $OA$ và $OB$ khi tia $Ox$ cắt đoạn thẳng $AB$
Cho \(100\) tia gồm \(O{x_2},O{x_3},....,O{x_{99}}\) nằm giữa hai tia \(O{x_1}\) và \(O{x_{100}}\). Hỏi có bao nhiêu góc được tạo thành?
\(9702\) góc
\(4553\) góc
\(4950\) góc
\(4851\) góc
Đáp án : C
Áp dụng định nghĩa góc, tính chất của dãy số cách đều.
- \(O{x_1}\) cùng với các tia \(O{x_2},O{x_3},....,O{x_{100}}\) tạo thành \(99\) góc.
- \(O{x_2}\) cùng với các tia \(O{x_3},....,O{x_{100}}\) tạo thành 98 góc.
- \(O{x_3}\) cùng với các tia \(O{x_4},O{x_5},....,O{x_{100}}\) tạo thành \(97\)góc.
…………
\(O{x_{99}}\) cùng tia \(O{x_{100}}\) tạo thành 1 góc.
Vậy ta có tất cả: \(1 + 2 + 3 + ... + 99 = \dfrac{{100.99}}{2} = 4950\) góc.
Chương VI Toán 6 Cánh Diều tập trung vào các kiến thức về phân số, số thập phân và các phép toán liên quan. Bài tập cuối chương là cơ hội để học sinh hệ thống lại toàn bộ kiến thức đã học, rèn luyện kỹ năng giải toán và chuẩn bị cho các bài kiểm tra sắp tới.
Để giải các bài tập trong Bài tập cuối chương VI Toán 6 Cánh Diều, học sinh cần nắm vững các kiến thức cơ bản về phân số, số thập phân và các phép toán. Dưới đây là một số hướng dẫn cụ thể:
Để rút gọn phân số về dạng tối giản, ta chia cả tử số và mẫu số cho ước chung lớn nhất của chúng. Ví dụ, phân số 12/18 có thể được rút gọn thành 2/3 bằng cách chia cả tử số và mẫu số cho 6.
Có nhiều phương pháp để so sánh phân số, bao gồm:
Để cộng hoặc trừ hai phân số, ta cần quy đồng mẫu số trước. Sau đó, cộng hoặc trừ các tử số và giữ nguyên mẫu số. Ví dụ, 1/2 + 1/3 = 3/6 + 2/6 = 5/6.
Để nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu số với nhau. Để chia hai phân số, ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai. Ví dụ, (1/2) * (2/3) = 1/3 và (1/2) / (2/3) = (1/2) * (3/2) = 3/4.
Để chuyển đổi giữa phân số và số thập phân, ta có thể chia tử số cho mẫu số. Ví dụ, 1/4 = 0.25. Khi thực hiện các phép toán với số thập phân, ta cần chú ý đến vị trí của dấu phẩy.
Để đạt kết quả tốt trong các bài kiểm tra Toán 6, học sinh cần luyện tập thường xuyên và nắm vững các kiến thức cơ bản. Hãy sử dụng các bài tập trắc nghiệm và tự luận trên giaitoan.edu.vn để rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Bài tập cuối chương VI Toán 6 Cánh Diều là một phần quan trọng trong quá trình học tập của học sinh. Bằng cách nắm vững kiến thức, rèn luyện kỹ năng và luyện tập thường xuyên, các em sẽ đạt được kết quả tốt nhất trong môn Toán.