Đề thi giữa kì 1 Toán 6 - Đề số 17 là một công cụ ôn tập vô cùng hữu ích dành cho các em học sinh. Đề thi được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp đề thi giữa kì 1 Toán 6 - Đề số 17 kèm theo đáp án chi tiết, giúp các em tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Tập hợp \({\mathbb{N}^*}\) được biểu diễn bằng?
\(\left\{ {0;1;2;3;4;5.........} \right\}\).
\(\left\{ {0,1,2,3,4,5.........} \right\}\).
\(\left\{ {1,2,3,4,5.........} \right\}\).
\(\left\{ {1;2;3;4;5.........} \right\}\).
Tìm x biết: \(178 - x:3 = 164\). Khi đó x bằng
1026.
42.
114.
14.
Kết quả phép tính \({9^7}:{9^3}\) bằng
\({9^5}\).
\({9^4}\).
\({9^7}\).
\({9^0}\).
Kết quả phép tính \({4.5^2} - 81:{3^2}\) bằng
31.
90.
30.
91.
Công thức nào sau đây biểu diễn phép nhân hai lũy thừa cùng cơ số?
\({a^m}.{a^n} = {a^{m + n}}\).
\({a^m}:{a^n} = {a^{m + n}}\).
\({a^m}.{a^n} = {\rm{ }}{a^{m - n}}\).
\({a^m}:{a^n} = {\rm{ }}{a^{m - n}}\).
Nếu x là số tự nhiên sao cho \({\left( {x - 1} \right)^2} = 16\) thì x bằng
1.
4.
5.
17.
Số 600 phân tích ra thừa số nguyên tố là
\({2^3}{.3.5^2}\).
\({2^4}{.3.5^2}\).
\({2^3}.3.5\).
\({2^4}{.5^2}{.3^2}\).
Biểu thức 2.3.5 + 35 chia hết cho số nào sau đây?
2.
3.
5.
7.
Trong các tập hợp sau, tập hợp nào có các phần tử đều là số nguyên tố
\(\left\{ {1;\,3;\,\,4;\,\,5;\,\,7} \right\}\).
\(\left\{ {1;2;\,\,3;\,\,\,5;\,\,7} \right\}\).
\(\left\{ {2;\,\,13;\,\,5;\,\,27} \right\}\).
\(\left\{ {2;\,\,13;\,\,5;\,\,29} \right\}\).
Hãy chọn câu sai. Trong hình chữ nhật có:
Hai cạnh đối bằng nhau.
Hai đường chéo bằng nhau.
Bốn cạnh bằng nhau.
Hai cạnh đối song song với nhau.
Cho một hình vuông, hỏi nếu cạnh của hình vuông đã cho tăng gấp 3 lần thì diện tích của nó tăng gấp bao nhiêu lần?
3.
6.
8.
9.
Một hình thoi có diện tích bằng 24 cm2. Biết độ dài một đường chéo bằng 6 cm, tính độ dài đường chéo còn lại của hình thoi đó.
4 cm.
8 cm.
12 cm.
16 cm.
Thực hiện phép tính (tính nhanh nếu có thể)
a) \(146 + 121 + 54 + 379\)
b) \({2^3}.17-{2^3}.14\)
c) \({5^{19}}:{5^{17}} + {3.3^3}-{7^0}\)
d) \(50-\left[ {\left( {20-{2^3}} \right):2} \right]\)
Tìm số tự nhiên x, biết
a) \(5.{\rm{x}} - 13 = 102\)
b) \(21 + {3^{{\rm{x}} - 2}} = 48\)
c) \(2.x-14 = {5.2^3}\)
Tìm các chữ số a, b để: Số \(\overline {4a12b} \) chia hết cho cả 2; 5 và 9.
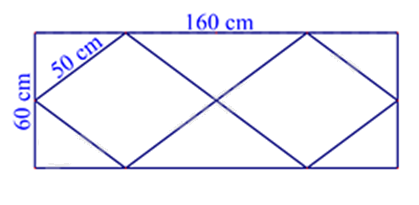
Một người thợ làm khung thép cho ô thoáng khí cửa ra vào có kích thước và hình dạng như hình vẽ dưới đây. Khung thép bên ngoài là một hình chữ nhật có chiều dài \(160\,{\rm{cm}}\) và chiều rộng \(60\,{\rm{cm}}\). Phía trong là hai hình thoi cạnh \(50\,{\rm{cm}}\). Hỏi chiều dài của thanh thép ban đầu là bao nhiêu, biết sau khi làm xong khung thép thì thanh thép còn dư 10cm? (Coi như các mối hàn không đáng kể).
Cho \(B = 3 + {3^2} + {3^3} + ... + {3^{100}}\)
Tìm số tự nhiên n, biết rằng \(2B + 3 = {3^n}\)
Tập hợp \({\mathbb{N}^*}\) được biểu diễn bằng?
\(\left\{ {0;1;2;3;4;5.........} \right\}\).
\(\left\{ {0,1,2,3,4,5.........} \right\}\).
\(\left\{ {1,2,3,4,5.........} \right\}\).
\(\left\{ {1;2;3;4;5.........} \right\}\).
Đáp án : D
Dựa vào kiến thức về tập hợp số tự nhiên.
Tập \({\mathbb{N}^*} = \left\{ {1;2;3;4;5.........} \right\}\).
Các số phải cách nhau bởi dấu “;”.
Đáp án D.
Tìm x biết: \(178 - x:3 = 164\). Khi đó x bằng
1026.
42.
114.
14.
Đáp án : A
Dựa vào quy tắc chuyển vế để tìm x.
Ta có:
\(\begin{array}{l}178 - x:3 = 164\\x:3 = 178 + 164\\x:3 = 342\\x = 342.3\\x = 1026\end{array}\)
Vậy \(x = 1026\).
Đáp án A.
Kết quả phép tính \({9^7}:{9^3}\) bằng
\({9^5}\).
\({9^4}\).
\({9^7}\).
\({9^0}\).
Đáp án : B
Dựa vào kiến thức chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0;m \ge n \ge 0} \right)\).
\({9^7}:{9^3} = {9^{7 - 3}} = {9^4}\).
Đáp án B.
Kết quả phép tính \({4.5^2} - 81:{3^2}\) bằng
31.
90.
30.
91.
Đáp án : D
Nếu phép tính có cả cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.
\({4.5^2} - 81:{3^2} = 4.25 - 81:9 = 100 - 9 = 91\)
Đáp án D.
Công thức nào sau đây biểu diễn phép nhân hai lũy thừa cùng cơ số?
\({a^m}.{a^n} = {a^{m + n}}\).
\({a^m}:{a^n} = {a^{m + n}}\).
\({a^m}.{a^n} = {\rm{ }}{a^{m - n}}\).
\({a^m}:{a^n} = {\rm{ }}{a^{m - n}}\).
Đáp án : A
Nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\).
Công thức biểu diễn phép nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\).
Đáp án A.
Nếu x là số tự nhiên sao cho \({\left( {x - 1} \right)^2} = 16\) thì x bằng
1.
4.
5.
17.
Đáp án : C
Sử dụng kiến thức về lũy thừa.
\({\left( {x - 1} \right)^2} = 16\)
\({\left( {x - 1} \right)^2} = {4^2}\)
\(x - 1 = 4\)
\(x = 4 + 1\)
\(x = 5\)
Vậy \(x = 5\).
Đáp án C.
Số 600 phân tích ra thừa số nguyên tố là
\({2^3}{.3.5^2}\).
\({2^4}{.3.5^2}\).
\({2^3}.3.5\).
\({2^4}{.5^2}{.3^2}\).
Đáp án : A
Phân tích một số ra thừa số nguyên tố bằng sơ đồ cây hoặc sơ đồ cột.

Vậy \(600 = {2^3}{.3.5^2}\).
Đáp án A.
Biểu thức 2.3.5 + 35 chia hết cho số nào sau đây?
2.
3.
5.
7.
Đáp án : C
Dựa vào tính chất chia hết của một tổng.
Vì \(\left( {2.3.5} \right) \vdots 5\) và \(35 \vdots 5\) nên \(\left( {2.3.5 + 35} \right) \vdots 5\).
Đáp án C.
Trong các tập hợp sau, tập hợp nào có các phần tử đều là số nguyên tố
\(\left\{ {1;\,3;\,\,4;\,\,5;\,\,7} \right\}\).
\(\left\{ {1;2;\,\,3;\,\,\,5;\,\,7} \right\}\).
\(\left\{ {2;\,\,13;\,\,5;\,\,27} \right\}\).
\(\left\{ {2;\,\,13;\,\,5;\,\,29} \right\}\).
Đáp án : D
Dựa vào kiến thức về số nguyên tố.
\(\left\{ {1;\,3;\,\,4;\,\,5;\,\,7} \right\}\) có 1 và 4 không phải số nguyên tố.
\(\left\{ {1;2;\,\,3;\,\,\,5;\,\,7} \right\}\) có 1 không phải số nguyên tố.
\(\left\{ {2;\,\,13;\,\,5;\,\,27} \right\}\) có 27 không phải số nguyên tố.
Vì 2; 5; 13; 29 đều là số nguyên tố nên \(\left\{ {2;\,\,13;\,\,5;\,\,29} \right\}\) có tất cả phần tử đều là số nguyên tố.
Đáp án D.
Hãy chọn câu sai. Trong hình chữ nhật có:
Hai cạnh đối bằng nhau.
Hai đường chéo bằng nhau.
Bốn cạnh bằng nhau.
Hai cạnh đối song song với nhau.
Đáp án : C
Dựa vào đặc điểm của hình chữ nhật:
- Các cạnh đối bằng nhau.
- Hai đường chéo bằng nhau.
Hình chữ nhật có hai cạnh đối song song và bằng nhau nên A, D đúng.
Hình chữ nhật có hai đường chéo bằng nhau nên B đúng.
Hình chữ nhật không có bốn cạnh bằng nhau nên C sai.
Đáp án C.
Cho một hình vuông, hỏi nếu cạnh của hình vuông đã cho tăng gấp 3 lần thì diện tích của nó tăng gấp bao nhiêu lần?
3.
6.
8.
9.
Đáp án : D
Sử dụng công thức tính diện tích hình vuông: S = cạnh . cạnh.
Giả sử cạnh hình vuông ban đầu là \(x\). Khi đó diện tích hình vuông là \(x.x = {x^2}\).
Nếu cạnh hình vuông tăng gấp 3 lần thì cạnh mới là \(3x\), khi đó diện tích hình vuông mới là \(3x.3x = 9{x^2}\).
Diện tích của nó tăng gấp số lần là 9 lần.
Đáp án D.
Một hình thoi có diện tích bằng 24 cm2. Biết độ dài một đường chéo bằng 6 cm, tính độ dài đường chéo còn lại của hình thoi đó.
4 cm.
8 cm.
12 cm.
16 cm.
Đáp án : B
Dựa vào công thức tính diện tích hình thoi bằng \(\frac{1}{2}\) tích hai đường chéo để tính đường chéo còn lại.
Độ dài đường chéo còn lại của hình thoi là:
\(S = 24.2:6 = 8\left( {cm} \right)\)
Đáp án B.
Thực hiện phép tính (tính nhanh nếu có thể)
a) \(146 + 121 + 54 + 379\)
b) \({2^3}.17-{2^3}.14\)
c) \({5^{19}}:{5^{17}} + {3.3^3}-{7^0}\)
d) \(50-\left[ {\left( {20-{2^3}} \right):2} \right]\)
Sử dụng tính chất của phép tính với số tự nhiên.
Nếu phép tính có cả cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.
Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
a) \(146 + 121 + 54 + 379\)
\(\begin{array}{l} = \left( {146 + 54} \right) + \left( {121\; + 379} \right)\\ = 200 + 500\\ = 700\end{array}\)
b) \({2^3}.17-{2^3}.14\)
\(\begin{array}{l} = {2^3}.\left( {17 - 14} \right)\\ = 8.3\\ = 24\end{array}\)
c) \({5^{19}}:{5^{17}} + {3.3^3}-{7^0}\)
\(\begin{array}{*{20}{l}}{ = {5^2} + {3^4}-1}\\\begin{array}{l} = \;25 + 81 - 1\\ = 105\end{array}\end{array}\)
d) \(50-\left[ {\left( {20-{2^3}} \right):2} \right]\)
\(\begin{array}{l} = 50-\left( {12:2} \right)\\ = 44\end{array}\)
Tìm số tự nhiên x, biết
a) \(5.{\rm{x}} - 13 = 102\)
b) \(21 + {3^{{\rm{x}} - 2}} = 48\)
c) \(2.x-14 = {5.2^3}\)
Sử dụng quy tắc chuyển vế kết hợp với các phép tính để tìm x.
a) \(5.{\rm{x}} - 13 = 102\)
\(\begin{array}{*{20}{l}}{5.x = 102 + 13}\\{5.x = {\rm{ }}115}\\{x = 115:5}\\{x = 23}\end{array}\)
Vậy \(x = 23\).
b) \(21 + {3^{{\rm{x}} - 2}} = 48\)
\(\begin{array}{l}{3^{x - 2}} = 48 - 21\\{3^{x - 2}} = 27\\{3^{x - 2}} = {3^3}\\x - 2 = 3\\x = 3 + 2\\x = 5\end{array}\)
Vậy \(x = 5\)
c) \(2.x-14 = {5.2^3}\)
\(\begin{array}{*{20}{l}}{2.x - 14 = 40}\\{2.x = 40 + 14}\\{2.x = 54}\\{x = 54:2}\\{x = 27}\end{array}\)
Vậy \(x = 27\)
Tìm các chữ số a, b để: Số \(\overline {4a12b} \) chia hết cho cả 2; 5 và 9.
Dựa vào dấu hiệu chia hết của 2; 5; 9.
Vì \(\overline {4a12b} \) chia hết cho cả 2; 5 nên chữ số tận cùng là 0 hay \(b = 0\).
Vì \(\overline {4a120} \) chia hết cho 9 nên \(4 + a + 1 + 2 + 0 = \left( {7 + a} \right)\; \vdots 9\).
Mà \(0 \le a \le 9\) nên \(7 + a\) chỉ có thể bằng 9.
Suy ra \(a = 9 - 7 = 2\)
Vậy \(a = 2;b = 0\).
Một người thợ làm khung thép cho ô thoáng khí cửa ra vào có kích thước và hình dạng như hình vẽ dưới đây. Khung thép bên ngoài là một hình chữ nhật có chiều dài \(160\,{\rm{cm}}\) và chiều rộng \(60\,{\rm{cm}}\). Phía trong là hai hình thoi cạnh \(50\,{\rm{cm}}\). Hỏi chiều dài của thanh thép ban đầu là bao nhiêu, biết sau khi làm xong khung thép thì thanh thép còn dư 10cm? (Coi như các mối hàn không đáng kể).
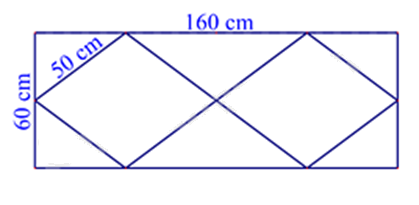
Sử dụng công thức tính chu vi hình chữ nhật, chu vi hình thoi.
Chu vi hình chữ nhật = 2. (chiều dài + chiều rộng).
Chu vi hình thoi = 4. cạnh.
Chu vi hình chữ nhật là:
\(2.(160 + 60) = 440(cm)\)
Chu vi hình thoi là
\(4.50.2 = 400(cm)\)
Tổng chiều dài thanh thép là:
\(440 + 400 + 10 = 850(cm)\)
Đổi 850 cm = 8,5 m.
Vậy chiều dài thanh thép ban đầu là 8,5 mét.
Cho \(B = 3 + {3^2} + {3^3} + ... + {3^{100}}\)
Tìm số tự nhiên n, biết rằng \(2B + 3 = {3^n}\)
Từ B tính \(3B\).
Thực hiện phép tính \(3B - B\) để có \(2B\).
Cộng 3, ta được \(2B + 3\).
Mà \(2B + 3 = {3^n}\) nên ta tính được n.
Ta có: \(B\;\; = 3 + {3^2} + {3^3} + ... + {3^{99}} + {3^{100}}\)
Suy ra \(3B\; = {3^2} + {3^3} + ... + {3^{100}} + {3^{101}}\)
Lấy 3B trừ B ta được:
\(\begin{array}{l}3B\; - B\; = {3^2} + {3^3} + ... + {3^{100}} + {3^{101}} - \left( {3 + {3^2} + {3^3} + ... + {3^{99}} + {3^{100}}} \right)\\2B = {3^{101}} - 3\end{array}\)
Do đó: \(2B + 3 = {3^{101}}\).
Theo đề bài \(2B + 3 = {3^n}\) nên \(n = 101\).
Vậy \(n = 101\).
Đề thi giữa kì 1 Toán 6 - Đề số 17 thường bao gồm các dạng bài tập thuộc các chủ đề chính đã học trong nửa học kì đầu tiên. Các chủ đề này thường bao gồm:
Cấu trúc đề thi thường bao gồm phần trắc nghiệm (5-7 câu) và phần tự luận (3-5 câu). Các câu hỏi tự luận thường yêu cầu học sinh trình bày lời giải chi tiết, rõ ràng.
Để giúp học sinh ôn tập hiệu quả, giaitoan.edu.vn cung cấp đáp án chi tiết và lời giải cho từng câu hỏi trong Đề thi giữa kì 1 Toán 6 - Đề số 17. Dưới đây là một số gợi ý giải bài tập:
Khi thực hiện các phép tính, cần chú ý thứ tự thực hiện các phép toán (nhân, chia trước; cộng, trừ sau). Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Để tìm x, cần thực hiện các phép toán ngược lại với các phép toán đã cho. Ví dụ, nếu x + 5 = 10, thì x = 10 - 5 = 5.
Khi giải bài toán có lời văn, cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Sau đó, cần xác định các dữ kiện đã cho và các đại lượng cần tìm. Cuối cùng, cần lập phương trình hoặc biểu thức để giải bài toán.
Việc luyện tập với Đề thi giữa kì 1 Toán 6 - Đề số 17 mang lại nhiều lợi ích cho học sinh:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 6, học sinh cần có phương pháp ôn tập hiệu quả:
Ngoài Đề thi giữa kì 1 Toán 6 - Đề số 17, học sinh có thể tham khảo thêm các tài liệu sau:
Đề thi giữa kì 1 Toán 6 - Đề số 17 là một công cụ hỗ trợ học tập vô cùng hữu ích. Hy vọng rằng, với những hướng dẫn và gợi ý trên, các em học sinh sẽ ôn tập hiệu quả và đạt kết quả tốt trong kỳ thi sắp tới. Chúc các em thành công!