Chào mừng các em học sinh lớp 6 đến với đề thi học kì 2 môn Toán số 8 của giaitoan.edu.vn. Đề thi này được biên soạn dựa trên chương trình học Toán 6, bao gồm các dạng bài tập thường gặp trong đề thi chính thức.
Mục tiêu của đề thi này là giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự đánh giá năng lực của bản thân trước kỳ thi quan trọng.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. D | 2. B | 3. B | 4. D |
Câu 1
Phương pháp:
Tính khối lượng của bao thứ hai, bao thứ ba, từ đó tính được khối lượng của ba bao đường.
Cách giải:
Bao thứ hai nặng: \(37,6 + 22,4 = 60\left( {kg} \right)\)
Bao thứ ba nặng: \(\dfrac{3}{5}.60 = 36\left( {kg} \right)\)
Cả ba bao đường nặng: \(37,6 + 60 + 36 = 133,6\left( {kg} \right)\)
Chọn D.
Câu 2
Phương pháp:
Áp dụng công thức tính xác suất thực nghiệm: \(\dfrac{{n(A)}}{n}\)
+ Bước 1: Xác định số lần không lấy được sách Tiếng Việt.
+ Bước 2: Tính xác suất thực nghiệm.
Cách giải:
Số lần không lấy được sách Tiếng Việt là: \(14 + 16 = 30\) (lần)
Xác suất thực nghiệm của sự kiện “ Không lấy được sách Tiếng Việt” là: \(\dfrac{{30}}{{40}} = 0,75\)
Chọn B.
Câu 3
Phương pháp:
Sử dụng khái niệm ba điểm thẳng hàng
Cách giải:
Có \(4\) bộ ba điểm thẳng hàng: \(\left( {A,E,B} \right);\left( {F;E,D,} \right);\left( {F,B,C} \right);\left( {A,D,C} \right)\)
Chọn B.
Câu 4
Phương pháp:
Dựa vào tính chất của các góc.
Cách giải:
- Góc lớn hơn góc vuông là góc tù hoặc góc bẹt.
- Góc nhỏ hơn góc bẹt là góc tù, góc vuông hoặc góc nhọn.
- Góc lớn hơn góc nhọn là góc tù, góc vuông hoặc góc bẹt.
- Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp:
Tính giá trị biểu thức theo các quy tắc:
- Biểu thức có dấu ngoặc thì ưu tiên tính trong ngoặc trước, ngoài ngoặc sau.
- Biểu thức có chứa các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, phép tính cộng, trừ sau.
Cách giải:
a) \(\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\)
\( = \left( {\dfrac{{ - 10}}{{13}} + \dfrac{{ - 3}}{{13}}} \right) + \left( {\dfrac{5}{{17}} + \dfrac{{12}}{{17}}} \right) - \dfrac{{11}}{{20}}\)
\( = \dfrac{{ - 13}}{{13}} + \dfrac{{17}}{{17}} - \dfrac{{11}}{{20}}\)
\(= ( - 1) + 1 - \dfrac{{11}}{{20}}\)
\( = 0 - \dfrac{{11}}{{20}}= {\rm{\;}} - \dfrac{{11}}{{20}}\)
b) \(\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}}\)
\( = \dfrac{3}{4} + \dfrac{{ - 5}}{6} + \dfrac{{11}}{{12}}\)
\( = \dfrac{9}{{12}}+ \dfrac{{ - 10}}{{12}} + \dfrac{{11}}{{12}}\)
\( = \dfrac{{9 + ( - 10) + 11}}{{12}}\)
\( = \dfrac{{10}}{{12}} = \dfrac{5}{6}\)
c) \(\left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}\)
\( = \,\left( {13 + \dfrac{4}{9} + 2 + \dfrac{1}{9}} \right) - \left( {3 + \dfrac{4}{9}} \right)\)
\( = 13 + \dfrac{4}{9} + 2 + \dfrac{1}{9} - 3 - \dfrac{4}{9}\)
\( = (13 + 2 - 3) + \left( {\dfrac{4}{9} - \dfrac{4}{9}} \right) + \dfrac{1}{9}\)
\( = 12 + 0 + \dfrac{1}{9}= 12\dfrac{1}{9}\)
d) \(1,25:\dfrac{{15}}{{20}} + \left( {25\% {\rm{\;}} - \dfrac{5}{6}} \right):4\dfrac{2}{3}\)
\( = \dfrac{5}{4}:\dfrac{3}{4} + \left( {\dfrac{1}{4} - \dfrac{5}{6}} \right):\dfrac{{14}}{3}\)
\( = \dfrac{5}{4}.\dfrac{4}{3} + \left( {\dfrac{3}{{12}} - \dfrac{{10}}{{12}}} \right).\dfrac{3}{{14}}\)
\( = \dfrac{5}{3} + \dfrac{{ - 7}}{{12}}.\dfrac{3}{{14}}\)
\( = \dfrac{5}{3} + \dfrac{{ - 1}}{8} = \dfrac{{40}}{{24}} + \dfrac{{ - 3}}{{24}}= \dfrac{{37}}{{24}}\)
Bài 2
Phương pháp:
Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Cách giải:
a) \(\dfrac{{29}}{4}x - \dfrac{7}{6} = \dfrac{5}{4}\)
\(\dfrac{{29}}{4}x = \dfrac{5}{4} + \dfrac{7}{6}\)
\(\dfrac{{29}}{4}x = \dfrac{{29}}{{12}}\)
\(x = \dfrac{{29}}{{12}}:\dfrac{{29}}{4}\)
\(x = \dfrac{1}{3}\)
Vậy \(x = \dfrac{1}{3}\).
b) \(2\dfrac{3}{5}:\left( {6x - \dfrac{1}{2}} \right) = \dfrac{{13}}{{10}}\)
\(\dfrac{{13}}{5}:\left( {6x - \dfrac{1}{2}} \right) = \dfrac{{13}}{{10}}\)
\(6x - \dfrac{1}{2} = \dfrac{{13}}{5}:\dfrac{{13}}{{10}}\)
\(6x - \dfrac{1}{2} = 2\)
\(6x = 2 + \dfrac{1}{2}\)
\(6x = \dfrac{5}{2}\)
\(x = \dfrac{5}{2}:6\)
\(x = \dfrac{5}{{12}}\)
Vậy \(x = \dfrac{5}{{12}}\).
c) \(\dfrac{1}{3}.\left( {3x - 2} \right) + 25\% = - \dfrac{9}{6}\)
\(\dfrac{1}{3}\left( {3x - 2} \right) + \dfrac{1}{4} = - \dfrac{3}{2}\)
\(\dfrac{1}{3}\left( {3x - 2} \right) = - \dfrac{3}{2} - \dfrac{1}{4}\)
\(\dfrac{1}{3}\left( {3x - 2} \right) = \dfrac{{ - 7}}{4}\)
\(3x - 2 = \dfrac{{ - 7}}{4}:\dfrac{1}{3}\)
\(3x - 2 = \dfrac{{ - 21}}{4}\)
\(3x = \dfrac{{ - 21}}{4} + 2\)
\(3x = \dfrac{{ - 13}}{4}\)
\(x = \dfrac{{ - 13}}{4}:3\)
\(x = \dfrac{{ - 13}}{{12}}\)
Vậy \(x = \dfrac{{ - 13}}{{12}}\).
Bài 3
Phương pháp:
a) Quy tắc tìm giá trị phân số của một số cho trước: Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\left( {m,n \in \mathbb{N},n \ne 0} \right).\)
b) Quy tắc tìm một số khi biết giá trị phân số của nó: Muốn tìm một số biết \(\dfrac{m}{n}\) của nó bằng \(a\), ta tính \(a:\dfrac{m}{n}\left( {m,n \in {\mathbb{N}^*}} \right)\). Cách giải:
a) Đổi \(80\% {\rm{\;}} = \dfrac{4}{5}\).
Phân số chỉ số học sinh đạt giải ba so với số học sinh đạt giải nhất là: \(1 - \dfrac{4}{5} = \dfrac{1}{5}\) (số học sinh đạt giải nhất)
Số học sinh đạt giải nhất là: \(5:\dfrac{1}{5} = 25\) (học sinh)
Tổng số học sinh của đoàn đó là: \(25:\dfrac{1}{2} = 50\) (học sinh)
b) Theo câu ta có số học sinh đạt giải nhất là 25 học sinh.
Số học sinh đạt giải nhì là: \(25.80\% {\rm{\;}} = 20\) (học sinh)
Tỉ số phần trăm số học sinh đạt giải nhất so với tổng số học sinh đi thi là: \(25:50.100\% {\rm{\;}} = 50\% \)
Tỉ số phần trăm số học sinh đạt giải nhì so với tổng số học sinh đi thi là: \(20:50.100\% {\rm{\;}} = 40\% \)
Tỉ số phần trăm số học sinh đạt giải ba so với tổng số học sinh đi thi là: \(5:50.100\% {\rm{\;}} = 10\% \)
Bài 4
Phương pháp:
Dựa vào dấu hiệu nhận biết một điểm nằm giữa hai điểm và tính chất trung điểm của đoạn thẳng.
Cách giải:

a) Trên tia Ax ta có \(AM < AB\left( {4cm < 8cm} \right)\) suy ra điểm \(M\) nằm giữa hai điểm \(A\) và \(B\).
b) Theo câu a, điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) nên ta có: \(AM + MB = AB\)\( \Rightarrow MB = AB - AM = 8 - 4 = 4cm\)
Vậy \(AM = MB = 4cm\).
c) Theo câu a và b ta có: \(M\) nằm giữa hai điểm \(A\) và \(B\) và \(MA = MB\).
Vậy \(M\) là trung điểm của đoạn thẳng AB.
b) Trên tia Ax ta có \(AB < AN\left( {8cm < 12cm} \right)\) suy ra điểm B nằm giữa hai điểm A và N
\(\begin{array}{*{20}{l}}{ \Rightarrow AB + BN = AN}\\{ \Rightarrow BN = AN - AB = 12 - 8 = 4cm}\end{array}\)
Vậy \(MB = \;BN = 4cm\).
Bài 5
Phương pháp:
Phân tích \(A = a + \dfrac{b}{{3 - n}}\), với \(a,\,\,b \in \mathbb{Z}\).
Để \(A \in \mathbb{Z}\) thì \(3 - n \in U\left( b \right)\).
Cách giải:
\(\begin{array}{l}A = \dfrac{{2n - 1}}{{3 - n}} = \dfrac{{2n - 6 + 5}}{{ - n + 3}}\\\,\,\,\,\, = \dfrac{{2n - 6}}{{ - n + 3}} + \dfrac{5}{{ - n + 3}}\\\,\,\,\,\, = \dfrac{{ - 2\left( { - n + 3} \right)}}{{ - n + 3}} + \dfrac{5}{{ - n + 3}}\\\,\,\,\,\, = - 2 + \dfrac{5}{{ - n + 3}}\end{array}\)
Để A nhận giá trị nguyên thì \( - 2 + \dfrac{5}{{ - n + 3}} \in \mathbb{Z} \Rightarrow \dfrac{5}{{ - n + 3}} \in \mathbb{Z}\)\( \Rightarrow - n + 3 \in \left\{ { \pm 1; \pm 5} \right\}\)
Ta có bảng giá trị sau:

Vậy \(n \in \left\{ {2;4; - 2;8} \right\}\).
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Có ba bao đường: bao thứ nhất nặng 37,6kg; bao thứ hai nặng hơn bao thứ nhât 22,4kg; bao thứ ba nặng bằng \(\dfrac{3}{5}\) bao thứ hai. Cả ba bao đường có khối lượng là:
A. 97,6kg
B. 96kg
C. 73,6kg
D. 133,6kg
Câu 2: Trong cặp có một số quyển sách là: sách Toán, sách Tiếng Việt và sách Lịch sử. Lấy ngẫu nhiên 1 quyển từ cặp, xem là sách gì rồi trả lại. Lặp lại hoạt động đó 40 ta được kết quả như sau:

A. 0,25
B. 0,75
C. 0,1
D. 0,9
Câu 3: Số bộ ba điểm thẳng hàng trong hình vẽ dưới là:
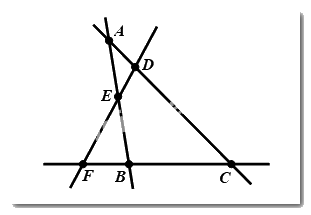
A. \(2\) bộ
B. \(4\) bộ
C. \(3\) bộ
D. \(5\) bộ
Câu 4: Câu nào đúng?
A. Góc lớn hơn góc vuông là góc tù.
B. Góc nhỏ hơn góc bẹt là góc tù.
C. Góc lớn hơn góc nhọn là góc tù.
D. Góc lớn hơn góc vuông, nhỏ hơn góc bẹt là góc tù
Phần II. Tự luận
Bài 1: Thực hiện phép tính (Tính hợp lý nếu có thể).
a) \(\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\)
b) \(\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}}\)
c) \(\left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}\)
d) \(1,25:\dfrac{{15}}{{20}} + \left( {25\% {\rm{\;}} - \dfrac{5}{6}} \right):4\dfrac{2}{3}\)
Bài 2: Tìm \(x\), biết:
a) \(\dfrac{{29}}{4}x - \dfrac{7}{6} = \dfrac{5}{4}\)
b) \(2\dfrac{3}{5}:\left( {6x - \dfrac{1}{2}} \right) = \dfrac{{13}}{{10}}\)
c) \(\dfrac{1}{3}.\left( {3x - 2} \right) + 25\% {\rm{\;}} = {\rm{\;}} - \dfrac{9}{6}\)
Bài 3: Một đoàn học sinh đi thi học sinh giỏi đều đạt giải. Trong đó số học sinh đạt giải nhất chiếm \(\dfrac{1}{2}\) tổng số học sinh; số học sinh đạt giải nhì bằng \(80\% \) số học sinh đạt giải nhất; còn lại có \(5\) học sinh đạt giải ba.
a) Tính tổng số học sinh của đoàn.
b) Tính số học sinh đạt giải nhất, giải nhì và tỉ số phần trăm số học sinh đạt giải từng loại so với tổng số học sinh đi thi.
Bài 4: Vẽ tia \(Ax\).Trên tia \(Ax\) lấy hai điểm \(M\) và \(B\) sao cho \(AM = 4cm,AB = 8cm\).
a) Điểm \(M\) có nằm giữa hai điểm \(A\) và \(B\) không? Vì sao?
b) So sánh \(MA\) và \(MB\).
c) \(M\) có là trung điểm của \(AB\) không? Vì sao?
d) Lấy điểm \(N\) thuộc tia \(Ax\) sao cho \(AN = 12cm\). So sánh \(BM\) và \(BN\).
Bài 5: Tìm các số nguyên n để biểu thức sau nhận giá trị là số nguyên: \(A = \dfrac{{2n - 1}}{{3 - n}}\).
Tải về
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Có ba bao đường: bao thứ nhất nặng 37,6kg; bao thứ hai nặng hơn bao thứ nhât 22,4kg; bao thứ ba nặng bằng \(\dfrac{3}{5}\) bao thứ hai. Cả ba bao đường có khối lượng là:
A. 97,6kg
B. 96kg
C. 73,6kg
D. 133,6kg
Câu 2: Trong cặp có một số quyển sách là: sách Toán, sách Tiếng Việt và sách Lịch sử. Lấy ngẫu nhiên 1 quyển từ cặp, xem là sách gì rồi trả lại. Lặp lại hoạt động đó 40 ta được kết quả như sau:

A. 0,25
B. 0,75
C. 0,1
D. 0,9
Câu 3: Số bộ ba điểm thẳng hàng trong hình vẽ dưới là:
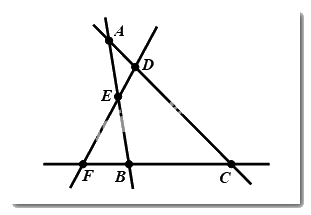
A. \(2\) bộ
B. \(4\) bộ
C. \(3\) bộ
D. \(5\) bộ
Câu 4: Câu nào đúng?
A. Góc lớn hơn góc vuông là góc tù.
B. Góc nhỏ hơn góc bẹt là góc tù.
C. Góc lớn hơn góc nhọn là góc tù.
D. Góc lớn hơn góc vuông, nhỏ hơn góc bẹt là góc tù
Phần II. Tự luận
Bài 1: Thực hiện phép tính (Tính hợp lý nếu có thể).
a) \(\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\)
b) \(\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}}\)
c) \(\left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}\)
d) \(1,25:\dfrac{{15}}{{20}} + \left( {25\% {\rm{\;}} - \dfrac{5}{6}} \right):4\dfrac{2}{3}\)
Bài 2: Tìm \(x\), biết:
a) \(\dfrac{{29}}{4}x - \dfrac{7}{6} = \dfrac{5}{4}\)
b) \(2\dfrac{3}{5}:\left( {6x - \dfrac{1}{2}} \right) = \dfrac{{13}}{{10}}\)
c) \(\dfrac{1}{3}.\left( {3x - 2} \right) + 25\% {\rm{\;}} = {\rm{\;}} - \dfrac{9}{6}\)
Bài 3: Một đoàn học sinh đi thi học sinh giỏi đều đạt giải. Trong đó số học sinh đạt giải nhất chiếm \(\dfrac{1}{2}\) tổng số học sinh; số học sinh đạt giải nhì bằng \(80\% \) số học sinh đạt giải nhất; còn lại có \(5\) học sinh đạt giải ba.
a) Tính tổng số học sinh của đoàn.
b) Tính số học sinh đạt giải nhất, giải nhì và tỉ số phần trăm số học sinh đạt giải từng loại so với tổng số học sinh đi thi.
Bài 4: Vẽ tia \(Ax\).Trên tia \(Ax\) lấy hai điểm \(M\) và \(B\) sao cho \(AM = 4cm,AB = 8cm\).
a) Điểm \(M\) có nằm giữa hai điểm \(A\) và \(B\) không? Vì sao?
b) So sánh \(MA\) và \(MB\).
c) \(M\) có là trung điểm của \(AB\) không? Vì sao?
d) Lấy điểm \(N\) thuộc tia \(Ax\) sao cho \(AN = 12cm\). So sánh \(BM\) và \(BN\).
Bài 5: Tìm các số nguyên n để biểu thức sau nhận giá trị là số nguyên: \(A = \dfrac{{2n - 1}}{{3 - n}}\).
Phần I: Trắc nghiệm
1. D | 2. B | 3. B | 4. D |
Câu 1
Phương pháp:
Tính khối lượng của bao thứ hai, bao thứ ba, từ đó tính được khối lượng của ba bao đường.
Cách giải:
Bao thứ hai nặng: \(37,6 + 22,4 = 60\left( {kg} \right)\)
Bao thứ ba nặng: \(\dfrac{3}{5}.60 = 36\left( {kg} \right)\)
Cả ba bao đường nặng: \(37,6 + 60 + 36 = 133,6\left( {kg} \right)\)
Chọn D.
Câu 2
Phương pháp:
Áp dụng công thức tính xác suất thực nghiệm: \(\dfrac{{n(A)}}{n}\)
+ Bước 1: Xác định số lần không lấy được sách Tiếng Việt.
+ Bước 2: Tính xác suất thực nghiệm.
Cách giải:
Số lần không lấy được sách Tiếng Việt là: \(14 + 16 = 30\) (lần)
Xác suất thực nghiệm của sự kiện “ Không lấy được sách Tiếng Việt” là: \(\dfrac{{30}}{{40}} = 0,75\)
Chọn B.
Câu 3
Phương pháp:
Sử dụng khái niệm ba điểm thẳng hàng
Cách giải:
Có \(4\) bộ ba điểm thẳng hàng: \(\left( {A,E,B} \right);\left( {F;E,D,} \right);\left( {F,B,C} \right);\left( {A,D,C} \right)\)
Chọn B.
Câu 4
Phương pháp:
Dựa vào tính chất của các góc.
Cách giải:
- Góc lớn hơn góc vuông là góc tù hoặc góc bẹt.
- Góc nhỏ hơn góc bẹt là góc tù, góc vuông hoặc góc nhọn.
- Góc lớn hơn góc nhọn là góc tù, góc vuông hoặc góc bẹt.
- Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp:
Tính giá trị biểu thức theo các quy tắc:
- Biểu thức có dấu ngoặc thì ưu tiên tính trong ngoặc trước, ngoài ngoặc sau.
- Biểu thức có chứa các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, phép tính cộng, trừ sau.
Cách giải:
a) \(\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\)
\( = \left( {\dfrac{{ - 10}}{{13}} + \dfrac{{ - 3}}{{13}}} \right) + \left( {\dfrac{5}{{17}} + \dfrac{{12}}{{17}}} \right) - \dfrac{{11}}{{20}}\)
\( = \dfrac{{ - 13}}{{13}} + \dfrac{{17}}{{17}} - \dfrac{{11}}{{20}}\)
\(= ( - 1) + 1 - \dfrac{{11}}{{20}}\)
\( = 0 - \dfrac{{11}}{{20}}= {\rm{\;}} - \dfrac{{11}}{{20}}\)
b) \(\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}}\)
\( = \dfrac{3}{4} + \dfrac{{ - 5}}{6} + \dfrac{{11}}{{12}}\)
\( = \dfrac{9}{{12}}+ \dfrac{{ - 10}}{{12}} + \dfrac{{11}}{{12}}\)
\( = \dfrac{{9 + ( - 10) + 11}}{{12}}\)
\( = \dfrac{{10}}{{12}} = \dfrac{5}{6}\)
c) \(\left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}\)
\( = \,\left( {13 + \dfrac{4}{9} + 2 + \dfrac{1}{9}} \right) - \left( {3 + \dfrac{4}{9}} \right)\)
\( = 13 + \dfrac{4}{9} + 2 + \dfrac{1}{9} - 3 - \dfrac{4}{9}\)
\( = (13 + 2 - 3) + \left( {\dfrac{4}{9} - \dfrac{4}{9}} \right) + \dfrac{1}{9}\)
\( = 12 + 0 + \dfrac{1}{9}= 12\dfrac{1}{9}\)
d) \(1,25:\dfrac{{15}}{{20}} + \left( {25\% {\rm{\;}} - \dfrac{5}{6}} \right):4\dfrac{2}{3}\)
\( = \dfrac{5}{4}:\dfrac{3}{4} + \left( {\dfrac{1}{4} - \dfrac{5}{6}} \right):\dfrac{{14}}{3}\)
\( = \dfrac{5}{4}.\dfrac{4}{3} + \left( {\dfrac{3}{{12}} - \dfrac{{10}}{{12}}} \right).\dfrac{3}{{14}}\)
\( = \dfrac{5}{3} + \dfrac{{ - 7}}{{12}}.\dfrac{3}{{14}}\)
\( = \dfrac{5}{3} + \dfrac{{ - 1}}{8} = \dfrac{{40}}{{24}} + \dfrac{{ - 3}}{{24}}= \dfrac{{37}}{{24}}\)
Bài 2
Phương pháp:
Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Cách giải:
a) \(\dfrac{{29}}{4}x - \dfrac{7}{6} = \dfrac{5}{4}\)
\(\dfrac{{29}}{4}x = \dfrac{5}{4} + \dfrac{7}{6}\)
\(\dfrac{{29}}{4}x = \dfrac{{29}}{{12}}\)
\(x = \dfrac{{29}}{{12}}:\dfrac{{29}}{4}\)
\(x = \dfrac{1}{3}\)
Vậy \(x = \dfrac{1}{3}\).
b) \(2\dfrac{3}{5}:\left( {6x - \dfrac{1}{2}} \right) = \dfrac{{13}}{{10}}\)
\(\dfrac{{13}}{5}:\left( {6x - \dfrac{1}{2}} \right) = \dfrac{{13}}{{10}}\)
\(6x - \dfrac{1}{2} = \dfrac{{13}}{5}:\dfrac{{13}}{{10}}\)
\(6x - \dfrac{1}{2} = 2\)
\(6x = 2 + \dfrac{1}{2}\)
\(6x = \dfrac{5}{2}\)
\(x = \dfrac{5}{2}:6\)
\(x = \dfrac{5}{{12}}\)
Vậy \(x = \dfrac{5}{{12}}\).
c) \(\dfrac{1}{3}.\left( {3x - 2} \right) + 25\% = - \dfrac{9}{6}\)
\(\dfrac{1}{3}\left( {3x - 2} \right) + \dfrac{1}{4} = - \dfrac{3}{2}\)
\(\dfrac{1}{3}\left( {3x - 2} \right) = - \dfrac{3}{2} - \dfrac{1}{4}\)
\(\dfrac{1}{3}\left( {3x - 2} \right) = \dfrac{{ - 7}}{4}\)
\(3x - 2 = \dfrac{{ - 7}}{4}:\dfrac{1}{3}\)
\(3x - 2 = \dfrac{{ - 21}}{4}\)
\(3x = \dfrac{{ - 21}}{4} + 2\)
\(3x = \dfrac{{ - 13}}{4}\)
\(x = \dfrac{{ - 13}}{4}:3\)
\(x = \dfrac{{ - 13}}{{12}}\)
Vậy \(x = \dfrac{{ - 13}}{{12}}\).
Bài 3
Phương pháp:
a) Quy tắc tìm giá trị phân số của một số cho trước: Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\left( {m,n \in \mathbb{N},n \ne 0} \right).\)
b) Quy tắc tìm một số khi biết giá trị phân số của nó: Muốn tìm một số biết \(\dfrac{m}{n}\) của nó bằng \(a\), ta tính \(a:\dfrac{m}{n}\left( {m,n \in {\mathbb{N}^*}} \right)\). Cách giải:
a) Đổi \(80\% {\rm{\;}} = \dfrac{4}{5}\).
Phân số chỉ số học sinh đạt giải ba so với số học sinh đạt giải nhất là: \(1 - \dfrac{4}{5} = \dfrac{1}{5}\) (số học sinh đạt giải nhất)
Số học sinh đạt giải nhất là: \(5:\dfrac{1}{5} = 25\) (học sinh)
Tổng số học sinh của đoàn đó là: \(25:\dfrac{1}{2} = 50\) (học sinh)
b) Theo câu ta có số học sinh đạt giải nhất là 25 học sinh.
Số học sinh đạt giải nhì là: \(25.80\% {\rm{\;}} = 20\) (học sinh)
Tỉ số phần trăm số học sinh đạt giải nhất so với tổng số học sinh đi thi là: \(25:50.100\% {\rm{\;}} = 50\% \)
Tỉ số phần trăm số học sinh đạt giải nhì so với tổng số học sinh đi thi là: \(20:50.100\% {\rm{\;}} = 40\% \)
Tỉ số phần trăm số học sinh đạt giải ba so với tổng số học sinh đi thi là: \(5:50.100\% {\rm{\;}} = 10\% \)
Bài 4
Phương pháp:
Dựa vào dấu hiệu nhận biết một điểm nằm giữa hai điểm và tính chất trung điểm của đoạn thẳng.
Cách giải:

a) Trên tia Ax ta có \(AM < AB\left( {4cm < 8cm} \right)\) suy ra điểm \(M\) nằm giữa hai điểm \(A\) và \(B\).
b) Theo câu a, điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) nên ta có: \(AM + MB = AB\)\( \Rightarrow MB = AB - AM = 8 - 4 = 4cm\)
Vậy \(AM = MB = 4cm\).
c) Theo câu a và b ta có: \(M\) nằm giữa hai điểm \(A\) và \(B\) và \(MA = MB\).
Vậy \(M\) là trung điểm của đoạn thẳng AB.
b) Trên tia Ax ta có \(AB < AN\left( {8cm < 12cm} \right)\) suy ra điểm B nằm giữa hai điểm A và N
\(\begin{array}{*{20}{l}}{ \Rightarrow AB + BN = AN}\\{ \Rightarrow BN = AN - AB = 12 - 8 = 4cm}\end{array}\)
Vậy \(MB = \;BN = 4cm\).
Bài 5
Phương pháp:
Phân tích \(A = a + \dfrac{b}{{3 - n}}\), với \(a,\,\,b \in \mathbb{Z}\).
Để \(A \in \mathbb{Z}\) thì \(3 - n \in U\left( b \right)\).
Cách giải:
\(\begin{array}{l}A = \dfrac{{2n - 1}}{{3 - n}} = \dfrac{{2n - 6 + 5}}{{ - n + 3}}\\\,\,\,\,\, = \dfrac{{2n - 6}}{{ - n + 3}} + \dfrac{5}{{ - n + 3}}\\\,\,\,\,\, = \dfrac{{ - 2\left( { - n + 3} \right)}}{{ - n + 3}} + \dfrac{5}{{ - n + 3}}\\\,\,\,\,\, = - 2 + \dfrac{5}{{ - n + 3}}\end{array}\)
Để A nhận giá trị nguyên thì \( - 2 + \dfrac{5}{{ - n + 3}} \in \mathbb{Z} \Rightarrow \dfrac{5}{{ - n + 3}} \in \mathbb{Z}\)\( \Rightarrow - n + 3 \in \left\{ { \pm 1; \pm 5} \right\}\)
Ta có bảng giá trị sau:

Vậy \(n \in \left\{ {2;4; - 2;8} \right\}\).
Đề thi học kì 2 Toán 6 - Đề số 8 tại giaitoan.edu.vn được xây dựng với mục tiêu đánh giá toàn diện kiến thức và kỹ năng của học sinh sau một học kỳ học tập. Đề thi bao gồm các chủ đề chính như số tự nhiên, số nguyên, phân số, phép tính với phân số, hình học cơ bản và giải toán có lời văn.
Đề thi được chia thành các phần nhỏ, mỗi phần tập trung vào một chủ đề cụ thể. Dưới đây là chi tiết nội dung đề thi:
Việc luyện tập với Đề thi học kì 2 Toán 6 - Đề số 8 tại giaitoan.edu.vn mang lại nhiều lợi ích cho học sinh:
Sau khi hoàn thành đề thi, học sinh có thể tham khảo đáp án chi tiết và lời giải của từng bài tập tại giaitoan.edu.vn. Đáp án được trình bày rõ ràng, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và khắc phục những sai lầm.
Để đạt kết quả tốt nhất khi làm đề thi, học sinh nên:
Ngoài Đề thi học kì 2 Toán 6 - Đề số 8, giaitoan.edu.vn còn cung cấp nhiều đề thi khác với các mức độ khó khác nhau. Học sinh có thể lựa chọn các đề thi phù hợp với năng lực của bản thân để luyện tập và nâng cao kiến thức.
Đề thi học kì 2 Toán 6 - Đề số 8 tại giaitoan.edu.vn là một công cụ hữu ích giúp học sinh ôn tập và chuẩn bị tốt nhất cho kỳ thi. Chúc các em học sinh đạt kết quả cao trong kỳ thi sắp tới!