Chào mừng các em học sinh đến với đề thi học kì 2 Toán 6 - Đề số 3 chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 2 môn Toán 6.
Với cấu trúc đề thi bám sát chương trình học và đáp án chi tiết, các em có thể tự tin làm bài và cải thiện kết quả học tập.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho đoạn thẳng AB = 6 cm. Điểm K nằm giữa AB, biết KA = 4 cm thì đoạn thẳng KB bằng:
A. 10 cm
B. 6 cm
C. 4 cm
D. 2 cm
Câu 2:Bạn Nam có một cái hộp đựng 1 chiếc bút xanh, 2 chiếc bút đỏ và 1 chiếc bút đen. Nam lấy ngẫu nhiên cùng lúc 3 chiếc bút trong hộp. Kết quả nào sau đây chắc chắn sẽ xảy ra?
A. Luôn lấy được một chiếc bút đỏ.
B. Luôn lấy được một chiếc bút xanh.
C. Luôn lấy được một chiếc bút đen.
D. Luôn lấy được 3 chiếc, ba màu khác nhau.
Câu 3: Thực hiện phép tính rồi làm tròn kết quả đến hàng phần trăm: \(96,3\,.\,3,007\)
A. \(289,5\)
B. \(289,57\)
C. \(289,58\)
D. \(289,6\)
Câu 4:Cho \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{1}{4}\) thì giá trị của \(x\) và \(y\) là:
A. \(x = 4;y = 9\)
B. \(x = - 4;y = - 9\)
C. \(x = 12;y = 3\)
D. \(x = - 12;y = - 3\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (Tính hợp lý nếu có thể)
a) \(2\dfrac{1}{9} - \dfrac{1}{3}:\dfrac{3}{7}\)
b) \(\dfrac{7}{{19}}.\dfrac{8}{{11}} + \dfrac{3}{{11}}.\dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}}\)
c) \(20\dfrac{8}{{23}} - \left( {5\dfrac{7}{{32}} + 14\dfrac{8}{{23}}} \right)\)
d) \(75\% {\rm{\;}} - 1\dfrac{1}{2} + 0,5:\dfrac{5}{{12}} - {\left( { - \dfrac{1}{2}} \right)^2}\)
Bài 2:(1,5 điểm)Tìm x biết:
\(a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\,\)
\(b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\)
\(c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\)
Bài 3 (1,5 điểm) Một bác nông dân vừa thu hoạch 30,8 kg cà chua và 12 kg đậu đũa.
a) Bác đem số cà chua đó đi bán hết, giá mỗi kg cà chua là 15 000 đồng. Hỏi bác nông dân nhận được bao nhiêu tiền?
b) Số đậu đũa bác vừa thu hoạch chỉ bằng \(\dfrac{2}{5}\) số đậu đũa có trong vườn. Nếu bác thu hoạch hết tất cả thì thu được bao nhiêu kg đậu đũa?
Bài 4: (2,5 điểm) Trên tia \(Ox\) lấy hai điểm \(A, B\) sao cho \(OA = 5cm, OB = 8cm\).
a) Trong ba điểm \(O, A, B\) điểm nào nằm giữa hai điểm còn lại?
b) Tính độ dài đoạn thẳng \(AB\).
c) Điểm \(A\) có phải là trung điểm của đoạn thẳng \(OB\) không? Vì sao?
d) Gọi \(M\) là trung điểm của \(OA\), \(N\) là trung điểm của \(AB\). Tính độ dài đoạn thẳng \(MN\)?
Bài 5:(0,5 điểm)Tính nhanh : \(S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}} + ... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}\).
Tải về
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho đoạn thẳng AB = 6 cm. Điểm K nằm giữa AB, biết KA = 4 cm thì đoạn thẳng KB bằng:
A. 10 cm
B. 6 cm
C. 4 cm
D. 2 cm
Câu 2:Bạn Nam có một cái hộp đựng 1 chiếc bút xanh, 2 chiếc bút đỏ và 1 chiếc bút đen. Nam lấy ngẫu nhiên cùng lúc 3 chiếc bút trong hộp. Kết quả nào sau đây chắc chắn sẽ xảy ra?
A. Luôn lấy được một chiếc bút đỏ.
B. Luôn lấy được một chiếc bút xanh.
C. Luôn lấy được một chiếc bút đen.
D. Luôn lấy được 3 chiếc, ba màu khác nhau.
Câu 3: Thực hiện phép tính rồi làm tròn kết quả đến hàng phần trăm: \(96,3\,.\,3,007\)
A. \(289,5\)
B. \(289,57\)
C. \(289,58\)
D. \(289,6\)
Câu 4:Cho \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{1}{4}\) thì giá trị của \(x\) và \(y\) là:
A. \(x = 4;y = 9\)
B. \(x = - 4;y = - 9\)
C. \(x = 12;y = 3\)
D. \(x = - 12;y = - 3\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (Tính hợp lý nếu có thể)
a) \(2\dfrac{1}{9} - \dfrac{1}{3}:\dfrac{3}{7}\)
b) \(\dfrac{7}{{19}}.\dfrac{8}{{11}} + \dfrac{3}{{11}}.\dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}}\)
c) \(20\dfrac{8}{{23}} - \left( {5\dfrac{7}{{32}} + 14\dfrac{8}{{23}}} \right)\)
d) \(75\% {\rm{\;}} - 1\dfrac{1}{2} + 0,5:\dfrac{5}{{12}} - {\left( { - \dfrac{1}{2}} \right)^2}\)
Bài 2:(1,5 điểm)Tìm x biết:
\(a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\,\)
\(b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\)
\(c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\)
Bài 3 (1,5 điểm) Một bác nông dân vừa thu hoạch 30,8 kg cà chua và 12 kg đậu đũa.
a) Bác đem số cà chua đó đi bán hết, giá mỗi kg cà chua là 15 000 đồng. Hỏi bác nông dân nhận được bao nhiêu tiền?
b) Số đậu đũa bác vừa thu hoạch chỉ bằng \(\dfrac{2}{5}\) số đậu đũa có trong vườn. Nếu bác thu hoạch hết tất cả thì thu được bao nhiêu kg đậu đũa?
Bài 4: (2,5 điểm) Trên tia \(Ox\) lấy hai điểm \(A, B\) sao cho \(OA = 5cm, OB = 8cm\).
a) Trong ba điểm \(O, A, B\) điểm nào nằm giữa hai điểm còn lại?
b) Tính độ dài đoạn thẳng \(AB\).
c) Điểm \(A\) có phải là trung điểm của đoạn thẳng \(OB\) không? Vì sao?
d) Gọi \(M\) là trung điểm của \(OA\), \(N\) là trung điểm của \(AB\). Tính độ dài đoạn thẳng \(MN\)?
Bài 5:(0,5 điểm)Tính nhanh : \(S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}} + ... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}\).
Phần I: Trắc nghiệm
1. D | 2. A | 3. B | 4. C |
Câu 1
Phương pháp:
Dựa vào tính chất điểm nằm giữa hai điểm: Khi M nằm giữa A và B thì \(AM + MB = AB\)
Cách giải:
Vì K nằm giữa A và B nên ta có: \(AK + KB = AB\)
Hay \(4 + KB = 6\)
Suy ra: \(KB = 6 - 4 = 2\left( {cm} \right)\)
Chọn D.
Câu 2
Phương pháp:
Liệt kê các trường hợp có thể xảy ra
Cách giải:
Lấy ngẫu nhiên \(3\) chiếc bút có thể đưa ra các kết quả sau:
+ Trường hợp 1: \(1\) xanh, \(1\) đỏ, \(1\) đen.
+ Trường hợp 2: \(1\) xanh, \(2\) đỏ.
+ Trường hợp 3: \(2\) đỏ, \(1\) đen.
Ta thấy trong cả 3 trường hợp trên ta luôn lấy được ít nhất \(1\) chiếc bút màu đỏ.
Chọn A.
Câu 3
Phương pháp:
Thực hiện phép tính nhân hai số thập phân.
Cách giải:
Ta có: \(96,3\,.\,3,007 = 289,5741 \approx 289,57\)
Chọn B.
Câu 4
Phương pháp:
Quy đồng mẫu số để tìm y, quy đồng tử số để tìm x.
Cách giải:
Ta có: \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{3}{{12}}\)
Vậy: \(x = 12;y = 3\)
Chọn C.
Phần II: Tự luận
Bài 1
Phương pháp
Áp dụng các quy tắc:
- Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc: Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ.
- Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc: \(() \to [] \to \{ \} \)
Cách giải:
a) \(2\dfrac{1}{9} - \dfrac{1}{3}:\dfrac{3}{7}\)
\(\begin{array}{l} = \dfrac{{19}}{9} - \dfrac{1}{3}.\dfrac{7}{3}\\ = \dfrac{{19}}{9} - \dfrac{7}{9}\\ = \dfrac{{12}}{9} = \dfrac{4}{3}\end{array}\)
b) \(\dfrac{7}{{19}}.\dfrac{8}{{11}} + \dfrac{3}{{11}}.\dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}}\)
\(\begin{array}{l} = \dfrac{7}{{19}}.\left( {\dfrac{8}{{11}} + \dfrac{3}{{11}}} \right) + \dfrac{{ - 12}}{{19}}\\ = \dfrac{7}{{19}}.\dfrac{{11}}{{11}} + \dfrac{{ - 12}}{{19}}\\ = \dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}} = \dfrac{{ - 5}}{{19}}\end{array}\)
c) \(20\dfrac{8}{{23}} - \left( {5\dfrac{7}{{32}} + 14\dfrac{8}{{23}}} \right)\)
\(\begin{array}{l} = 20 + \dfrac{8}{{23}} - \left( {5 + \dfrac{7}{{32}} + 14 + \dfrac{8}{{23}}} \right)\\ = 20 + \dfrac{8}{{23}} - 5 - \dfrac{7}{{32}} - 14 - \dfrac{8}{{23}}\\ = \left( {20 - 5 - 14} \right) + \left( {\dfrac{8}{{23}} - \dfrac{8}{{23}}} \right) - \dfrac{7}{{32}}\\ = 1 + 0 - \dfrac{7}{{32}}\\ = 1 - \dfrac{7}{{32}}\\ = \dfrac{{32}}{{32}} - \dfrac{7}{{32}}\\ = \dfrac{{25}}{{32}}\end{array}\)
d) \(75\% - 1\dfrac{1}{2} + 0,5:\dfrac{5}{{12}} - {\left( { - \dfrac{1}{2}} \right)^2}\)
\(\begin{array}{l} = \dfrac{3}{4} - \dfrac{3}{2} + \dfrac{1}{2}.\dfrac{{12}}{5} - \dfrac{1}{4}\\ = \dfrac{3}{4} - \dfrac{3}{2} + \dfrac{6}{5} - \dfrac{1}{4}\\ = \dfrac{3}{4} - \dfrac{1}{4} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{2}{4} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{1}{2} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{{ - 2}}{2} + \dfrac{6}{5}\\ = - 1 + \dfrac{6}{5}\\ = \dfrac{{ - 5}}{5} + \dfrac{6}{5} = \dfrac{1}{5}\end{array}\)
Bài 2:
Phương pháp: Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Cách giải:
\(\begin{array}{l}a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\\\,\,\,\,\,\,x - \dfrac{1}{3} = \dfrac{{ - 5}}{{12}}\,\,\,\\\,\,\,\,\,\,x = \dfrac{{ - 5}}{{12}}\, + \dfrac{1}{3}\,\\\,\,\,\,\,\,x = \dfrac{{ - 1}}{{12}}\,\end{array}\)
Vậy \(x = \dfrac{{ - 1}}{{12}}\)
\(\begin{array}{l}\,b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\,\\\,\,\,\,\,\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = \dfrac{1}{5}\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{1}{5} - \dfrac{3}{4}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{{ - 11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\,\dfrac{{ - 11}}{{20}}:\dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\dfrac{{ - 11}}{5}\end{array}\)
Vậy \(x = \dfrac{{ - 11}}{5}\)
\(\begin{array}{l}c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\\\,\dfrac{1}{{12}}.{x^2} = \dfrac{4}{3}\\{x^2} = \dfrac{4}{3}:\dfrac{1}{{12}}\\{x^2} = 16\\ \Rightarrow \,\left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\end{array}\)
Vậy \(x \in \left\{ {4; - 4} \right\}\)
Bài 3
Phương pháp:
a) Lấy giá tiền 1 kg cà chua nhân với khối lượng cà chua.
b) Lấy khối lượng đậu đũa vừa thu hoạch chia cho \(\dfrac{2}{5}\).
Cách giải:
a) Số tiền bác nông dân nhận được là: \(15000.30,8 = 462000\)(đồng)
b) Nếu thu hoạch hết thì thu được số ki-lô-gam đậu đũa là: \(12:\dfrac{2}{5} = 30\)(kg)
Bài 4
Phương pháp
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.
Cách giải:
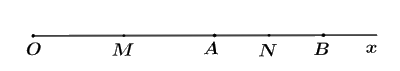
a) Ta có: \(A\) và \(B\) cùng thuộc tia \(Ox\) và \(OA < OB\left( {5cm < 8cm} \right)\) nên \(A\) nằm giữa \(O\) và \(B\).
b) Vì \(A\) nằm giữa \(O\) và \(B\) nên ta có:
\(OB = OA + AB\)
\(AB = OB - OA\)
\(AB = 8cm - 5cm\)
\(AB = 3cm\)
c) Vì \(AB = 3cm\) và \(OA = 5cm\) suy ra \(AB \ne OA\) nên \(A\) không phải là trung điểm của \(OB\).
Vì \(M\) là trung điểm của \(AO\) nên \(MA = \dfrac{{OA}}{2} = \dfrac{5}{2} = 2,5\left( {cm} \right)\)
Vì \(N\) là trung điểm của \(AB\) nên \(NA = \dfrac{{AB}}{2} = \dfrac{3}{2} = 1,5\left( {cm} \right)\)
Vì \(A\) nằm giữa \(O\) và \(B\) nên \(AO\) và \(AB\) là hai tia đối nhau.
Mặt khác, \(M\) là trung điểm của \(OA\) và \(N\) là trung điểm của \(AB\) nên \(A\) nằm giữa \(M\) và \(N\).
Do đó, ta có: \(MN = MA + AN = 2,5cm + 1,5cm = 4cm\)
Vậy \(MN = 4cm\).
Bài 5
Phương pháp
Đưa tổng đã cho về dạng: \(S = 1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}.\)
Tính \(\dfrac{1}{2}S\) sau đó suy ra giá trị của biểu thức \(S.\)
Cách giải:
\(\begin{array}{*{20}{l}}{S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}} + ... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}}\\{ = 1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}}\\{ \Rightarrow \dfrac{1}{2}.S = \dfrac{1}{2}\left( {1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}} \right)}\\{ = \dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{{12}} + \dfrac{1}{{20}} + ... + \dfrac{1}{{72}}}\\{ = \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{8.9}}}\\{ = \left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + \dfrac{1}{4} - \dfrac{1}{5} + ... + \dfrac{1}{8} - \dfrac{1}{9}} \right)}\\{ = 1 - \dfrac{1}{9} = \dfrac{8}{9}}\\{ \Rightarrow \dfrac{1}{2}S = \dfrac{8}{9}}\\{ \Rightarrow S = \dfrac{8}{9}:\dfrac{1}{2} = \dfrac{{16}}{9}.}\end{array}\)
Phần I: Trắc nghiệm
1. D | 2. A | 3. B | 4. C |
Câu 1
Phương pháp:
Dựa vào tính chất điểm nằm giữa hai điểm: Khi M nằm giữa A và B thì \(AM + MB = AB\)
Cách giải:
Vì K nằm giữa A và B nên ta có: \(AK + KB = AB\)
Hay \(4 + KB = 6\)
Suy ra: \(KB = 6 - 4 = 2\left( {cm} \right)\)
Chọn D.
Câu 2
Phương pháp:
Liệt kê các trường hợp có thể xảy ra
Cách giải:
Lấy ngẫu nhiên \(3\) chiếc bút có thể đưa ra các kết quả sau:
+ Trường hợp 1: \(1\) xanh, \(1\) đỏ, \(1\) đen.
+ Trường hợp 2: \(1\) xanh, \(2\) đỏ.
+ Trường hợp 3: \(2\) đỏ, \(1\) đen.
Ta thấy trong cả 3 trường hợp trên ta luôn lấy được ít nhất \(1\) chiếc bút màu đỏ.
Chọn A.
Câu 3
Phương pháp:
Thực hiện phép tính nhân hai số thập phân.
Cách giải:
Ta có: \(96,3\,.\,3,007 = 289,5741 \approx 289,57\)
Chọn B.
Câu 4
Phương pháp:
Quy đồng mẫu số để tìm y, quy đồng tử số để tìm x.
Cách giải:
Ta có: \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{3}{{12}}\)
Vậy: \(x = 12;y = 3\)
Chọn C.
Phần II: Tự luận
Bài 1
Phương pháp
Áp dụng các quy tắc:
- Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc: Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ.
- Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc: \(() \to [] \to \{ \} \)
Cách giải:
a) \(2\dfrac{1}{9} - \dfrac{1}{3}:\dfrac{3}{7}\)
\(\begin{array}{l} = \dfrac{{19}}{9} - \dfrac{1}{3}.\dfrac{7}{3}\\ = \dfrac{{19}}{9} - \dfrac{7}{9}\\ = \dfrac{{12}}{9} = \dfrac{4}{3}\end{array}\)
b) \(\dfrac{7}{{19}}.\dfrac{8}{{11}} + \dfrac{3}{{11}}.\dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}}\)
\(\begin{array}{l} = \dfrac{7}{{19}}.\left( {\dfrac{8}{{11}} + \dfrac{3}{{11}}} \right) + \dfrac{{ - 12}}{{19}}\\ = \dfrac{7}{{19}}.\dfrac{{11}}{{11}} + \dfrac{{ - 12}}{{19}}\\ = \dfrac{7}{{19}} + \dfrac{{ - 12}}{{19}} = \dfrac{{ - 5}}{{19}}\end{array}\)
c) \(20\dfrac{8}{{23}} - \left( {5\dfrac{7}{{32}} + 14\dfrac{8}{{23}}} \right)\)
\(\begin{array}{l} = 20 + \dfrac{8}{{23}} - \left( {5 + \dfrac{7}{{32}} + 14 + \dfrac{8}{{23}}} \right)\\ = 20 + \dfrac{8}{{23}} - 5 - \dfrac{7}{{32}} - 14 - \dfrac{8}{{23}}\\ = \left( {20 - 5 - 14} \right) + \left( {\dfrac{8}{{23}} - \dfrac{8}{{23}}} \right) - \dfrac{7}{{32}}\\ = 1 + 0 - \dfrac{7}{{32}}\\ = 1 - \dfrac{7}{{32}}\\ = \dfrac{{32}}{{32}} - \dfrac{7}{{32}}\\ = \dfrac{{25}}{{32}}\end{array}\)
d) \(75\% - 1\dfrac{1}{2} + 0,5:\dfrac{5}{{12}} - {\left( { - \dfrac{1}{2}} \right)^2}\)
\(\begin{array}{l} = \dfrac{3}{4} - \dfrac{3}{2} + \dfrac{1}{2}.\dfrac{{12}}{5} - \dfrac{1}{4}\\ = \dfrac{3}{4} - \dfrac{3}{2} + \dfrac{6}{5} - \dfrac{1}{4}\\ = \dfrac{3}{4} - \dfrac{1}{4} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{2}{4} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{1}{2} - \dfrac{3}{2} + \dfrac{6}{5}\\ = \dfrac{{ - 2}}{2} + \dfrac{6}{5}\\ = - 1 + \dfrac{6}{5}\\ = \dfrac{{ - 5}}{5} + \dfrac{6}{5} = \dfrac{1}{5}\end{array}\)
Bài 2:
Phương pháp: Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Cách giải:
\(\begin{array}{l}a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\\\,\,\,\,\,\,x - \dfrac{1}{3} = \dfrac{{ - 5}}{{12}}\,\,\,\\\,\,\,\,\,\,x = \dfrac{{ - 5}}{{12}}\, + \dfrac{1}{3}\,\\\,\,\,\,\,\,x = \dfrac{{ - 1}}{{12}}\,\end{array}\)
Vậy \(x = \dfrac{{ - 1}}{{12}}\)
\(\begin{array}{l}\,b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\,\\\,\,\,\,\,\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = \dfrac{1}{5}\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{1}{5} - \dfrac{3}{4}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{{ - 11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\,\dfrac{{ - 11}}{{20}}:\dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\dfrac{{ - 11}}{5}\end{array}\)
Vậy \(x = \dfrac{{ - 11}}{5}\)
\(\begin{array}{l}c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\\\,\dfrac{1}{{12}}.{x^2} = \dfrac{4}{3}\\{x^2} = \dfrac{4}{3}:\dfrac{1}{{12}}\\{x^2} = 16\\ \Rightarrow \,\left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\end{array}\)
Vậy \(x \in \left\{ {4; - 4} \right\}\)
Bài 3
Phương pháp:
a) Lấy giá tiền 1 kg cà chua nhân với khối lượng cà chua.
b) Lấy khối lượng đậu đũa vừa thu hoạch chia cho \(\dfrac{2}{5}\).
Cách giải:
a) Số tiền bác nông dân nhận được là: \(15000.30,8 = 462000\)(đồng)
b) Nếu thu hoạch hết thì thu được số ki-lô-gam đậu đũa là: \(12:\dfrac{2}{5} = 30\)(kg)
Bài 4
Phương pháp
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.
Cách giải:
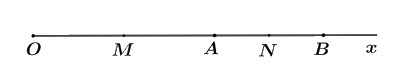
a) Ta có: \(A\) và \(B\) cùng thuộc tia \(Ox\) và \(OA < OB\left( {5cm < 8cm} \right)\) nên \(A\) nằm giữa \(O\) và \(B\).
b) Vì \(A\) nằm giữa \(O\) và \(B\) nên ta có:
\(OB = OA + AB\)
\(AB = OB - OA\)
\(AB = 8cm - 5cm\)
\(AB = 3cm\)
c) Vì \(AB = 3cm\) và \(OA = 5cm\) suy ra \(AB \ne OA\) nên \(A\) không phải là trung điểm của \(OB\).
Vì \(M\) là trung điểm của \(AO\) nên \(MA = \dfrac{{OA}}{2} = \dfrac{5}{2} = 2,5\left( {cm} \right)\)
Vì \(N\) là trung điểm của \(AB\) nên \(NA = \dfrac{{AB}}{2} = \dfrac{3}{2} = 1,5\left( {cm} \right)\)
Vì \(A\) nằm giữa \(O\) và \(B\) nên \(AO\) và \(AB\) là hai tia đối nhau.
Mặt khác, \(M\) là trung điểm của \(OA\) và \(N\) là trung điểm của \(AB\) nên \(A\) nằm giữa \(M\) và \(N\).
Do đó, ta có: \(MN = MA + AN = 2,5cm + 1,5cm = 4cm\)
Vậy \(MN = 4cm\).
Bài 5
Phương pháp
Đưa tổng đã cho về dạng: \(S = 1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}.\)
Tính \(\dfrac{1}{2}S\) sau đó suy ra giá trị của biểu thức \(S.\)
Cách giải:
\(\begin{array}{*{20}{l}}{S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}} + ... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}}\\{ = 1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}}\\{ \Rightarrow \dfrac{1}{2}.S = \dfrac{1}{2}\left( {1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}} \right)}\\{ = \dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{{12}} + \dfrac{1}{{20}} + ... + \dfrac{1}{{72}}}\\{ = \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{8.9}}}\\{ = \left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + \dfrac{1}{4} - \dfrac{1}{5} + ... + \dfrac{1}{8} - \dfrac{1}{9}} \right)}\\{ = 1 - \dfrac{1}{9} = \dfrac{8}{9}}\\{ \Rightarrow \dfrac{1}{2}S = \dfrac{8}{9}}\\{ \Rightarrow S = \dfrac{8}{9}:\dfrac{1}{2} = \dfrac{{16}}{9}.}\end{array}\)
Đề thi học kì 2 Toán 6 - Đề số 3 chương trình Kết nối tri thức là một công cụ quan trọng giúp học sinh lớp 6 ôn tập và củng cố kiến thức đã học trong suốt học kì. Đề thi này bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp học sinh rèn luyện kỹ năng giải toán và làm quen với cấu trúc đề thi thực tế.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để đạt kết quả tốt trong kỳ thi học kì, học sinh cần:
Bài 1: Tính giá trị của biểu thức: 12 + 3 x 4 - 5
Lời giải:
12 + 3 x 4 - 5 = 12 + 12 - 5 = 24 - 5 = 19
Bài 2: Tìm x biết: x + 5 = 10
Lời giải:
x + 5 = 10
x = 10 - 5
x = 5
Việc ôn tập kỹ lưỡng trước kỳ thi là rất quan trọng. Học sinh nên dành thời gian để xem lại các bài giảng, làm lại các bài tập đã học và giải các đề thi thử. Điều này sẽ giúp các em tự tin hơn và đạt kết quả tốt nhất trong kỳ thi.
Giaitoan.edu.vn cung cấp một nền tảng học toán online hiệu quả với nhiều tài liệu học tập, bài giảng, bài tập và đề thi thử. Các em có thể sử dụng giaitoan.edu.vn để ôn tập kiến thức, rèn luyện kỹ năng và chuẩn bị tốt nhất cho kỳ thi học kì.
Hãy luôn giữ tinh thần học tập tích cực, chủ động tìm tòi và giải quyết các vấn đề khó khăn. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học tốt và đạt kết quả cao trong kỳ thi học kì!
| Chủ đề | Nội dung chính |
|---|---|
| Số tự nhiên | Các phép tính cộng, trừ, nhân, chia; tính chất của các phép tính. |
| Tập hợp | Các khái niệm về tập hợp, phần tử của tập hợp, các phép toán trên tập hợp. |
| Phân số | Các khái niệm về phân số, so sánh phân số, các phép toán trên phân số. |
| Số thập phân | Các khái niệm về số thập phân, so sánh số thập phân, các phép toán trên số thập phân. |