Đề thi giữa kì 1 Toán 6 - Đề số 18 là một công cụ ôn tập vô cùng hữu ích dành cho các em học sinh. Đề thi được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp đề thi kèm theo đáp án chi tiết, giúp các em tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Theo Âm Lịch, năm 2024 là năm Giáp Thìn, tức năm con Rồng – xếp thứ năm trong 12 con giáp. Năm Giáp Thìn sẽ bắt đầu từ ngày 10/02/2024 và kết thúc năm vào ngày 28/01/2025 theo lịch dương. Gọi A là tập hợp các chữ số xuất hiện ở hình bên. Khi đó

\(A = \left\{ {4;2;0;2} \right\}\).
\(A = \left\{ {2;0;2;4} \right\}\).
\(A = \left\{ {0;2;4} \right\}\).
\(A = \left\{ {0;2} \right\}\).
Cho tập hợp \(A = \left\{ {1;\,\,2;\,\,a;\,\,b} \right\}\). Khẳng định nào dưới đây sai?
\(1 \in A\).
\(a \in A\).
\(5 \notin A\).
\(b \notin A\).
Cho số tự nhiên x, biết \(x + 20 = 55\). Khi đó
\(x = 20\).
\(x = 25\).
\(x = 30\).
\(x = 35\).
Phép tính \({3^{40}}{.3^{200}}:{3^{50}}\) có kết quả là:
\({3^{54}}\).
\({3^{100}}\).
\({3^{50}}\).
\({3^{190}}\).
Kết quả của phép tính \(37.64 + 37.36\) là
3700.
3600.
370.
6400.
Trong các số tự nhiên sau số nào là số nguyên tố?
1.
5.
9.
12.
Khẳng định nào sau đây là đúng?
Số 2 là số nguyên tố chẵn duy nhất.
Số 0 là số nguyên tố.
Các số nguyên tố nhỏ hơn 10 là 3; 5; 7; 9 .
Các số nguyên tố đều là số lẻ.
Tổng chia hết cho 3 là:
145 + 207.
875 + 27.
379 + 978.
207 + 708.
Trong các hình sau đây, hình nào là tam giác đều?

HÌNH 1.
HÌNH 2.
HÌNH 3.
HÌNH 4.
Cho hình chữ nhật ABCD như hình vẽ. Khẳng định nào sau đây là đúng?
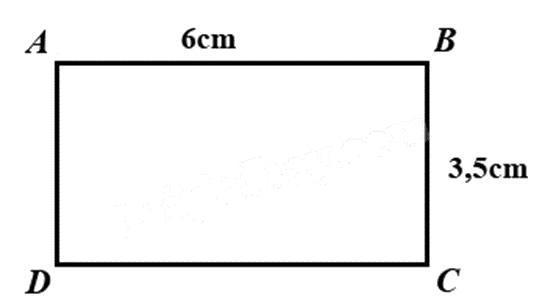
Cạnh AD và cạnh BA song song với nhau.
CD = 6cm.
BD = 3,5cm.
Cạnh AC và cạnh BD song song với nhau.
Cho hình vuông ABCD với đường chéo AC = 11 cm. Tính độ dài đoạn thẳng BD.
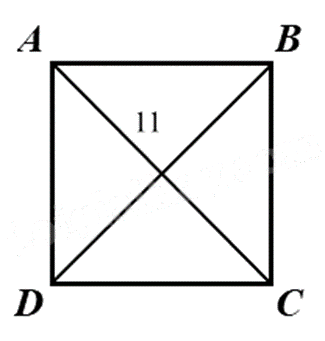
BD = 10cm.
BD = 9cm.
BD = 11cm.
BD = 12cm.
Hình bình hành không có tính chất nào sau đây?
Hai cạnh đối song song với nhau.
Hai cạnh đối bằng nhau.
Bốn cạnh bằng nhau.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Hội nghị lần thứ 10 Ban Chấp hành Trung ương Đảng khóa XIII họp từ ngày 18/9 đến ngày 20/9/2024 tại Thủ đô Hà Nội để xem xét thảo luận, cho ý kiến các tờ trình, đề án, báo cáo của Bộ Chính trị liên quan một số vấn đề lớn, cơ bản và quan trọng.

Em hãy cho biết:
- Số La Mã XIII đề cập phía trên có giá trị là bao nhiêu trong hệ thập phân?
- Số 3; 9 được viết ở dạng số La Mã như thế nào?
Thực hiện các phép tính sau:
a) \(52.26 + 52.74\)
b) \({3^2}.2 - {7^{10}}:{7^9} + {2024^0}\)
c) \(107 - \left\{ {38 + \left[ {{{7.3}^2} - 24:6 + {{\left( {9 - 7} \right)}^3}} \right]} \right\}:15\)
Tìm x, biết
a) \(12x - 33 = {3^2}{.3^3}\)
b) \(2\left( {x - 51} \right) = {2.2^3} + 20\)
Mỗi người khi ăn sẽ hấp thụ ca - lo và khi hoạt động thì sẽ tiêu hao ca - lo. Bạn Minh thống kê số ca - lo hằng ngày của mình, em hãy giúp bạn Minh tính tổng số ca – lo còn lại sau khi ăn sáng và thực hiện các hoạt động như bảng bên.

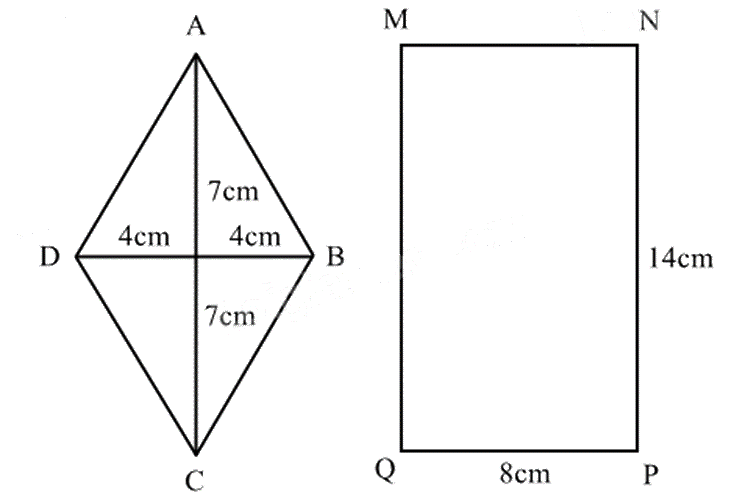
Cho hai hình vẽ bêna) Tính diện tích của hình thoi ABCD và diện tích của hình chữ nhật MNPQ.b) Diện tích của hình chữ nhật MNPQ gấp mấy lần diện tích của hình thoi ABCD.
Chứng minh rằng \(A = {20^{20}} + {20^{21}} + {20^{22}} + {20^{23}} + ..... + {20^{70}} + {20^{71}}\) chia hết cho 21.
Theo Âm Lịch, năm 2024 là năm Giáp Thìn, tức năm con Rồng – xếp thứ năm trong 12 con giáp. Năm Giáp Thìn sẽ bắt đầu từ ngày 10/02/2024 và kết thúc năm vào ngày 28/01/2025 theo lịch dương. Gọi A là tập hợp các chữ số xuất hiện ở hình bên. Khi đó

\(A = \left\{ {4;2;0;2} \right\}\).
\(A = \left\{ {2;0;2;4} \right\}\).
\(A = \left\{ {0;2;4} \right\}\).
\(A = \left\{ {0;2} \right\}\).
Đáp án : C
Dựa vào kiến thức về tập hợp.
Trong hình có các số 2; 0; 4 xuất hiện nên tập A là: \(A = \left\{ {0;2;4} \right\}\).
Đáp án C.
Cho tập hợp \(A = \left\{ {1;\,\,2;\,\,a;\,\,b} \right\}\). Khẳng định nào dưới đây sai?
\(1 \in A\).
\(a \in A\).
\(5 \notin A\).
\(b \notin A\).
Đáp án : D
Xác định phần tử thuộc và không thuộc tập hợp.
Tập hợp A có các phần tử 1; 2; a; b nên đáp án A, B đúng, D sai.
5 không thuộc tập A nên C. \(5 \notin A\) đúng.
Đáp án D.
Cho số tự nhiên x, biết \(x + 20 = 55\). Khi đó
\(x = 20\).
\(x = 25\).
\(x = 30\).
\(x = 35\).
Đáp án : D
Sử dụng quy tắc chuyển vế để tìm x.
Ta có:
\(\begin{array}{l}x + 20 = 55\\x = 55 - 20\\x = 35\end{array}\)
Đáp án D.
Phép tính \({3^{40}}{.3^{200}}:{3^{50}}\) có kết quả là:
\({3^{54}}\).
\({3^{100}}\).
\({3^{50}}\).
\({3^{190}}\).
Đáp án : D
Nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\).
Chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0;m \ge n \ge 0} \right)\).
Ta có:
\({3^{40}}{.3^{200}}:{3^{50}} = {3^{40 + 200 - 50}} = {3^{190}}\).
Đáp án D.
Kết quả của phép tính \(37.64 + 37.36\) là
3700.
3600.
370.
6400.
Đáp án : A
Sử dụng tính chất phân phối của phép nhân với phép cộng.
Ta có:
\(37.64 + 37.36 = 37\left( {64 + 36} \right) = 37.100 = 3700\).
Đáp án A.
Trong các số tự nhiên sau số nào là số nguyên tố?
1.
5.
9.
12.
Đáp án : B
Số nguyên tố là các số chỉ có 2 ước là 1 và chính nó.
Trong các số trên chỉ có 5 là số nguyên tố.
Đáp án B.
Khẳng định nào sau đây là đúng?
Số 2 là số nguyên tố chẵn duy nhất.
Số 0 là số nguyên tố.
Các số nguyên tố nhỏ hơn 10 là 3; 5; 7; 9 .
Các số nguyên tố đều là số lẻ.
Đáp án : A
Dựa vào kiến thức về số nguyên tố.
Chỉ có số 2 là số nguyên tố chẵn duy nhất nên A là khẳng định đúng.
Số 0 không phải số nguyên tố nên B sai.
Số 9 có 3 ước là 1; 3; 9, không phải số nguyên tố nên C sai.
Số 2 là số nguyên tố chẵn nên D sai.
Đáp án A.
Tổng chia hết cho 3 là:
145 + 207.
875 + 27.
379 + 978.
207 + 708.
Đáp án : D
Sử dụng dấu hiệu chia hết cho 3 tính chất chia hết của một tổng.
A. \(145\not{ \vdots }3\) và \(207 \vdots 3\) nên \(\left( {145 + 207} \right)\not{ \vdots }3\).
B. \(875\not{ \vdots }3\) và \(27 \vdots 3\) nên \(\left( {875 + 27} \right)\not{ \vdots }3\).
C. \(379\not{ \vdots }3\) và \(978 \vdots 3\) nên \(\left( {379 + 978} \right)\not{ \vdots }3\).
D. \(207 \vdots 3\) và \(708 \vdots 3\) nên \(\left( {207 + 708} \right) \vdots 3\).
Đáp án D.
Trong các hình sau đây, hình nào là tam giác đều?

HÌNH 1.
HÌNH 2.
HÌNH 3.
HÌNH 4.
Đáp án : A
Tam giác đều có 3 cạnh bằng nhau.
Ta thấy HÌNH 1 là tam giác có 3 cạnh bằng nhau nên là tam giác đều.
Đáp án A.
Cho hình chữ nhật ABCD như hình vẽ. Khẳng định nào sau đây là đúng?
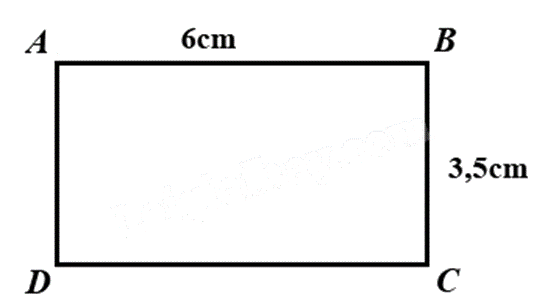
Cạnh AD và cạnh BA song song với nhau.
CD = 6cm.
BD = 3,5cm.
Cạnh AC và cạnh BD song song với nhau.
Đáp án : B
Hình chữ nhật có các cạnh đối song song và bằng nhau.
Vì ABCD là hình chữ nhật nên \(AB = CD = 6cm\), \(AD = BC = 3,5cm\), cạnh AB và CD song song với nhau, cạnh AD và BC song song với nhau nên chỉ có khẳng định B đúng.
Đáp án B.
Cho hình vuông ABCD với đường chéo AC = 11 cm. Tính độ dài đoạn thẳng BD.
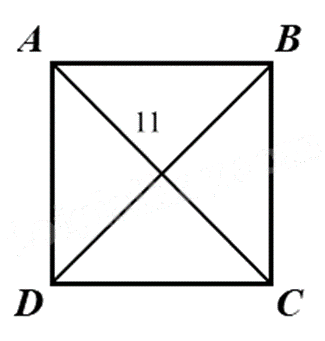
BD = 10cm.
BD = 9cm.
BD = 11cm.
BD = 12cm.
Đáp án : C
Dựa vào kiến thức về hình vuông: hình vuông có hai đường chéo bằng nhau.
Vì ABCD là hình vuông nên BD = AC = 11 cm.
Đáp án C.
Hình bình hành không có tính chất nào sau đây?
Hai cạnh đối song song với nhau.
Hai cạnh đối bằng nhau.
Bốn cạnh bằng nhau.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Đáp án : C
Hình bình hành có:
- Hai cặp cạnh đối diện song song và bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Bốn cạnh của hình bình hành không bằng nhau nên khẳng định C sai.
Đáp án C.
Hội nghị lần thứ 10 Ban Chấp hành Trung ương Đảng khóa XIII họp từ ngày 18/9 đến ngày 20/9/2024 tại Thủ đô Hà Nội để xem xét thảo luận, cho ý kiến các tờ trình, đề án, báo cáo của Bộ Chính trị liên quan một số vấn đề lớn, cơ bản và quan trọng.

Em hãy cho biết:
- Số La Mã XIII đề cập phía trên có giá trị là bao nhiêu trong hệ thập phân?
- Số 3; 9 được viết ở dạng số La Mã như thế nào?
Dựa vào kiến thức về cách viết số La Mã.
- Số XIII có 4 thành phần là X, I, I, I tương ứng với các giá trị 10,1,1,1. Do đó biểu diễn số
10 + 1 + 1 + 1 = 13.
- Số 3 được viết là III; số 9 được viết là IX.
Thực hiện các phép tính sau:
a) \(52.26 + 52.74\)
b) \({3^2}.2 - {7^{10}}:{7^9} + {2024^0}\)
c) \(107 - \left\{ {38 + \left[ {{{7.3}^2} - 24:6 + {{\left( {9 - 7} \right)}^3}} \right]} \right\}:15\)
a) Sử dụng tính chất phân phối của phép nhân đối với phép cộng.
b) Nếu phép tính có cả cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.
c) Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
a) \(52.26 + 52.74\)
\(\begin{array}{l} = 52.\left( {26 + 74} \right)\\ = 52.100\\ = 5200\end{array}\)
b) \({3^2}.2 - {7^{10}}:{7^9} + {2024^0}\)
\( = 9.2 - {7^1} + 1\)
\( = 18 - 7 + 1\)
\( = 12\)
c) \(107 - \left\{ {38 + \left[ {{{7.3}^2} - 24:6 + {{\left( {9 - 7} \right)}^3}} \right]} \right\}:15\)
\( = \;107 - \{ \;38 + [\;7.9 - 24:6 + {2^3}]\} \;:15\)
\( = 107 - \left\{ {38 + \left[ {63 - 4 + 8} \right]} \right\}:15\)
\( = 107 - \left\{ {38 + 67} \right\}:15\)
\( = 107 - 105:15\)
\( = 107 - 7\)
\( = 100\)
Tìm x, biết
a) \(12x - 33 = {3^2}{.3^3}\)
b) \(2\left( {x - 51} \right) = {2.2^3} + 20\)
Sử dụng quy tắc chuyển vế kết hợp với các phép tính để tìm x.
a) \(12x - 33 = {3^2}{.3^3}\)
\(12x - 33 = 9.27\;\;\)
\(12x - 33 = \;243\;\;\)
\(12x = 243 + 33\)
\(12x = 276\)
\(x = 276:12\)
\(x = \;23\;\)
Vậy \(x = 23\).
b) \(2\left( {x - 51} \right) = {2.2^3} + 20\)
\(\;2\left( {x - 51} \right) = 16 + 20\)
\(2\left( {x - 51} \right) = 36\)
\(x\; - 51 = 36:2\)
\(x\; - 51 = 18\)
\(\;x = 18 + 51\)
\(x = 69\)
Vậy \(x = 69\).
Mỗi người khi ăn sẽ hấp thụ ca - lo và khi hoạt động thì sẽ tiêu hao ca - lo. Bạn Minh thống kê số ca - lo hằng ngày của mình, em hãy giúp bạn Minh tính tổng số ca – lo còn lại sau khi ăn sáng và thực hiện các hoạt động như bảng bên.

Tổng số ca-lo còn lại bằng ca–lo hấp thụ cộng ca-lo tiêu hao.
Tổng số ca – lo còn lại sau khi ăn sáng và thực hiện các hoạt động là:
\(290 + 189 + 110 - 70 - 130 = 389\).
Cho hai hình vẽ bêna) Tính diện tích của hình thoi ABCD và diện tích của hình chữ nhật MNPQ.b) Diện tích của hình chữ nhật MNPQ gấp mấy lần diện tích của hình thoi ABCD.
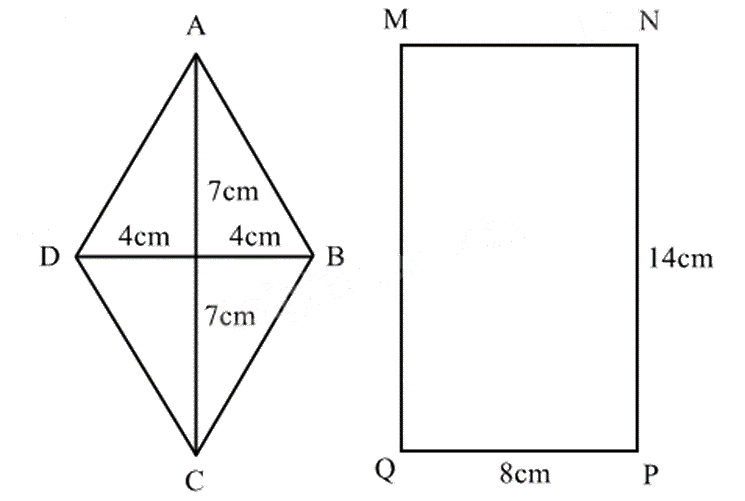
Sử dụng công thức tính diện tích hình chữ nhật, diện tích hình thoi.
Diện tích hình chữ nhật = chiều dài . chiều rộng.
Diện tích hình thoi = \(\frac{1}{2}\). tích hai đường chéo.
a) Độ dài đường chéo AC là:
\(7 + 7 = 14\left( {cm} \right)\)
Độ dài đường chéo BD là:
\(4 + 4 = 8\left( {cm} \right)\)
Diện tích hình thoi ABCD là:
\(\left( {14.8} \right):2 = 56\left( {c{m^2}} \right)\)
Diện tích hình chữ nhật MNPQ là:
\(14.8 = 112\left( {c{m^2}} \right)\)
b) Vì \(56 = 112:2\) nên diện tích của hinh chữ nhật MNPQ gấp đôi diện tích hình thoi ABCD.
Chứng minh rằng \(A = {20^{20}} + {20^{21}} + {20^{22}} + {20^{23}} + ..... + {20^{70}} + {20^{71}}\) chia hết cho 21.
Sử dụng tính chất chia hết của một tổng.
Ta có:
\(\begin{array}{l}A = \left( {{{20}^{20}} + {{20}^{21}}} \right) + \left( {{{20}^{22}} + {{20}^{23}}} \right) + ..... + \left( {{{20}^{70}} + {{20}^{71}}} \right)\\ = {20^{20}}\left( {1 + 20} \right) + {20^{22}}\left( {1 + 20} \right) + ..... + {20^{70}}\left( {1 + 20} \right)\\ = 21\left( {{{20}^{20}} + {{20}^{22}} + ... + {{20}^{70}}} \right)\end{array}\)
Vì \(21 \vdots 21\) nên \(21\left( {{{20}^{20}} + {{20}^{22}} + ... + {{20}^{70}}} \right) \vdots 21\) hay \(A \vdots 21\).
Vậy \(A\) chia hết cho 21.
Đề thi giữa kì 1 Toán 6 - Đề số 18 thường bao gồm các dạng bài tập thuộc các chủ đề chính đã học trong nửa học kì đầu tiên. Các chủ đề này thường xoay quanh các kiến thức về số tự nhiên, phép tính với số tự nhiên, các khái niệm về tập hợp, và các bài toán ứng dụng đơn giản.
Cấu trúc đề thi thường được chia thành các phần:
Để giúp các em học sinh có sự chuẩn bị tốt nhất, chúng ta sẽ đi sâu vào phân tích chi tiết nội dung đề thi giữa kì 1 Toán 6 - Đề số 18. Dưới đây là một số dạng bài tập thường gặp:
Đây là phần kiến thức nền tảng, thường xuất hiện trong các đề thi. Các dạng bài tập có thể bao gồm:
Phần này tập trung vào việc rèn luyện kỹ năng thực hiện các phép tính một cách chính xác và nhanh chóng. Các dạng bài tập thường gặp:
Kiến thức về tập hợp giúp học sinh hiểu rõ hơn về cách phân loại và sắp xếp các đối tượng. Các dạng bài tập thường gặp:
Đây là phần bài tập giúp học sinh vận dụng kiến thức đã học vào giải quyết các vấn đề thực tế. Các dạng bài tập thường gặp:
Để đạt kết quả tốt nhất trong kỳ thi, các em học sinh cần có phương pháp ôn tập và làm bài khoa học. Dưới đây là một số lời khuyên:
Ngoài đề thi giữa kì 1 Toán 6 - Đề số 18, các em học sinh có thể tham khảo thêm các tài liệu ôn tập sau:
Đề thi giữa kì 1 Toán 6 - Đề số 18 là một cơ hội tốt để các em học sinh đánh giá năng lực và chuẩn bị cho các kỳ thi tiếp theo. Hãy ôn tập kỹ lưỡng và tự tin làm bài để đạt kết quả tốt nhất!