Chào mừng các em học sinh đến với đề thi giữa kì 2 Toán 6 - Đề số 4 chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì 2.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học và nâng cao khả năng giải toán.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. D | 2. D | 3. B | 4. D |
Câu 1
Phương pháp:
\(BC = AB + AC\)
Cách giải:
Vì A nằm giữa B và C nên \(BC = AB + AC\)
Vậy độ dài đoạn thẳng BC là: \(3 + 2 = 5\left( {cm} \right)\)
Chọn D.
Câu 2
Phương pháp:
Muốn tìm \(\dfrac{m}{n}\) của một số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\left( {m,n \in N,n \ne 0} \right)\) .
Cách giải: \(\dfrac{3}{4}\) của \(60\)là: \(\dfrac{3}{4} \times 60 = 45\)
Chọn D.
Câu 3
Phương pháp:
Quy đồng mẫu các phân số rồi thực hiện cộng các phân số cùng mẫu với nhau.
Quy đồng mẫu số nhiều phân số với mẫu dương ta làm như sau :
Bước 1 : Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.
Bước 2 : Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3 : Nhân tử và mẫu của phân số với thừa số phụ tương ứng.
Cách giải:
\(\dfrac{1}{5} - \dfrac{1}{4} + \dfrac{1}{{20}} = \dfrac{4}{{20}} - \dfrac{5}{{20}} + \dfrac{1}{{20}} = \dfrac{{4 - 5 + 1}}{{20}} = 0\)
Chọn B
Câu 4
Phương pháp:
- Áp dụng nhận xét: Trên tia\(Ox,{\rm{ }}OM = a,{\rm{ }}ON = b\) , nếu \(0 < a < b\) thì điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
- Áp dụng tính chất: Nếu điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì\(AM + MB = AB\).
Cách giải:

Trên tia \(Ax\) ta có \(AC < AB\left( {do3cm < 8cm} \right)\) nên điểm \(C\) là điểm nằm giữa hai điểm \(A\) và \(B\)
\(\begin{array}{l} \Rightarrow AC + CB = AB\\ \Rightarrow CB = AB - AC = 8 - 3 = 5\left( {cm} \right)\end{array}\)
Vậy độ dài đoạn thẳng \(BC\) là \(5cm\).
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp
a) Viết ba phân số về cùng mẫu số rồi thực hiện phép tính cộng các phân số cùng mẫu số: ta cộng tử với tử mẫu giữ nguyên: \(\dfrac{a}{m} + \dfrac{b}{m} + \dfrac{c}{m} = \dfrac{{a + b + c}}{m}\)
b) Chuyển hỗn số về phân số rồi thực hiện chia hai phân số: \(\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c}\)
c) Nhóm \(\left( {\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{{ - 7}}{{11}}.\dfrac{8}{{19}}} \right) + \dfrac{{ - 4}}{{11}}\) , rồi thực hiện phép tính trong ngoặc trước. Để thực hiện phép tính trong ngoặc ta biến đổi chúng thành một số nhân với một tổng: \(\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{{ - 7}}{{11}}.\dfrac{8}{{19}} = \dfrac{{ - 7}}{{11}}.\left( {\dfrac{{11}}{{19}} + \dfrac{8}{{11}}} \right)\)
Kiến thức sử dụng: Tính chất phân phối của phép nhân đối với phép cộng: \(a.b + a.c = a.\left( {b + c} \right)\)
Cách giải:
\(\begin{array}{l}a)\dfrac{{ - 7}}{9} + \dfrac{5}{{12}} - \dfrac{{11}}{{18}}\\ = \dfrac{{ - 7.4}}{{36}} + \dfrac{{5.3}}{{36}} - \dfrac{{11.2}}{{36}}\\ = \dfrac{{ - 28}}{{36}} + \dfrac{{15}}{{36}} - \dfrac{{22}}{{36}}\\ = \dfrac{{ - 28 + 15 - 22}}{{36}}\\ = \dfrac{{ - 35}}{{36}}\end{array}\)
\(b)2\dfrac{2}{7}:\dfrac{{ - 32}}{{35}} = \dfrac{{16}}{7}:\dfrac{{ - 32}}{{35}} = \dfrac{{16}}{7}.\dfrac{{ - 35}}{{32}} = \dfrac{{ - 5}}{2}\)
\(\begin{array}{l}c)\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}} + \dfrac{{ - 4}}{{11}} = \left( {\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}}} \right) + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 7}}{{11}}.\left( {\dfrac{{11}}{{19}} + \dfrac{8}{{19}}} \right) + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 7}}{{11}}.1 + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 11}}{{11}}\\ = - 1\end{array}\)
Bài 2:
Phương pháp:
a) Chuyển \(\dfrac{7}{9}\) từ vế trái sang vế phải đổi dấu thành \(\dfrac{{ - 7}}{9}\) , rồi thực hiện phép tính ở bên vế phải, ta tìm được x.
b) Chuyển hỗn số về dạng phân số. Để tìm x ta nhân phân số ở bên vế phải với \(\dfrac{{ - 21}}{{20}}\).
c) Chuyển \( - 1\) ở vế trái sang vế phải đổi dấu thành \( + 1\) rồi thực hiện phép tính bên vế phải. Để tìm x ta lấy kết quả phép tính vừa tính bên vế phải chia cho \(\dfrac{5}{6}\).
Cách giải:
\(\begin{array}{l}a)x + \dfrac{7}{9} = - \dfrac{5}{6}\\x = \dfrac{{ - 5}}{6} - \dfrac{7}{9}\\x = \dfrac{{ - 15}}{{18}} - \dfrac{{14}}{{18}}\\x = \dfrac{{ - 29}}{{18}}\end{array}\)
Vậy \(x = \dfrac{{ - 29}}{{18}}\)
\(\begin{array}{l}b)x:\dfrac{{ - 21}}{{20}} = 2\dfrac{1}{7}\\x:\dfrac{{ - 21}}{{20}} = \dfrac{{15}}{7}\\x = \dfrac{{15}}{7}.\dfrac{{ - 21}}{{20}}\\x = \dfrac{{3.5}}{7}.\dfrac{{\left( { - 3} \right).7}}{{4.5}}\\x = \dfrac{{ - 9}}{4}\end{array}\)
Vậy \(x = \dfrac{{ - 9}}{4}\)
\(\begin{array}{l}c)\dfrac{5}{6}x - 1 = - \dfrac{2}{3}\\\dfrac{5}{6}x = \dfrac{{ - 2}}{3} + 1\\\dfrac{5}{6}x = \dfrac{1}{3}\\x = \dfrac{1}{3}:\dfrac{5}{6}\\x = \dfrac{1}{3}.\dfrac{6}{5}\\x = \dfrac{2}{5}\end{array}\)
Vậy \(x = \dfrac{2}{5}\)
Bài 3
Phương pháp:
Áp dụng các quy tắc:
- Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}(m,n \in \mathbb{N},n \ne 0)\).
- Muốn tìm tỉ số phần trăm của hai số \(a\) và \(b\), ta tìm thương của hai số viết dưới dạng số thập phân sau đó nhân thương vừa tìm được với \(100\) được kết quả ta viết thêm kí hiệu \(\% \)vào bên phải.
Cách giải:
a) Số học sinh lựa chọn đi Đầm Long là: \(45.\dfrac{1}{3} = 15\) (học sinh)
Số học sinh không lựa chọn đi Đầm Long là: \(45 - 15 = 30\) (học sinh)
Số học sinh lựa chọn đi Khoang Xanh là: \(30.\dfrac{2}{3} = 20\) (học sinh)
Số học sinh lựa chọn đi Đảo Ngọc Xanh là: \(30 - 20 = 10\) (học sinh)
Vậy địa điểm mà các bạn lựa chọn đi nhiều nhất là Khoang Xanh.
b) Tỉ số phần trăm của số học sinh chọn đi Đảo Ngọc Xanh so với số học sinh cả lớp là:
\(10:45 \times 100 = 22,22\% \)
Đáp số: a) Khoang Xanh; b) 22,22%
Bài 4
Phương pháp:
a) Vẽ hình, so sánh độ dài hai đoạn OA và OB.
b) Áp dụng tính chất của điểm nằm giữa hai điểm.
c) Áp dụng tính chất của trung điểm của đoạn thẳng.
Cách giải:
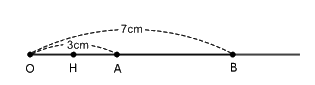
a)
Vì A và B nằm cùng phía so với điểm O mà OA < OB
Nên điểm A nằm giữa hai điểm O và B.
b)
Vì điểm A nằm giữa hai điểm O và B nên ta có: \(OA + AB = OB\)
Hay \(3 + AB = 7\)
Suy ra: \(AB = 7 - 3 = 4\left( {cm} \right)\)
c)
Vì H là trung điểm của đoạn thẳng OA nên \(HA = \dfrac{{OA}}{2} = \dfrac{4}{2} = 2\left( {{\rm{cm}}} \right)\)
Vì A nằm giữa H và B nên \(HB = HA + AB = 2 + 4 = 6\left( {{\rm{cm}}} \right)\)
Bài 5
Phương pháp:
Thu gọn vế trái rồi tìm \(x\).
Cách giải:
Ta có:
\(\begin{array}{l}\dfrac{1}{{2.4}} + \dfrac{1}{{4.6}} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2).2x}} = \dfrac{1}{8}\\\dfrac{1}{2}.\left( {\dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{4} - \dfrac{1}{6} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2)}} - \dfrac{1}{{2x}}} \right) = \dfrac{1}{8}\\\dfrac{1}{2}.\left( {\dfrac{1}{2} - \dfrac{1}{{2x}}} \right) = \dfrac{1}{8}\\\dfrac{1}{2} - \dfrac{1}{{2x}} = \dfrac{1}{8}:\dfrac{1}{2}\end{array}\)
\(\begin{array}{l}\dfrac{1}{2} - \dfrac{1}{{2x}} = \dfrac{1}{4}\\\dfrac{1}{{2x}} = \dfrac{1}{2} - \dfrac{1}{4}\\\dfrac{1}{{2x}} = \dfrac{1}{4}\\ \Rightarrow 2x = 4\\ \Rightarrow x = 2\end{array}\)
Vậy \(x = 2\).
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho hình vẽ, đoạn thẳng BC có độ dài bằng:
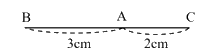
A. 3cm
B. 2cm
C. 4cm
D. 5cm
Câu 2:\(\dfrac{3}{4}\) của \(60\) là:
A.\(50\)
B.\(30\)
C.\(40\)
D.\(45\)
Câu 3: Kết quả phép tính \(\dfrac{1}{5} - \dfrac{1}{4} + \dfrac{1}{{20}}\) là :
A.\(10\)
B.\(0\)
C.\(\dfrac{{ - 1}}{{10}}\)
D.\(\dfrac{1}{{10}}\)
Câu 4:Trên tia \(Ax\) lấy hai điểm \(B\) và \(C\) sao cho \(AC = 3cm,\,\,AB = 8cm\). Khi đó độ dài của đoạn thẳng \(BC\) bằng
A. \(11\)
B. \(11cm\)
C. \(5\)
D. \(5cm\)
Phần II. Tự luận (8 điểm):
Bài 1: (1,5 điểm) Thực hiện phép tính:
\(a)\,\dfrac{{ - 7}}{9} + \dfrac{5}{{12}} - \dfrac{{11}}{{18}}\)
\(b)\,2\dfrac{2}{7}:\dfrac{{ - 32}}{{35}}\)
\(c)\,\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}} + \dfrac{{ - 4}}{{11}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\(a)\,x + \dfrac{7}{9} = - \dfrac{5}{6}\)
\(b)\,x:\dfrac{{ - 21}}{{20}} = 2\dfrac{1}{7}\)
\(c)\,\dfrac{5}{6}x - 1 = - \dfrac{2}{3}\)
Bài 3 (2 điểm) Lớp 6A có \(45\) học sinh. Trong giờ sinh hoạt lớp, để chuẩn bị cho buổi dã ngoại tổng kết năm học, cô giáo chủ nhiệm đã khảo sát địa điểm dã ngoại em yêu thích với ba khu du lịch sinh thái: Đầm Long, Khoang Xanh, Đảo Ngọc Xanh. Kết quả thu được như sau: \(\dfrac{1}{3}\) số học sinh cả lớp lựa chọn đi Đầm Long, số học sinh lựa chọn đi Khoang Xanh bằng \(\dfrac{2}{3}\) số học sinh còn lại.
a) Địa điểm nào được các bạn học sinh lớp 6A lựa chọn đi đông nhất?
b) Tính tỉ số phần trăm của số học sinh chọn đi Đảo Ngọc Xanh so với số học sinh cả lớp.
Bài 4: (2,5 điểm) Trên tia Ox lấy hai điểm A và B sao cho OA = 3cm, OB = 7cm.
a) Trong ba điểm O, A, B điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) Tính độ dài đoạn thẳng AB.
c) Gọi H là trung điểm của OA. Tính độ dài đoạn thẳng HB.
Bài 5:(0,5 điểm)Tìm \(x\) , biết: \(\dfrac{1}{{2.4}} + \dfrac{1}{{4.6}} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2).2x}} = \dfrac{1}{8}\,\,\,\,\,\,\,\,\,\,\,\,\,(x \in \mathbb{N},\,\,x \ge 2)\)
Phần I: Trắc nghiệm
1. D | 2. D | 3. B | 4. D |
Câu 1
Phương pháp:
\(BC = AB + AC\)
Cách giải:
Vì A nằm giữa B và C nên \(BC = AB + AC\)
Vậy độ dài đoạn thẳng BC là: \(3 + 2 = 5\left( {cm} \right)\)
Chọn D.
Câu 2
Phương pháp:
Muốn tìm \(\dfrac{m}{n}\) của một số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\left( {m,n \in N,n \ne 0} \right)\) .
Cách giải: \(\dfrac{3}{4}\) của \(60\)là: \(\dfrac{3}{4} \times 60 = 45\)
Chọn D.
Câu 3
Phương pháp:
Quy đồng mẫu các phân số rồi thực hiện cộng các phân số cùng mẫu với nhau.
Quy đồng mẫu số nhiều phân số với mẫu dương ta làm như sau :
Bước 1 : Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.
Bước 2 : Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3 : Nhân tử và mẫu của phân số với thừa số phụ tương ứng.
Cách giải:
\(\dfrac{1}{5} - \dfrac{1}{4} + \dfrac{1}{{20}} = \dfrac{4}{{20}} - \dfrac{5}{{20}} + \dfrac{1}{{20}} = \dfrac{{4 - 5 + 1}}{{20}} = 0\)
Chọn B
Câu 4
Phương pháp:
- Áp dụng nhận xét: Trên tia\(Ox,{\rm{ }}OM = a,{\rm{ }}ON = b\) , nếu \(0 < a < b\) thì điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
- Áp dụng tính chất: Nếu điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì\(AM + MB = AB\).
Cách giải:

Trên tia \(Ax\) ta có \(AC < AB\left( {do3cm < 8cm} \right)\) nên điểm \(C\) là điểm nằm giữa hai điểm \(A\) và \(B\)
\(\begin{array}{l} \Rightarrow AC + CB = AB\\ \Rightarrow CB = AB - AC = 8 - 3 = 5\left( {cm} \right)\end{array}\)
Vậy độ dài đoạn thẳng \(BC\) là \(5cm\).
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp
a) Viết ba phân số về cùng mẫu số rồi thực hiện phép tính cộng các phân số cùng mẫu số: ta cộng tử với tử mẫu giữ nguyên: \(\dfrac{a}{m} + \dfrac{b}{m} + \dfrac{c}{m} = \dfrac{{a + b + c}}{m}\)
b) Chuyển hỗn số về phân số rồi thực hiện chia hai phân số: \(\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c}\)
c) Nhóm \(\left( {\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{{ - 7}}{{11}}.\dfrac{8}{{19}}} \right) + \dfrac{{ - 4}}{{11}}\) , rồi thực hiện phép tính trong ngoặc trước. Để thực hiện phép tính trong ngoặc ta biến đổi chúng thành một số nhân với một tổng: \(\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{{ - 7}}{{11}}.\dfrac{8}{{19}} = \dfrac{{ - 7}}{{11}}.\left( {\dfrac{{11}}{{19}} + \dfrac{8}{{11}}} \right)\)
Kiến thức sử dụng: Tính chất phân phối của phép nhân đối với phép cộng: \(a.b + a.c = a.\left( {b + c} \right)\)
Cách giải:
\(\begin{array}{l}a)\dfrac{{ - 7}}{9} + \dfrac{5}{{12}} - \dfrac{{11}}{{18}}\\ = \dfrac{{ - 7.4}}{{36}} + \dfrac{{5.3}}{{36}} - \dfrac{{11.2}}{{36}}\\ = \dfrac{{ - 28}}{{36}} + \dfrac{{15}}{{36}} - \dfrac{{22}}{{36}}\\ = \dfrac{{ - 28 + 15 - 22}}{{36}}\\ = \dfrac{{ - 35}}{{36}}\end{array}\)
\(b)2\dfrac{2}{7}:\dfrac{{ - 32}}{{35}} = \dfrac{{16}}{7}:\dfrac{{ - 32}}{{35}} = \dfrac{{16}}{7}.\dfrac{{ - 35}}{{32}} = \dfrac{{ - 5}}{2}\)
\(\begin{array}{l}c)\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}} + \dfrac{{ - 4}}{{11}} = \left( {\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}}} \right) + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 7}}{{11}}.\left( {\dfrac{{11}}{{19}} + \dfrac{8}{{19}}} \right) + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 7}}{{11}}.1 + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 11}}{{11}}\\ = - 1\end{array}\)
Bài 2:
Phương pháp:
a) Chuyển \(\dfrac{7}{9}\) từ vế trái sang vế phải đổi dấu thành \(\dfrac{{ - 7}}{9}\) , rồi thực hiện phép tính ở bên vế phải, ta tìm được x.
b) Chuyển hỗn số về dạng phân số. Để tìm x ta nhân phân số ở bên vế phải với \(\dfrac{{ - 21}}{{20}}\).
c) Chuyển \( - 1\) ở vế trái sang vế phải đổi dấu thành \( + 1\) rồi thực hiện phép tính bên vế phải. Để tìm x ta lấy kết quả phép tính vừa tính bên vế phải chia cho \(\dfrac{5}{6}\).
Cách giải:
\(\begin{array}{l}a)x + \dfrac{7}{9} = - \dfrac{5}{6}\\x = \dfrac{{ - 5}}{6} - \dfrac{7}{9}\\x = \dfrac{{ - 15}}{{18}} - \dfrac{{14}}{{18}}\\x = \dfrac{{ - 29}}{{18}}\end{array}\)
Vậy \(x = \dfrac{{ - 29}}{{18}}\)
\(\begin{array}{l}b)x:\dfrac{{ - 21}}{{20}} = 2\dfrac{1}{7}\\x:\dfrac{{ - 21}}{{20}} = \dfrac{{15}}{7}\\x = \dfrac{{15}}{7}.\dfrac{{ - 21}}{{20}}\\x = \dfrac{{3.5}}{7}.\dfrac{{\left( { - 3} \right).7}}{{4.5}}\\x = \dfrac{{ - 9}}{4}\end{array}\)
Vậy \(x = \dfrac{{ - 9}}{4}\)
\(\begin{array}{l}c)\dfrac{5}{6}x - 1 = - \dfrac{2}{3}\\\dfrac{5}{6}x = \dfrac{{ - 2}}{3} + 1\\\dfrac{5}{6}x = \dfrac{1}{3}\\x = \dfrac{1}{3}:\dfrac{5}{6}\\x = \dfrac{1}{3}.\dfrac{6}{5}\\x = \dfrac{2}{5}\end{array}\)
Vậy \(x = \dfrac{2}{5}\)
Bài 3
Phương pháp:
Áp dụng các quy tắc:
- Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}(m,n \in \mathbb{N},n \ne 0)\).
- Muốn tìm tỉ số phần trăm của hai số \(a\) và \(b\), ta tìm thương của hai số viết dưới dạng số thập phân sau đó nhân thương vừa tìm được với \(100\) được kết quả ta viết thêm kí hiệu \(\% \)vào bên phải.
Cách giải:
a) Số học sinh lựa chọn đi Đầm Long là: \(45.\dfrac{1}{3} = 15\) (học sinh)
Số học sinh không lựa chọn đi Đầm Long là: \(45 - 15 = 30\) (học sinh)
Số học sinh lựa chọn đi Khoang Xanh là: \(30.\dfrac{2}{3} = 20\) (học sinh)
Số học sinh lựa chọn đi Đảo Ngọc Xanh là: \(30 - 20 = 10\) (học sinh)
Vậy địa điểm mà các bạn lựa chọn đi nhiều nhất là Khoang Xanh.
b) Tỉ số phần trăm của số học sinh chọn đi Đảo Ngọc Xanh so với số học sinh cả lớp là:
\(10:45 \times 100 = 22,22\% \)
Đáp số: a) Khoang Xanh; b) 22,22%
Bài 4
Phương pháp:
a) Vẽ hình, so sánh độ dài hai đoạn OA và OB.
b) Áp dụng tính chất của điểm nằm giữa hai điểm.
c) Áp dụng tính chất của trung điểm của đoạn thẳng.
Cách giải:
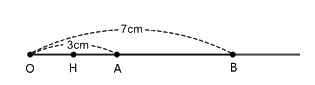
a)
Vì A và B nằm cùng phía so với điểm O mà OA < OB
Nên điểm A nằm giữa hai điểm O và B.
b)
Vì điểm A nằm giữa hai điểm O và B nên ta có: \(OA + AB = OB\)
Hay \(3 + AB = 7\)
Suy ra: \(AB = 7 - 3 = 4\left( {cm} \right)\)
c)
Vì H là trung điểm của đoạn thẳng OA nên \(HA = \dfrac{{OA}}{2} = \dfrac{4}{2} = 2\left( {{\rm{cm}}} \right)\)
Vì A nằm giữa H và B nên \(HB = HA + AB = 2 + 4 = 6\left( {{\rm{cm}}} \right)\)
Bài 5
Phương pháp:
Thu gọn vế trái rồi tìm \(x\).
Cách giải:
Ta có:
\(\begin{array}{l}\dfrac{1}{{2.4}} + \dfrac{1}{{4.6}} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2).2x}} = \dfrac{1}{8}\\\dfrac{1}{2}.\left( {\dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{4} - \dfrac{1}{6} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2)}} - \dfrac{1}{{2x}}} \right) = \dfrac{1}{8}\\\dfrac{1}{2}.\left( {\dfrac{1}{2} - \dfrac{1}{{2x}}} \right) = \dfrac{1}{8}\\\dfrac{1}{2} - \dfrac{1}{{2x}} = \dfrac{1}{8}:\dfrac{1}{2}\end{array}\)
\(\begin{array}{l}\dfrac{1}{2} - \dfrac{1}{{2x}} = \dfrac{1}{4}\\\dfrac{1}{{2x}} = \dfrac{1}{2} - \dfrac{1}{4}\\\dfrac{1}{{2x}} = \dfrac{1}{4}\\ \Rightarrow 2x = 4\\ \Rightarrow x = 2\end{array}\)
Vậy \(x = 2\).
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho hình vẽ, đoạn thẳng BC có độ dài bằng:
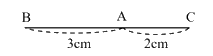
A. 3cm
B. 2cm
C. 4cm
D. 5cm
Câu 2:\(\dfrac{3}{4}\) của \(60\) là:
A.\(50\)
B.\(30\)
C.\(40\)
D.\(45\)
Câu 3: Kết quả phép tính \(\dfrac{1}{5} - \dfrac{1}{4} + \dfrac{1}{{20}}\) là :
A.\(10\)
B.\(0\)
C.\(\dfrac{{ - 1}}{{10}}\)
D.\(\dfrac{1}{{10}}\)
Câu 4:Trên tia \(Ax\) lấy hai điểm \(B\) và \(C\) sao cho \(AC = 3cm,\,\,AB = 8cm\). Khi đó độ dài của đoạn thẳng \(BC\) bằng
A. \(11\)
B. \(11cm\)
C. \(5\)
D. \(5cm\)
Phần II. Tự luận (8 điểm):
Bài 1: (1,5 điểm) Thực hiện phép tính:
\(a)\,\dfrac{{ - 7}}{9} + \dfrac{5}{{12}} - \dfrac{{11}}{{18}}\)
\(b)\,2\dfrac{2}{7}:\dfrac{{ - 32}}{{35}}\)
\(c)\,\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}} + \dfrac{{ - 4}}{{11}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\(a)\,x + \dfrac{7}{9} = - \dfrac{5}{6}\)
\(b)\,x:\dfrac{{ - 21}}{{20}} = 2\dfrac{1}{7}\)
\(c)\,\dfrac{5}{6}x - 1 = - \dfrac{2}{3}\)
Bài 3 (2 điểm) Lớp 6A có \(45\) học sinh. Trong giờ sinh hoạt lớp, để chuẩn bị cho buổi dã ngoại tổng kết năm học, cô giáo chủ nhiệm đã khảo sát địa điểm dã ngoại em yêu thích với ba khu du lịch sinh thái: Đầm Long, Khoang Xanh, Đảo Ngọc Xanh. Kết quả thu được như sau: \(\dfrac{1}{3}\) số học sinh cả lớp lựa chọn đi Đầm Long, số học sinh lựa chọn đi Khoang Xanh bằng \(\dfrac{2}{3}\) số học sinh còn lại.
a) Địa điểm nào được các bạn học sinh lớp 6A lựa chọn đi đông nhất?
b) Tính tỉ số phần trăm của số học sinh chọn đi Đảo Ngọc Xanh so với số học sinh cả lớp.
Bài 4: (2,5 điểm) Trên tia Ox lấy hai điểm A và B sao cho OA = 3cm, OB = 7cm.
a) Trong ba điểm O, A, B điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) Tính độ dài đoạn thẳng AB.
c) Gọi H là trung điểm của OA. Tính độ dài đoạn thẳng HB.
Bài 5:(0,5 điểm)Tìm \(x\) , biết: \(\dfrac{1}{{2.4}} + \dfrac{1}{{4.6}} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2).2x}} = \dfrac{1}{8}\,\,\,\,\,\,\,\,\,\,\,\,\,(x \in \mathbb{N},\,\,x \ge 2)\)
Đề thi giữa kì 2 Toán 6 - Đề số 4 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ hiểu và vận dụng kiến thức đã học trong giai đoạn giữa học kì 2. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số nguyên, phân số, tỉ số, phần trăm và hình học cơ bản.
Thông thường, đề thi giữa kì 2 Toán 6 - Đề số 4 sẽ có cấu trúc tương tự như sau:
Để giúp các em học sinh ôn tập hiệu quả, chúng ta sẽ đi vào phân tích chi tiết nội dung của đề thi giữa kì 2 Toán 6 - Đề số 4:
Phần này thường tập trung vào các kiến thức về:
Phần này thường tập trung vào các kiến thức về:
Phần này thường tập trung vào các kiến thức về:
Phần này thường tập trung vào các kiến thức về:
Để giúp các em học sinh giải quyết các bài tập trong đề thi một cách hiệu quả, chúng ta sẽ cung cấp hướng dẫn giải chi tiết cho từng bài tập. Các em có thể tham khảo các bước giải sau:
Ngoài đề thi giữa kì 2 Toán 6 - Đề số 4, các em học sinh có thể luyện tập thêm với các đề thi khác để nâng cao khả năng giải toán. Giaitoan.edu.vn cung cấp một kho đề thi Toán 6 phong phú, đa dạng, đáp ứng nhu cầu ôn tập của các em.
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi giữa kì 2 Toán 6!