Chào mừng các em học sinh lớp 6 đến với đề thi học kì 1 môn Toán - Đề số 13, chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 1.
Giaitoan.edu.vn cung cấp đề thi và lời giải chi tiết, giúp các em tự tin hơn trong kỳ thi sắp tới.
Cho tập hợp A = {1; 3; 9; 0; 4; 2}, số phần tử trong tập hợp A là:
Trong các số sau, số nào là số nguyên tố?
Số đối của – 3 là:
Kết quả của phép tính (- 30) : 2 là:
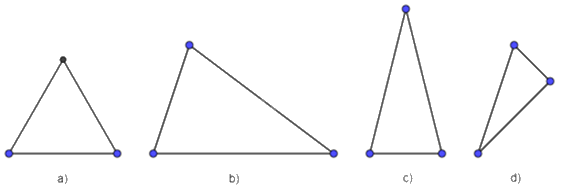
Trong các hình sau, hình nào là tam giác đều?
Trong hình chữ nhật, có:
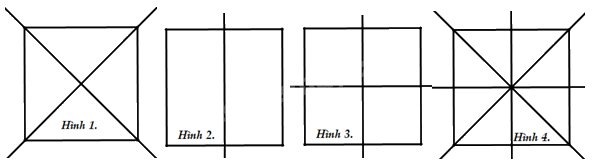
Hình nào dưới vẽ đúng trục đối xứng của hình vuông
Số lượng hình có tâm đối xứng là

Cho a = 32 . 2 . 5 và b = 24 . 3 . 7. Tìm ƯCLN của a và b.
Hãy sắp xếp các số sau theo thứ tự tăng dần: -3; 4; 7; -7; 0; -1.
Kết quả của phép tính (-80) + (-20) là:
Một chiếc tàu ngầm đang ở độ sâu 20 m, tàu tiếp tục lặn xuống thêm 15m nữa. Hỏi khi đó, tàu ngầm ở độ sâu bao nhiêu mét?
a) Liệt kê các số nguyên tố nhỏ hơn 9.
b) Sắp xếp các số nguyên sau theo thứ tự giảm dần: –11; 0; 8; –4; 12.
c) Viết tập hợp A gồm các số tự nhiên là ước của 8.
d) Liệt kê các số tự nhiên là bội của 5 nhỏ hơn 22.
e) Tìm số đối của –4; 0.
f) Cho tập hợp \(B = {\rm{\{ }}x \in Z\left| { - 3 < x < 2\} } \right.\). Viết tập hợp B dưới dạng liệt kê các phần tử?
a) Thực hiện phép tính: \(60:\left[ {15 - {{\left( {7 - 4} \right)}^2}} \right]\)
b) Tìm x, biết: x – 7 = -39
c) Mẹ bạn An mang 300 000 đồng vào siêu thị mua 2 kg táo, 5 kg gạo. Giá mỗi ki-lô-gam táo là 60 000 đồng, mỗi ki-lô-gam gạo là 20 000 đồng. Hỏi mẹ bạn An còn lại bao nhiêu tiền?
Dùng số nguyên thích hợp để mô tả mỗi tình huống sau:
a) Mực nước hồ chứa giảm xuống 3 m.
b) Có 15 000 000 đồng trong ngân hàng.
Hình thoi ABCD cạnh 5cm có tâm đối xứng O . Biết OA = 4cm, OB = 3cm.
a) Tính diện tích hình thoi.
b) So sánh chu vi và diện tích tam giác OAB và tam giác OCD.
Cho tập hợp A = {1; 3; 9; 0; 4; 2}, số phần tử trong tập hợp A là:
Đáp án : C
Đếm số phần tử trong tập hợp A.
Tập hợp A có 6 phần tử.
Trong các số sau, số nào là số nguyên tố?
Đáp án : B
Dựa vào kiến thức về số nguyên tố: Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó.
Ta có:
Ư(8) = {1; 2; 4; 8}
Ư(5) = {1; 5}
Ư(15) = {1; 3; 5; 15}
Ư(33) = {1; 3; 11; 33}
=> 5 là số nguyên tố.
Số đối của – 3 là:
Đáp án : A
Số đối của a là –a.
Số đối của – 3 là – (- 3) = 3.
Kết quả của phép tính (- 30) : 2 là:
Đáp án : B
Để chia hai số nguyên khác dấu ta làm như sau:
Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại
Bước 2: Tính thương của hai số nguyên dương nhận được ở Bước 1
Bước 3: Thêm dấu “-” trước kết quả nhận được ở Bước 2, ta có thương cần tìm.
Ta có (- 30) : 2 = - (30 : 2) = - 15.
Trong các hình sau, hình nào là tam giác đều?
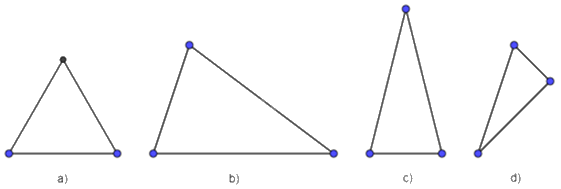
Đáp án : A
Tam giác đều có 3 cạnh bằng nhau.
Hình a là tam giác đều vì có 3 cạnh bằng nhau.
Trong hình chữ nhật, có:
Đáp án : D
Hình chữ nhật có:
- Hai cặp cạnh đối diện bằng nhau
- Hai cặp cạnh đối diện song song
- Bốn góc ở đỉnh bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Hình nào dưới vẽ đúng trục đối xứng của hình vuông
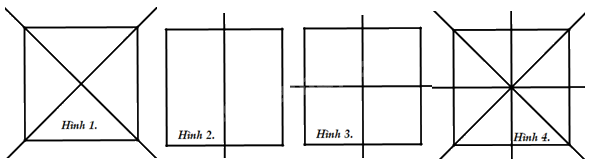
Đáp án : D
Dựa vào kiến thức về trục đối xứng của hình vuông.
Hình vuông có 4 trục đối xứng gồm 2 đường chéo của hình vuông và 2 đường thẳng đi qua trung điểm từng của cặp cạnh đối diện của hình vuông được vẽ ở hình 4.
Số lượng hình có tâm đối xứng là

Đáp án : A
Dựa vào kiến thức về tâm đối xứng: Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Trong các hình trên, các hình có tâm đối xứng là hai hình bông hoa.

Cho a = 32 . 2 . 5 và b = 24 . 3 . 7. Tìm ƯCLN của a và b.
Đáp án : A
Muốn tìm ƯCLN của của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau :
Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.
Bước 2 : Chọn ra các thừa số nguyên tố chung.
Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
Ta có: a = 32 . 2 . 5 và b = 24 . 3 . 7
Thừa số nguyên chung là 2 và 3.
=> ƯCLN(a, b) = 3 . 2.
Hãy sắp xếp các số sau theo thứ tự tăng dần: -3; 4; 7; -7; 0; -1.
Đáp án : A
Sử dụng quy tắc cộng hai số nguyên.
Các số nguyên âm là: -3; -7; -1.
Các số nguyên dương là 4; 7.
Vì 7 > 3 > 1 nên -7 < -3 < -1.
4 < 7
=> Các số sắp xếp theo thứ tự tăng dần là: – 7; - 3 ; - 1; 0 ; 4 ; 7.
Kết quả của phép tính (-80) + (-20) là:
Đáp án : D
Sử dụng quy tắc cộng hai số nguyên.
Ta có: (-80) + (-20) = - (80 + 20) = - 100
Một chiếc tàu ngầm đang ở độ sâu 20 m, tàu tiếp tục lặn xuống thêm 15m nữa. Hỏi khi đó, tàu ngầm ở độ sâu bao nhiêu mét?
Đáp án : B
Độ sâu của tàu ngầm được biểu diễn là số nguyên âm.
Lặn xuống được biểu diễn là số nguyên âm.
Tàu ngầm ở độ sâu 20m được biểu diễn là (−20).
Tàu ngầm lặn xuống thêm 15m được biểu diễn là (−15).
Độ sâu của tàu là: (−20) + (−15) = − (20 + 15) = − 35.
Vậy tàu ngầm ở độ sâu 35 mét.
a) Liệt kê các số nguyên tố nhỏ hơn 9.
b) Sắp xếp các số nguyên sau theo thứ tự giảm dần: –11; 0; 8; –4; 12.
c) Viết tập hợp A gồm các số tự nhiên là ước của 8.
d) Liệt kê các số tự nhiên là bội của 5 nhỏ hơn 22.
e) Tìm số đối của –4; 0.
f) Cho tập hợp \(B = {\rm{\{ }}x \in Z\left| { - 3 < x < 2\} } \right.\). Viết tập hợp B dưới dạng liệt kê các phần tử?
a) Sử dụng kiến thức về số nguyên tố.
b) - So sánh các số với 0.
- So sánh các số nguyên âm với nhau, các số nguyên dương với nhau.
c) Liệt kê các ước là số tự nhiên của 8.
d) Tìm bội của 5, chọn các số nhỏ hơn 22.
e) Số đối của a là – a.
f) Sử dụng cách viết tập hợp.
a) Các sô nguyên tố nhỏ hơn 9 là: 2; 3; 5; 7.
b) Các số nguyên âm là: - 11; -4. Vì 4 < 11 nên -4 > -11.
Các số nguyên dương là: 8; 12. Ta có 12 > 8.
Vậy các số nguyên sắp xếp theo thứ tự giảm dần là 12; 8; 0; -4; -11.
c) A = Ư(8) = {1 ; 2; 4; 8}.
d) Các số tự nhiên là bội của 5 nhỏ hơn 22: {0; 5 ; 10; 15; 20 }.
e) Số đối của –4 là – (- 4) = 4; số đối của 0 là 0.
f) \(B = {\rm{\{ }}x \in Z\left| { - 3 < x < 2\} } \right. = \left\{ {\, - 2;\, - 1;\,0;\,1} \right\}\)
a) Thực hiện phép tính: \(60:\left[ {15 - {{\left( {7 - 4} \right)}^2}} \right]\)
b) Tìm x, biết: x – 7 = -39
c) Mẹ bạn An mang 300 000 đồng vào siêu thị mua 2 kg táo, 5 kg gạo. Giá mỗi ki-lô-gam táo là 60 000 đồng, mỗi ki-lô-gam gạo là 20 000 đồng. Hỏi mẹ bạn An còn lại bao nhiêu tiền?
a) Sử dụng các quy tắc tính với số nguyên theo thứ tự thực hiện phép tính.
b) Sử dụng phép cộng với hai số nguyên khác dấu để tìm x.
c) Tính số tiền mẹ bạn An mua.
Số tiền mẹ bạn An còn lại bằng 300 000 – số tiền mẹ bạn An mua.
a) \(60:\left[ {15 - {{\left( {7 - 4} \right)}^2}} \right] = 60:\left[ {15 - {3^2}} \right] = 60:6 = 10\)
b) x – 7 = -39
x = -39 + 7
x = -32
Vậy x = -32.
c) Số tiền mẹ bạn An đã mua là: 2 . 60 000 + 5 . 20 000 = 220 000 (đồng).
Số tiền mẹ bạn An còn lại là: 300 000 – 220 000 = 80 000 (đồng).
Dùng số nguyên thích hợp để mô tả mỗi tình huống sau:
a) Mực nước hồ chứa giảm xuống 3 m.
b) Có 15 000 000 đồng trong ngân hàng.
Dựa vào ứng dụng của số nguyên trong thực tiễn.
a) -3
b) +15 000 000
Hình thoi ABCD cạnh 5cm có tâm đối xứng O . Biết OA = 4cm, OB = 3cm.
a) Tính diện tích hình thoi.
b) So sánh chu vi và diện tích tam giác OAB và tam giác OCD.
a) Dựa vào kiến thức về tâm đối xứng để tính diện tích hình thoi.
b) Tính chu vi tam giác OAB và chu vi tam giác OCD để so sánh.
Tính diện tích tam giác OAB và diện tích tam giác OCD để so sánh.
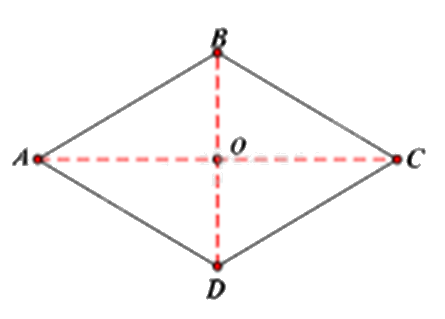
a) O là tâm đối xứng của hình thoi ABCD nên: O là trung điểm của đoạn AC và đoạn BD .
AC = 2.4 = 8cm; BD = 2.3 = 6cm.
Vì O là trung điểm của AC và BD nên OA = OC = 4cm; OB = OD = 3cm.
Diện tích của hình thoi ABCD là: \(\frac{1}{2}.AC.BD = \frac{1}{2}.8.6 = 24\left( {c{m^2}} \right)\)
b) + Chu vi tam giác OAB là: OA + OB + AB = 4 + 3 + 5 = 12 (cm).
Chu vi tam giác OCD là: OC + OD + CD = 4 + 3 + 5 = 12 (cm)
Suy ra chu vi của hai tam giác OAB và tam giác OCD bằng nhau.
+ Diện tích tam giác OAB là: \(\frac{1}{2}OA.OB = \frac{1}{2}4.3 = 6\left( {c{m^2}} \right)\).
Diện tích tam giác OCD là: \(\frac{1}{2}OC.OD = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\).
Suy ra diện tích của hai tam giác OAB và tam giác OCD bằng nhau.
Đề thi học kì 1 Toán 6 - Đề số 13 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, đòi hỏi học sinh phải có sự hiểu biết sâu sắc về các khái niệm và kỹ năng đã học.
Thông thường, đề thi học kì 1 Toán 6 - Đề số 13 - Kết nối tri thức sẽ bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để đạt kết quả tốt trong kỳ thi, học sinh cần:
Bài 1: Tính giá trị của biểu thức: 12 + 3 x 4 - 5
Lời giải:
12 + 3 x 4 - 5 = 12 + 12 - 5 = 24 - 5 = 19
Bài 2: Tìm số tự nhiên x sao cho x chia hết cho 3 và x < 15
Lời giải:
Các số tự nhiên chia hết cho 3 và nhỏ hơn 15 là: 0, 3, 6, 9, 12
Việc ôn tập kỹ lưỡng trước kỳ thi là vô cùng quan trọng. Học sinh nên dành thời gian để xem lại các bài giảng, làm lại các bài tập đã học và giải các đề thi thử. Điều này sẽ giúp các em tự tin hơn và đạt kết quả tốt nhất trong kỳ thi.
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, đề thi và lời giải chi tiết cho học sinh lớp 6. Chúng tôi cam kết mang đến cho các em một môi trường học tập hiệu quả và thú vị.
Hãy luôn giữ tinh thần học tập tích cực và chủ động. Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn. Chúc các em học tốt và đạt kết quả cao trong kỳ thi học kì 1!
| Chủ đề | Nội dung chính |
|---|---|
| Tập hợp | Khái niệm tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu) |
| Số tự nhiên | Các phép toán cộng, trừ, nhân, chia, tính chất của các phép toán |
| Phân số | Khái niệm phân số, các phép toán trên phân số, so sánh phân số |