Chào mừng các em học sinh lớp 6 đến với đề thi giữa kì 1 Toán 6 - Đề số 8 của giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì 1.
Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp các em làm quen với nhiều dạng câu hỏi thường gặp trong các bài kiểm tra.
Phần trắc nghiệm (4 điểm) Câu 1. Cho tập hợp M = {5;7;9;11}. Cách viết nào sau đây là đúng?
Phần trắc nghiệm (4 điểm)
Câu 1. Cho tập hợp M = {5;7;9;11}. Cách viết nào sau đây là đúng?
A. {5} \( \in \) M
B. 7\( \in \;\)M
C. 11 \( \notin \) M
D. \(\left\{ {9;11} \right\}\) \( \notin \) M
Câu 2. Cho các cách viết sau: A = { a, b, c, d}; B = {2; 13; 45}; C = (1; 2; 3); D = 1. Có bao nhiêu cách viết tập hợp là đúng trong các cách viết trên?
A. 1
B. 2
C. 3
D. 4
Câu 3. Các số La Mã XV, XXI được đọc lần lượt là:
A. mười lăm, hai mốt
B. mười năm, hai mốt
C. mười lăm, hai mươi mốt
D. mười bốn, mười chín
Câu 4. Tập hợp A các số tự nhiên có hai chữ số nhỏ hơn 15 là:
A. A = {10;11;12;13;14}
B. A = 11;12;13;14
C. A = {11;12;13;14}
D. A = {11;12;13;14;15}
Câu 5. Kết quả của phép tính 315 : 35 là:
A. 13
B. 320
C. 33
D. 310
Câu 6. Kết quả của phép tính 55.53 là:
A. 515
B. 58
C. 2515
D. 108
Câu 7. Lũy thừa 72 có giá trị bằng
A.14
B. 9
C. 49
D. 32
Câu 8. Số nào sau đây chia hết cho 2 và 3?
A.32
B. 42
C. 52
D. 62
Câu 9. Các số 2;17;37. Số nguyên tố là:
A. 2
B. 17
C. 37
D. cả 3 số trên
Câu 10. Số 780 được phân tích ra thừa số nguyên tố là:
A. 780 = 4.3.5.13
B. 780 = 22.15.13
C. 780 = 12.5.13
D. 780 = 22.3.5.13
Câu 11. Xét tập hợp N, trong các số sau, bội của 16 là
A. 28
B. 48
C. 36
D. 8
Câu 12. Trong phép chia cho 3 số dư có thể là:
A. 1;2;3
B. 0;1;2
C. 1;2
D. 0;1
Câu 13. Kết quả so sánh hai số 72 và 27 là?
A. 72 > 27
B. 72 ≥ 27
C. 72 = 27
D. 72 < 27
Câu 14. Chữ số x, y được thay vào số \(\overline {35x98y} \) để số đó chia hết cho 2;5 và 9 là:
A. x = 2; y = 0
B. x = 0; y = 2
C. x = 3, y = 8
D. x = 9; y = 0
Câu 15. Hiệu 11.9.5.2 – 48 chia hết cho
A. 2 và 3
B. 2 và 9
C. 3 và 5
D. 2 và 5
Câu 16. Quan sát các hình sau, hình bình hành là hình:

A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Câu 17. Cho tam giác đều ABC, biết AB = 3cm. Khi đó AC có độ dài là
A. 5cm
B. 4cm
C. 3cm
D. 2cm
Câu 18. Một mảnh vườn hình vuông có chiều dài cạnh là 24m. Khi đó chu vi mảnh vườn là:
A. 24m
B. 96m
C. 576m
D. 48m
Câu 19. Ghép 6 tam giác đều có độ dài cạnh là 5cm thành một lục giác đều. Khi đó độ dài đường chéo chính là:
A. 5cm.
B. 15cm.
C. 10cm.
D. 30cm.
Câu 20. Một miếng gỗ hình thoi có kích thước hai đường chéo lần lượt là 5cm; 8cm. Diện tích của miếng gỗ là:
A. 20cm2
B. 26cm2
C. 40cm2
D. 13cm2
Phần tự luận (6 điểm)
Bài 1(1,75 điểm): Tính:
a) 23.5 – 23.3
b) 125 - {2.[2.52 – (31 - 2.3)]} + 3.25
Bài 2 (1 điểm): Tìm số tự nhiên x, biết: (x – 11) . 4 = 43 : 2
Bài 3 (1 điểm):Khối 6 của một trường THCS có 143 học sinh đi tham quan. Biết một xe có 16 chỗ ngồi. Hỏi cần ít nhất bao nhiêu xe để chở hết số học sinh đó.
Bài 4 (1,25 điểm): Một khu vườn hình chữ nhật có diện tích 4500 m2, chiều rộng 50m, cửa vào khu vườn rộng 5m. Người ta muốn làm hàng rào xung quanh vườn bằng hai tầng dây thép gai. Hỏi cần phải dùng bao nhiêu mét dây thép gai để làm hàng rào?
Bài 5 (1 điểm): Cho B = 31 + 32 + 33 + ...+ 3300. Chứng minh rằng B chia hết cho 2
-------- Hết --------
Phần trắc nghiệm
Câu 1: B | Câu 2: A | Câu 3: C | Câu 4: A | Câu 5: D |
Câu 6: B | Câu 7: C | Câu 8: B | Câu 9: D | Câu 10: D |
Câu 11: B | Câu 12: B | Câu 13: D | Câu 14: A | Câu 15: A |
Câu 16: C | Câu 17: C | Câu 18: B | Câu 19: C | Câu 20: A |
Câu 1. Cho tập hợp M = {5;7;9;11}. Cách viết nào sau đây là đúng?
A. {5} \( \in \) M | B. 7\( \in \;\)M |
C. 11 \( \notin \) M | D. \(\left\{ {9;11} \right\}\) \( \notin \) M |
Phương pháp
Dựa vào cách viết tập hợp và phần tử.
Lời giải
{5}, \(\left\{ {9;11} \right\}\) là kí hiệu một tập hợp => không sử dụng dấu \( \in \) nên A và D sai.
7 \( \in \;\). M nên B đúng.
11 \( \in \). M nên C sai.
Đáp án B.
Câu 2. Cho các cách viết sau: A = {a, b, c, d}; B = {2; 13; 45}; C = (1; 2; 3); D = 1. Có bao nhiêu cách viết tập hợp là đúng trong các cách viết trên?
A. 1 | B. 2 |
C. 3 | D. 4 |
Phương pháp
Các phần tử của tập hợp được viết trong hai dấu ngoặc nhọn {}, cách nhau bởi dấu “;”.
Lời giải
Cách viết đúng là B = {2; 13; 45}
Vậy có 1 cách viết đúng.
Đáp án A.
Câu 3. Các số La Mã XV, XXI được đọc lần lượt là:
A. mười lăm, hai mốt | B. mười năm, hai mốt |
C. mười lăm, hai mươi mốt | D. mười bốn, mười chín |
Phương pháp
Dựa vào kiến thức về số La Mã.
Lời giải
Các số La Mã XV, XXI biểu diễn các số tự nhiên 15, 21 và được đọc lần lượt là: mười lăm, hai mươi mốt.
Đáp án C.
Câu 4. Tập hợp A các số tự nhiên có hai chữ số nhỏ hơn 15 là:
A. A = {10;11;12;13;14} | B. A = 11;12;13;14 |
C. A = {11;12;13;14} | D. A = {11;12;13;14;15} |
Phương pháp
Dựa vào cách mô ta một tập hợp.
Lời giải
Tập hợp các số tự nhiên có hai chữ số nhỏ hơn 15 là: A = {10;11;12;13;14}
Đáp án A.
Câu 5. Kết quả của phép tính 315 : 35 là:
A. 13 | B. 320 |
C. 33 | D. 310 |
Phương pháp
Dựa vào quy tắc chia lũy thừa cùng cơ số.
Lời giải
Ta có: 315 : 35 = 315 – 5 = 310.
Đáp án D.
Câu 6. Kết quả của phép tính 55.53 là:
A. 515 | B. 58 |
C. 2515 | D. 108 |
Phương pháp
Dựa vào quy tắc nhân hai lũy thừa cùng cơ số.
Lời giải
Ta có: 55.53 = 55 + 3 = 58.
Đáp án B.
Câu 7. Lũy thừa 72 có giá trị bằng
A.14 | B. 9 |
C. 49 | D. 32 |
Phương pháp
Dựa vào kiến thức lũy thừa.
Lời giải
Ta có: 72 = 7.7 = 49.
Đáp án C.
Câu 8. Số nào sau đây chia hết cho 2 và 3?
A.32 | B. 42 |
C. 52 | D. 62 |
Phương pháp
Dựa vào dấu hiệu chia hết cho 2, 3.
Lời giải
Số chia hết cho 2 có chữ số tận cùng là 0; 2; 4; 6; 8.
Số chia hết cho 3 có tổng các chữ số chia hết cho 3.
+) 3 + 2 = 5 nên 32 không chia hết cho 3.
+) 4 + 2 = 6 nên 42 chia hết cho 3.
+) 5 + 2 = 7 nên 52 không chia hết cho 3.
+) 6 + 2 = 8 nên 62 không chia hết cho 3.
Đáp án B.
Câu 9. Các số 2;17;37. Số nguyên tố là:
A. 2 | B. 17 |
C. 37 | D. cả 3 số trên |
Phương pháp
Sử dụng kiến thức về số nguyên tố.
Lời giải
Ta thấy 2, 17, 37 đều là các số nguyên tố nên ta chọn D.
Đáp án D.
Câu 10. Số 780 được phân tích ra thừa số nguyên tố là:
A. 780 = 4.3.5.13 | B. 780 = 22.15.13 |
C. 780 = 12.5.13 | D. 780 = 22.3.5.13 |
Phương pháp
Phân tích số 780 ra thành tích các thừa số nguyên tố.
Lời giải
780 = 2.2.3.5.13 = 22.3.5.13.
Đáp án D.
Câu 11. Xét tập hợp N, trong các số sau, bội của 16 là
A. 28 | B. 48 |
C. 36 | D. 8 |
Phương pháp
Dựa vào kiến thức về bội số.
Lời giải
Ta có: 48 = 16.3 nên 48 là bội của 3.
Đáp ánD.
Câu 12. Trong phép chia cho 3 số dư có thể là:
A. 1;2;3 | B. 0;1;2 |
C. 1;2 | D. 0;1 |
Phương pháp
Số dư phải nhỏ hơn số chia.
Lời giải
Số dư có thể trong phép chia cho 3 là 0; 1; 2.
Đáp án B.
Câu 13. Kết quả so sánh hai số 72 và 27 là?
A. 72 > 27 | B. 72 ≥ 27 |
C. 72 = 27 | D. 72 < 27 |
Phương pháp
Đưa 27 về lũy thừa cùng số mũ với 72 để so sánh.
Lời giải
Ta có: 27 = (23)2.2 = 82.2.
Vì 82 > 72 nên 82.2 > 72 hay 27 > 72.
Đáp án D.
Câu 14. Chữ số x, y được thay vào số \(\overline {35x98y} \) để số đó chia hết cho 2;5 và 9 là:
A. x = 2; y = 0 | B. x = 0; y = 2 |
C. x = 3, y = 8 | D. x = 9; y = 0 |
Phương pháp
Dựa vào dấu hiệu chia hết cho 2;5 và 9.
Lời giải
Số chia hết cho 2 và 5 có chữ số tận cùng là 0 nên y = 0.
Số chia hết cho 9 thì tổng các chữ số chia hết cho 9 hay 3 + 5 + x + 9 + 8 + 0 = 25 + x chia hết cho 9.
Mà x là chữ số nên x = 2 (khi đó số \(\overline {35x98y} \) có tổng các chữ số là 25 + 2 = 27 chia hết cho 9).
Đáp án A.
Câu 15. Hiệu 11.9.5.2 – 48 chia hết cho
A. 2 và 3 | B. 2 và 9 |
C. 3 và 5 | D. 2 và 5 |
Phương pháp
Dựa vào dấu hiệu chia hết cho 2; 3; 5 và 9.
Lời giải
Vì 48 ⋮ 2 và tích 11.9.5.2 ⋮ 2 ⇒ 11.9.5.2−48 ⋮ 2.
Vì 48 ⋮ 3 và tích 11.9.5.2 ⋮ 3 ⇒ 11.9.5.2−48 ⋮ 3.
Đáp án A.
Câu 16. Quan sát các hình sau, hình bình hành là hình:

A. Hình 1. | B. Hình 2. |
C. Hình 3. | D. Hình 4. |
Phương pháp
Dựa vào kiến thức về hình bình hành.
Lời giải
Hình bình hành là hình có các cặp cạnh đối bằng nhau nên Hình 3 là hình bình hành.
Đáp án C.
Câu 17. Cho tam giác đều ABC, biết AB = 3cm. Khi đó AC có độ dài là
A. 5cm | B. 4cm |
C. 3cm | D. 2cm |
Phương pháp
Dựa vào đặc điểm của tam giác đều.
Lời giải
Tam giác đều có 3 cạnh bằng nhau nên AB = BC = AC = 3cm.
Đáp án C.
Câu 18. Một mảnh vườn hình vuông có chiều dài cạnh là 24m. Khi đó chu vi mảnh vườn là:
A. 24m | B. 96m |
C. 576m | D. 48m |
Phương pháp
Dựa vào đặc điểm của hình vuông.
Lời giải
Chu vi của mảnh vườn là:
24.4 = 96(m).
Đáp án B.
Câu 19. Ghép 6 tam giác đều có độ dài cạnh là 5cm thành một lục giác đều. Khi đó độ dài đường chéo chính là:
A. 5cm. | B. 15cm. |
C. 10cm. | D. 30cm. |
Phương pháp
Dựa vào đặc điểm của hình tam giác đều và lục giác đều.
Lời giải
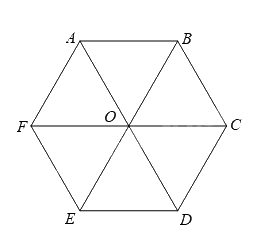
Hình lục giác đều ghép từ 6 tam giác đều thì độ dài đường chéo sẽ gấp 2 lần độ dài cạnh của tam giác đều.
=> Độ dài đường chéo chính là: 5.2 = 10.
Đáp án C.
Câu 20. Một miếng gỗ hình thoi có kích thước hai đường chéo lần lượt là 5cm; 8cm. Diện tích của miếng gỗ là:
A. 20cm2 | B. 26cm2 |
C. 40cm2 | D. 13cm2 |
Phương pháp
Sử dụng công thức tính diện tích hình thoi.
Lời giải
Diện tích hình thoi là: \(\frac{1}{2}\).5.8 = 20(cm2).
Đáp án A.
Phần tự luận.
Bài 1(1,75 điểm). Tính:
a) 23.5 – 23.3 | b) 125 - {2.[2.52 – (31 - 2.3)]} + 3.25 |
Phương pháp
Dựa vào quy tắc dấu ngoặc, quy tắc tính toán lũy thừa.
Lời giải
a) 23.5 – 23.3 = 23.(5-3) = 23.2 = 24 = 16 | b) 125 - {2.[2.52 – (31 -2.3)]} + 3.25 = 125 – {2.[2.25 – (31 - 6)]} + 75 = 125 - {2.[50 – 25]} + 75 = 125 – {2.25} + 75 = 125 – 50 + 75 = 75 + 75 = 150 |
Bài 2 (1 điểm): Tìm số tự nhiên x, biết: (x – 11) . 4 = 43 : 2
Phương pháp
Sử dụng quy tắc chuyển vế, quy tắc tính để tìm x.
Lời giải
(x – 11) . 4 = 43 : 2
(x – 11) . 4 = 32
x – 11 = 32 : 4
x – 11 = 8
x = 19
Vậy x = 19.
Bài 3 (1 điểm):Khối 6 của một trường THCS có 143 học sinh đi tham quan. Biết một xe có 16 chỗ ngồi. Hỏi cần ít nhất bao nhiêu xe để chở hết số học sinh đó.
Phương pháp
Thực hiện phép chia 143 với 16.
Lời giải
Ta có: 143:16 = 8( dư 15)
Khi xếp 143 học sinh vào mỗi xe 16 học sinh thì hết 8 xe và còn dư 15 học sinh. Nên cần thêm 1 xe nữa để chở số học sinh còn dư
Cần ít nhất số xe là:
8 + 1 = 9 ( xe)
Vậy để chở 143 học sinh bằng xe 16 chỗ ngồi thì cần ít nhất 9 xe.
Bài 4 (1,25 điểm): Một khu vườn hình chữ nhật có diện tích 4500 m2, chiều rộng 50m, cửa vào khu vườn rộng 5m. Người ta muốn làm hàng rào xung quanh vườn bằng hai tầng dây thép gai. Hỏi cần phải dùng bao nhiêu mét dây thép gai để làm hàng rào?
Phương pháp
Tính chiều dài khu vườn, chu vi khu vườn.
Độ dài cần phải làm hàng rào = chu vi khu vườn – cửa vào.
Tính độ dài dây thép gai = độ dài hàng rào . 2.
Lời giải
Chiều dài của khu vườn là:
4500: 50 = 90 (m)
Chu vi của khu vườn là:
2. (50 + 90) = 280(m)
Trừ cửa vào khu vườn nên độ dài cần phải làm hàng rào là:
280 – 5 = 275 (m)
Người ta muốn làm hàng rào xung quanh vườn bằng hai tầng dây thép gai nên số mét dây thép gai dùng để làm hàng rào là:
275. 2 = 550 (m)
Vậy cần dùng 550 m dây thép gai dùng để làm hàng rào.
Bài 5 (1 điểm): Cho B = 31 + 32 + 33 + ...+ 3300. Chứng minh rằng B chia hết cho 2
Phương pháp
Xác định số số hạng của B.
Nhóm 2 hạng tử liên tiếp thành một nhóm, đưa nhân tử chung ra ngoài.
Chứng minh B bằng tích của 2 và một số hạng khác nên B luôn chia hết cho 2.
Lời giải
B = 31 + 32 + 33 + ...+ 3300
Tập hợp B có 300 số hạng
Ta có 300\( \vdots \) 2
B = 31 + 32 + 33 + ….+ 3300
B = ( 31 + 32) + ( 33 + 34) + …. + ( 3299 + 3300)
B = 3.(1 + 3) + 32.(1 + 3) + …+ 3299.(1+ 3)
B = 3. 4 + 32.4 + … + 3299.4
B = 4.(3 + 32 + … + 3299)
Vì 4\( \vdots \) 2 nên B = 4.(3 + 32 + … + 3299) \( \vdots \) 2
Vậy B \( \vdots \) 2
Tải về
Phần trắc nghiệm (4 điểm)
Câu 1. Cho tập hợp M = {5;7;9;11}. Cách viết nào sau đây là đúng?
A. {5} \( \in \) M
B. 7\( \in \;\)M
C. 11 \( \notin \) M
D. \(\left\{ {9;11} \right\}\) \( \notin \) M
Câu 2. Cho các cách viết sau: A = { a, b, c, d}; B = {2; 13; 45}; C = (1; 2; 3); D = 1. Có bao nhiêu cách viết tập hợp là đúng trong các cách viết trên?
A. 1
B. 2
C. 3
D. 4
Câu 3. Các số La Mã XV, XXI được đọc lần lượt là:
A. mười lăm, hai mốt
B. mười năm, hai mốt
C. mười lăm, hai mươi mốt
D. mười bốn, mười chín
Câu 4. Tập hợp A các số tự nhiên có hai chữ số nhỏ hơn 15 là:
A. A = {10;11;12;13;14}
B. A = 11;12;13;14
C. A = {11;12;13;14}
D. A = {11;12;13;14;15}
Câu 5. Kết quả của phép tính 315 : 35 là:
A. 13
B. 320
C. 33
D. 310
Câu 6. Kết quả của phép tính 55.53 là:
A. 515
B. 58
C. 2515
D. 108
Câu 7. Lũy thừa 72 có giá trị bằng
A.14
B. 9
C. 49
D. 32
Câu 8. Số nào sau đây chia hết cho 2 và 3?
A.32
B. 42
C. 52
D. 62
Câu 9. Các số 2;17;37. Số nguyên tố là:
A. 2
B. 17
C. 37
D. cả 3 số trên
Câu 10. Số 780 được phân tích ra thừa số nguyên tố là:
A. 780 = 4.3.5.13
B. 780 = 22.15.13
C. 780 = 12.5.13
D. 780 = 22.3.5.13
Câu 11. Xét tập hợp N, trong các số sau, bội của 16 là
A. 28
B. 48
C. 36
D. 8
Câu 12. Trong phép chia cho 3 số dư có thể là:
A. 1;2;3
B. 0;1;2
C. 1;2
D. 0;1
Câu 13. Kết quả so sánh hai số 72 và 27 là?
A. 72 > 27
B. 72 ≥ 27
C. 72 = 27
D. 72 < 27
Câu 14. Chữ số x, y được thay vào số \(\overline {35x98y} \) để số đó chia hết cho 2;5 và 9 là:
A. x = 2; y = 0
B. x = 0; y = 2
C. x = 3, y = 8
D. x = 9; y = 0
Câu 15. Hiệu 11.9.5.2 – 48 chia hết cho
A. 2 và 3
B. 2 và 9
C. 3 và 5
D. 2 và 5
Câu 16. Quan sát các hình sau, hình bình hành là hình:

A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Câu 17. Cho tam giác đều ABC, biết AB = 3cm. Khi đó AC có độ dài là
A. 5cm
B. 4cm
C. 3cm
D. 2cm
Câu 18. Một mảnh vườn hình vuông có chiều dài cạnh là 24m. Khi đó chu vi mảnh vườn là:
A. 24m
B. 96m
C. 576m
D. 48m
Câu 19. Ghép 6 tam giác đều có độ dài cạnh là 5cm thành một lục giác đều. Khi đó độ dài đường chéo chính là:
A. 5cm.
B. 15cm.
C. 10cm.
D. 30cm.
Câu 20. Một miếng gỗ hình thoi có kích thước hai đường chéo lần lượt là 5cm; 8cm. Diện tích của miếng gỗ là:
A. 20cm2
B. 26cm2
C. 40cm2
D. 13cm2
Phần tự luận (6 điểm)
Bài 1(1,75 điểm): Tính:
a) 23.5 – 23.3
b) 125 - {2.[2.52 – (31 - 2.3)]} + 3.25
Bài 2 (1 điểm): Tìm số tự nhiên x, biết: (x – 11) . 4 = 43 : 2
Bài 3 (1 điểm):Khối 6 của một trường THCS có 143 học sinh đi tham quan. Biết một xe có 16 chỗ ngồi. Hỏi cần ít nhất bao nhiêu xe để chở hết số học sinh đó.
Bài 4 (1,25 điểm): Một khu vườn hình chữ nhật có diện tích 4500 m2, chiều rộng 50m, cửa vào khu vườn rộng 5m. Người ta muốn làm hàng rào xung quanh vườn bằng hai tầng dây thép gai. Hỏi cần phải dùng bao nhiêu mét dây thép gai để làm hàng rào?
Bài 5 (1 điểm): Cho B = 31 + 32 + 33 + ...+ 3300. Chứng minh rằng B chia hết cho 2
-------- Hết --------
Phần trắc nghiệm
Câu 1: B | Câu 2: A | Câu 3: C | Câu 4: A | Câu 5: D |
Câu 6: B | Câu 7: C | Câu 8: B | Câu 9: D | Câu 10: D |
Câu 11: B | Câu 12: B | Câu 13: D | Câu 14: A | Câu 15: A |
Câu 16: C | Câu 17: C | Câu 18: B | Câu 19: C | Câu 20: A |
Câu 1. Cho tập hợp M = {5;7;9;11}. Cách viết nào sau đây là đúng?
A. {5} \( \in \) M | B. 7\( \in \;\)M |
C. 11 \( \notin \) M | D. \(\left\{ {9;11} \right\}\) \( \notin \) M |
Phương pháp
Dựa vào cách viết tập hợp và phần tử.
Lời giải
{5}, \(\left\{ {9;11} \right\}\) là kí hiệu một tập hợp => không sử dụng dấu \( \in \) nên A và D sai.
7 \( \in \;\). M nên B đúng.
11 \( \in \). M nên C sai.
Đáp án B.
Câu 2. Cho các cách viết sau: A = {a, b, c, d}; B = {2; 13; 45}; C = (1; 2; 3); D = 1. Có bao nhiêu cách viết tập hợp là đúng trong các cách viết trên?
A. 1 | B. 2 |
C. 3 | D. 4 |
Phương pháp
Các phần tử của tập hợp được viết trong hai dấu ngoặc nhọn {}, cách nhau bởi dấu “;”.
Lời giải
Cách viết đúng là B = {2; 13; 45}
Vậy có 1 cách viết đúng.
Đáp án A.
Câu 3. Các số La Mã XV, XXI được đọc lần lượt là:
A. mười lăm, hai mốt | B. mười năm, hai mốt |
C. mười lăm, hai mươi mốt | D. mười bốn, mười chín |
Phương pháp
Dựa vào kiến thức về số La Mã.
Lời giải
Các số La Mã XV, XXI biểu diễn các số tự nhiên 15, 21 và được đọc lần lượt là: mười lăm, hai mươi mốt.
Đáp án C.
Câu 4. Tập hợp A các số tự nhiên có hai chữ số nhỏ hơn 15 là:
A. A = {10;11;12;13;14} | B. A = 11;12;13;14 |
C. A = {11;12;13;14} | D. A = {11;12;13;14;15} |
Phương pháp
Dựa vào cách mô ta một tập hợp.
Lời giải
Tập hợp các số tự nhiên có hai chữ số nhỏ hơn 15 là: A = {10;11;12;13;14}
Đáp án A.
Câu 5. Kết quả của phép tính 315 : 35 là:
A. 13 | B. 320 |
C. 33 | D. 310 |
Phương pháp
Dựa vào quy tắc chia lũy thừa cùng cơ số.
Lời giải
Ta có: 315 : 35 = 315 – 5 = 310.
Đáp án D.
Câu 6. Kết quả của phép tính 55.53 là:
A. 515 | B. 58 |
C. 2515 | D. 108 |
Phương pháp
Dựa vào quy tắc nhân hai lũy thừa cùng cơ số.
Lời giải
Ta có: 55.53 = 55 + 3 = 58.
Đáp án B.
Câu 7. Lũy thừa 72 có giá trị bằng
A.14 | B. 9 |
C. 49 | D. 32 |
Phương pháp
Dựa vào kiến thức lũy thừa.
Lời giải
Ta có: 72 = 7.7 = 49.
Đáp án C.
Câu 8. Số nào sau đây chia hết cho 2 và 3?
A.32 | B. 42 |
C. 52 | D. 62 |
Phương pháp
Dựa vào dấu hiệu chia hết cho 2, 3.
Lời giải
Số chia hết cho 2 có chữ số tận cùng là 0; 2; 4; 6; 8.
Số chia hết cho 3 có tổng các chữ số chia hết cho 3.
+) 3 + 2 = 5 nên 32 không chia hết cho 3.
+) 4 + 2 = 6 nên 42 chia hết cho 3.
+) 5 + 2 = 7 nên 52 không chia hết cho 3.
+) 6 + 2 = 8 nên 62 không chia hết cho 3.
Đáp án B.
Câu 9. Các số 2;17;37. Số nguyên tố là:
A. 2 | B. 17 |
C. 37 | D. cả 3 số trên |
Phương pháp
Sử dụng kiến thức về số nguyên tố.
Lời giải
Ta thấy 2, 17, 37 đều là các số nguyên tố nên ta chọn D.
Đáp án D.
Câu 10. Số 780 được phân tích ra thừa số nguyên tố là:
A. 780 = 4.3.5.13 | B. 780 = 22.15.13 |
C. 780 = 12.5.13 | D. 780 = 22.3.5.13 |
Phương pháp
Phân tích số 780 ra thành tích các thừa số nguyên tố.
Lời giải
780 = 2.2.3.5.13 = 22.3.5.13.
Đáp án D.
Câu 11. Xét tập hợp N, trong các số sau, bội của 16 là
A. 28 | B. 48 |
C. 36 | D. 8 |
Phương pháp
Dựa vào kiến thức về bội số.
Lời giải
Ta có: 48 = 16.3 nên 48 là bội của 3.
Đáp ánD.
Câu 12. Trong phép chia cho 3 số dư có thể là:
A. 1;2;3 | B. 0;1;2 |
C. 1;2 | D. 0;1 |
Phương pháp
Số dư phải nhỏ hơn số chia.
Lời giải
Số dư có thể trong phép chia cho 3 là 0; 1; 2.
Đáp án B.
Câu 13. Kết quả so sánh hai số 72 và 27 là?
A. 72 > 27 | B. 72 ≥ 27 |
C. 72 = 27 | D. 72 < 27 |
Phương pháp
Đưa 27 về lũy thừa cùng số mũ với 72 để so sánh.
Lời giải
Ta có: 27 = (23)2.2 = 82.2.
Vì 82 > 72 nên 82.2 > 72 hay 27 > 72.
Đáp án D.
Câu 14. Chữ số x, y được thay vào số \(\overline {35x98y} \) để số đó chia hết cho 2;5 và 9 là:
A. x = 2; y = 0 | B. x = 0; y = 2 |
C. x = 3, y = 8 | D. x = 9; y = 0 |
Phương pháp
Dựa vào dấu hiệu chia hết cho 2;5 và 9.
Lời giải
Số chia hết cho 2 và 5 có chữ số tận cùng là 0 nên y = 0.
Số chia hết cho 9 thì tổng các chữ số chia hết cho 9 hay 3 + 5 + x + 9 + 8 + 0 = 25 + x chia hết cho 9.
Mà x là chữ số nên x = 2 (khi đó số \(\overline {35x98y} \) có tổng các chữ số là 25 + 2 = 27 chia hết cho 9).
Đáp án A.
Câu 15. Hiệu 11.9.5.2 – 48 chia hết cho
A. 2 và 3 | B. 2 và 9 |
C. 3 và 5 | D. 2 và 5 |
Phương pháp
Dựa vào dấu hiệu chia hết cho 2; 3; 5 và 9.
Lời giải
Vì 48 ⋮ 2 và tích 11.9.5.2 ⋮ 2 ⇒ 11.9.5.2−48 ⋮ 2.
Vì 48 ⋮ 3 và tích 11.9.5.2 ⋮ 3 ⇒ 11.9.5.2−48 ⋮ 3.
Đáp án A.
Câu 16. Quan sát các hình sau, hình bình hành là hình:

A. Hình 1. | B. Hình 2. |
C. Hình 3. | D. Hình 4. |
Phương pháp
Dựa vào kiến thức về hình bình hành.
Lời giải
Hình bình hành là hình có các cặp cạnh đối bằng nhau nên Hình 3 là hình bình hành.
Đáp án C.
Câu 17. Cho tam giác đều ABC, biết AB = 3cm. Khi đó AC có độ dài là
A. 5cm | B. 4cm |
C. 3cm | D. 2cm |
Phương pháp
Dựa vào đặc điểm của tam giác đều.
Lời giải
Tam giác đều có 3 cạnh bằng nhau nên AB = BC = AC = 3cm.
Đáp án C.
Câu 18. Một mảnh vườn hình vuông có chiều dài cạnh là 24m. Khi đó chu vi mảnh vườn là:
A. 24m | B. 96m |
C. 576m | D. 48m |
Phương pháp
Dựa vào đặc điểm của hình vuông.
Lời giải
Chu vi của mảnh vườn là:
24.4 = 96(m).
Đáp án B.
Câu 19. Ghép 6 tam giác đều có độ dài cạnh là 5cm thành một lục giác đều. Khi đó độ dài đường chéo chính là:
A. 5cm. | B. 15cm. |
C. 10cm. | D. 30cm. |
Phương pháp
Dựa vào đặc điểm của hình tam giác đều và lục giác đều.
Lời giải
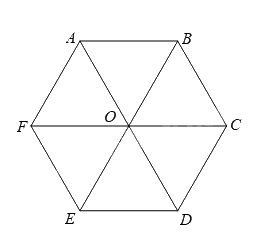
Hình lục giác đều ghép từ 6 tam giác đều thì độ dài đường chéo sẽ gấp 2 lần độ dài cạnh của tam giác đều.
=> Độ dài đường chéo chính là: 5.2 = 10.
Đáp án C.
Câu 20. Một miếng gỗ hình thoi có kích thước hai đường chéo lần lượt là 5cm; 8cm. Diện tích của miếng gỗ là:
A. 20cm2 | B. 26cm2 |
C. 40cm2 | D. 13cm2 |
Phương pháp
Sử dụng công thức tính diện tích hình thoi.
Lời giải
Diện tích hình thoi là: \(\frac{1}{2}\).5.8 = 20(cm2).
Đáp án A.
Phần tự luận.
Bài 1(1,75 điểm). Tính:
a) 23.5 – 23.3 | b) 125 - {2.[2.52 – (31 - 2.3)]} + 3.25 |
Phương pháp
Dựa vào quy tắc dấu ngoặc, quy tắc tính toán lũy thừa.
Lời giải
a) 23.5 – 23.3 = 23.(5-3) = 23.2 = 24 = 16 | b) 125 - {2.[2.52 – (31 -2.3)]} + 3.25 = 125 – {2.[2.25 – (31 - 6)]} + 75 = 125 - {2.[50 – 25]} + 75 = 125 – {2.25} + 75 = 125 – 50 + 75 = 75 + 75 = 150 |
Bài 2 (1 điểm): Tìm số tự nhiên x, biết: (x – 11) . 4 = 43 : 2
Phương pháp
Sử dụng quy tắc chuyển vế, quy tắc tính để tìm x.
Lời giải
(x – 11) . 4 = 43 : 2
(x – 11) . 4 = 32
x – 11 = 32 : 4
x – 11 = 8
x = 19
Vậy x = 19.
Bài 3 (1 điểm):Khối 6 của một trường THCS có 143 học sinh đi tham quan. Biết một xe có 16 chỗ ngồi. Hỏi cần ít nhất bao nhiêu xe để chở hết số học sinh đó.
Phương pháp
Thực hiện phép chia 143 với 16.
Lời giải
Ta có: 143:16 = 8( dư 15)
Khi xếp 143 học sinh vào mỗi xe 16 học sinh thì hết 8 xe và còn dư 15 học sinh. Nên cần thêm 1 xe nữa để chở số học sinh còn dư
Cần ít nhất số xe là:
8 + 1 = 9 ( xe)
Vậy để chở 143 học sinh bằng xe 16 chỗ ngồi thì cần ít nhất 9 xe.
Bài 4 (1,25 điểm): Một khu vườn hình chữ nhật có diện tích 4500 m2, chiều rộng 50m, cửa vào khu vườn rộng 5m. Người ta muốn làm hàng rào xung quanh vườn bằng hai tầng dây thép gai. Hỏi cần phải dùng bao nhiêu mét dây thép gai để làm hàng rào?
Phương pháp
Tính chiều dài khu vườn, chu vi khu vườn.
Độ dài cần phải làm hàng rào = chu vi khu vườn – cửa vào.
Tính độ dài dây thép gai = độ dài hàng rào . 2.
Lời giải
Chiều dài của khu vườn là:
4500: 50 = 90 (m)
Chu vi của khu vườn là:
2. (50 + 90) = 280(m)
Trừ cửa vào khu vườn nên độ dài cần phải làm hàng rào là:
280 – 5 = 275 (m)
Người ta muốn làm hàng rào xung quanh vườn bằng hai tầng dây thép gai nên số mét dây thép gai dùng để làm hàng rào là:
275. 2 = 550 (m)
Vậy cần dùng 550 m dây thép gai dùng để làm hàng rào.
Bài 5 (1 điểm): Cho B = 31 + 32 + 33 + ...+ 3300. Chứng minh rằng B chia hết cho 2
Phương pháp
Xác định số số hạng của B.
Nhóm 2 hạng tử liên tiếp thành một nhóm, đưa nhân tử chung ra ngoài.
Chứng minh B bằng tích của 2 và một số hạng khác nên B luôn chia hết cho 2.
Lời giải
B = 31 + 32 + 33 + ...+ 3300
Tập hợp B có 300 số hạng
Ta có 300\( \vdots \) 2
B = 31 + 32 + 33 + ….+ 3300
B = ( 31 + 32) + ( 33 + 34) + …. + ( 3299 + 3300)
B = 3.(1 + 3) + 32.(1 + 3) + …+ 3299.(1+ 3)
B = 3. 4 + 32.4 + … + 3299.4
B = 4.(3 + 32 + … + 3299)
Vì 4\( \vdots \) 2 nên B = 4.(3 + 32 + … + 3299) \( \vdots \) 2
Vậy B \( \vdots \) 2
Đề thi giữa kì 1 Toán 6 - Đề số 8 là một công cụ đánh giá quan trọng giúp học sinh lớp 6 kiểm tra mức độ nắm vững kiến thức đã học trong giai đoạn đầu năm học. Đề thi này thường bao gồm các chủ đề chính như số tự nhiên, phép tính với số tự nhiên, ước và bội, tập hợp, và các bài toán thực tế liên quan.
Cấu trúc của đề thi có thể khác nhau tùy theo từng trường và giáo viên, nhưng nhìn chung, đề thi thường bao gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 1 Toán 6 - Đề số 8:
Các bài tập về số tự nhiên thường tập trung vào:
Các bài tập về phép tính với số tự nhiên bao gồm:
Các bài tập về ước và bội thường yêu cầu học sinh:
Các bài tập về tập hợp thường liên quan đến:
Ví dụ 1: Tính 123 + 456 - 789
Giải:
Ví dụ 2: Tìm tất cả các ước của 12
Giải:
Các ước của 12 là: 1, 2, 3, 4, 6, 12
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi giữa kì 1 Toán 6!