Chào mừng các em học sinh lớp 6 đến với đề thi học kì 1 Toán 6 - Đề số 3 của giaitoan.edu.vn. Đề thi này được biên soạn dựa trên chương trình học Toán 6, bao gồm các dạng bài tập thường gặp trong đề thi chính thức.
Mục tiêu của đề thi này là giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự đánh giá năng lực của bản thân trước khi bước vào kỳ thi quan trọng.
Phần I: Trắc nghiệm (4 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (4 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Phần tử nào không thuộc tập hợp \(A = \left\{ {\left. {x \in \mathbb{N}} \right|10 \le x < 20} \right\}\)
A. \(20\)
B. \(10\)
C. \(19\)
D. \(15\)
Câu 2. Bội chung nhỏ nhất của \(12;15;18\) là:
A. \(360\)
B. \(180\)
C. \(450\)
D. \(90\)
Câu 3. Lũy thừa với số mũ là \(5\) cơ số là \(12\) được viết là:
A. \({12^5}\)
B. \({5^{12}}\)
C. \({51^2}\)
D. \({21^5}\)
Câu 4. Số nào chia hết cho \(5\) nhưng không chia hết cho \(9\)?
A. \(180\)
B. \(225\)
C. \(405\)
D. \(305\)
Câu 5. Chiếc diều của bạn Minh bay cao \(15m\) (so với mặt đất). Sau một lúc, độ cao của chiếc diều tăng \(2m\), rồi sau đó lại giảm \(3m\). Hỏi chiếc diều ở độ cao bao nhiêu (so với mặt đất) sau hai lần thay đổi?
A. \(13m\)
B. \(14m\)
C.\(16m\)
D. \(21m\)
Câu 6. Tập hợp chỉ gồm các số nguyên tố?
A. \(\left\{ {1\,;\,2\,;\,5\,;\,7} \right\}\)
B. \(\left\{ {3\,;\,10\,;\,7\,;\,13} \right\}\)
C. \(\left\{ {3\,;\,5\,;\,7\,;\,11} \right\}\)
D. \(\left\{ {13\,;\,15\,;\,17\,;\,19} \right\}\)
Câu 7. Trong các số nguyên sau: \(\left( { - 2022} \right)\,;\,\left( { - 2000} \right)\,;\,\left( { - 2021} \right)\,;\,\left( { - 1999} \right)\). Số lớn nhất là:
A. \( - 1999\)
B. \( - 2022\)
C. \( - 2000\)
D. \( - 2021\)
Câu 8. Trong các hình dưới đây, hình nào có tâm đối xứng?
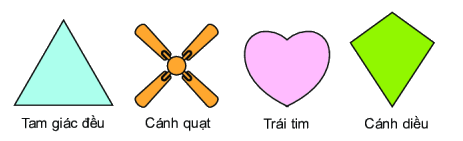
A. Tam giác đều
B. Cánh quạt
C. Trái tim
D. Cánh diều
Câu 9. Một khu vườn thoi có độ dài hai đường chéo lần lượt là \(8m\) và \(6m\). Khi đó, diện tích khu vườn là:
A. \(24{m^2}\)
B. \(12{m^2}\)
C. \(48{m^2}\)
D. \(36{m^2}\)
Câu 10. Một thửa ruộng hình bình hành có cạnh \(30m\) chiều cao tương ứng \(12m.\) Người ta trồng lúa trên mảnh ruộng, năng suất lúa là \(0,8\,kg/{m^2}.\) Tính sản lượng lúa thu hoạch được của thửa ruộng đó.
A. \(228\,kg\)
B. \(288\,kg\)
C. \(360\,kg\)
D. \(144\,kg\)
Phần II. Tự luận (6 điểm):
Bài 1. (1,0 điểm) Thực hiện phép tính:
a) \(35 - \left\{ {12 - \left[ {\left( { - 14} \right) + \left( { - 2} \right)} \right]} \right\}\)
b) \(1997 - \left[ {10.\left( {{4^3} - 56} \right):{2^3} + {2^3}} \right]{.2023^0}\)
Bài 2. (1,0 điểm) Tìm \(x\), biết:
a) \(124 + \left( {118 - x} \right) = 217\)
b) \({3^{x + 2}} + {3^x} = 10\)
Bài 3. (1,5 điểm) Trong cuộc thi HSG cấp tỉnh có ba môn Toán, Văn, Anh; số học sinh tham gia như sau: Văn có 96 học sinh, Toán có 120 học sinh và Anh có 72 học sinh. Trong buổi tổng kết các bạn được tham gia phân công đứng thành hàng dọc sao cho mỗi hàng có số bạn thi mỗi môn bằng nhau. Hỏi có thể phân học sinh đứng thành ít nhất bao nhiêu hàng?
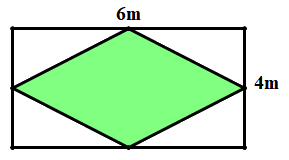
Bài 4. (2 điểm) Trong mảnh vườn hình chữ nhật có chiều dài \(6m\), chiều dài \(8m\), người ta trồng hoa hồng trong mảnh đất hình thoi như hình bên (mỗi đỉnh của hình thoi nằm chính giữa các cạnh của hình chữ nhật). Nếu mỗi mét vuông trồng được \(3\) cây hoa thì cần bao nhiêu cây để trồng mảnh đất hình thoi đó?
Bài 5. (0,5 điểm) Cho \(B = 3 + {3^2} + {3^3} + ... + {3^{2014}} + {3^{2015}}\). Chứng minh rằng \(2B + 3\) là một lũy thừa của \(3\).
Phần I: Trắc nghiệm
1. A | 2. B | 3. A | 4. D | 5. B | 6. C | 7. A | 8. B | 9. A | 10. B |
Câu 1
Phương pháp:
Liệt kê các phần tử của một tập hợp, sau đó kiểm tra xem phần tử có thuộc tập hợp hay không.
Cách giải:
Ta có: \(A = \left\{ {10;11;12;13;14;15;16;17;18;19} \right\}\).
Khi đó, nhận thấy \(20 \notin A\)
Chọn A.
Câu 2
Phương pháp:
Tìm bội chung nhỏ nhất của ba số tự nhiên bằng cách phân tích các số thành tích các số nguyên tố.
Cách giải:
Ta có: \(12 = {2^2}.3;15 = 3.5;18 = {2.3^2} \Rightarrow \)BCNN\(\left( {12,15,18} \right) = {2^2}{.3^2}.5 = 4.9.5 = 180\).
Chọn B.
Câu 3
Phương pháp:
Sử dụng định nghĩa lũy thừa với số mũ tự nhiên.
Cách giải:
Lũy thừa với số mũ là \(5\) cơ số là \(12\) được viết là: \({12^5}\)
Chọn A.
Câu 4
Phương pháp:
Sử dụng dấu hiệu chia hết cho \(5\) và \(9\).
Cách giải:
Ta có:
Số \(180\) có chữ số tận cùng là \(0\) nên chia hết cho \(5\) và \(1 + 8 + 0 = 9 \vdots 9 \Rightarrow 180 \vdots 9\).
Số \(225\) có chữ số tận cùng là \(5\) nên chia hết cho \(5\) và \(2 + 2 + 5 = 9 \vdots 9 \Rightarrow 225 \vdots 9\).
Số \(405\) có chữ số tận cùng là \(5\) nên chia hết cho \(5\) và \(4 + 0 + 5 = 9 \vdots 9 \Rightarrow 405 \vdots 9\).
Số \(305\) có chữ số tận cùng là \(5\) nên chia hết cho \(5\). Nhưng \(3 + 0 + 5 = 8\not{ \vdots }9 \Rightarrow 305\not{ \vdots }9\).
Chọn D.
Câu 5
Phương pháp:
Căn cứ vào yêu cầu đề bài, phân tích và đưa bài toán về thực hiện phép cộng với các số nguyên cho trước.
Cách giải:
Sau hai lần thay đổi, chiếc diều ở độ cao:
\(15 + 2 + \left( { - 3} \right) = 14\left( m \right)\)
Chọn B.
Câu 6
Phương pháp:
Vận dụng định nghĩa số nguyên tố .
Chú ý: số \(0\) và số \(1\) không là số nguyên tố; số \(2\) là số nguyên tố chẵn duy nhất.
Cách giải:
Ta có:
+ \(0\) không là số nguyên tố nên loại đáp án A
+ \(10\) là hợp số nên loại đáp án B
+ tất cả các phần tử đều là số nguyên tố nên chọn đáp án C
+ \(15\) là hợp số nên loại đáp án D.
Chọn C.
Câu 7
Phương pháp:
Vận dụng các bước làm so sánh hai số nguyên âm, ta làm như sau:
+ Bước 1: Bỏ dấu “\( - \)” trước hai số nguyên âm
+ Bước 2: Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu “\( - \)”) sẽ lớn hơn.
Cách giải:
Vì nên \( - 1999 > - 2000 > - 2021 > - 2022\)
Vậy \( - 1999\) là số nguyên âm lớn nhất\(1999 < 2000 < 2021 < 2022\)
Chọn A.
Câu 8
Phương pháp:
Sử dụng định nghĩa tâm đối xứng
Cách giải:
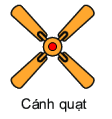
Nhận thấy chỉ có hình cánh quạt có tâm đối xứng.
Chọn B.
Câu 9
Phương pháp:
Sử dụng công thức tính diện tích hình thoi có độ dài hai đường chéo là \(m,n\) thì \(S = \dfrac{1}{2}m.n\)
Cách giải:
Diện tích của khu vườn là: \(\dfrac{1}{2}.8.6 = 24\left( {{m^2}} \right)\)
Chọn A.
Câu 10
Phương pháp:
Vận dụng công thức tính diện tích hình bình hành có hai cạnh là \(a,b\), có chiều cao tương ứng của cạnh \(a\) là \(h\) khi đó \(S = a.h\)
Sản lượng lúa thu được = diện tích của thửa ruộng \( \times \) năng suất của \(1\,{m^2}\)
Cách giải:
Diện tích của thửa ruộng là: \(12.30 = 360\left( {{m^2}} \right)\)
Sản lượng lúa thu hoạch được của thửa ruộng là: \(360.0,8 = 288\left( {kg} \right)\)
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp:
Biểu thức có ngoặc thực hiện theo thứ tự \(\left( {\,\,\,} \right) \to \left[ {\,\,\,} \right] \to \left\{ {\,\,\,} \right\}\)
Vận dụng quy tắc bỏ ngoặc có dấu “\( - \)” ở trước.
Thực hiện các phép toán với số nguyên.
Vận dụng kiến thức lũy thừa của một số tự nhiên.
Cách giải:
a) \(35 - \left\{ {12 - \left[ {\left( { - 14} \right) + \left( { - 2} \right)} \right]} \right\}\)
\(\begin{array}{l} = 35 - \left[ {12 - \left( { - 16} \right)} \right]\\ = 35 - \left( {12 + 16} \right)\\ = 35 - 28\\ = 7\end{array}\)
b) \(1997 - \left[ {10.\left( {{4^3} - 56} \right):{2^3} + {2^3}} \right]{.2023^0}\)
\(\begin{array}{l} = 1997 - \left[ {10.\left( {64 - 56} \right):8 + 8} \right].1\\ = 1997 - \left( {10.8:8 + 8} \right)\\ = 1997 - \left( {80:8 + 8} \right)\\ = 1997 - \left( {10 + 8} \right)\\ = 1997 - 18\\ = 1979\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số tự nhiên.
b) Vận dụng kiến thức lũy thừa với số mũ tự nhiên
Hai lũy thừa cùng cơ số bằng nhau khi số mũ của chúng bằng nhau.
Cách giải:
a) \(124 + \left( {118 - x} \right) = 217\)
\(\begin{array}{l}118 - x = 217 - 124\\118 - x = 93\\x = 118 - 93\\x = 25\end{array}\)
Vậy \(x = 25\)
b) \({3^{x + 2}} + {3^x} = 10\)
\(\begin{array}{l}{3^x}{.3^2} + {3^x} = 10\\{3^x}.\left( {{3^2} + 1} \right) = 10\\{3^x}.10 = 10\\{3^x} = 1\\{3^x} = {3^0}\\x = 0\end{array}\)
Vậy \(x = 0\)
Bài 3
Phương pháp:
Gọi số học sinh mỗi hàng là \(x\,\,\left( {x \in {\mathbb{N}^*}} \right)\) (học sinh)
Từ đề bài, suy ra \(x = \)ƯCLN\(\left( {96,120,72} \right)\)
Thực hiện phân tích các số \(96;\,120;72\) ra thừa số nguyên tố, từ đó tìm được ƯCLN\(\left( {96,\,120,72} \right)\)
Kết luận số học sinh ở mỗi hàng nhiều nhất.
Cách giải:
Gọi số học sinh mỗi hàng là \(x\,\,\left( {x \in {\mathbb{N}^*}} \right)\) (học sinh)
Theo đề bài, ta có: \(96\,\, \vdots \,\,x\,\,;\,\,\,120\,\, \vdots \,\,x\) và \(72\,\, \vdots \,\,x\,\,\,\,\left( 1 \right)\)
Để số hàng là ít nhất \( \Rightarrow \) Số học sinh mỗi hàng là nhiều nhất
\( \Rightarrow x\) lớn nhất (2)
Từ \(\left( 1 \right),\left( 2 \right) \Rightarrow x = \)ƯCLN\(\left( {96,120,72} \right)\)
Ta có: \(\left\{ \begin{array}{l}96 = {2^5}.3\\120 = {2^3}.3.5\\72 = {2^3}{.3^2}\end{array} \right.\,\, \Rightarrow \)ƯCLN\(\left( {96,120,72} \right) = {2^3}.3 = 24 \Rightarrow x = 24\)
\( \Rightarrow \) Số học sinh ở mỗi hàng nhiều nhất là \(24\).
Vậy số hàng ít nhất là: \(\left( {96 + 120 + 72} \right):24 = 12\) (hàng).
Bài 4
Phương pháp:
Sử dụng công thức tính diện tích hình thoi có độ dài hai đường chéo là \(m,n\) thì \(S = \dfrac{1}{2}m.n\)
Cách giải:
Diện tích của hình thoi là: \(\dfrac{1}{2}.6.4 = 12\left( {{m^2}} \right)\)
Số cây hoa để trồng trên mảnh đất hình thoi là: \(12.3 = 36\) (cây)
Bài 5
Phương pháp:
Sử dụng công thức nhân hai lũy thừa cùng cơ số.
Trừ các số hạng tương ứng từ hai vế của các đẳng thức.
Cách giải:
Ta có \(B = 3 + {3^2} + {3^3} + .... + {3^{2014}} + {3^{2015}}\) (1)
Nhân \(3\) vào hai vế của \(B\) ta được:
\(3B = 3\left( {3 + {3^2} + {3^3} + .... + {3^{2014}} + {3^{2015}}} \right) = 3.3 + {3.3^2} + {3.3^3} + ... + {3.3^{2014}} + {3.3^{2015}} = {3^2} + {3^3} + ... + {3^{2015}} + {3^{2016}}\) (2)
Lấy hai vế của (2) trừ hai vế tương ứng của (1) ta được:
\(\begin{array}{l}3B - B = \left( {{3^2} - {3^2}} \right) + \left( {{3^3} - {3^3}} \right) + .... + \left( {{3^{2014}} - {3^{2014}}} \right) + \left( {{3^{2015}} - {3^{2015}}} \right) + {3^{2016}} - 3\\2B = 0 + 0 + .... + {3^{2016}} - 3\\2B = {3^{2016}} - 3\end{array}\)
Suy ra \(2B + 3 = {3^{2016}}\)
Vậy \(2B + 3\) là một lũy thừa của \(3\).
Phần I: Trắc nghiệm (4 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Phần tử nào không thuộc tập hợp \(A = \left\{ {\left. {x \in \mathbb{N}} \right|10 \le x < 20} \right\}\)
A. \(20\)
B. \(10\)
C. \(19\)
D. \(15\)
Câu 2. Bội chung nhỏ nhất của \(12;15;18\) là:
A. \(360\)
B. \(180\)
C. \(450\)
D. \(90\)
Câu 3. Lũy thừa với số mũ là \(5\) cơ số là \(12\) được viết là:
A. \({12^5}\)
B. \({5^{12}}\)
C. \({51^2}\)
D. \({21^5}\)
Câu 4. Số nào chia hết cho \(5\) nhưng không chia hết cho \(9\)?
A. \(180\)
B. \(225\)
C. \(405\)
D. \(305\)
Câu 5. Chiếc diều của bạn Minh bay cao \(15m\) (so với mặt đất). Sau một lúc, độ cao của chiếc diều tăng \(2m\), rồi sau đó lại giảm \(3m\). Hỏi chiếc diều ở độ cao bao nhiêu (so với mặt đất) sau hai lần thay đổi?
A. \(13m\)
B. \(14m\)
C.\(16m\)
D. \(21m\)
Câu 6. Tập hợp chỉ gồm các số nguyên tố?
A. \(\left\{ {1\,;\,2\,;\,5\,;\,7} \right\}\)
B. \(\left\{ {3\,;\,10\,;\,7\,;\,13} \right\}\)
C. \(\left\{ {3\,;\,5\,;\,7\,;\,11} \right\}\)
D. \(\left\{ {13\,;\,15\,;\,17\,;\,19} \right\}\)
Câu 7. Trong các số nguyên sau: \(\left( { - 2022} \right)\,;\,\left( { - 2000} \right)\,;\,\left( { - 2021} \right)\,;\,\left( { - 1999} \right)\). Số lớn nhất là:
A. \( - 1999\)
B. \( - 2022\)
C. \( - 2000\)
D. \( - 2021\)
Câu 8. Trong các hình dưới đây, hình nào có tâm đối xứng?
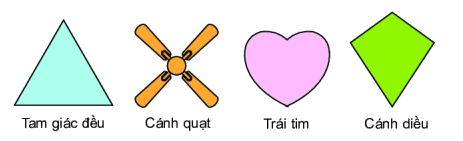
A. Tam giác đều
B. Cánh quạt
C. Trái tim
D. Cánh diều
Câu 9. Một khu vườn thoi có độ dài hai đường chéo lần lượt là \(8m\) và \(6m\). Khi đó, diện tích khu vườn là:
A. \(24{m^2}\)
B. \(12{m^2}\)
C. \(48{m^2}\)
D. \(36{m^2}\)
Câu 10. Một thửa ruộng hình bình hành có cạnh \(30m\) chiều cao tương ứng \(12m.\) Người ta trồng lúa trên mảnh ruộng, năng suất lúa là \(0,8\,kg/{m^2}.\) Tính sản lượng lúa thu hoạch được của thửa ruộng đó.
A. \(228\,kg\)
B. \(288\,kg\)
C. \(360\,kg\)
D. \(144\,kg\)
Phần II. Tự luận (6 điểm):
Bài 1. (1,0 điểm) Thực hiện phép tính:
a) \(35 - \left\{ {12 - \left[ {\left( { - 14} \right) + \left( { - 2} \right)} \right]} \right\}\)
b) \(1997 - \left[ {10.\left( {{4^3} - 56} \right):{2^3} + {2^3}} \right]{.2023^0}\)
Bài 2. (1,0 điểm) Tìm \(x\), biết:
a) \(124 + \left( {118 - x} \right) = 217\)
b) \({3^{x + 2}} + {3^x} = 10\)
Bài 3. (1,5 điểm) Trong cuộc thi HSG cấp tỉnh có ba môn Toán, Văn, Anh; số học sinh tham gia như sau: Văn có 96 học sinh, Toán có 120 học sinh và Anh có 72 học sinh. Trong buổi tổng kết các bạn được tham gia phân công đứng thành hàng dọc sao cho mỗi hàng có số bạn thi mỗi môn bằng nhau. Hỏi có thể phân học sinh đứng thành ít nhất bao nhiêu hàng?
Bài 4. (2 điểm) Trong mảnh vườn hình chữ nhật có chiều dài \(6m\), chiều dài \(8m\), người ta trồng hoa hồng trong mảnh đất hình thoi như hình bên (mỗi đỉnh của hình thoi nằm chính giữa các cạnh của hình chữ nhật). Nếu mỗi mét vuông trồng được \(3\) cây hoa thì cần bao nhiêu cây để trồng mảnh đất hình thoi đó?

Bài 5. (0,5 điểm) Cho \(B = 3 + {3^2} + {3^3} + ... + {3^{2014}} + {3^{2015}}\). Chứng minh rằng \(2B + 3\) là một lũy thừa của \(3\).
Phần I: Trắc nghiệm
1. A | 2. B | 3. A | 4. D | 5. B | 6. C | 7. A | 8. B | 9. A | 10. B |
Câu 1
Phương pháp:
Liệt kê các phần tử của một tập hợp, sau đó kiểm tra xem phần tử có thuộc tập hợp hay không.
Cách giải:
Ta có: \(A = \left\{ {10;11;12;13;14;15;16;17;18;19} \right\}\).
Khi đó, nhận thấy \(20 \notin A\)
Chọn A.
Câu 2
Phương pháp:
Tìm bội chung nhỏ nhất của ba số tự nhiên bằng cách phân tích các số thành tích các số nguyên tố.
Cách giải:
Ta có: \(12 = {2^2}.3;15 = 3.5;18 = {2.3^2} \Rightarrow \)BCNN\(\left( {12,15,18} \right) = {2^2}{.3^2}.5 = 4.9.5 = 180\).
Chọn B.
Câu 3
Phương pháp:
Sử dụng định nghĩa lũy thừa với số mũ tự nhiên.
Cách giải:
Lũy thừa với số mũ là \(5\) cơ số là \(12\) được viết là: \({12^5}\)
Chọn A.
Câu 4
Phương pháp:
Sử dụng dấu hiệu chia hết cho \(5\) và \(9\).
Cách giải:
Ta có:
Số \(180\) có chữ số tận cùng là \(0\) nên chia hết cho \(5\) và \(1 + 8 + 0 = 9 \vdots 9 \Rightarrow 180 \vdots 9\).
Số \(225\) có chữ số tận cùng là \(5\) nên chia hết cho \(5\) và \(2 + 2 + 5 = 9 \vdots 9 \Rightarrow 225 \vdots 9\).
Số \(405\) có chữ số tận cùng là \(5\) nên chia hết cho \(5\) và \(4 + 0 + 5 = 9 \vdots 9 \Rightarrow 405 \vdots 9\).
Số \(305\) có chữ số tận cùng là \(5\) nên chia hết cho \(5\). Nhưng \(3 + 0 + 5 = 8\not{ \vdots }9 \Rightarrow 305\not{ \vdots }9\).
Chọn D.
Câu 5
Phương pháp:
Căn cứ vào yêu cầu đề bài, phân tích và đưa bài toán về thực hiện phép cộng với các số nguyên cho trước.
Cách giải:
Sau hai lần thay đổi, chiếc diều ở độ cao:
\(15 + 2 + \left( { - 3} \right) = 14\left( m \right)\)
Chọn B.
Câu 6
Phương pháp:
Vận dụng định nghĩa số nguyên tố .
Chú ý: số \(0\) và số \(1\) không là số nguyên tố; số \(2\) là số nguyên tố chẵn duy nhất.
Cách giải:
Ta có:
+ \(0\) không là số nguyên tố nên loại đáp án A
+ \(10\) là hợp số nên loại đáp án B
+ tất cả các phần tử đều là số nguyên tố nên chọn đáp án C
+ \(15\) là hợp số nên loại đáp án D.
Chọn C.
Câu 7
Phương pháp:
Vận dụng các bước làm so sánh hai số nguyên âm, ta làm như sau:
+ Bước 1: Bỏ dấu “\( - \)” trước hai số nguyên âm
+ Bước 2: Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu “\( - \)”) sẽ lớn hơn.
Cách giải:
Vì nên \( - 1999 > - 2000 > - 2021 > - 2022\)
Vậy \( - 1999\) là số nguyên âm lớn nhất\(1999 < 2000 < 2021 < 2022\)
Chọn A.
Câu 8
Phương pháp:
Sử dụng định nghĩa tâm đối xứng
Cách giải:

Nhận thấy chỉ có hình cánh quạt có tâm đối xứng.
Chọn B.
Câu 9
Phương pháp:
Sử dụng công thức tính diện tích hình thoi có độ dài hai đường chéo là \(m,n\) thì \(S = \dfrac{1}{2}m.n\)
Cách giải:
Diện tích của khu vườn là: \(\dfrac{1}{2}.8.6 = 24\left( {{m^2}} \right)\)
Chọn A.
Câu 10
Phương pháp:
Vận dụng công thức tính diện tích hình bình hành có hai cạnh là \(a,b\), có chiều cao tương ứng của cạnh \(a\) là \(h\) khi đó \(S = a.h\)
Sản lượng lúa thu được = diện tích của thửa ruộng \( \times \) năng suất của \(1\,{m^2}\)
Cách giải:
Diện tích của thửa ruộng là: \(12.30 = 360\left( {{m^2}} \right)\)
Sản lượng lúa thu hoạch được của thửa ruộng là: \(360.0,8 = 288\left( {kg} \right)\)
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp:
Biểu thức có ngoặc thực hiện theo thứ tự \(\left( {\,\,\,} \right) \to \left[ {\,\,\,} \right] \to \left\{ {\,\,\,} \right\}\)
Vận dụng quy tắc bỏ ngoặc có dấu “\( - \)” ở trước.
Thực hiện các phép toán với số nguyên.
Vận dụng kiến thức lũy thừa của một số tự nhiên.
Cách giải:
a) \(35 - \left\{ {12 - \left[ {\left( { - 14} \right) + \left( { - 2} \right)} \right]} \right\}\)
\(\begin{array}{l} = 35 - \left[ {12 - \left( { - 16} \right)} \right]\\ = 35 - \left( {12 + 16} \right)\\ = 35 - 28\\ = 7\end{array}\)
b) \(1997 - \left[ {10.\left( {{4^3} - 56} \right):{2^3} + {2^3}} \right]{.2023^0}\)
\(\begin{array}{l} = 1997 - \left[ {10.\left( {64 - 56} \right):8 + 8} \right].1\\ = 1997 - \left( {10.8:8 + 8} \right)\\ = 1997 - \left( {80:8 + 8} \right)\\ = 1997 - \left( {10 + 8} \right)\\ = 1997 - 18\\ = 1979\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số tự nhiên.
b) Vận dụng kiến thức lũy thừa với số mũ tự nhiên
Hai lũy thừa cùng cơ số bằng nhau khi số mũ của chúng bằng nhau.
Cách giải:
a) \(124 + \left( {118 - x} \right) = 217\)
\(\begin{array}{l}118 - x = 217 - 124\\118 - x = 93\\x = 118 - 93\\x = 25\end{array}\)
Vậy \(x = 25\)
b) \({3^{x + 2}} + {3^x} = 10\)
\(\begin{array}{l}{3^x}{.3^2} + {3^x} = 10\\{3^x}.\left( {{3^2} + 1} \right) = 10\\{3^x}.10 = 10\\{3^x} = 1\\{3^x} = {3^0}\\x = 0\end{array}\)
Vậy \(x = 0\)
Bài 3
Phương pháp:
Gọi số học sinh mỗi hàng là \(x\,\,\left( {x \in {\mathbb{N}^*}} \right)\) (học sinh)
Từ đề bài, suy ra \(x = \)ƯCLN\(\left( {96,120,72} \right)\)
Thực hiện phân tích các số \(96;\,120;72\) ra thừa số nguyên tố, từ đó tìm được ƯCLN\(\left( {96,\,120,72} \right)\)
Kết luận số học sinh ở mỗi hàng nhiều nhất.
Cách giải:
Gọi số học sinh mỗi hàng là \(x\,\,\left( {x \in {\mathbb{N}^*}} \right)\) (học sinh)
Theo đề bài, ta có: \(96\,\, \vdots \,\,x\,\,;\,\,\,120\,\, \vdots \,\,x\) và \(72\,\, \vdots \,\,x\,\,\,\,\left( 1 \right)\)
Để số hàng là ít nhất \( \Rightarrow \) Số học sinh mỗi hàng là nhiều nhất
\( \Rightarrow x\) lớn nhất (2)
Từ \(\left( 1 \right),\left( 2 \right) \Rightarrow x = \)ƯCLN\(\left( {96,120,72} \right)\)
Ta có: \(\left\{ \begin{array}{l}96 = {2^5}.3\\120 = {2^3}.3.5\\72 = {2^3}{.3^2}\end{array} \right.\,\, \Rightarrow \)ƯCLN\(\left( {96,120,72} \right) = {2^3}.3 = 24 \Rightarrow x = 24\)
\( \Rightarrow \) Số học sinh ở mỗi hàng nhiều nhất là \(24\).
Vậy số hàng ít nhất là: \(\left( {96 + 120 + 72} \right):24 = 12\) (hàng).
Bài 4
Phương pháp:
Sử dụng công thức tính diện tích hình thoi có độ dài hai đường chéo là \(m,n\) thì \(S = \dfrac{1}{2}m.n\)
Cách giải:
Diện tích của hình thoi là: \(\dfrac{1}{2}.6.4 = 12\left( {{m^2}} \right)\)
Số cây hoa để trồng trên mảnh đất hình thoi là: \(12.3 = 36\) (cây)
Bài 5
Phương pháp:
Sử dụng công thức nhân hai lũy thừa cùng cơ số.
Trừ các số hạng tương ứng từ hai vế của các đẳng thức.
Cách giải:
Ta có \(B = 3 + {3^2} + {3^3} + .... + {3^{2014}} + {3^{2015}}\) (1)
Nhân \(3\) vào hai vế của \(B\) ta được:
\(3B = 3\left( {3 + {3^2} + {3^3} + .... + {3^{2014}} + {3^{2015}}} \right) = 3.3 + {3.3^2} + {3.3^3} + ... + {3.3^{2014}} + {3.3^{2015}} = {3^2} + {3^3} + ... + {3^{2015}} + {3^{2016}}\) (2)
Lấy hai vế của (2) trừ hai vế tương ứng của (1) ta được:
\(\begin{array}{l}3B - B = \left( {{3^2} - {3^2}} \right) + \left( {{3^3} - {3^3}} \right) + .... + \left( {{3^{2014}} - {3^{2014}}} \right) + \left( {{3^{2015}} - {3^{2015}}} \right) + {3^{2016}} - 3\\2B = 0 + 0 + .... + {3^{2016}} - 3\\2B = {3^{2016}} - 3\end{array}\)
Suy ra \(2B + 3 = {3^{2016}}\)
Vậy \(2B + 3\) là một lũy thừa của \(3\).
Đề thi học kì 1 Toán 6 - Đề số 3 là một công cụ hữu ích cho học sinh trong quá trình ôn tập và chuẩn bị cho kỳ thi quan trọng. Đề thi bao gồm nhiều dạng bài tập khác nhau, từ các bài tập cơ bản đến các bài tập nâng cao, giúp học sinh rèn luyện kỹ năng giải toán một cách toàn diện.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi học kì 1 Toán 6 - Đề số 3 bao gồm:
Để giải đề thi học kì 1 Toán 6 - Đề số 3 một cách hiệu quả, học sinh cần:
Bài 1: Tính giá trị của biểu thức sau: (12 + 18) : 6
Giải:
(12 + 18) : 6 = 30 : 6 = 5
Luyện tập với đề thi học kì 1 Toán 6 - Đề số 3 mang lại nhiều lợi ích cho học sinh:
Để đạt kết quả tốt nhất trong kỳ thi học kì 1 Toán 6, học sinh nên:
Ngoài đề thi học kì 1 Toán 6 - Đề số 3, học sinh có thể tham khảo thêm các tài liệu sau:
Đề thi học kì 1 Toán 6 - Đề số 3 là một công cụ hỗ trợ đắc lực cho học sinh trong quá trình ôn tập và chuẩn bị cho kỳ thi. Chúc các em học sinh đạt kết quả tốt nhất!