Chào mừng các em học sinh lớp 6 đến với đề thi giữa kì 1 Toán 6 - Đề số 2 của giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn tập lại kiến thức đã học trong chương trình Toán 6, đồng thời làm quen với cấu trúc đề thi thực tế.
Với đề thi này, các em sẽ được rèn luyện các kỹ năng giải toán cơ bản, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Đề thi đi kèm với đáp án chi tiết, giúp các em tự đánh giá kết quả và rút kinh nghiệm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
A. PHẦN TRẮC NGHIỆM
1. A | 2. A | 3. C | 4. B | 5. A | 6. A |
7. C | 8. C | 9. A | 10. B | 11. C | 12. A |
Câu 1
Phương pháp
Sử dụng các kiến thức về tập hợp số tự nhiên
Cách giải
Số \(0\) là số tự nhiên nhỏ nhất.
Chọn A.
Câu 2
Phương pháp
Sử dụng cách viết tập hợp: nêu tính chất đặc trưng của tập hợp.
Cách giải
Ta có: \(\left\{ {x \in \mathbb{N}|3 < x \le 8} \right\}\)
Chọn A.
Câu 3
Phương pháp
Sử dụng phép tính chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}(m \ge n)\)
Cách giải
Ta có: \({3^7}:{3^5} = {3^{7 - 5}} = {3^2} = 9\)
Chọn C.
Câu 4
Phương pháp
Sử dụng phép tính nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\)
Cách giải
Ta có: \({6^2}{.6^5} = {6^{2 + 5}} = {6^7}\)
Chọn B.
Câu 5
Phương pháp
Đưa các số về dạng lũy thừa có cùng cơ số, sau đó so sánh số mũ.
Cách giải
Ta có: \({27^4} = {\left( {{3^3}} \right)^4} = {3^{3.4}} = {3^{12}}\); \({243^3} = {\left( {{3^5}} \right)^3} = {3^{5.3}} = {3^{15}}\)
Mà do 3 > 1 và 12 < 15 nên \({3^{12}} < {3^{15}} \Rightarrow {27^4} < {243^3}\)
Chọn A.
Câu 6
Phương pháp
Sử dụng quan hệ thứ tự thực hiện phép tính và tính lũy thừa của một số tự nhiên.
Cách giải
Ta có:
\(440:\left[ {65-{{\left( {14-9} \right)}^2}} \right] + {2021^0}\; \)
\(= 440:\left( {65 - {5^2}} \right) + 1 \)
\(= 440:\left( {65 - 25} \right) + 1 \)
\(= 440:40+ 1 \)
\(= 11 + 1 = 12\)
Chọn A.
Câu 7
Phương pháp
Thử từng giá trị của \(x\) trong tập cho trước.
Sử dụng dấu hiệu chia hết cho 5.
Cách giải
Ta có: \(56 - 23 = 33\) không chia hết cho \(5\).
\(56 - 24 = 32\) không chia hết cho \(5\).
\(56 - 25 = 31\) không chia hết cho \(5\).
\(56 - 26 = 30\) chia hết cho 5.
\(56 - 27 = 29\) không chia hết cho \(5\).
Chọn C.
Câu 8
Phương pháp
Sử dụng dấu hiệu chia hết cho \(2;3;5;9\).
Cách giải
Số chia hết cho \(2\) và \(5\) có chữ số tận cùng là \(0\).
Số chia hết cho \(2;3;5;9\) là \(1620\).
Chọn C.
Câu 9
Phương pháp
Từ công thức chu vi của hình vuông, ta tính được cạnh của hình vuông.
Áp dụng công thức tính diện tích hình vuông.
Cách giải
Độ dài cạnh của hình vuông là: \(12:4 = 3\) (cm)
Diện tích của hình vuông là: \(3.3 = 9\) (cm2)
Chọn A.
Câu 10
Phương pháp
Từ công thức diện tích hình chữ nhật, ta tính được độ dài cạnh còn lại.
Áp dụng công thức tính chu vi mảnh giấy hình chữ nhật.
Cách giải
Độ dài cạnh còn lại của hình chữ nhật là:
\(96:12 = 8\) (cm)
Chu vi mảnh giấy hình chữ nhật là: \(\left( {8 + 12} \right).2 = 40\) (cm)
Chọn B.
Câu 11
Phương pháp
Hình lục giác đều là lục giác có 6 cạnh bằng nhau, 6 góc bằng nhau
Cách giải
Hình C là hình lục giác đều.
Chọn A.
Câu 12
Phương pháp
Hình chữ nhật là tứ giác có 4 góc vuông
Cách giải
Các hình chữ nhật có đỉnh là đỉnh của lục giác là: ABDE; BCEF; AFDC
Chọn A
A. PHẦN TỰ LUẬN
Câu 1
Phương pháp
Sử dụng cách viết tập hợp bằng cách liệt kê các phần tử: Liệt kê các phần tử trong dấu { }, theo thứ tự tùy ý, mỗi phần tử chỉ được liệt kê 1 lần, ngăn cách với nhau bằng dấu ;
Cách giải
a) \({\rm{M = }}\left\{ {{\rm{x}} \in {\rm{N |1}} \le x < 10} \right\}\) và \({\rm{N}} = \left\{ {x \in {{\rm{N}}^*}|x < 6} \right\}\)
Ta có: \({\rm{M = }}\left\{ {{\rm{x}} \in {\rm{N| 1}} \le x < 10} \right\}\) \( \Rightarrow M = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\)
\({\rm{N}} = \left\{ {x \in {{\rm{N}}^*}|x < 6} \right\}\)\( \Rightarrow N = \left\{ {1;2;3;4;5} \right\}\)
c) \(2 \in M;\,10 \notin M;\,0 \notin N\)
Câu 2
Phương pháp
Sử dụng:
+ Dấu hiệu chia hết cho 5: Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho \(5\)
+ Tính chất chia hết của một tổng: Nếu \(a \vdots m;b \vdots m \Rightarrow \left( {a + b} \right) \vdots m\)
Cách giải
a) Ta có: \(1236\) có tổng các chữ số là \(1 + 2 + 3 + 6 = 12\) không chia hết cho \(9\) nên \(1236\) không chia hết cho \(9\). Và \(36\) chia hết cho \(9\).
Do đó \(1236 + 36\) không chia hết cho \(9\).
b) Ta có: \(15\) chia hết cho \(5\) và \(30\) chia hết cho \(5\) nên \(15 + 30\) chia hết cho \(5\).
\(17\) không chia hết cho \(5\) và \(30\) chia hết cho \(5\) nên \(17 + 30\) không chia hết cho \(5\).
\(29\)không chia hết cho \(5\) và \(30\) chia hết cho \(5\) nên \(29 + 30\) không chia hết cho \(5\).
\(60\) chia hết cho \(5\) và \(30\) chia hết cho \(5\) nên \(60 + 30\) chia hết cho \(5\)
Câu 3
a) \(\begin{array}{l}19.63 + 36.19 + 19\\ = 19\left( {63 + 36 + 1} \right)\\ = 19.100 = 1900\end{array}\) b) \(\begin{array}{l}{7^2} - 36:{3^2}\\ = 49 - 36:9\\ = 49 - 4 = 45\end{array}\) | c) \(476 - \left\{ {5\left[ {409 - {{\left( {8.3 - 21} \right)}^2}} \right] - 1724} \right\}\) \(\begin{array}{l} = 476 - \left[ {5\left( {409 - {3^2}} \right) - 1724} \right]\\ = 476 - \left( {5.400 - 1724} \right)\\ = 476 - 2000 + 1724\\ = 2200 - 2000 = 200\end{array}\) |
Câu 4
Phương pháp
Chuyển vế, sử dụng các phép tính cộng, trừ, nhân, chia để tìm \(x\).
Cách giải
a) \(41 - \left( {2x - 5} \right) = 18\) \(\begin{array}{l}2x - 5 = 41 - 18\\2x - 5 = 23\\2x = 23 + 5\\2x = 28\\x = 14\end{array}\) | b) \({2^x}.4 = 128\) \(\begin{array}{l}{2^x}{.2^2} = {2^7}\\{2^{x + 2}} = {2^7}\\x + 2 = 7\\x = 7 - 2\\x = 5\end{array}\) |
Vậy x = 14 | Vậy x = 5 |
Câu 5
Phương pháp
Từ đề bài ta rút ra được: Số giường nằm tại khu cách ly bằng tổng số giường nằm ở hai tòa nhà.
Cách giải
Tổng số giường nằm tại khu cách ly đó là:
\(50.8 + 36.4 = 544\) (giường nằm)
Vậy tổng có 544 giường nằm.
Câu 6
Phương pháp:
Vận dụng tính chất của hình thoi: hình thoi có 4 cạnh bằng nhau
Chu vi hình thoi = 4 . cạnh
Diện tích hình thoi = Tích 2 đường chéo : 2
Cách giải:
Ta có: \(ABCD\) là hình thoi (gt)
\( \Rightarrow AD = AB = BC = 5cm\) (mối quan hệ giữa các yếu tố trong hình thoi)
Chu vi hình thoi là:
C = 4 . AB = 4 . 5 = 20 (cm)
Diện tích hình thoi là:
S = AC . BD : 2 = 6 . 8 : 2= 24 (cm2)
Câu 1:Trong các khẳng định sau, khẳng định sai là
A. Số \(1\) là số tự nhiên nhỏ nhất;
B. Tập hợp các số tự nhiên có vô số phần tử;
C. Không có số tự nhiên lớn nhất;
D. Phần tử thuộc \(\mathbb{N}\) nhưng không thuộc \(\mathbb{N}^*\) là \(0\).
Câu 2: Tập hợp \(A\) các số tự nhiên lớn hơn 3 và không lớn hơn 8 là
A. \(\left\{ {x \in \mathbb{N}|3 < x \le 8} \right\}\); B. \(\left\{ {x \in \mathbb{N}|3 \le x \le 8} \right\}\); C. \(\left\{ {x \in \mathbb{N}|3 < x < 8} \right\}\); D. \(\left\{ {x \in \mathbb{N}|3 < x \le 9} \right\}\).
Câu 3: Kết quả của phép tính \({3^7}:{3^5}\)là
A. \(3\); B.\(1\);
C. \(9\); D. Một kết quả khác.
Câu 4: Trong các phép tính sau, phép tính đúng là
A. \({6^2}{.6^5} = {6^{10}}\); B. \({6^2}{.6^5} = {6^7}\); C. \({6^2}{.6^5} = {36^{10}}\); D. \({6^2}{.6^5} = {36^7}\).
Câu 5:Kết quả so sánh hai số \({27^4}\) và \({243^3}\) là
A.\({27^4} < {\rm{ }}{243^3}\); B.\(\;{27^4} > {\rm{ }}{243^3}\); C. \({27^4} = {\rm{ }}{243^3}\); D. \({27^4} \ge {243^3}\).
Câu 6:Kết quả phép tính \(440:\left[ {65-{{\left( {14-9} \right)}^2}} \right] + {2021^0}\;\) là
A. \(12\); B. \(9\);
C. \(11\); D. \(2032\).
Câu 7: Tìm x thuộc tập \(\left\{ {23;24;25;26;27} \right\}\), biết rằng \(56 - x\) chia hết cho 5. Giá trị của \(x\) thỏa mãn là
A. \(23\); B. \(25\); C. \(26\); D. \(27\).
Câu 8: Từ \(4\) chữ số\(\;1;0;2;6\) ta ghép được số chia hết cho \(2;3;5;9\) là
A. \(2106\); B.\(1062\); C.\(1620\); D. \(6201\).
Câu 9:Hình vuông có chu vi là \(12cm\) thì diện tích của hình vuông đó là
A. \(9c{m^2}\); B. \(6c{m^2}\); C. \(16c{m^2}\); D. \(36c{m^2}\).
Câu 10: Một mảnh giấy hình chữ nhật có diện tích \(96c{m^2}\), độ dài một cạnh là \(12cm\). Chu vi của mảnh giấy là
A. \(20cm\); B. \(40cm\); C. \(60cm\); D. \(80cm\).
Câu 11:Trong các hình dưới đây, chọn hình có xuất hiện lục giác đều
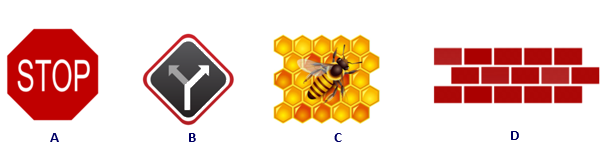
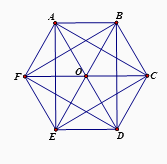
Câu 12: Số hình chữ nhật tạo bởi các đỉnh của hình lục giác đều sau là
A. \(3\);
B. \(4\);
C. \(5\);
D. Một đáp án khác.
B. PHẦN TỰ LUẬN (7 điểm)
Câu 1: ( 1 điểm) Cho hai tập hợp \({\rm{M = }}\left\{ {{\rm{x}} \in {\rm{N|1}} \le x < 10} \right\}\) và \({\rm{N}} = \left\{ {x \in {{\rm{N}}^*}|x < 6} \right\}\)
a) Viết các tập hợp M và tập hợp N bằng cách liệt kê các phần tử?
b) Điền các kí hiệu \( \in \); \( \notin \) vào các ô vuông sau:
2 □ M; 10 □ M; 0 □ N.
Câu 2: (1 điểm)
a) Không làm phép tính, hãy cho biết tổng \(\left( {1236 + 36} \right)\) có chia hết cho \(9\) không?
b) Áp dụng tính chất chia hết của một tổng, hãy tìm \(x\) thuộc tập \(\left\{ {15;17;29;60} \right\}\) sao cho \(x + 30\) chia hết cho \(5\)?
Câu 3: ( 1,5 điểm) Thực hiện phép tính (tính nhanh nếu có thể):
a) 19.63 + 36.19 + 19
b) 72 – 36 : 32
c) 476 – {5.[409 – (8.3 – 21)2] – 1724}.
Câu 4: (1 điểm) Tìm số tự nhiên x biết:
a) 41 – (2x – 5) = 18 b) 2x . 4 = 128
Câu 5: (1 điểm) Trong đợt dịch Covid 19 bùng phát lần thứ 4 tại Hà Nội, các trung tâm, tòa nhà trống thường được sử dụng làm khu cách ly tập trung. Tại khu cách ly của một huyện gồm có hai tòa nhà. Tòa A có 50 phòng, mỗi phòng có 8 giường; tòa B có 36 phòng, mỗi phòng có 4 giường. Hãy tính tổng số giường nằm tại khu cách ly đó?
Câu 6: (1,5 điểm)Cho hình thoi \(ABCD\). Biết \(AB = 5cm,AC = 6cm,BD = 8cm\). Tính \(AD,BC,CD\), chu vi và diện tích hình thoi ABCD?
Câu 1:Trong các khẳng định sau, khẳng định sai là
A. Số \(1\) là số tự nhiên nhỏ nhất;
B. Tập hợp các số tự nhiên có vô số phần tử;
C. Không có số tự nhiên lớn nhất;
D. Phần tử thuộc \(\mathbb{N}\) nhưng không thuộc \(\mathbb{N}^*\) là \(0\).
Câu 2: Tập hợp \(A\) các số tự nhiên lớn hơn 3 và không lớn hơn 8 là
A. \(\left\{ {x \in \mathbb{N}|3 < x \le 8} \right\}\); B. \(\left\{ {x \in \mathbb{N}|3 \le x \le 8} \right\}\); C. \(\left\{ {x \in \mathbb{N}|3 < x < 8} \right\}\); D. \(\left\{ {x \in \mathbb{N}|3 < x \le 9} \right\}\).
Câu 3: Kết quả của phép tính \({3^7}:{3^5}\)là
A. \(3\); B.\(1\);
C. \(9\); D. Một kết quả khác.
Câu 4: Trong các phép tính sau, phép tính đúng là
A. \({6^2}{.6^5} = {6^{10}}\); B. \({6^2}{.6^5} = {6^7}\); C. \({6^2}{.6^5} = {36^{10}}\); D. \({6^2}{.6^5} = {36^7}\).
Câu 5:Kết quả so sánh hai số \({27^4}\) và \({243^3}\) là
A.\({27^4} < {\rm{ }}{243^3}\); B.\(\;{27^4} > {\rm{ }}{243^3}\); C. \({27^4} = {\rm{ }}{243^3}\); D. \({27^4} \ge {243^3}\).
Câu 6:Kết quả phép tính \(440:\left[ {65-{{\left( {14-9} \right)}^2}} \right] + {2021^0}\;\) là
A. \(12\); B. \(9\);
C. \(11\); D. \(2032\).
Câu 7: Tìm x thuộc tập \(\left\{ {23;24;25;26;27} \right\}\), biết rằng \(56 - x\) chia hết cho 5. Giá trị của \(x\) thỏa mãn là
A. \(23\); B. \(25\); C. \(26\); D. \(27\).
Câu 8: Từ \(4\) chữ số\(\;1;0;2;6\) ta ghép được số chia hết cho \(2;3;5;9\) là
A. \(2106\); B.\(1062\); C.\(1620\); D. \(6201\).
Câu 9:Hình vuông có chu vi là \(12cm\) thì diện tích của hình vuông đó là
A. \(9c{m^2}\); B. \(6c{m^2}\); C. \(16c{m^2}\); D. \(36c{m^2}\).
Câu 10: Một mảnh giấy hình chữ nhật có diện tích \(96c{m^2}\), độ dài một cạnh là \(12cm\). Chu vi của mảnh giấy là
A. \(20cm\); B. \(40cm\); C. \(60cm\); D. \(80cm\).
Câu 11:Trong các hình dưới đây, chọn hình có xuất hiện lục giác đều
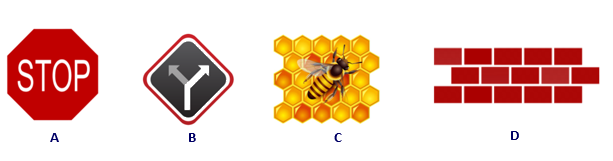
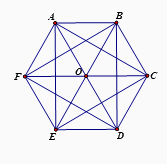
Câu 12: Số hình chữ nhật tạo bởi các đỉnh của hình lục giác đều sau là
A. \(3\);
B. \(4\);
C. \(5\);
D. Một đáp án khác.
B. PHẦN TỰ LUẬN (7 điểm)
Câu 1: ( 1 điểm) Cho hai tập hợp \({\rm{M = }}\left\{ {{\rm{x}} \in {\rm{N|1}} \le x < 10} \right\}\) và \({\rm{N}} = \left\{ {x \in {{\rm{N}}^*}|x < 6} \right\}\)
a) Viết các tập hợp M và tập hợp N bằng cách liệt kê các phần tử?
b) Điền các kí hiệu \( \in \); \( \notin \) vào các ô vuông sau:
2 □ M; 10 □ M; 0 □ N.
Câu 2: (1 điểm)
a) Không làm phép tính, hãy cho biết tổng \(\left( {1236 + 36} \right)\) có chia hết cho \(9\) không?
b) Áp dụng tính chất chia hết của một tổng, hãy tìm \(x\) thuộc tập \(\left\{ {15;17;29;60} \right\}\) sao cho \(x + 30\) chia hết cho \(5\)?
Câu 3: ( 1,5 điểm) Thực hiện phép tính (tính nhanh nếu có thể):
a) 19.63 + 36.19 + 19
b) 72 – 36 : 32
c) 476 – {5.[409 – (8.3 – 21)2] – 1724}.
Câu 4: (1 điểm) Tìm số tự nhiên x biết:
a) 41 – (2x – 5) = 18 b) 2x . 4 = 128
Câu 5: (1 điểm) Trong đợt dịch Covid 19 bùng phát lần thứ 4 tại Hà Nội, các trung tâm, tòa nhà trống thường được sử dụng làm khu cách ly tập trung. Tại khu cách ly của một huyện gồm có hai tòa nhà. Tòa A có 50 phòng, mỗi phòng có 8 giường; tòa B có 36 phòng, mỗi phòng có 4 giường. Hãy tính tổng số giường nằm tại khu cách ly đó?
Câu 6: (1,5 điểm)Cho hình thoi \(ABCD\). Biết \(AB = 5cm,AC = 6cm,BD = 8cm\). Tính \(AD,BC,CD\), chu vi và diện tích hình thoi ABCD?
A. PHẦN TRẮC NGHIỆM
1. A | 2. A | 3. C | 4. B | 5. A | 6. A |
7. C | 8. C | 9. A | 10. B | 11. C | 12. A |
Câu 1
Phương pháp
Sử dụng các kiến thức về tập hợp số tự nhiên
Cách giải
Số \(0\) là số tự nhiên nhỏ nhất.
Chọn A.
Câu 2
Phương pháp
Sử dụng cách viết tập hợp: nêu tính chất đặc trưng của tập hợp.
Cách giải
Ta có: \(\left\{ {x \in \mathbb{N}|3 < x \le 8} \right\}\)
Chọn A.
Câu 3
Phương pháp
Sử dụng phép tính chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}(m \ge n)\)
Cách giải
Ta có: \({3^7}:{3^5} = {3^{7 - 5}} = {3^2} = 9\)
Chọn C.
Câu 4
Phương pháp
Sử dụng phép tính nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\)
Cách giải
Ta có: \({6^2}{.6^5} = {6^{2 + 5}} = {6^7}\)
Chọn B.
Câu 5
Phương pháp
Đưa các số về dạng lũy thừa có cùng cơ số, sau đó so sánh số mũ.
Cách giải
Ta có: \({27^4} = {\left( {{3^3}} \right)^4} = {3^{3.4}} = {3^{12}}\); \({243^3} = {\left( {{3^5}} \right)^3} = {3^{5.3}} = {3^{15}}\)
Mà do 3 > 1 và 12 < 15 nên \({3^{12}} < {3^{15}} \Rightarrow {27^4} < {243^3}\)
Chọn A.
Câu 6
Phương pháp
Sử dụng quan hệ thứ tự thực hiện phép tính và tính lũy thừa của một số tự nhiên.
Cách giải
Ta có:
\(440:\left[ {65-{{\left( {14-9} \right)}^2}} \right] + {2021^0}\; \)
\(= 440:\left( {65 - {5^2}} \right) + 1 \)
\(= 440:\left( {65 - 25} \right) + 1 \)
\(= 440:40+ 1 \)
\(= 11 + 1 = 12\)
Chọn A.
Câu 7
Phương pháp
Thử từng giá trị của \(x\) trong tập cho trước.
Sử dụng dấu hiệu chia hết cho 5.
Cách giải
Ta có: \(56 - 23 = 33\) không chia hết cho \(5\).
\(56 - 24 = 32\) không chia hết cho \(5\).
\(56 - 25 = 31\) không chia hết cho \(5\).
\(56 - 26 = 30\) chia hết cho 5.
\(56 - 27 = 29\) không chia hết cho \(5\).
Chọn C.
Câu 8
Phương pháp
Sử dụng dấu hiệu chia hết cho \(2;3;5;9\).
Cách giải
Số chia hết cho \(2\) và \(5\) có chữ số tận cùng là \(0\).
Số chia hết cho \(2;3;5;9\) là \(1620\).
Chọn C.
Câu 9
Phương pháp
Từ công thức chu vi của hình vuông, ta tính được cạnh của hình vuông.
Áp dụng công thức tính diện tích hình vuông.
Cách giải
Độ dài cạnh của hình vuông là: \(12:4 = 3\) (cm)
Diện tích của hình vuông là: \(3.3 = 9\) (cm2)
Chọn A.
Câu 10
Phương pháp
Từ công thức diện tích hình chữ nhật, ta tính được độ dài cạnh còn lại.
Áp dụng công thức tính chu vi mảnh giấy hình chữ nhật.
Cách giải
Độ dài cạnh còn lại của hình chữ nhật là:
\(96:12 = 8\) (cm)
Chu vi mảnh giấy hình chữ nhật là: \(\left( {8 + 12} \right).2 = 40\) (cm)
Chọn B.
Câu 11
Phương pháp
Hình lục giác đều là lục giác có 6 cạnh bằng nhau, 6 góc bằng nhau
Cách giải
Hình C là hình lục giác đều.
Chọn A.
Câu 12
Phương pháp
Hình chữ nhật là tứ giác có 4 góc vuông
Cách giải
Các hình chữ nhật có đỉnh là đỉnh của lục giác là: ABDE; BCEF; AFDC
Chọn A
A. PHẦN TỰ LUẬN
Câu 1
Phương pháp
Sử dụng cách viết tập hợp bằng cách liệt kê các phần tử: Liệt kê các phần tử trong dấu { }, theo thứ tự tùy ý, mỗi phần tử chỉ được liệt kê 1 lần, ngăn cách với nhau bằng dấu ;
Cách giải
a) \({\rm{M = }}\left\{ {{\rm{x}} \in {\rm{N |1}} \le x < 10} \right\}\) và \({\rm{N}} = \left\{ {x \in {{\rm{N}}^*}|x < 6} \right\}\)
Ta có: \({\rm{M = }}\left\{ {{\rm{x}} \in {\rm{N| 1}} \le x < 10} \right\}\) \( \Rightarrow M = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\)
\({\rm{N}} = \left\{ {x \in {{\rm{N}}^*}|x < 6} \right\}\)\( \Rightarrow N = \left\{ {1;2;3;4;5} \right\}\)
c) \(2 \in M;\,10 \notin M;\,0 \notin N\)
Câu 2
Phương pháp
Sử dụng:
+ Dấu hiệu chia hết cho 5: Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho \(5\)
+ Tính chất chia hết của một tổng: Nếu \(a \vdots m;b \vdots m \Rightarrow \left( {a + b} \right) \vdots m\)
Cách giải
a) Ta có: \(1236\) có tổng các chữ số là \(1 + 2 + 3 + 6 = 12\) không chia hết cho \(9\) nên \(1236\) không chia hết cho \(9\). Và \(36\) chia hết cho \(9\).
Do đó \(1236 + 36\) không chia hết cho \(9\).
b) Ta có: \(15\) chia hết cho \(5\) và \(30\) chia hết cho \(5\) nên \(15 + 30\) chia hết cho \(5\).
\(17\) không chia hết cho \(5\) và \(30\) chia hết cho \(5\) nên \(17 + 30\) không chia hết cho \(5\).
\(29\)không chia hết cho \(5\) và \(30\) chia hết cho \(5\) nên \(29 + 30\) không chia hết cho \(5\).
\(60\) chia hết cho \(5\) và \(30\) chia hết cho \(5\) nên \(60 + 30\) chia hết cho \(5\)
Câu 3
a) \(\begin{array}{l}19.63 + 36.19 + 19\\ = 19\left( {63 + 36 + 1} \right)\\ = 19.100 = 1900\end{array}\) b) \(\begin{array}{l}{7^2} - 36:{3^2}\\ = 49 - 36:9\\ = 49 - 4 = 45\end{array}\) | c) \(476 - \left\{ {5\left[ {409 - {{\left( {8.3 - 21} \right)}^2}} \right] - 1724} \right\}\) \(\begin{array}{l} = 476 - \left[ {5\left( {409 - {3^2}} \right) - 1724} \right]\\ = 476 - \left( {5.400 - 1724} \right)\\ = 476 - 2000 + 1724\\ = 2200 - 2000 = 200\end{array}\) |
Câu 4
Phương pháp
Chuyển vế, sử dụng các phép tính cộng, trừ, nhân, chia để tìm \(x\).
Cách giải
a) \(41 - \left( {2x - 5} \right) = 18\) \(\begin{array}{l}2x - 5 = 41 - 18\\2x - 5 = 23\\2x = 23 + 5\\2x = 28\\x = 14\end{array}\) | b) \({2^x}.4 = 128\) \(\begin{array}{l}{2^x}{.2^2} = {2^7}\\{2^{x + 2}} = {2^7}\\x + 2 = 7\\x = 7 - 2\\x = 5\end{array}\) |
Vậy x = 14 | Vậy x = 5 |
Câu 5
Phương pháp
Từ đề bài ta rút ra được: Số giường nằm tại khu cách ly bằng tổng số giường nằm ở hai tòa nhà.
Cách giải
Tổng số giường nằm tại khu cách ly đó là:
\(50.8 + 36.4 = 544\) (giường nằm)
Vậy tổng có 544 giường nằm.
Câu 6
Phương pháp:
Vận dụng tính chất của hình thoi: hình thoi có 4 cạnh bằng nhau
Chu vi hình thoi = 4 . cạnh
Diện tích hình thoi = Tích 2 đường chéo : 2
Cách giải:
Ta có: \(ABCD\) là hình thoi (gt)
\( \Rightarrow AD = AB = BC = 5cm\) (mối quan hệ giữa các yếu tố trong hình thoi)
Chu vi hình thoi là:
C = 4 . AB = 4 . 5 = 20 (cm)
Diện tích hình thoi là:
S = AC . BD : 2 = 6 . 8 : 2= 24 (cm2)
Đề thi giữa kì 1 Toán 6 - Đề số 2 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kỳ đầu tiên. Đề thi thường bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã được học trong chương trình Toán 6.
Cấu trúc đề thi có thể khác nhau tùy theo từng trường và giáo viên, nhưng thường bao gồm các phần sau:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 6, học sinh cần:
Dưới đây là một số ví dụ về các dạng bài tập thường xuất hiện trong đề thi giữa kì 1 Toán 6:
Ví dụ: Tính giá trị của biểu thức: 123 + 456 - 789
Ví dụ: Tìm phân số bằng phân số 2/3 và có mẫu số là 12.
Ví dụ: Một cửa hàng bán một chiếc áo với giá 150.000 đồng. Nếu cửa hàng giảm giá 10% thì giá chiếc áo sau khi giảm là bao nhiêu?
Ví dụ: Trong một lớp học có 30 học sinh, trong đó có 12 học sinh nữ. Tính tỉ số phần trăm của học sinh nữ trong lớp.
Việc ôn tập và luyện đề là vô cùng quan trọng để chuẩn bị cho kỳ thi giữa kì 1 Toán 6. Khi luyện đề, học sinh sẽ làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự đánh giá được trình độ của mình. Điều này giúp học sinh tự tin hơn khi bước vào phòng thi và đạt kết quả tốt nhất.
Đề thi giữa kì 1 Toán 6 - Đề số 2 là một cơ hội tốt để học sinh kiểm tra và củng cố kiến thức đã học. Bằng cách ôn tập kỹ lưỡng, luyện tập thường xuyên và áp dụng các kỹ năng làm bài thi hiệu quả, các em học sinh sẽ đạt được kết quả tốt nhất trong kỳ thi này.