Chào mừng các em học sinh đến với Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 7 tại giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong chương trình Toán 6, chương trình Kết nối tri thức.
Đề thi bao gồm các dạng bài tập đa dạng, bám sát nội dung sách giáo khoa và cấu trúc đề thi giữa kì.
Trong cách viết sau, cách viết nào cho ta phân số?
Số đối của phân số \( - \frac{{16}}{{25}}\) là:
Phân số nào sau đây bằng phân số \(\frac{3}{4}\)?
Tìm số nguyên \(y\) biết \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\).
Số \(3,148\) được làm tròn đến hàng phần chục?
Phân số \(\frac{{ - 31}}{{10}}\) được viết dưới dạng số thập phân?
Tính \(25\% \) của \(20\)?
Kết quả phép tính \(1,3 + 3,4 - 4,7 + 5,6 - 4,3\) là:
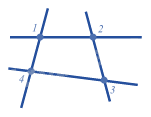
Cho hình vẽ

Số giao điểm tạo bởi 4 đường thẳng trong hình trên là:
Chọn phát biểu đúng trong các phát biểu sau:
Qua 2 điểm phân biệt ta vẽ được:
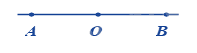
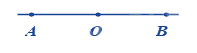
Chohình vẽ. Hai tia nào đối nhau?
Trong hình vẽ sau đây có bao nhiêu đoạn thẳng?

Thực hiện các phép tính (tính hợp lí nếu có thể):
a) A = \(\frac{1}{2}\)+\(\frac{1}{3}\)
b) \(B = \;6,3 + \left( { - {\rm{ }}6,3} \right) + 4,9\)
c) \(C = \frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}\)s
Tìm x, biết: \(\)
a) \(x - 5,01 = 7,02 - 3\;\)
b) \(\,\frac{1}{5} - \left( {\frac{2}{3} - x} \right) = \frac{{ - 3}}{5}\)
Một đám đất hình chữ nhật có chiều rộng 60m, chiều dài bằng \(\frac{4}{3}\) chiều rộng. Người ta để \(\frac{7}{{12}}\)diện tích đám đất đó trồng cây, \(30\% \) diện tích còn lại đó để đào ao thả cá. Diện tích ao bằng bao nhiêu phần trăm diện tích cả đám đất?
Cho \(Ox\) và \(Oy\) là hai tia đối nhau. Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA = 6cm\). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB = 3cm\). Gọi \(M,N\) lần lượt là trung điểm của \(OA,OB\).
a) Tính \(OM,{\rm{ }}ON\)?
b) Tính độ dài đoạn thẳng \(MN\)?
a) Tính tổng \(A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}}\).
b) Chứng minh \(M = \frac{{n - 1}}{{n - 2}}\,\,\,\left( {n \in {\rm Z}\,;\,n \ne 2} \right)\) là phân số tối giản.
Trong cách viết sau, cách viết nào cho ta phân số?
Đáp án : A
Dựa vào khái niệm về phân số.
\(\frac{{0,25}}{{ - 3}}\) không phải phân số vì \(0,25 \notin \mathbb{Z}\).
\(\frac{5}{0}\) không phải phân số vì 0 nằm ở mẫu.
\(\frac{{6,23}}{{7,4}}\) không phải phân số vì \(6,23;7,4 \notin \mathbb{Z}\).
\(\frac{4}{7}\) là phân số vì \(4;7 \in \mathbb{Z};7 \ne 0\).
Đáp án A.
Số đối của phân số \( - \frac{{16}}{{25}}\) là:
Đáp án : A
Số đối của phân số \(\frac{a}{b}\) là phân số \( - \frac{a}{b}\).
Số đối của phân số \( - \frac{{16}}{{25}}\) là\(\frac{{16}}{{25}}\).
Đáp án A.
Phân số nào sau đây bằng phân số \(\frac{3}{4}\)?
Đáp án : C
Sử dụng quy tắc nhân cả tử và mẫu của một phân số: Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
Ta có: \(\frac{3}{4} = \frac{{3.2}}{{4.2}} = \frac{6}{8}\) nên phân số \(\frac{6}{8} = \frac{3}{4}\).
Đáp án C.
Tìm số nguyên \(y\) biết \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\).
Đáp án : D
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) nếu ad = bc.
Ta có: \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\) nên
\(\begin{array}{l}2.\left( { - y} \right) = 6.\left( { - 3} \right)\\ - 2y = - 18\\y=(-18):(-2)\\y = 9\end{array}\)
Đáp án D.
Số \(3,148\) được làm tròn đến hàng phần chục?
Đáp án : B
Dựa vào quy tắc làm tròn số.
Số \(3,148\) được làm tròn đến hàng phần chục là 3,1.
Đáp án B.
Phân số \(\frac{{ - 31}}{{10}}\) được viết dưới dạng số thập phân?
Đáp án : D
Dựa vào kiến thức về số thập phân.
Phân số \(\frac{{ - 31}}{{10}}\) được viết dưới dạng số thập phân là -3,1.
Đáp án D.
Tính \(25\% \) của \(20\)?
Đáp án : B
Muốn tìm giá trị a% của số b, ta tính: \(b.a\% = b.\frac{a}{{100}}\).
25% của 20 là: \(20.25\% = 20.\frac{{25}}{{100}} = 20.\frac{1}{4} = 5\).
Đáp án B.
Kết quả phép tính \(1,3 + 3,4 - 4,7 + 5,6 - 4,3\) là:
Đáp án : A
Dựa vào quy tắc cộng, trừ số thập phân.
Ta có:
\(\begin{array}{l}1,3 + 3,4 - 4,7 + 5,6 - 4,3\\ = 1,3 + \left( {3,4 + 5,6} \right) - \left( {4,7 + 4,3} \right)\\ = 1,3 + 9 - 9\\ = 1,3\end{array}\)
Đáp án A.
Cho hình vẽ

Số giao điểm tạo bởi 4 đường thẳng trong hình trên là:
Đáp án : D
Quan sát hình vẽ để trả lời.
Có 4 giao điểm tạo bởi 4 đường thẳng trong hình trên.
Đáp án D.
Chọn phát biểu đúng trong các phát biểu sau:
Qua 2 điểm phân biệt ta vẽ được:
Đáp án : A
Dựa vào kiến thức về điểm và đường thẳng.
Qua hai điểm phân biệt ta chỉ vẽ được 1 đường thẳng nên A đúng.
Đáp án A.
Chohình vẽ. Hai tia nào đối nhau?
Đáp án : A
Dựa vào kiến thức về tia.
Hai tia OA và OB là hai tia đối nhau.
Đáp án A.
Trong hình vẽ sau đây có bao nhiêu đoạn thẳng?

Đáp án : D
Dựa vào kiến thức về đoạn thẳng.
Có 6 đoạn thẳng trong hình vẽ, đó là: KJ, KL, KN, JL, JN, LN.
Đáp án D.
Thực hiện các phép tính (tính hợp lí nếu có thể):
a) A = \(\frac{1}{2}\)+\(\frac{1}{3}\)
b) \(B = \;6,3 + \left( { - {\rm{ }}6,3} \right) + 4,9\)
c) \(C = \frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}\)s
Dựa vào các quy tắc tính với phân số và số thập phân.
a) A = \(\frac{1}{2}\) + \(\frac{1}{3}\) = \(\frac{3}{6} + \frac{2}{6} = \frac{5}{6}\)
b) B = 6,3 + (-6,3) + 4,9 = [6,3 + (-6,3)] + 4,9 = 0 + 4,9 = 4,9
c) \(C = \frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}\)\( = \left( {\frac{{ - 3}}{7} - \frac{4}{7}} \right) + \left( {\frac{5}{{14}} + \frac{9}{{14}}} \right) + \frac{3}{{12}}\) \( = - 1 + 1 + \frac{3}{{12}}\) \( = \frac{3}{{12}}\) = \(\frac{1}{4}\)
Tìm x, biết: \(\)
a) \(x - 5,01 = 7,02 - 3\;\)
b) \(\,\frac{1}{5} - \left( {\frac{2}{3} - x} \right) = \frac{{ - 3}}{5}\)
Dựa vào quy tắc tính với phân số và số thập phân để tìm x.
a) x - 5,01 = 7,02 - 3
x - 5,01 = 4,02
x = 4,02 + 5,01
x = 9,03
Vậy \(x = 9,03\)
b) \(\frac{1}{5} - \left( {\frac{2}{3} - x} \right) = \frac{{ - 3}}{5}\)
\(\frac{2}{3} - x = \frac{1}{5} - \frac{{ - 3}}{5}\)
\(x = \frac{2}{3} - \frac{4}{5}\)
Vậy x = \(\frac{{ - 2}}{{15}}\)
Một đám đất hình chữ nhật có chiều rộng 60m, chiều dài bằng \(\frac{4}{3}\) chiều rộng. Người ta để \(\frac{7}{{12}}\)diện tích đám đất đó trồng cây, \(30\% \) diện tích còn lại đó để đào ao thả cá. Diện tích ao bằng bao nhiêu phần trăm diện tích cả đám đất?
Sử dụng các phép tính với phân số và tỉ số phần trăm để tìm tính chiều dài đám đất, diện tích trồng cây, diên tích ao cá.
Sử dụng công thức tính diện tích hình chữ nhật để tính diện tích đám đất.
Tính diện tích ao bằng bao nhiêu phần trăm diện tích cả đám đất bằng công thức:
Diện tích ao : diện tích cả đám đất . 100.
Chiều dài đám đất là: \(60.\frac{4}{3} = 80\)(m)
Diện tích đám đất là: \(60.80 = 4800\)(m2)
Diện tích trồng cây là: \(4800.\frac{7}{{12}} = 2800\)(m2)
Diện tích đất còn lại sau khi trồng cây là: \(4800 - 2800 = 2000\)(m)
Diện tích ao cá: \(2000.30\% = 600\)(m2)
Diện tích ao bằng: \(600:4800 = {\rm{ }}0,125{\rm{ }} = 12,5\% \).
Vậy diện tích ao bằng 12,5% diện tích đám đất
Cho \(Ox\) và \(Oy\) là hai tia đối nhau. Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA = 6cm\). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB = 3cm\). Gọi \(M,N\) lần lượt là trung điểm của \(OA,OB\).
a) Tính \(OM,{\rm{ }}ON\)?
b) Tính độ dài đoạn thẳng \(MN\)?
Vẽ hình theo yêu cầu đề bài.
a) Sử dụng tính chất của trung điểm để tìm OM, ON.
b) Vì O nằm giữa MN nên MN = OM + ON.

a) Do \(M\) là trung điểm của \(OA\) nên ta có:
\(OM = MA = \frac{{OA}}{2} = \frac{6}{2} = 3(cm)\)
Do \(N\) là trung điểm của \(OB\) nên ta có:
\(ON = NB = \frac{{OB}}{2} = \frac{3}{2} = 1,5(cm)\)
b) Vì điểm \(O\) nằm giữa hai điểm \(M,N\) nên ta có: \(MN = OM + ON\)
Suy ra \(MN = 3 + 1,5 = 4,5(cm)\)
Vậy \({\rm{MN = 4,5 cm}}\).
a) Tính tổng \(A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}}\).
b) Chứng minh \(M = \frac{{n - 1}}{{n - 2}}\,\,\,\left( {n \in {\rm Z}\,;\,n \ne 2} \right)\) là phân số tối giản.
a) Nhân cả tử và mẫu của các phân số trong A với 2.
Rút 2 ra ngoài, biến đổi các phân số \(\frac{1}{{a\left( {a + 1} \right)}}\) thành \(\frac{1}{a} - \frac{1}{{a + 1}}\) (vì \(\frac{1}{{a\left( {a + 1} \right)}} = \frac{1}{a} - \frac{1}{{a + 1}}\))
Tính A.
b) Để chứng minh phân số tổi giản, ta chứng minh ƯCLN của tử số và mẫu số là 1.
a) Ta có \(A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}} = \frac{2}{6} + \frac{2}{{12}} + \frac{2}{{20}} + \frac{2}{{30}} + ... + \frac{2}{{90}}\)
\(\begin{array}{l} = 2\left( {\frac{1}{{2.3}} + \frac{1}{{3.4}} + \frac{1}{{4.5}} + \frac{1}{{5.6}} + ... + \frac{1}{{9.10}}} \right)\\ = 2\left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + \frac{1}{5} - \frac{1}{6} + ... + \frac{1}{9} - \frac{1}{{10}}} \right)\end{array}\)
\( = 2\left( {\frac{1}{2} - \frac{1}{{10}}} \right) = 2.\frac{4}{{10}} = \frac{4}{5}\).
Vậy \(A = \frac{4}{5}.\)
b) Gọi ƯCLN\(\left( {n - 1\,;\,n - 2} \right) = d\) suy ra \(n - 1 \vdots d\,\,\,,\,\,n - 2 \vdots d\)
suy ra \(\left( {n - 1} \right) - \left( {n - 2} \right) \vdots d\)suy ra \(1 \vdots d \Rightarrow d = 1\) với mọi \(n\)
Vậy với mọi \(n \in {\rm Z}\) thì \(M = \frac{{n - 1}}{{n - 2}}\) là phân số tối giản.
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 7 là một công cụ quan trọng giúp học sinh lớp 6 đánh giá năng lực và kiến thức đã học trong giai đoạn giữa học kỳ. Đề thi này không chỉ kiểm tra khả năng tính toán mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp một cái nhìn tổng quan về đề thi, phân tích các dạng bài tập thường gặp và hướng dẫn giải chi tiết để giúp học sinh tự tin hơn khi làm bài.
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 7 thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Các bài tập về số nguyên thường yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia số nguyên, so sánh số nguyên và tìm giá trị tuyệt đối của số nguyên. Để giải các bài tập này, học sinh cần nắm vững các quy tắc về phép toán với số nguyên.
Ví dụ: Tính (-5) + 3 - (-2) = ?
Giải: (-5) + 3 - (-2) = -5 + 3 + 2 = 0
Các bài tập về phân số thường yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia phân số, so sánh phân số và rút gọn phân số. Để giải các bài tập này, học sinh cần nắm vững các quy tắc về phép toán với phân số và hiểu rõ khái niệm phân số tối giản.
Ví dụ: Tính 1/2 + 1/3 = ?
Giải: 1/2 + 1/3 = 3/6 + 2/6 = 5/6
Các bài tập về tỉ số và phần trăm thường yêu cầu học sinh tính tỉ số của hai đại lượng, tính phần trăm của một đại lượng và giải các bài toán liên quan đến tỉ lệ. Để giải các bài tập này, học sinh cần hiểu rõ khái niệm tỉ số và phần trăm và biết cách chuyển đổi giữa chúng.
Ví dụ: Một lớp có 30 học sinh, trong đó có 12 học sinh nữ. Tính tỉ số phần trăm học sinh nữ trong lớp.
Giải: Tỉ số phần trăm học sinh nữ trong lớp là: (12/30) * 100% = 40%
Các bài tập về hình học cơ bản thường yêu cầu học sinh xác định các loại góc, tính độ dài đoạn thẳng, vẽ hình và giải các bài toán liên quan đến các tính chất của hình học. Để giải các bài tập này, học sinh cần nắm vững các định nghĩa và tính chất cơ bản của hình học.
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 7 là một cơ hội tốt để học sinh rèn luyện kiến thức và kỹ năng giải toán. Bằng cách nắm vững các kiến thức cơ bản, luyện tập thường xuyên và áp dụng các phương pháp giải bài hiệu quả, các em học sinh có thể tự tin đạt kết quả tốt trong kỳ thi sắp tới. Chúc các em học sinh thành công!