Chào mừng các em học sinh lớp 6 đến với đề thi giữa kì 1 Toán 6 - Đề số 12 của giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn luyện và củng cố kiến thức đã học trong chương trình Toán 6, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Đề thi bao gồm các dạng bài tập đa dạng, từ cơ bản đến nâng cao, giúp các em làm quen với nhiều dạng câu hỏi khác nhau và rèn luyện kỹ năng giải toán.
Phần trắc nghiệm Câu 1. Tính chất nào KHÔNG phải là tính chất của phép nhân:
Phần trắc nghiệm
Câu 1. Tính chất nào KHÔNG phải là tính chất của phép nhân:
A. \(a \cdot b = b \cdot a\)
B. \(a \cdot \left( {b + c} \right) = ab + ac\)
C. \(a \cdot 1 = 1 \cdot a = a\)
D. \(a + 0 = 0 + a = a\)
Câu 2. Kết quả của phép tính \({5^3}:5\) là:
A. \({5^4}\)
B. \({5^3}\)
C. 25
D. 5
Câu 3. Số tự nhiên \(x\) thỏa mãn \({3^x} = 9\) là:
A. \(x = 4\)
B. \(x = 3\)
C. \(x = 2\)
D. \(x = 1\)
Câu 4. Giá trị của \(x\) thỏa mãn \(32:\left( {x - 32} \right) + 4 = 20\) là:
A. \(x = 16\)
B. \(x = 34\)
C. \(x = 32\)
D. \(x = 2\)
Câu 5. Kết quả của phép tính \(17.25 + 23.25 + 25.60\) là:
A. 2500
B. 25
C. 250
D. 25000
Câu 6. Chọn khẳng định SAI trong các khẳng định sau:
A. \(4x\) chia hết cho 4
B. \(16 + 24\) chia hết cho 4
C. \(256 - 72\) chia hết cho 4
D. \(29 + 136\) chia hết cho 4
Câu 7. Số tự nhiên \(a,b\) thỏa mãn \(\overline {a5b} \) chia hết cho cho \(2;5;9\) là
A. \(a = 5;b = 0\)
B. \(a = 5;b = 5\)
C. \(a = 9;b = 4\)
D. \(a = 4;b = 0\)
Câu 8. Trong các số sau: \(123;256;448;250;513\) số chia hết cho 3 là:
A. \(123;513\)
B. \(256;448;250\)
C. 250
D. \(448;256\)
Câu 9. Trong các hình dưới đây, hình nào là tam giác đều:

A. Hình a
B. Hình b
C. Hình c
D. Hình d
Câu 10. Tổng số đường chéo của hình lục giác\(ABCDEF\)là:
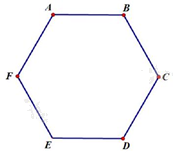
A. 8
B. 9
C. 10
D. 11
Phần tự luận
Bài 1.
a) Cho tập hợp \(A = \left\{ {1;2;3;5} \right\}\).
Điền kí hiệu \( \in , \notin \) thích hợp vào ô trống: $2 ... A; 4 ... A$
b) Tập hợp A bao gồm các số tự nhiên lớn hơn 8 và nhỏ hơn 12. Viết lại A theo 2 cách.
Bài 2. Thực hiện phép tính (tính hợp lí nếu có thể).
a) \(17 + 28 + 33 + 72\)
b) \({2^3}.17 - {2^3}.12\)
c) \(2022 - \left[ {2021 - {{(5 + 1)}^2}} \right] + {2023^0}\)
Bài 3. Tìm số tự nhiên \(x\) biết
a) \(192 - x = 16\)
b) \(69 + \left( {x + 16} \right) = 185\)
c) \(\left[ {{{(x - 1)}^3} - {4^2}} \right] \cdot 3 = 327\)
Bài 4. Một căn phòng hình chữ nhật có chiều rộng 3 m, chiều dài 6 m. Tính chu vi và diện tích của căn phòng. Người ta lát nền nhà bằng các viên gạch hình vuông có chiều dài cạnh 30 cm. Biết giá tiền một viên gạch là 25 000 đồng. Hỏi để lát hết nền nhà cần bao nhiêu tiền?
Bài 5. Tìm số tự nhiên n để \(\left( {4n + 8} \right):\left( {3n + 2} \right)\left( {n \ge 1} \right)\).
-------- Hết --------
Phần trắc nghiệm
1.D | 2.C | 3.C | 4.B | 5.A | 6.D | 7.D | 8.A | 9.C | 10.B |
Câu 1. Tính chất nào KHÔNG phải là tính chất của phép nhân:
A. \(a \cdot b = b \cdot a\)
B. \(a \cdot \left( {b + c} \right) = ab + ac\)
C. \(a \cdot 1 = 1 \cdot a = a\)
D. \(a + 0 = 0 + a = a\)
Phương pháp:
Nhận biết các tính chất cơ bản của phép nhân.
Lời giải:
\(a + 0 = 0 + a = a\) là tính chất của phép cộng, không phải phép nhân.
Đáp án D.
Câu 2. Kết quả của phép tính \({5^3}:5\) là:
A. \({5^4}\)
B. \({5^3}\)
C. 25
D. 5
Phương pháp:
Sử dụng công thức chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\)
Lời giải:
\({5^3}:5 = {5^2} = 25\)
Đáp án C.
Câu 3. Số tự nhiên \(x\) thỏa mãn \({3^x} = 9\) là:
A. \(x = 4\)
B. \(x = 3\)
C. \(x = 2\)
D. \(x = 1\)
Phương pháp:
Viết 9 dưới dạng lũy thừa cơ số 3, từ đó suy ra \(x.\)
Lời giải:
\(\begin{array}{l}{3^x} = 9\\{3^x} = {3^2}\\\,\,x = 2\end{array}\)
Đáp án C.
Câu 4. Giá trị của \(x\) thỏa mãn \(32:\left( {x - 32} \right) + 4 = 20\) là:
A. \(x = 16\)
B. \(x = 34\)
C. \(x = 32\)
D. \(x = 2\)
Phương pháp:
Áp dụng các quy tắc thực hiện phép tính.
Lời giải:
\(\begin{array}{l}32:\left( {x - 32} \right) + 4 = 20\\32:\left( {x - 32} \right)\,\,\,\,\,\,\,\,\, = 20 - 4\\32:\left( {x - 32} \right)\,\,\,\,\,\,\,\,\, = 16\\\,\,\,\,\,\,\,\,\,\,x - 32\,\,\,\,\,\,\,\,\,\,\, = 32:16\\\,\,\,\,\,\,\,\,\,\,x - 32\,\,\,\,\,\,\,\,\,\,\, = 2\\\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2 + 32\\\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 34\end{array}\)
Đáp án B.
Câu 5. Kết quả của phép tính \(17.25 + 23.25 + 25.60\) là:
A. 2500
B. 25
C. 250
D. 25000
Phương pháp:
Áp dụng tính chất phân phối của phép nhân và phép cộng:
\(a \cdot \left( {b + c} \right) = ab + ac\)
Lời giải:
\(\begin{array}{l}\,\,\,\,\,17.25 + 23.25 + 25.60\\ = 25.\left( {17 + 23 + 60} \right)\\ = 25.100\\ = 2500\end{array}\)
Đáp án A.
Câu 6. Đáp án khẳng định SAI trong các khẳng định sau:
A. \(4x\) chia hết cho 4
B. \(16 + 24\) chia hết cho 4
C. \(256 - 72\) chia hết cho 4
D. \(29 + 136\) chia hết cho 4
Phương pháp:
Áp dụng tính chất chia hết của một tổng, hiệu.
Lời giải:
Vì 136 chia hết cho 4 và 29 không chia hết cho 4 nên \(29 + 136\)không chia hết cho 4.
Đáp án D.
Câu 7. Số tự nhiên \(a,b\) thỏa mãn \(\overline {a5b} \) chia hết cho cho \(2;5;9\) là
A. \(a = 5;b = 0\)
B. \(a = 5;b = 5\)
C. \(a = 9;b = 4\)
D. \(a = 4;b = 0\)
Phương pháp:
Áp dụng dấu hiệu chia hết cho 2, 5, 9.
Lời giải:
\(\overline {a5b} \) chia hết cho 2 và 5 nên \(b = 0\)
\(\overline {a50} \) chia hết cho 9 nên \(a + 5 + 0 \vdots 9\) hay \(a + 5 \vdots 9 \Rightarrow a = 4\)
Vậy \(a = 4;\,b = 0.\)
Đáp án D.
Câu 8. Trong các số sau: \(123;256;448;250;513\) số chia hết cho 3 là:
A. \(123;513\)
B. \(256;448;250\)
C. 250
D. \(448;256\)
Phương pháp:
Sử dụng dấu hiệu chia hết cho 3.
Lời giải:
Các số chia hết cho 3 là: 123; 513.
Đáp án A.
Câu 9. Trong các hình dưới đây, hình nào là tam giác đều:

A. Hình a
B. Hình b
C. Hình c
D. Hình d
Phương pháp:
Dựa vào đặc điểm của tam giác đều.
Lời giải:
Hình c là tam giác đều.
Đáp án C.
Câu 10. Tổng số đường chéo của hình lục giác\(ABCDEF\)là:
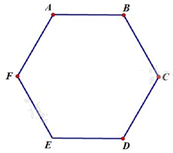
A. 8
B. 9
C. 10
D. 11
Phương pháp:
Số đường chéo của một hình đa giác n cạnh là: \(\frac{{n\left( {n - 3} \right)}}{2}.\)
Lời giải:
Đường chéo của hình lục giác \(ABCDEF\)là: \(\frac{{6.3}}{2} = 9.\)
Đáp án B.
Phần tự luận.
Bài 1.
a) Cho tập hợp \(A = \left\{ {1;2;3;5} \right\}\).
Điền kí hiệu \( \in , \notin \) thích hợp vào ô trống: $2 ... A; 4 ... A$
b) Tập hợp A bao gồm các số tự nhiên lớn hơn 8 và nhỏ hơn 12. Viết lại A theo 2 cách.
Phương pháp:
a) Xét xem phần tử 2 và 4 có thuộc tập A hay không, từ đó sử dụng kí hiệu thích hợp.
b) Viết tập hợp theo 2 cách:
Cách 1: Liệt kê các phần tử của tập hợp.
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Lời giải:
a) \({\rm{\;}}2 \in A{\rm{\;}} 4 \notin A\)
b) Tập A bao gồm các số tự nhiên lớn hơn 8 và nhỏ hơn 12.
\(\begin{array}{l}{\rm{C1:\;}}A = \left\{ {9;10;11} \right\}\\{\rm{C2:\;}}A = \{ x\mid x \in \mathbb{N}:8 < x < 12\} \end{array}\)
Bài 2. Thực hiện phép tính (tính hợp lí nếu có thể).
a) \(17 + 28 + 33 + 72\)
b) \({2^3}.17 - {2^3}.12\)
c) \(2022 - \left[ {2021 - {{(5 + 1)}^2}} \right] + {2023^0}\)
Phương pháp:
Áp dụng các quy tắc tính cộng, trừ, nhân, chia, lũy thừa.
Lời giải:
\(\begin{array}{*{20}{l}}{{\rm{a)\;}}\,17 + 28 + 33 + 72}\\{ = \left( {17 + 33} \right) + \left( {28 + 72} \right)}\\\begin{array}{l} = \,\,50 + 100\\ = 150\end{array}\end{array}\)
\(\begin{array}{*{20}{l}}{{\rm{b)\;}}\,{2^3}.17 - {2^3}.12}\\\begin{array}{l} = {2^3}.\left( {17 - 12} \right)\\ = {2^3}.5\\ = 8.5\\ = 40\end{array}\end{array}\)
\(\begin{array}{*{20}{r}}{{\rm{c}})}{2022 - \left[ {2021 - {{(5 + 1)}^2}} \right] + {{2023}^0}}\\ = {2022 - \left[ {2021 - {6^2}} \right] + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\ = {2022 - \left[ {2021 - 36} \right] + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\ = {2022 - 1985 + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\ = {37 + 1 = 38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}\)
Bài 3. Tìm số tự nhiên \(x\) biết
a) \(192 - x = 16\)
b) \(69 + \left( {x + 16} \right) = 185\)
c) \(\left[ {{{(x - 1)}^3} - {4^2}} \right] \cdot 3 = 327\)
Phương pháp:
Áp dụng các quy tắc thực hiện phép tính.
Lời giải:
\(\begin{array}{l}{\rm{a)}}\,\,192 - x = 16\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 192 - 16\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 176\end{array}\)
\(\begin{array}{l}{\rm{b}})\,\,69 + \left( {x + 16} \right) = 185\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x + 16\,\,\, = 185 - 69\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x + 16\,\,\, = 116\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\, = 116 - 16\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\, = 100\end{array}\)
\(\begin{array}{l}{\rm{c}})\,\left[ {{{(x - 1)}^3} - {4^2}} \right].3 = 327\\\,\,\,\,\,\,\,{(x - 1)^3} - 16\,\,\,\,\,\,\,\, = 327:3\\\,\,\,\,\,\,\,{(x - 1)^3} - 16\,\,\,\,\,\,\,\, = 109\\\,\,\,\,\,\,\,{(x - 1)^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 109 + 16\\\,\,\,\,\,\,\,{(x - 1)^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 125\\\,\,\,\,\,\,\,{(x - 1)^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {5^3}\\\,\,\,\,\,\,\,\,\,x - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 5\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 5 + 1\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 6\end{array}\)
Bài 4. Một căn phòng hình chữ nhật có chiều rộng 3 m, chiều dài 6 m. Tính chu vi và diện tích của căn phòng. Người ta lát nền nhà bằng các viên gạch hình vuông có chiều dài cạnh 30 cm. Biết giá tiền một viên gạch là 25 000 đồng. Hỏi để lát hết nền nhà cần bao nhiêu tiền?
Phương pháp:
Áp dụng công thức tính chu vi, diện tích hình chữ nhật.
\(\begin{array}{l}C = 2.\left( {a + b} \right)\\S = a.b\end{array}\)
Số viên gạch = Diện tích căn phòng : Diện tích viên gạch.
Số tiền lát nhà = Giá tiền 1 viên gạch × Số viên gạch.
Lời giải:
Chu vi căn phòng là: \(2.\left( {6 + 3} \right) = 18\left( {\rm{m}} \right)\)
Diện tích căn phòng là: \(6.3 = 18\left( {{{\rm{m}}^2}} \right)\)
Đổi \(18\,{{\rm{m}}^2} = 180\,000\,{\rm{c}}{{\rm{m}}^2}\)
Diện tích mỗi viên gạch là: \(30.30 = 900\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Số viên gạch cần dùng là: \(180\,000:900 = 200\) (viên)
Để lát hết nền nhà cần số tiền là: \(25\,000 \times 200 = 5\,000\,000\) (đồng)
Bài 5. Tìm số tự nhiên n để \(\left( {4n + 8} \right):\left( {3n + 2} \right)\left( {n \ge 1} \right)\).
Phương pháp:
Sử dụng tính chất chia hết của một tổng, hiệu.
Lời giải:
\(\left( {4n + 8} \right) \vdots \left( {3n + 2} \right)\,\,\left( {n \ge 1} \right)\)
Ta có: \(\left( {4n + 8} \right) \vdots \left( {3n + 2} \right) \Rightarrow 3\left( {4n + 8} \right) \vdots \left( {3n + 2} \right)\)
\(3(4n + 8) = 12n + 24 = 4(3n + 2) + 16\)
Để \(3(4n + 8) \vdots (3n + 2)\) thì \((12n + 24) \vdots (3n + 2)\)
\( \Rightarrow 4(3n + 2) + 16 \vdots (3n + 2)\) mà \(4(3n + 2) \vdots (3n + 2)\) nên \(16 \vdots (3n + 2)\)
Hay \((3n + 2)\)là ước của 16.
Ta có ước của 16 là: \(1;2;4;8;16.\)
Ta có bảng sau:
\(3n + 2\) | 1 | 2 | 4 | 8 | 16 |
\(3n\) | X | 0 | 2 | 6 | 14 |
\(n\) | X (loại) | 0 | X (loại) | 2 | X (loại) |
Vì \(n \ge 1\) nên \(n = 2\) là giá trị cần tìm.
Tải về
Phần trắc nghiệm
Câu 1. Tính chất nào KHÔNG phải là tính chất của phép nhân:
A. \(a \cdot b = b \cdot a\)
B. \(a \cdot \left( {b + c} \right) = ab + ac\)
C. \(a \cdot 1 = 1 \cdot a = a\)
D. \(a + 0 = 0 + a = a\)
Câu 2. Kết quả của phép tính \({5^3}:5\) là:
A. \({5^4}\)
B. \({5^3}\)
C. 25
D. 5
Câu 3. Số tự nhiên \(x\) thỏa mãn \({3^x} = 9\) là:
A. \(x = 4\)
B. \(x = 3\)
C. \(x = 2\)
D. \(x = 1\)
Câu 4. Giá trị của \(x\) thỏa mãn \(32:\left( {x - 32} \right) + 4 = 20\) là:
A. \(x = 16\)
B. \(x = 34\)
C. \(x = 32\)
D. \(x = 2\)
Câu 5. Kết quả của phép tính \(17.25 + 23.25 + 25.60\) là:
A. 2500
B. 25
C. 250
D. 25000
Câu 6. Chọn khẳng định SAI trong các khẳng định sau:
A. \(4x\) chia hết cho 4
B. \(16 + 24\) chia hết cho 4
C. \(256 - 72\) chia hết cho 4
D. \(29 + 136\) chia hết cho 4
Câu 7. Số tự nhiên \(a,b\) thỏa mãn \(\overline {a5b} \) chia hết cho cho \(2;5;9\) là
A. \(a = 5;b = 0\)
B. \(a = 5;b = 5\)
C. \(a = 9;b = 4\)
D. \(a = 4;b = 0\)
Câu 8. Trong các số sau: \(123;256;448;250;513\) số chia hết cho 3 là:
A. \(123;513\)
B. \(256;448;250\)
C. 250
D. \(448;256\)
Câu 9. Trong các hình dưới đây, hình nào là tam giác đều:

A. Hình a
B. Hình b
C. Hình c
D. Hình d
Câu 10. Tổng số đường chéo của hình lục giác\(ABCDEF\)là:
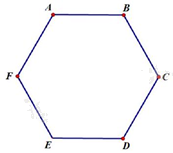
A. 8
B. 9
C. 10
D. 11
Phần tự luận
Bài 1.
a) Cho tập hợp \(A = \left\{ {1;2;3;5} \right\}\).
Điền kí hiệu \( \in , \notin \) thích hợp vào ô trống: $2 ... A; 4 ... A$
b) Tập hợp A bao gồm các số tự nhiên lớn hơn 8 và nhỏ hơn 12. Viết lại A theo 2 cách.
Bài 2. Thực hiện phép tính (tính hợp lí nếu có thể).
a) \(17 + 28 + 33 + 72\)
b) \({2^3}.17 - {2^3}.12\)
c) \(2022 - \left[ {2021 - {{(5 + 1)}^2}} \right] + {2023^0}\)
Bài 3. Tìm số tự nhiên \(x\) biết
a) \(192 - x = 16\)
b) \(69 + \left( {x + 16} \right) = 185\)
c) \(\left[ {{{(x - 1)}^3} - {4^2}} \right] \cdot 3 = 327\)
Bài 4. Một căn phòng hình chữ nhật có chiều rộng 3 m, chiều dài 6 m. Tính chu vi và diện tích của căn phòng. Người ta lát nền nhà bằng các viên gạch hình vuông có chiều dài cạnh 30 cm. Biết giá tiền một viên gạch là 25 000 đồng. Hỏi để lát hết nền nhà cần bao nhiêu tiền?
Bài 5. Tìm số tự nhiên n để \(\left( {4n + 8} \right):\left( {3n + 2} \right)\left( {n \ge 1} \right)\).
-------- Hết --------
Phần trắc nghiệm
1.D | 2.C | 3.C | 4.B | 5.A | 6.D | 7.D | 8.A | 9.C | 10.B |
Câu 1. Tính chất nào KHÔNG phải là tính chất của phép nhân:
A. \(a \cdot b = b \cdot a\)
B. \(a \cdot \left( {b + c} \right) = ab + ac\)
C. \(a \cdot 1 = 1 \cdot a = a\)
D. \(a + 0 = 0 + a = a\)
Phương pháp:
Nhận biết các tính chất cơ bản của phép nhân.
Lời giải:
\(a + 0 = 0 + a = a\) là tính chất của phép cộng, không phải phép nhân.
Đáp án D.
Câu 2. Kết quả của phép tính \({5^3}:5\) là:
A. \({5^4}\)
B. \({5^3}\)
C. 25
D. 5
Phương pháp:
Sử dụng công thức chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\)
Lời giải:
\({5^3}:5 = {5^2} = 25\)
Đáp án C.
Câu 3. Số tự nhiên \(x\) thỏa mãn \({3^x} = 9\) là:
A. \(x = 4\)
B. \(x = 3\)
C. \(x = 2\)
D. \(x = 1\)
Phương pháp:
Viết 9 dưới dạng lũy thừa cơ số 3, từ đó suy ra \(x.\)
Lời giải:
\(\begin{array}{l}{3^x} = 9\\{3^x} = {3^2}\\\,\,x = 2\end{array}\)
Đáp án C.
Câu 4. Giá trị của \(x\) thỏa mãn \(32:\left( {x - 32} \right) + 4 = 20\) là:
A. \(x = 16\)
B. \(x = 34\)
C. \(x = 32\)
D. \(x = 2\)
Phương pháp:
Áp dụng các quy tắc thực hiện phép tính.
Lời giải:
\(\begin{array}{l}32:\left( {x - 32} \right) + 4 = 20\\32:\left( {x - 32} \right)\,\,\,\,\,\,\,\,\, = 20 - 4\\32:\left( {x - 32} \right)\,\,\,\,\,\,\,\,\, = 16\\\,\,\,\,\,\,\,\,\,\,x - 32\,\,\,\,\,\,\,\,\,\,\, = 32:16\\\,\,\,\,\,\,\,\,\,\,x - 32\,\,\,\,\,\,\,\,\,\,\, = 2\\\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2 + 32\\\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 34\end{array}\)
Đáp án B.
Câu 5. Kết quả của phép tính \(17.25 + 23.25 + 25.60\) là:
A. 2500
B. 25
C. 250
D. 25000
Phương pháp:
Áp dụng tính chất phân phối của phép nhân và phép cộng:
\(a \cdot \left( {b + c} \right) = ab + ac\)
Lời giải:
\(\begin{array}{l}\,\,\,\,\,17.25 + 23.25 + 25.60\\ = 25.\left( {17 + 23 + 60} \right)\\ = 25.100\\ = 2500\end{array}\)
Đáp án A.
Câu 6. Đáp án khẳng định SAI trong các khẳng định sau:
A. \(4x\) chia hết cho 4
B. \(16 + 24\) chia hết cho 4
C. \(256 - 72\) chia hết cho 4
D. \(29 + 136\) chia hết cho 4
Phương pháp:
Áp dụng tính chất chia hết của một tổng, hiệu.
Lời giải:
Vì 136 chia hết cho 4 và 29 không chia hết cho 4 nên \(29 + 136\)không chia hết cho 4.
Đáp án D.
Câu 7. Số tự nhiên \(a,b\) thỏa mãn \(\overline {a5b} \) chia hết cho cho \(2;5;9\) là
A. \(a = 5;b = 0\)
B. \(a = 5;b = 5\)
C. \(a = 9;b = 4\)
D. \(a = 4;b = 0\)
Phương pháp:
Áp dụng dấu hiệu chia hết cho 2, 5, 9.
Lời giải:
\(\overline {a5b} \) chia hết cho 2 và 5 nên \(b = 0\)
\(\overline {a50} \) chia hết cho 9 nên \(a + 5 + 0 \vdots 9\) hay \(a + 5 \vdots 9 \Rightarrow a = 4\)
Vậy \(a = 4;\,b = 0.\)
Đáp án D.
Câu 8. Trong các số sau: \(123;256;448;250;513\) số chia hết cho 3 là:
A. \(123;513\)
B. \(256;448;250\)
C. 250
D. \(448;256\)
Phương pháp:
Sử dụng dấu hiệu chia hết cho 3.
Lời giải:
Các số chia hết cho 3 là: 123; 513.
Đáp án A.
Câu 9. Trong các hình dưới đây, hình nào là tam giác đều:

A. Hình a
B. Hình b
C. Hình c
D. Hình d
Phương pháp:
Dựa vào đặc điểm của tam giác đều.
Lời giải:
Hình c là tam giác đều.
Đáp án C.
Câu 10. Tổng số đường chéo của hình lục giác\(ABCDEF\)là:
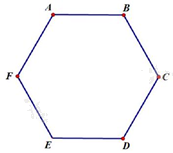
A. 8
B. 9
C. 10
D. 11
Phương pháp:
Số đường chéo của một hình đa giác n cạnh là: \(\frac{{n\left( {n - 3} \right)}}{2}.\)
Lời giải:
Đường chéo của hình lục giác \(ABCDEF\)là: \(\frac{{6.3}}{2} = 9.\)
Đáp án B.
Phần tự luận.
Bài 1.
a) Cho tập hợp \(A = \left\{ {1;2;3;5} \right\}\).
Điền kí hiệu \( \in , \notin \) thích hợp vào ô trống: $2 ... A; 4 ... A$
b) Tập hợp A bao gồm các số tự nhiên lớn hơn 8 và nhỏ hơn 12. Viết lại A theo 2 cách.
Phương pháp:
a) Xét xem phần tử 2 và 4 có thuộc tập A hay không, từ đó sử dụng kí hiệu thích hợp.
b) Viết tập hợp theo 2 cách:
Cách 1: Liệt kê các phần tử của tập hợp.
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Lời giải:
a) \({\rm{\;}}2 \in A{\rm{\;}} 4 \notin A\)
b) Tập A bao gồm các số tự nhiên lớn hơn 8 và nhỏ hơn 12.
\(\begin{array}{l}{\rm{C1:\;}}A = \left\{ {9;10;11} \right\}\\{\rm{C2:\;}}A = \{ x\mid x \in \mathbb{N}:8 < x < 12\} \end{array}\)
Bài 2. Thực hiện phép tính (tính hợp lí nếu có thể).
a) \(17 + 28 + 33 + 72\)
b) \({2^3}.17 - {2^3}.12\)
c) \(2022 - \left[ {2021 - {{(5 + 1)}^2}} \right] + {2023^0}\)
Phương pháp:
Áp dụng các quy tắc tính cộng, trừ, nhân, chia, lũy thừa.
Lời giải:
\(\begin{array}{*{20}{l}}{{\rm{a)\;}}\,17 + 28 + 33 + 72}\\{ = \left( {17 + 33} \right) + \left( {28 + 72} \right)}\\\begin{array}{l} = \,\,50 + 100\\ = 150\end{array}\end{array}\)
\(\begin{array}{*{20}{l}}{{\rm{b)\;}}\,{2^3}.17 - {2^3}.12}\\\begin{array}{l} = {2^3}.\left( {17 - 12} \right)\\ = {2^3}.5\\ = 8.5\\ = 40\end{array}\end{array}\)
\(\begin{array}{*{20}{r}}{{\rm{c}})}{2022 - \left[ {2021 - {{(5 + 1)}^2}} \right] + {{2023}^0}}\\ = {2022 - \left[ {2021 - {6^2}} \right] + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\ = {2022 - \left[ {2021 - 36} \right] + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\ = {2022 - 1985 + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\ = {37 + 1 = 38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}\)
Bài 3. Tìm số tự nhiên \(x\) biết
a) \(192 - x = 16\)
b) \(69 + \left( {x + 16} \right) = 185\)
c) \(\left[ {{{(x - 1)}^3} - {4^2}} \right] \cdot 3 = 327\)
Phương pháp:
Áp dụng các quy tắc thực hiện phép tính.
Lời giải:
\(\begin{array}{l}{\rm{a)}}\,\,192 - x = 16\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 192 - 16\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 176\end{array}\)
\(\begin{array}{l}{\rm{b}})\,\,69 + \left( {x + 16} \right) = 185\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x + 16\,\,\, = 185 - 69\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x + 16\,\,\, = 116\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\, = 116 - 16\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\, = 100\end{array}\)
\(\begin{array}{l}{\rm{c}})\,\left[ {{{(x - 1)}^3} - {4^2}} \right].3 = 327\\\,\,\,\,\,\,\,{(x - 1)^3} - 16\,\,\,\,\,\,\,\, = 327:3\\\,\,\,\,\,\,\,{(x - 1)^3} - 16\,\,\,\,\,\,\,\, = 109\\\,\,\,\,\,\,\,{(x - 1)^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 109 + 16\\\,\,\,\,\,\,\,{(x - 1)^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 125\\\,\,\,\,\,\,\,{(x - 1)^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {5^3}\\\,\,\,\,\,\,\,\,\,x - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 5\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 5 + 1\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 6\end{array}\)
Bài 4. Một căn phòng hình chữ nhật có chiều rộng 3 m, chiều dài 6 m. Tính chu vi và diện tích của căn phòng. Người ta lát nền nhà bằng các viên gạch hình vuông có chiều dài cạnh 30 cm. Biết giá tiền một viên gạch là 25 000 đồng. Hỏi để lát hết nền nhà cần bao nhiêu tiền?
Phương pháp:
Áp dụng công thức tính chu vi, diện tích hình chữ nhật.
\(\begin{array}{l}C = 2.\left( {a + b} \right)\\S = a.b\end{array}\)
Số viên gạch = Diện tích căn phòng : Diện tích viên gạch.
Số tiền lát nhà = Giá tiền 1 viên gạch × Số viên gạch.
Lời giải:
Chu vi căn phòng là: \(2.\left( {6 + 3} \right) = 18\left( {\rm{m}} \right)\)
Diện tích căn phòng là: \(6.3 = 18\left( {{{\rm{m}}^2}} \right)\)
Đổi \(18\,{{\rm{m}}^2} = 180\,000\,{\rm{c}}{{\rm{m}}^2}\)
Diện tích mỗi viên gạch là: \(30.30 = 900\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Số viên gạch cần dùng là: \(180\,000:900 = 200\) (viên)
Để lát hết nền nhà cần số tiền là: \(25\,000 \times 200 = 5\,000\,000\) (đồng)
Bài 5. Tìm số tự nhiên n để \(\left( {4n + 8} \right):\left( {3n + 2} \right)\left( {n \ge 1} \right)\).
Phương pháp:
Sử dụng tính chất chia hết của một tổng, hiệu.
Lời giải:
\(\left( {4n + 8} \right) \vdots \left( {3n + 2} \right)\,\,\left( {n \ge 1} \right)\)
Ta có: \(\left( {4n + 8} \right) \vdots \left( {3n + 2} \right) \Rightarrow 3\left( {4n + 8} \right) \vdots \left( {3n + 2} \right)\)
\(3(4n + 8) = 12n + 24 = 4(3n + 2) + 16\)
Để \(3(4n + 8) \vdots (3n + 2)\) thì \((12n + 24) \vdots (3n + 2)\)
\( \Rightarrow 4(3n + 2) + 16 \vdots (3n + 2)\) mà \(4(3n + 2) \vdots (3n + 2)\) nên \(16 \vdots (3n + 2)\)
Hay \((3n + 2)\)là ước của 16.
Ta có ước của 16 là: \(1;2;4;8;16.\)
Ta có bảng sau:
\(3n + 2\) | 1 | 2 | 4 | 8 | 16 |
\(3n\) | X | 0 | 2 | 6 | 14 |
\(n\) | X (loại) | 0 | X (loại) | 2 | X (loại) |
Vì \(n \ge 1\) nên \(n = 2\) là giá trị cần tìm.
Đề thi giữa kì 1 Toán 6 - Đề số 12 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kỳ đầu tiên. Đề thi thường bao gồm các chủ đề chính như số tự nhiên, tập hợp, phép tính trên số tự nhiên, ước và bội, và các bài toán thực tế liên quan.
Cấu trúc đề thi có thể khác nhau tùy theo từng trường và giáo viên, nhưng thường bao gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 1 Toán 6 - Đề số 12:
Các bài tập liên quan đến số tự nhiên thường yêu cầu học sinh:
Các bài tập về phép tính trên số tự nhiên yêu cầu học sinh:
Các bài tập về ước và bội yêu cầu học sinh:
Các bài toán thực tế thường yêu cầu học sinh:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 6, học sinh cần:
Ngoài việc giải đề thi, học sinh có thể tham khảo các tài liệu ôn tập sau:
Hãy dành thời gian ôn tập và luyện tập một cách nghiêm túc. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 6!