Chào mừng các em học sinh đến với đề thi học kì 2 môn Toán lớp 6 - Đề số 2, chương trình Kết nối tri thức. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi với cấu trúc tương tự đề thi chính thức, kèm theo đáp án chi tiết và lời giải dễ hiểu. Hãy cùng thử sức để đạt kết quả tốt nhất nhé!
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho 6 điểm trong đó không có ba điểm nào thẳng hàng. Qua hai điểm vẽ được một đường thẳng. Số đường thẳng vẽ được là:
A. 10
B. 18
C. 12
D. 15
Câu 2:Viết tên góc ở hình vẽ bên bằng kí hiệu.
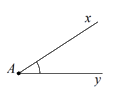
A. \(\angle Axy\)
B. \(\angle xyA\)
C. \(\angle xAy\)
D. \(\angle xy\)
Câu 3: Bạn Hòa đi siêu thị mua thực phẩm tổng hết 500 nghìn đồng. Ngày hôm đó siêu thị giảm giá 20%. Số tiền Hòa phải trả nếu không được giảm là:
A. 600 nghìn đồng
B. 625 nghìn đồng
C. 450 nghìn đồng
D. 400 nghìn đồng
Câu 4:Gieo một con xúc xắc sáu mặt 13 lần liên tiếp, có 7 lần xuất hiện mặt hai chấm thì xác suất thực nghiệm xuất hiện mặt hai chấm là:
A. \(\dfrac{7}{{13}}\)
B. \(\dfrac{2}{7}\)
C. \(\dfrac{2}{{13}}\)
D. \(\dfrac{9}{{13}}\)
Phần II. Tự luận (8 điểm):
Bài 1: (1.5 điểm) Thực hiện các phép tính:
\(a)\,\dfrac{{31}}{{17}} + \dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}} - \dfrac{{14}}{{17}}\)
\(b)\,7\dfrac{5}{{11}} - \left( {2\dfrac{3}{7} + 3\dfrac{5}{{11}}} \right)\)
Bài 2:(2 điểm)Tìm x biết:
a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\)
b) \(3 \cdot {\left( {3x - \dfrac{1}{2}} \right)^3} + \dfrac{1}{9} = 0\)
c) \(12,3:x - 4,5:x = 15\)
d) \(\dfrac{{3 - x}}{{5 - x}} = {\left( {\dfrac{{ - 3}}{5}} \right)^2}\)
Bài 3 (1,5 điểm) Một lớp học có 50 học sinh gồm: giỏi, khá, trung bình. Số học sinh trung bình chiếm \(\dfrac{3}{{10}}\) số học sinh cả lớp. Số học sinh khá bằng \(40\% \) số học sinh còn lại.
a) Tính số học sinh mỗi loại của lớp đó.
b) Tính tỉ số phần trăm của học sinh giỏi so với số học sinh cả lớp.
Bài 4: (2,5 điểm) Trên tia An lấy 2 điểm K và Q sao cho AK = 3cm, AQ = 4cm.
a) Tính độ dài đoạn thẳng KQ.
b) Lấy điểm C trên tia Am là tia đối của tia An sao cho AC = 3cm, tính CK.
Điểm A có là trung điểm của đoạn thẳng CK không? Vì sao?
c) Lấy điểm B là trung điểm của đoạn thẳng CA. So sánh BK và AQ?
Bài 5:(0,5 điểm)Tìm các số nguyên n để biểu thức sau nhận giá trị là số nguyên: \(A = \dfrac{{3n - 4}}{{2 - n}}\).
Phần I: Trắc nghiệm
1. D | 2. C | 3. B | 4. A |
Câu 1
Phương pháp:
Cứ qua 2 điểm ta vẽ 1 đường thẳng nên với \(n\) điểm không thẳng hàng có tất cả: \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) (đường thẳng)
Cách giải:
Qua 6 điểm trong đó không có 3 điểm nào thẳng hàng ta vẽ được: \(\dfrac{{6.5}}{2} = 15\) (đường thẳng)
Chọn D.
Câu 2
Phương pháp:
Hai tia Ox, Oy phân biệt tạo thành góc \(\angle xOy\).
Cách giải:
Góc đã cho được kí hiệu là \(\angle xAy\).
Chọn C.
Câu 3
Phương pháp:
Sau khi được giảm 20%, số tiền phải trả bằng 80% số tiền ban đầu. Ta lấy số hết Hòa đã trả chia 80%.
Cách giải:
Số tiền Hòa phải trả là: \(500:\dfrac{{100 - 20}}{{100}} = 625\)(nghìn đồng)
Chọn B.
Câu 4
Phương pháp
Xác suất thực nghiệm xuất hiện mặt i chấm khi tung xúc xắc nhiều lần là: Số lần xuất hiện mặt i chấm : Tổng số lần tung xúc xắc.
Cách giải:
Xác suất thực nghiệm xuất hiện mặt hai chấm khi tung xúc xắc nhiều lần là: \(\dfrac{7}{{13}}\).
Chọn A.
Phần II: Tự luận
Bài 1
Phương pháp
a) Nhóm các số hạng có cùng mẫu số, rồi thực hiện cộng trừ các phân số có cùng mẫu số.
b) Tách hỗn số thành hai phần: phần nguyên và phần phân số, rồi cộng phần nguyên với nhau, cộng phần phân số với nhau.
Chú ý: Muốn cộng (trừ) hai phân số có cùng mẫu số, ta cộng (trừ) tử số với nhau và giữ nguyên mẫu số.
Cách giải:
\(a)\,\dfrac{{31}}{{17}} + \dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}} - \dfrac{{14}}{{17}} = \left( {\dfrac{{31}}{{17}} - \dfrac{{14}}{{17}}} \right) + \left( {\dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}}} \right) = \dfrac{{17}}{{17}} + \dfrac{{ - 13}}{{13}} = 1 + \left( { - 1} \right)\, = 0\)
\(\begin{array}{l}b)\,7\dfrac{5}{{11}} - \left( {2\dfrac{3}{7} + 3\dfrac{5}{{11}}} \right) = 7 + \dfrac{5}{{11}} - \left( {2 + \dfrac{3}{7} + 3 + \dfrac{5}{{11}}} \right) = 7 + \dfrac{5}{{11}} - 2 - 3 - \dfrac{3}{7} - \dfrac{5}{{11}}\\\, = \left( {7 - 2 - 3} \right) + \left( {\dfrac{5}{{11}} - \dfrac{5}{{11}}} \right) - \dfrac{3}{7} = 2 + 0 - \dfrac{3}{7}\, = \dfrac{{11}}{7}\end{array}\)
Bài 2
Phương pháp
Áp dụng các kiến thức:
- Sử dụng các công thức lũy thừa và quy tắc bỏ ngoặc để tìm x
- Áp dụng quy tắc chuyển vế đổi dấu x.
- Đặt điều kiện để các phân số có nghĩa, tìm x.
Chú ý sau khi tìm được \(x\) cần đối chiếu với điều kiện rồi kết luận \(x\)
Cách giải:
a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\)
\(\begin{array}{l}\dfrac{1}{3}x + \dfrac{2}{5}x - \dfrac{2}{5} = 0\\\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right)x = \dfrac{2}{5}\\\dfrac{{11}}{{15}}x = \dfrac{2}{5}\end{array}\)
\(x = \dfrac{2}{5}:\dfrac{{11}}{{15}}\)
\(\begin{array}{l}x = \dfrac{2}{5} \cdot \dfrac{{15}}{{11}}\\x = \dfrac{6}{{11}}\end{array}\)
Vậy \(x = \dfrac{6}{{11}} \cdot \)
b) \(3.{\left( {3x - \dfrac{1}{2}} \right)^3} + \dfrac{1}{9} = 0\)
\(\begin{array}{l}3.{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{9}\\{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{9}:3\\{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{{27}} = \left( {\dfrac{{ - 1}}{3}} \right)\end{array}\)
\( \Rightarrow 3x - \dfrac{1}{2} = {\dfrac{{ - 1}}{3}^3}\)
\(\begin{array}{l}3x = \dfrac{{ - 1}}{3} + \dfrac{1}{2}\\3x = \dfrac{{ - 2}}{6} + \dfrac{3}{6}\\3x = \dfrac{1}{6}\\x = \dfrac{1}{{18}}\end{array}\)
Vậy \(x = \dfrac{1}{{18}} \cdot \)
c) \(12,3:x - 4,5:x = 15\)
\(\begin{array}{l}\left( {12,3 - 4,5} \right):x = 15\\7,8:x = 15\\x = 7,8:15\\x = 0,52\end{array}\)
Vậy \(x = 0,52\)
d) \(\dfrac{{3 - x}}{{5 - x}} = {\left( {\dfrac{{ - 3}}{5}} \right)^2}\)
Điều kiện: \(5 - x \ne 0 \Leftrightarrow x \ne 5.\)
\(\begin{array}{*{20}{l}}{ \Rightarrow \dfrac{{3 - x}}{{5 - x}} = \dfrac{9}{{25}}}\\{ \Rightarrow \left( {3 - x} \right).25 = 9.\left( {5 - x} \right)}\\{75 - 25x = 45 - 9x}\\{ - 25x + 9x = 45 - 75}\\{ - 16x = {\rm{ \;}} - 30}\\{x = \dfrac{{ - 30}}{{ - 16}} = \dfrac{{15}}{8}}\end{array}\)
Vậy \(x = \dfrac{{15}}{8} \cdot \)
Bài 3
Phương pháp:
a) Áp dụng quy tắc: Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\left( {m,n \in \mathbb{N},n \ne 0} \right).\)
b) Áp dụng quy tắc tìm tỉ số phần trăm của hai số : Muốn tìm tỉ số phần trăm của hai số \(a\) và \(b\), ta nhân \(a\) với 100 rồi chia cho \(b\) và viết kí hiệu \(\% \) vào kết quả : \(\dfrac{{a.100}}{b}\% \).
Cách giải:
a) Lớp học đó có số học sinh trung bình là :
\(50.\dfrac{3}{{10}} = 15\) (học sinh)
Lớp đó có số học sinh giỏi và khá là :
\(50 - 15 = 35\) (học sinh)
Lớp đó có số học sinh khá là :
\(35.40\% {\rm{\;}} = 14\) (học sinh)
Lớp đó có số học sinh giỏi là :
\(35 - 14 = 21\) (học sinh)
b) Tỉ số phần trăm của học sinh giỏi so với số học sinh cả lớp là:
\(21:50.100\% {\rm{\;}} = 42\% \)
Bài 4
Phương pháp
a) Chứng minh K nằm giữa A và Q và suy ra AK + KQ = AQ.
b) Chứng minh A nằm giữa C và K. Tính CK = AC + AK.
Chỉ ra A nằm giữa C, K và AC = AK. Từ đó suy ra A là trung điểm của CK.
c) Tính BA.
Chứng minh A nằm giữa B và K. Tính BK = BA + AK.
So sánh BK và AQ.
Cách giải:
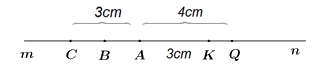
a) Vì AK < AQ (3cm < 4cm) nên K nằm giữa A và Q.
=> AK + KQ = AQ
=> 3 + KQ = 4
=> KQ = 4 – 3
=> KQ = 1 (cm)
b) Vì C và K nằm trên hai tia đối An và Am nên A nằm giữa C và K.
=> CK = AC + AK
=> CK = 3 + 3
=> CK = 6 (cm)
Ta có: A nằm giữa C và K.
AC = AK = 3cm.
=> A là trung điểm của CK.
c) Vì B là trung điểm của AC nên BA = AC : 2 = 3 : 2 = 1,5 (cm).
Vì B, K nằm trên hai tia đối nhau An và Am nên A nằm giữa B và K.
=> BK = BA + AK
=> BK = 1,5 + 3
=> BK = 4,5 (cm)
Mà AQ = 4 (cm)
=> BK > AQ.
Bài 5
Phương pháp
Phân tích \(A = a + \dfrac{b}{{2 - n}}\), với \(a,\,\,b \in \mathbb{Z}\).
Để \(A \in \mathbb{Z}\) thì \(2 - n \in U\left( b \right)\).
Cách giải:
\(\begin{array}{l}A = \dfrac{{3n - 4}}{{2 - n}} = \dfrac{{3n - 6 + 2}}{{ - n + 2}}\\\,\,\,\,\, = \dfrac{{3n - 6}}{{ - n + 2}} + \dfrac{2}{{ - n + 2}}\\\,\,\,\,\, = \dfrac{{ - 3\left( { - n + 2} \right)}}{{ - n + 2}} + \dfrac{2}{{ - n + 2}}\\\,\,\,\,\, = - 3 + \dfrac{2}{{ - n + 2}}\end{array}\)
Để A nhận giá trị nguyên thì \( - 3 + \dfrac{2}{{ - n + 2}} \in \mathbb{Z} \Rightarrow \dfrac{2}{{ - n + 2}} \in \mathbb{Z}\)\( \Rightarrow - n + 2 \in \left\{ { \pm 1; \pm 2} \right\}\)
Ta có bảng giá trị sau:
\( - n + 2\) | 1 | -1 | 2 | -2 |
\(n\) | 1 (TM) | 3 (TM) | 0 (TM) | 4 (TM) |
Vậy \(n \in \left\{ {1;3;0;4} \right\}\).
Tải về
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho 6 điểm trong đó không có ba điểm nào thẳng hàng. Qua hai điểm vẽ được một đường thẳng. Số đường thẳng vẽ được là:
A. 10
B. 18
C. 12
D. 15
Câu 2:Viết tên góc ở hình vẽ bên bằng kí hiệu.
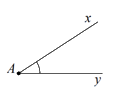
A. \(\angle Axy\)
B. \(\angle xyA\)
C. \(\angle xAy\)
D. \(\angle xy\)
Câu 3: Bạn Hòa đi siêu thị mua thực phẩm tổng hết 500 nghìn đồng. Ngày hôm đó siêu thị giảm giá 20%. Số tiền Hòa phải trả nếu không được giảm là:
A. 600 nghìn đồng
B. 625 nghìn đồng
C. 450 nghìn đồng
D. 400 nghìn đồng
Câu 4:Gieo một con xúc xắc sáu mặt 13 lần liên tiếp, có 7 lần xuất hiện mặt hai chấm thì xác suất thực nghiệm xuất hiện mặt hai chấm là:
A. \(\dfrac{7}{{13}}\)
B. \(\dfrac{2}{7}\)
C. \(\dfrac{2}{{13}}\)
D. \(\dfrac{9}{{13}}\)
Phần II. Tự luận (8 điểm):
Bài 1: (1.5 điểm) Thực hiện các phép tính:
\(a)\,\dfrac{{31}}{{17}} + \dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}} - \dfrac{{14}}{{17}}\)
\(b)\,7\dfrac{5}{{11}} - \left( {2\dfrac{3}{7} + 3\dfrac{5}{{11}}} \right)\)
Bài 2:(2 điểm)Tìm x biết:
a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\)
b) \(3 \cdot {\left( {3x - \dfrac{1}{2}} \right)^3} + \dfrac{1}{9} = 0\)
c) \(12,3:x - 4,5:x = 15\)
d) \(\dfrac{{3 - x}}{{5 - x}} = {\left( {\dfrac{{ - 3}}{5}} \right)^2}\)
Bài 3 (1,5 điểm) Một lớp học có 50 học sinh gồm: giỏi, khá, trung bình. Số học sinh trung bình chiếm \(\dfrac{3}{{10}}\) số học sinh cả lớp. Số học sinh khá bằng \(40\% \) số học sinh còn lại.
a) Tính số học sinh mỗi loại của lớp đó.
b) Tính tỉ số phần trăm của học sinh giỏi so với số học sinh cả lớp.
Bài 4: (2,5 điểm) Trên tia An lấy 2 điểm K và Q sao cho AK = 3cm, AQ = 4cm.
a) Tính độ dài đoạn thẳng KQ.
b) Lấy điểm C trên tia Am là tia đối của tia An sao cho AC = 3cm, tính CK.
Điểm A có là trung điểm của đoạn thẳng CK không? Vì sao?
c) Lấy điểm B là trung điểm của đoạn thẳng CA. So sánh BK và AQ?
Bài 5:(0,5 điểm)Tìm các số nguyên n để biểu thức sau nhận giá trị là số nguyên: \(A = \dfrac{{3n - 4}}{{2 - n}}\).
Phần I: Trắc nghiệm
1. D | 2. C | 3. B | 4. A |
Câu 1
Phương pháp:
Cứ qua 2 điểm ta vẽ 1 đường thẳng nên với \(n\) điểm không thẳng hàng có tất cả: \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) (đường thẳng)
Cách giải:
Qua 6 điểm trong đó không có 3 điểm nào thẳng hàng ta vẽ được: \(\dfrac{{6.5}}{2} = 15\) (đường thẳng)
Chọn D.
Câu 2
Phương pháp:
Hai tia Ox, Oy phân biệt tạo thành góc \(\angle xOy\).
Cách giải:
Góc đã cho được kí hiệu là \(\angle xAy\).
Chọn C.
Câu 3
Phương pháp:
Sau khi được giảm 20%, số tiền phải trả bằng 80% số tiền ban đầu. Ta lấy số hết Hòa đã trả chia 80%.
Cách giải:
Số tiền Hòa phải trả là: \(500:\dfrac{{100 - 20}}{{100}} = 625\)(nghìn đồng)
Chọn B.
Câu 4
Phương pháp
Xác suất thực nghiệm xuất hiện mặt i chấm khi tung xúc xắc nhiều lần là: Số lần xuất hiện mặt i chấm : Tổng số lần tung xúc xắc.
Cách giải:
Xác suất thực nghiệm xuất hiện mặt hai chấm khi tung xúc xắc nhiều lần là: \(\dfrac{7}{{13}}\).
Chọn A.
Phần II: Tự luận
Bài 1
Phương pháp
a) Nhóm các số hạng có cùng mẫu số, rồi thực hiện cộng trừ các phân số có cùng mẫu số.
b) Tách hỗn số thành hai phần: phần nguyên và phần phân số, rồi cộng phần nguyên với nhau, cộng phần phân số với nhau.
Chú ý: Muốn cộng (trừ) hai phân số có cùng mẫu số, ta cộng (trừ) tử số với nhau và giữ nguyên mẫu số.
Cách giải:
\(a)\,\dfrac{{31}}{{17}} + \dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}} - \dfrac{{14}}{{17}} = \left( {\dfrac{{31}}{{17}} - \dfrac{{14}}{{17}}} \right) + \left( {\dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}}} \right) = \dfrac{{17}}{{17}} + \dfrac{{ - 13}}{{13}} = 1 + \left( { - 1} \right)\, = 0\)
\(\begin{array}{l}b)\,7\dfrac{5}{{11}} - \left( {2\dfrac{3}{7} + 3\dfrac{5}{{11}}} \right) = 7 + \dfrac{5}{{11}} - \left( {2 + \dfrac{3}{7} + 3 + \dfrac{5}{{11}}} \right) = 7 + \dfrac{5}{{11}} - 2 - 3 - \dfrac{3}{7} - \dfrac{5}{{11}}\\\, = \left( {7 - 2 - 3} \right) + \left( {\dfrac{5}{{11}} - \dfrac{5}{{11}}} \right) - \dfrac{3}{7} = 2 + 0 - \dfrac{3}{7}\, = \dfrac{{11}}{7}\end{array}\)
Bài 2
Phương pháp
Áp dụng các kiến thức:
- Sử dụng các công thức lũy thừa và quy tắc bỏ ngoặc để tìm x
- Áp dụng quy tắc chuyển vế đổi dấu x.
- Đặt điều kiện để các phân số có nghĩa, tìm x.
Chú ý sau khi tìm được \(x\) cần đối chiếu với điều kiện rồi kết luận \(x\)
Cách giải:
a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\)
\(\begin{array}{l}\dfrac{1}{3}x + \dfrac{2}{5}x - \dfrac{2}{5} = 0\\\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right)x = \dfrac{2}{5}\\\dfrac{{11}}{{15}}x = \dfrac{2}{5}\end{array}\)
\(x = \dfrac{2}{5}:\dfrac{{11}}{{15}}\)
\(\begin{array}{l}x = \dfrac{2}{5} \cdot \dfrac{{15}}{{11}}\\x = \dfrac{6}{{11}}\end{array}\)
Vậy \(x = \dfrac{6}{{11}} \cdot \)
b) \(3.{\left( {3x - \dfrac{1}{2}} \right)^3} + \dfrac{1}{9} = 0\)
\(\begin{array}{l}3.{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{9}\\{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{9}:3\\{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{{27}} = \left( {\dfrac{{ - 1}}{3}} \right)\end{array}\)
\( \Rightarrow 3x - \dfrac{1}{2} = {\dfrac{{ - 1}}{3}^3}\)
\(\begin{array}{l}3x = \dfrac{{ - 1}}{3} + \dfrac{1}{2}\\3x = \dfrac{{ - 2}}{6} + \dfrac{3}{6}\\3x = \dfrac{1}{6}\\x = \dfrac{1}{{18}}\end{array}\)
Vậy \(x = \dfrac{1}{{18}} \cdot \)
c) \(12,3:x - 4,5:x = 15\)
\(\begin{array}{l}\left( {12,3 - 4,5} \right):x = 15\\7,8:x = 15\\x = 7,8:15\\x = 0,52\end{array}\)
Vậy \(x = 0,52\)
d) \(\dfrac{{3 - x}}{{5 - x}} = {\left( {\dfrac{{ - 3}}{5}} \right)^2}\)
Điều kiện: \(5 - x \ne 0 \Leftrightarrow x \ne 5.\)
\(\begin{array}{*{20}{l}}{ \Rightarrow \dfrac{{3 - x}}{{5 - x}} = \dfrac{9}{{25}}}\\{ \Rightarrow \left( {3 - x} \right).25 = 9.\left( {5 - x} \right)}\\{75 - 25x = 45 - 9x}\\{ - 25x + 9x = 45 - 75}\\{ - 16x = {\rm{ \;}} - 30}\\{x = \dfrac{{ - 30}}{{ - 16}} = \dfrac{{15}}{8}}\end{array}\)
Vậy \(x = \dfrac{{15}}{8} \cdot \)
Bài 3
Phương pháp:
a) Áp dụng quy tắc: Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\left( {m,n \in \mathbb{N},n \ne 0} \right).\)
b) Áp dụng quy tắc tìm tỉ số phần trăm của hai số : Muốn tìm tỉ số phần trăm của hai số \(a\) và \(b\), ta nhân \(a\) với 100 rồi chia cho \(b\) và viết kí hiệu \(\% \) vào kết quả : \(\dfrac{{a.100}}{b}\% \).
Cách giải:
a) Lớp học đó có số học sinh trung bình là :
\(50.\dfrac{3}{{10}} = 15\) (học sinh)
Lớp đó có số học sinh giỏi và khá là :
\(50 - 15 = 35\) (học sinh)
Lớp đó có số học sinh khá là :
\(35.40\% {\rm{\;}} = 14\) (học sinh)
Lớp đó có số học sinh giỏi là :
\(35 - 14 = 21\) (học sinh)
b) Tỉ số phần trăm của học sinh giỏi so với số học sinh cả lớp là:
\(21:50.100\% {\rm{\;}} = 42\% \)
Bài 4
Phương pháp
a) Chứng minh K nằm giữa A và Q và suy ra AK + KQ = AQ.
b) Chứng minh A nằm giữa C và K. Tính CK = AC + AK.
Chỉ ra A nằm giữa C, K và AC = AK. Từ đó suy ra A là trung điểm của CK.
c) Tính BA.
Chứng minh A nằm giữa B và K. Tính BK = BA + AK.
So sánh BK và AQ.
Cách giải:
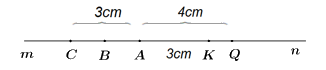
a) Vì AK < AQ (3cm < 4cm) nên K nằm giữa A và Q.
=> AK + KQ = AQ
=> 3 + KQ = 4
=> KQ = 4 – 3
=> KQ = 1 (cm)
b) Vì C và K nằm trên hai tia đối An và Am nên A nằm giữa C và K.
=> CK = AC + AK
=> CK = 3 + 3
=> CK = 6 (cm)
Ta có: A nằm giữa C và K.
AC = AK = 3cm.
=> A là trung điểm của CK.
c) Vì B là trung điểm của AC nên BA = AC : 2 = 3 : 2 = 1,5 (cm).
Vì B, K nằm trên hai tia đối nhau An và Am nên A nằm giữa B và K.
=> BK = BA + AK
=> BK = 1,5 + 3
=> BK = 4,5 (cm)
Mà AQ = 4 (cm)
=> BK > AQ.
Bài 5
Phương pháp
Phân tích \(A = a + \dfrac{b}{{2 - n}}\), với \(a,\,\,b \in \mathbb{Z}\).
Để \(A \in \mathbb{Z}\) thì \(2 - n \in U\left( b \right)\).
Cách giải:
\(\begin{array}{l}A = \dfrac{{3n - 4}}{{2 - n}} = \dfrac{{3n - 6 + 2}}{{ - n + 2}}\\\,\,\,\,\, = \dfrac{{3n - 6}}{{ - n + 2}} + \dfrac{2}{{ - n + 2}}\\\,\,\,\,\, = \dfrac{{ - 3\left( { - n + 2} \right)}}{{ - n + 2}} + \dfrac{2}{{ - n + 2}}\\\,\,\,\,\, = - 3 + \dfrac{2}{{ - n + 2}}\end{array}\)
Để A nhận giá trị nguyên thì \( - 3 + \dfrac{2}{{ - n + 2}} \in \mathbb{Z} \Rightarrow \dfrac{2}{{ - n + 2}} \in \mathbb{Z}\)\( \Rightarrow - n + 2 \in \left\{ { \pm 1; \pm 2} \right\}\)
Ta có bảng giá trị sau:
\( - n + 2\) | 1 | -1 | 2 | -2 |
\(n\) | 1 (TM) | 3 (TM) | 0 (TM) | 4 (TM) |
Vậy \(n \in \left\{ {1;3;0;4} \right\}\).
Đề thi học kì 2 Toán 6 - Đề số 2 chương trình Kết nối tri thức là một công cụ quan trọng giúp học sinh lớp 6 ôn tập và củng cố kiến thức đã học trong suốt học kì. Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp học sinh làm quen với nhiều dạng đề và rèn luyện kỹ năng giải toán.
Đề thi thường bao gồm các phần sau:
Đề thi học kì 2 Toán 6 - Đề số 2 - Kết nối tri thức thường tập trung vào các chủ đề sau:
Để đạt kết quả tốt trong kỳ thi học kì, học sinh cần:
Dạng 1: Tính toán với số nguyên
Ví dụ: Tính (-5) + 3 - (-2) = ?
Lời giải: (-5) + 3 - (-2) = -5 + 3 + 2 = 0
Dạng 2: Giải bài toán về tỉ số và phần trăm
Ví dụ: Một cửa hàng bán được 200 sản phẩm, trong đó 40% là sản phẩm A. Hỏi cửa hàng đã bán được bao nhiêu sản phẩm A?
Lời giải: Số sản phẩm A đã bán được là: 200 x 40% = 80 sản phẩm
Việc ôn tập và luyện đề thường xuyên là rất quan trọng để học sinh nắm vững kiến thức và chuẩn bị tốt cho kỳ thi học kì. Khi luyện đề, học sinh sẽ làm quen với các dạng bài tập khác nhau, rèn luyện kỹ năng giải toán và phát hiện ra những lỗ hổng kiến thức cần bổ sung.
Giaitoan.edu.vn là một website cung cấp các tài liệu học tập trực tuyến chất lượng cao, bao gồm đề thi, bài giảng, bài tập và đáp án chi tiết. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em đạt kết quả cao trong học tập.
Hãy dành thời gian ôn tập và luyện đề một cách nghiêm túc. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 6!