Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 6 - Đề số 5, một công cụ hữu ích giúp các em học sinh ôn luyện và củng cố kiến thức đã học trong học kì. Đề thi được biên soạn theo chuẩn chương trình Toán 6, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao.
Với đề thi này, các em sẽ có cơ hội làm quen với cấu trúc đề thi thực tế, rèn luyện kỹ năng giải toán và tự đánh giá năng lực của bản thân. Đồng thời, đề thi còn đi kèm với đáp án chi tiết, giúp các em hiểu rõ phương pháp giải và khắc phục những sai lầm.
Phần I: Trắc nghiệm (4 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (4 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Trong các khẳng định sau, khẳng định nào đúng:
A. \(0 \in {\mathbb{N}^*}\)
B. \(0,5 \in \mathbb{N}\)
C. \(15 \in \mathbb{N}\)
D. \(\dfrac{3}{2} \in \mathbb{N}\)
Câu 2. Tập hợp các chữ số của số \(2022\) là:
A. \(\left\{ {2\,\,;\,\,0\,\,;\,\,2\,\,;\,\,2} \right\}\)
B. \(\left\{ {2\,\,;\,\,0} \right\}\)
C. \(\left\{ 2 \right\}\)
D.\(\left\{ 0 \right\}\)
Câu 3. Tìm ước chung lớn nhất của \(36\) và \(120\).
A. ƯCLN\(\left( {36\,,\,120} \right) = 6\)
B. ƯCLN\(\left( {36\,,120} \right) = 12\)
C. ƯCLN\(\left( {36\,,\,120} \right) = 18\)
D.ƯCLN\(\left( {36\,,120} \right) = 36\)
Câu 4. Kết quả phép tính \(\left( { - 46} \right) + 72 - 172 + \left( { - 54} \right)\) là:
A. \( - 200\)
B. \(0\)
C. \(100\)
D. \(200\)
Câu 5. Số nào chia hết cho cả \(2;3;5;9\) trong các số sau:
A. \(6400\)
B. \(3195\)
C. \(6480\)
D. \(9036\)
Câu 6. Sắp xếp các số sau theo thứ tự tăng dần: \( - 3\,;\, - 99;\,3\,;\, - 5;\,12;\, - 18\)
A. \( - 99\,;\, - 18\,;\, - 5\,;\, - \,3\,;\,12\)
B. \( - 99\,;\, - 18\,;\, - 5\,;\,\,3\,;\,12\)
C. \(12\,;\,3\,;\, - 3\,;\, - 5\,;\, - 18;\, - 99\)
D.\( - 99\,;\, - 18\,;\, - 5\,;\, - 3\,;\,3\,;\,12\)
Câu 7. Có tất cả bao nhiêu hình vuông được vẽ trong hình?
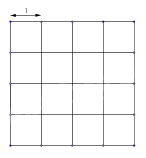
A. \(16\)
B. \(25\)
C. \(27\)
D. \(30\)
Câu 8. Hình bình hành có độ dài một cạnh \(10\,cm\) và chiều cao tương ứng là \(5\,cm\) thì diện tích của hình bình hành đó gấp mất lần diện tích của hình vuông có cạnh là \(5\,cm\).
A. \(2\)
B. \(3\)
C. \(4\)
D. \(5\)
Câu 9. Trong các hình dưới đây, hình nào có trục đối xứng?

A. A, B, E
B. H, E
C. A, H, E
D. B, H
Câu 10. Một khu vườn hình chữ nhật có chiều dài \(30m\) và chiều rộng \(25m\). Ở giữa khu vườn người ta xây một bồn hoa hình thoi có độ dài hai đường chéo là \(3m\) và \(4m\). Tính diện tích phần còn lại của khu vườn?

A. \(750\,{m^2}\)
B. \(744{m^2}\)
C. \(756{m^2}\)
D. \(700{m^2}\)
Phần II. Tự luận (6 điểm):
Bài 1. (1,0 điểm) Thực hiện phép tính:
a) \(2448:\left[ {119 - \left( {23 - 6} \right)} \right]\)
b) \({87.3^3} + 64.73 - {23.3^3}\)
Bài 2. (1,0 điểm) Tìm \(x\), biết:
a) \(272 - \left( {4x + 15} \right) = 45\)
b) \({5^x} + {5^{x + 2}} = 650\)
Bài 3. (1,5 điểm) Tìm số tự nhiên \(x\), biết:
a) \(x\) nhỏ nhất khác \(0\) và \(x\,\, \vdots \,\,126,\,\,x\,\, \vdots \,\,198\)
b) \(90\,\, \vdots \,\,x,\,\,150\,\, \vdots \,\,x\) và \(5 < x < 30\)
Bài 4. (2 điểm) Bác An muốn lát sân phía trước nhà. Sân nhà có hình vẽ như sau:

Biết hình vuông lớn có chu vi là \(16\,m\), hai hình vuông nhỏ bằng nhau có chu vi là \(8\,m\). Bác muốn lát sân bằng các viên gạch có hình vuông có cạnh dài \(20\,cm\), giá tiền mỗi viên gạch là \(6000\) đồng. Tính số tiền bác An cần để mua đủ gạch lát toàn bộ sân nhà? (Mạch vữa giữa các viên gạch không đáng kể.)
Bài 5. (0,5 điểm) Chứng minh rằng với mọi số tự nhiên \(n\) thì \(7n + 10\) và \(5n + 7\) là các số nguyên tố cùng nhau.
Phần I: Trắc nghiệm
1. C | 2. B | 3. A | 4. A | 5. C | 6. D | 7. D | 8. A | 9. C | 10. B |
Câu 1
Phương pháp:
Sử dụng định nghĩa và kí hiệu phần tử thuộc hay không thuộc một tập hợp.
Cách giải:
Vì \(\mathbb{N} = \left\{ {0;1;2;3;4;...} \right\}\) nên \(15 \in \mathbb{N}\).
Chọn C.
Câu 2
Phương pháp:
Biểu diễn tập hợpbằng cách liệt kê: Liệt kê các phần tử của tập hợp trong dấu { }; mỗi phần tử được liệt kê 1 lần, theo thứ tự tùy ý; các phần tử ngăn cách nhau bởi dấu ;
Cách giải:
Tập hợp các chữ số của số \(2022\) là: \(\left\{ {2\,\,;\,\,0} \right\}\)
Chọn B.
Câu 3
Phương pháp:
Vận dụng quy tắc tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Cách giải:
Tích đó là ƯCLN phải tìm.
Ta có: \(36 = 3.12 = 3.3.4 = {2^2}{.3^2}\)
\(120 = 12.10 = 2.6.2.5 = {2^3}.3.5\)
Vậy ƯCLN\(\left( {36\,,\,120} \right) = 2.3 = 6\)
Chọn A.
Câu 4
Phương pháp:
Khi thực hiện phép tính ta cần lưu ý:
+ Đổi vị trí các số hạng (nếu cần).
+ Đặt dấu ngoặc một cách thích hợp.
Cách giải:
Ta có: \(\left( { - 46} \right) + 72 - 172 + \left( { - 54} \right)\)
\( = \left( { - 46 - 54} \right) + \left( {72 - 172} \right)\)
\(\begin{array}{l} = - 100 - 100\\ = - 200\end{array}\)
Chọn A.
Câu 5
Phương pháp:
Sử dụng dấu hiệu chia hết cho \(2;3;5;9\).
Cách giải:
Ta có số \(6480\) có chữ số tận cùng là \(0\) nên \(6480\) chia hết cho cả \(2\) và \(5\).
Lại có \(6 + 4 + 8 + 0 = 18\) chia hết cho cả \(3\) và \(9\).
Vậy \(6480\) chia hết cho cả bốn số \(2;3;5;9\).
Chọn C.
Câu 6
Phương pháp:
So sánh các số nguyên âm với nhau \( \to \) thứ tự tăng dần của các số nguyên âm
So sánh các số nguyên dương với nhau \( \to \) thứ tự tăng dần của các số nguyên dương.
Các số nguyên dương luôn lớn hơn các số nguyên âm.
Cách giải:
+ So sánh các số nguyên âm: \( - 3\,;\, - 99\,;\, - 5\,;\, - 18\)
Ta có: \(3 < 5 < 18 < 99\) nên \( - 3 > - 5 > - 18 > - 99\) (1)
+ So sánh các số nguyên dương: \(3\,;\,12\)
Ta có: \(3 < 12\) (2)
Từ (1) và (2), ta có: \( - 99 < - 18 < - 5 < - 3 < 3 < 12\)
Vậy các số sắp xếp theo thứ tự tăng dần là: \( - 99\,;\, - 18\,;\, - 5\,;\, - 3\,;\,3\,;\,12\).
Chọn D.
Câu 7
Phương pháp:
Nhận biết được hình vuông.
Cách giải:
Có 16 hình vuông cạnh 1.
Có 9 hình vuông cạnh 2.
Có 4 hình vuông cạnh 3.
Có 1 hình vuông cạnh 4.
\( \Rightarrow \) Có \(16 + 9 + 4 + 1 = 30\) hình vuông.
Chọn D.
Câu 8
Phương pháp:
Sử dụng công thức tính diện tích hình hành hành có hai cạnh là \(a,b\) và chiều cao tương ứng với cạnh \(a\) là \(h\) thì \(S = a.h\)
Sử dụng công thức tính diện tích hình vuông có cạnh là \(a\) thì \(S = a.a\)
Cách giải:
Diện tích của hình bình hành là: \(10.5 = 50\left( {{m^2}} \right)\)
Diện tích của hình vuông là: \(5.5 = 25\left( {{m^2}} \right)\)
Ta có: \(50:25 = 2\) (lần)
Vậy diện tích của hình bình hành gấp \(2\) lần diện tích của hình vuông.
Chọn A.
Câu 9
Phương pháp:
Sử dụng định nghĩa đối xứng trục
Cách giải:
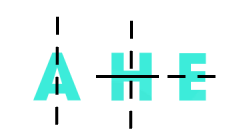
Nhận thấy hình A, H, E có trục đối xứng.
Chọn C.
Câu 10
Phương pháp:
Sử dụng công thức tính diện tích hình chữ nhật, công thức tính diện tích hình thoi.
Cách giải:
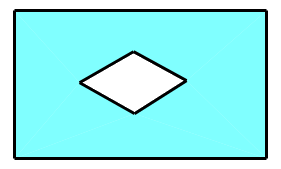
Diện tích khu vườn hình chữ nhật là: \(30.25 = 750\,\left( {{m^{`2}}} \right)\).
Diện tích bồn hoa hình thoi là: \(\dfrac{1}{2}.3.4 = 6\,\left( {{m^2}} \right)\).
Diện tích phần còn lại của khu vườn là: \(750\, - 6 = 744\left( {{m^{`2}}} \right)\).
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp:
Biểu thức có ngoặc thực hiện theo thứ tự \(\left( {\,\,\,} \right) \to \left[ {\,\,\,} \right] \to \left\{ {\,\,\,} \right\}\)
Vận dụng quy tắc bỏ ngoặc có dấu “\( - \)” ở trước.
Thực hiện các phép toán với số nguyên.
Vận dụng kiến thức lũy thừa của một số tự nhiên.
Cách giải:
a) \(2448:\left[ {119 - \left( {23 - 6} \right)} \right]\)
\(\begin{array}{l} = 2448:\left( {119 - 17} \right)\\ = 2448:102\\ = 24\end{array}\)
b) \({87.3^3} + 64.73 - {23.3^3}\)
\(\begin{array}{l} = \left( {{{87.3}^3} - {{23.3}^3}} \right) + 64.73\\ = \left( {87.27 - 23.27} \right) + 64.73\\ = 27.\left( {87 - 23} \right) + 64.73\\ = 27.64 + 64.73\\ = 64.\left( {27 + 73} \right)\\ = 64.100\\ = 6400\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số tự nhiên.
b) Vận dụng kiến thức lũy thừa với số mũ tự nhiên
Hai lũy thừa cùng cơ số bằng nhau khi số mũ của chúng bằng nhau.
Cách giải:
a) \(272 - \left( {4x + 15} \right) = 45\)
\(\begin{array}{l}4x + 15 = 272 - 45\\4x + 15 = 227\\4x = 227 - 15\\4x = 212\\x = 212:4\\x = 53\end{array}\)
Vậy \(x = 53\)
b) \({5^x} + {5^{x + 2}} = 650\)
\(\begin{array}{l}{5^x} + {5^x}{.5^2} = 650\\{5^x}.\left( {1 + 25} \right) = 650\\{5^x}.26 = 650\\{5^x} = 650:26\\{5^x} = 25\\{5^x} = {5^2}\\x = 2\end{array}\)
Vậy \(x = 2\)
Bài 3
Phương pháp:
a) Vận dụng quy tắc tìm bội chung nhỏ nhất của hai số.
b) Vận dụng quy tắc tìm ước chung lớn nhất của hai số.
Cách giải:
a) Vì \(x\) nhỏ nhất khác \(0\) và \(x\,\, \vdots \,\,126,\,\,x\,\, \vdots \,\,198\) \( \Rightarrow x = \)BCNN\(\left( {126,198} \right)\)
Ta có: \(\left\{ \begin{array}{l}126 = {2.3^2}.7\\198 = {2.3^2}.11\end{array} \right. \Rightarrow \)BCNN\(\left( {126,198} \right) = {2.3^2}.7.11 = 1386\)
Vậy \(x = 1286\).
b) Vì \(90\,\, \vdots \,\,x,\,\,150\,\, \vdots \,\,x\) \( \Rightarrow x \in \)ƯC\(\left( {90;150} \right)\)
Ta có: \(\left\{ \begin{array}{l}90 = {2.3^2}.5\\150 = {2.3.5^2}\end{array} \right. \Rightarrow \)ƯCLN\(\left( {90,150} \right) = 2.3.5 = 30\)
\( \Rightarrow \)ƯC\(\left( {90,150} \right) = \)Ư\(\left( {30} \right) = \left\{ {1;2;3;5;6;10;15;30} \right\}\)
Mà \(5 < x < 30 \Rightarrow x \in \left\{ {6;10;15} \right\}\)
Vậy \(x \in \left\{ {6;10;15} \right\}\)
Bài 4
Phương pháp:
Sử dụng công thức tính chu vi của hình vuông, diện tích của hình vuông.
Cách giải:
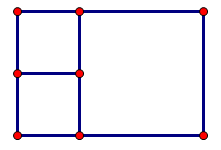
Cạnh của hình vuông lớn có độ dài là: \(16:4 = 4\,\left( m \right)\)
Diện tích của hình vuông lớn là: \(4.4 = 16\left( {{m^2}} \right)\)
Cạnh của hình vuông nhỏ có độ dài là: \(8:4 = 2\left( m \right)\)
Diện tích của hình vuông nhỏ là: \(2.2 = 4\left( {{m^2}} \right)\)
Vì hai hình vuông bằng nhau nên tổng diện tích của hai hình vuông nhỏ là: \(4 + 4 = 8\left( {{m^2}} \right)\)
Diện tích của sân là: \(16 + 8 = 24\left( {{m^2}} \right)\)
Diện tích của 1 viên gạch là: \(20.20 = 400\,\left( {c{m^2}} \right) = 0,04\left( {{m^2}} \right)\)
Số viên gạch để lát toàn bộ sân là: \(24:0,04 = 600\) (viên gạch)
Số tiền bác An cần để mua đủ gạch lát toàn bộ sân là: \(600.6000 = 3\,600\,000\) (đồng)
Bài 5
Phương pháp:
Hai số là số nguyên tố cùng nhau nếu chúng có ước chung lớn nhất là \(1\)
Cách giải:
Gọi ƯCLN\(\left( {7n + 10;5n + 7} \right) = d \Rightarrow \left\{ \begin{array}{l}\left( {7n + 10} \right)\,\, \vdots \,\,d\\\left( {5n + 7} \right)\,\, \vdots \,\,d\end{array} \right.\)
\( \Rightarrow 5\left( {7n + 10} \right) - 7\left( {5n + 7} \right)\,\, \vdots \,\,d\)
\(35n + 50 - 35n - 49\,\, \vdots \,\,d\)
\( \Rightarrow 1\,\, \vdots \,\,d \Rightarrow d = 1\)
Vậy \(7n + 10\) và \(5n + 7\) là hai số nguyên tố cùng nhau.
Phần I: Trắc nghiệm (4 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Trong các khẳng định sau, khẳng định nào đúng:
A. \(0 \in {\mathbb{N}^*}\)
B. \(0,5 \in \mathbb{N}\)
C. \(15 \in \mathbb{N}\)
D. \(\dfrac{3}{2} \in \mathbb{N}\)
Câu 2. Tập hợp các chữ số của số \(2022\) là:
A. \(\left\{ {2\,\,;\,\,0\,\,;\,\,2\,\,;\,\,2} \right\}\)
B. \(\left\{ {2\,\,;\,\,0} \right\}\)
C. \(\left\{ 2 \right\}\)
D.\(\left\{ 0 \right\}\)
Câu 3. Tìm ước chung lớn nhất của \(36\) và \(120\).
A. ƯCLN\(\left( {36\,,\,120} \right) = 6\)
B. ƯCLN\(\left( {36\,,120} \right) = 12\)
C. ƯCLN\(\left( {36\,,\,120} \right) = 18\)
D.ƯCLN\(\left( {36\,,120} \right) = 36\)
Câu 4. Kết quả phép tính \(\left( { - 46} \right) + 72 - 172 + \left( { - 54} \right)\) là:
A. \( - 200\)
B. \(0\)
C. \(100\)
D. \(200\)
Câu 5. Số nào chia hết cho cả \(2;3;5;9\) trong các số sau:
A. \(6400\)
B. \(3195\)
C. \(6480\)
D. \(9036\)
Câu 6. Sắp xếp các số sau theo thứ tự tăng dần: \( - 3\,;\, - 99;\,3\,;\, - 5;\,12;\, - 18\)
A. \( - 99\,;\, - 18\,;\, - 5\,;\, - \,3\,;\,12\)
B. \( - 99\,;\, - 18\,;\, - 5\,;\,\,3\,;\,12\)
C. \(12\,;\,3\,;\, - 3\,;\, - 5\,;\, - 18;\, - 99\)
D.\( - 99\,;\, - 18\,;\, - 5\,;\, - 3\,;\,3\,;\,12\)
Câu 7. Có tất cả bao nhiêu hình vuông được vẽ trong hình?
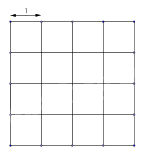
A. \(16\)
B. \(25\)
C. \(27\)
D. \(30\)
Câu 8. Hình bình hành có độ dài một cạnh \(10\,cm\) và chiều cao tương ứng là \(5\,cm\) thì diện tích của hình bình hành đó gấp mất lần diện tích của hình vuông có cạnh là \(5\,cm\).
A. \(2\)
B. \(3\)
C. \(4\)
D. \(5\)
Câu 9. Trong các hình dưới đây, hình nào có trục đối xứng?

A. A, B, E
B. H, E
C. A, H, E
D. B, H
Câu 10. Một khu vườn hình chữ nhật có chiều dài \(30m\) và chiều rộng \(25m\). Ở giữa khu vườn người ta xây một bồn hoa hình thoi có độ dài hai đường chéo là \(3m\) và \(4m\). Tính diện tích phần còn lại của khu vườn?

A. \(750\,{m^2}\)
B. \(744{m^2}\)
C. \(756{m^2}\)
D. \(700{m^2}\)
Phần II. Tự luận (6 điểm):
Bài 1. (1,0 điểm) Thực hiện phép tính:
a) \(2448:\left[ {119 - \left( {23 - 6} \right)} \right]\)
b) \({87.3^3} + 64.73 - {23.3^3}\)
Bài 2. (1,0 điểm) Tìm \(x\), biết:
a) \(272 - \left( {4x + 15} \right) = 45\)
b) \({5^x} + {5^{x + 2}} = 650\)
Bài 3. (1,5 điểm) Tìm số tự nhiên \(x\), biết:
a) \(x\) nhỏ nhất khác \(0\) và \(x\,\, \vdots \,\,126,\,\,x\,\, \vdots \,\,198\)
b) \(90\,\, \vdots \,\,x,\,\,150\,\, \vdots \,\,x\) và \(5 < x < 30\)
Bài 4. (2 điểm) Bác An muốn lát sân phía trước nhà. Sân nhà có hình vẽ như sau:

Biết hình vuông lớn có chu vi là \(16\,m\), hai hình vuông nhỏ bằng nhau có chu vi là \(8\,m\). Bác muốn lát sân bằng các viên gạch có hình vuông có cạnh dài \(20\,cm\), giá tiền mỗi viên gạch là \(6000\) đồng. Tính số tiền bác An cần để mua đủ gạch lát toàn bộ sân nhà? (Mạch vữa giữa các viên gạch không đáng kể.)
Bài 5. (0,5 điểm) Chứng minh rằng với mọi số tự nhiên \(n\) thì \(7n + 10\) và \(5n + 7\) là các số nguyên tố cùng nhau.
Phần I: Trắc nghiệm
1. C | 2. B | 3. A | 4. A | 5. C | 6. D | 7. D | 8. A | 9. C | 10. B |
Câu 1
Phương pháp:
Sử dụng định nghĩa và kí hiệu phần tử thuộc hay không thuộc một tập hợp.
Cách giải:
Vì \(\mathbb{N} = \left\{ {0;1;2;3;4;...} \right\}\) nên \(15 \in \mathbb{N}\).
Chọn C.
Câu 2
Phương pháp:
Biểu diễn tập hợpbằng cách liệt kê: Liệt kê các phần tử của tập hợp trong dấu { }; mỗi phần tử được liệt kê 1 lần, theo thứ tự tùy ý; các phần tử ngăn cách nhau bởi dấu ;
Cách giải:
Tập hợp các chữ số của số \(2022\) là: \(\left\{ {2\,\,;\,\,0} \right\}\)
Chọn B.
Câu 3
Phương pháp:
Vận dụng quy tắc tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Cách giải:
Tích đó là ƯCLN phải tìm.
Ta có: \(36 = 3.12 = 3.3.4 = {2^2}{.3^2}\)
\(120 = 12.10 = 2.6.2.5 = {2^3}.3.5\)
Vậy ƯCLN\(\left( {36\,,\,120} \right) = 2.3 = 6\)
Chọn A.
Câu 4
Phương pháp:
Khi thực hiện phép tính ta cần lưu ý:
+ Đổi vị trí các số hạng (nếu cần).
+ Đặt dấu ngoặc một cách thích hợp.
Cách giải:
Ta có: \(\left( { - 46} \right) + 72 - 172 + \left( { - 54} \right)\)
\( = \left( { - 46 - 54} \right) + \left( {72 - 172} \right)\)
\(\begin{array}{l} = - 100 - 100\\ = - 200\end{array}\)
Chọn A.
Câu 5
Phương pháp:
Sử dụng dấu hiệu chia hết cho \(2;3;5;9\).
Cách giải:
Ta có số \(6480\) có chữ số tận cùng là \(0\) nên \(6480\) chia hết cho cả \(2\) và \(5\).
Lại có \(6 + 4 + 8 + 0 = 18\) chia hết cho cả \(3\) và \(9\).
Vậy \(6480\) chia hết cho cả bốn số \(2;3;5;9\).
Chọn C.
Câu 6
Phương pháp:
So sánh các số nguyên âm với nhau \( \to \) thứ tự tăng dần của các số nguyên âm
So sánh các số nguyên dương với nhau \( \to \) thứ tự tăng dần của các số nguyên dương.
Các số nguyên dương luôn lớn hơn các số nguyên âm.
Cách giải:
+ So sánh các số nguyên âm: \( - 3\,;\, - 99\,;\, - 5\,;\, - 18\)
Ta có: \(3 < 5 < 18 < 99\) nên \( - 3 > - 5 > - 18 > - 99\) (1)
+ So sánh các số nguyên dương: \(3\,;\,12\)
Ta có: \(3 < 12\) (2)
Từ (1) và (2), ta có: \( - 99 < - 18 < - 5 < - 3 < 3 < 12\)
Vậy các số sắp xếp theo thứ tự tăng dần là: \( - 99\,;\, - 18\,;\, - 5\,;\, - 3\,;\,3\,;\,12\).
Chọn D.
Câu 7
Phương pháp:
Nhận biết được hình vuông.
Cách giải:
Có 16 hình vuông cạnh 1.
Có 9 hình vuông cạnh 2.
Có 4 hình vuông cạnh 3.
Có 1 hình vuông cạnh 4.
\( \Rightarrow \) Có \(16 + 9 + 4 + 1 = 30\) hình vuông.
Chọn D.
Câu 8
Phương pháp:
Sử dụng công thức tính diện tích hình hành hành có hai cạnh là \(a,b\) và chiều cao tương ứng với cạnh \(a\) là \(h\) thì \(S = a.h\)
Sử dụng công thức tính diện tích hình vuông có cạnh là \(a\) thì \(S = a.a\)
Cách giải:
Diện tích của hình bình hành là: \(10.5 = 50\left( {{m^2}} \right)\)
Diện tích của hình vuông là: \(5.5 = 25\left( {{m^2}} \right)\)
Ta có: \(50:25 = 2\) (lần)
Vậy diện tích của hình bình hành gấp \(2\) lần diện tích của hình vuông.
Chọn A.
Câu 9
Phương pháp:
Sử dụng định nghĩa đối xứng trục
Cách giải:

Nhận thấy hình A, H, E có trục đối xứng.
Chọn C.
Câu 10
Phương pháp:
Sử dụng công thức tính diện tích hình chữ nhật, công thức tính diện tích hình thoi.
Cách giải:

Diện tích khu vườn hình chữ nhật là: \(30.25 = 750\,\left( {{m^{`2}}} \right)\).
Diện tích bồn hoa hình thoi là: \(\dfrac{1}{2}.3.4 = 6\,\left( {{m^2}} \right)\).
Diện tích phần còn lại của khu vườn là: \(750\, - 6 = 744\left( {{m^{`2}}} \right)\).
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp:
Biểu thức có ngoặc thực hiện theo thứ tự \(\left( {\,\,\,} \right) \to \left[ {\,\,\,} \right] \to \left\{ {\,\,\,} \right\}\)
Vận dụng quy tắc bỏ ngoặc có dấu “\( - \)” ở trước.
Thực hiện các phép toán với số nguyên.
Vận dụng kiến thức lũy thừa của một số tự nhiên.
Cách giải:
a) \(2448:\left[ {119 - \left( {23 - 6} \right)} \right]\)
\(\begin{array}{l} = 2448:\left( {119 - 17} \right)\\ = 2448:102\\ = 24\end{array}\)
b) \({87.3^3} + 64.73 - {23.3^3}\)
\(\begin{array}{l} = \left( {{{87.3}^3} - {{23.3}^3}} \right) + 64.73\\ = \left( {87.27 - 23.27} \right) + 64.73\\ = 27.\left( {87 - 23} \right) + 64.73\\ = 27.64 + 64.73\\ = 64.\left( {27 + 73} \right)\\ = 64.100\\ = 6400\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số tự nhiên.
b) Vận dụng kiến thức lũy thừa với số mũ tự nhiên
Hai lũy thừa cùng cơ số bằng nhau khi số mũ của chúng bằng nhau.
Cách giải:
a) \(272 - \left( {4x + 15} \right) = 45\)
\(\begin{array}{l}4x + 15 = 272 - 45\\4x + 15 = 227\\4x = 227 - 15\\4x = 212\\x = 212:4\\x = 53\end{array}\)
Vậy \(x = 53\)
b) \({5^x} + {5^{x + 2}} = 650\)
\(\begin{array}{l}{5^x} + {5^x}{.5^2} = 650\\{5^x}.\left( {1 + 25} \right) = 650\\{5^x}.26 = 650\\{5^x} = 650:26\\{5^x} = 25\\{5^x} = {5^2}\\x = 2\end{array}\)
Vậy \(x = 2\)
Bài 3
Phương pháp:
a) Vận dụng quy tắc tìm bội chung nhỏ nhất của hai số.
b) Vận dụng quy tắc tìm ước chung lớn nhất của hai số.
Cách giải:
a) Vì \(x\) nhỏ nhất khác \(0\) và \(x\,\, \vdots \,\,126,\,\,x\,\, \vdots \,\,198\) \( \Rightarrow x = \)BCNN\(\left( {126,198} \right)\)
Ta có: \(\left\{ \begin{array}{l}126 = {2.3^2}.7\\198 = {2.3^2}.11\end{array} \right. \Rightarrow \)BCNN\(\left( {126,198} \right) = {2.3^2}.7.11 = 1386\)
Vậy \(x = 1286\).
b) Vì \(90\,\, \vdots \,\,x,\,\,150\,\, \vdots \,\,x\) \( \Rightarrow x \in \)ƯC\(\left( {90;150} \right)\)
Ta có: \(\left\{ \begin{array}{l}90 = {2.3^2}.5\\150 = {2.3.5^2}\end{array} \right. \Rightarrow \)ƯCLN\(\left( {90,150} \right) = 2.3.5 = 30\)
\( \Rightarrow \)ƯC\(\left( {90,150} \right) = \)Ư\(\left( {30} \right) = \left\{ {1;2;3;5;6;10;15;30} \right\}\)
Mà \(5 < x < 30 \Rightarrow x \in \left\{ {6;10;15} \right\}\)
Vậy \(x \in \left\{ {6;10;15} \right\}\)
Bài 4
Phương pháp:
Sử dụng công thức tính chu vi của hình vuông, diện tích của hình vuông.
Cách giải:

Cạnh của hình vuông lớn có độ dài là: \(16:4 = 4\,\left( m \right)\)
Diện tích của hình vuông lớn là: \(4.4 = 16\left( {{m^2}} \right)\)
Cạnh của hình vuông nhỏ có độ dài là: \(8:4 = 2\left( m \right)\)
Diện tích của hình vuông nhỏ là: \(2.2 = 4\left( {{m^2}} \right)\)
Vì hai hình vuông bằng nhau nên tổng diện tích của hai hình vuông nhỏ là: \(4 + 4 = 8\left( {{m^2}} \right)\)
Diện tích của sân là: \(16 + 8 = 24\left( {{m^2}} \right)\)
Diện tích của 1 viên gạch là: \(20.20 = 400\,\left( {c{m^2}} \right) = 0,04\left( {{m^2}} \right)\)
Số viên gạch để lát toàn bộ sân là: \(24:0,04 = 600\) (viên gạch)
Số tiền bác An cần để mua đủ gạch lát toàn bộ sân là: \(600.6000 = 3\,600\,000\) (đồng)
Bài 5
Phương pháp:
Hai số là số nguyên tố cùng nhau nếu chúng có ước chung lớn nhất là \(1\)
Cách giải:
Gọi ƯCLN\(\left( {7n + 10;5n + 7} \right) = d \Rightarrow \left\{ \begin{array}{l}\left( {7n + 10} \right)\,\, \vdots \,\,d\\\left( {5n + 7} \right)\,\, \vdots \,\,d\end{array} \right.\)
\( \Rightarrow 5\left( {7n + 10} \right) - 7\left( {5n + 7} \right)\,\, \vdots \,\,d\)
\(35n + 50 - 35n - 49\,\, \vdots \,\,d\)
\( \Rightarrow 1\,\, \vdots \,\,d \Rightarrow d = 1\)
Vậy \(7n + 10\) và \(5n + 7\) là hai số nguyên tố cùng nhau.
Đề thi học kì 1 Toán 6 - Đề số 5 là một bài kiểm tra đánh giá kiến thức và kỹ năng của học sinh sau nửa học kì đầu tiên của chương trình Toán 6. Đề thi thường bao gồm các chủ đề chính như:
Cấu trúc đề thi thường bao gồm các dạng bài tập khác nhau như trắc nghiệm, tự luận, bài toán thực tế. Tỷ lệ phân bổ điểm cho từng chủ đề có thể khác nhau tùy theo chương trình học của từng trường.
Để giúp học sinh ôn tập và làm bài thi hiệu quả, Giaitoan.edu.vn cung cấp hướng dẫn giải chi tiết cho từng câu hỏi trong Đề thi học kì 1 Toán 6 - Đề số 5. Hướng dẫn giải bao gồm:
Ngoài ra, chúng tôi cũng cung cấp các bài giảng lý thuyết, các bài tập luyện tập và các mẹo giải toán để giúp học sinh nắm vững kiến thức và kỹ năng cần thiết.
Luyện tập với Đề thi học kì 1 Toán 6 - Đề số 5 mang lại nhiều lợi ích cho học sinh:
Để đạt kết quả tốt nhất trong kỳ thi học kì 1 Toán 6, học sinh cần lưu ý một số mẹo sau:
Ngoài Đề thi học kì 1 Toán 6 - Đề số 5, Giaitoan.edu.vn còn cung cấp nhiều tài liệu ôn tập Toán 6 hữu ích khác như:
Đề thi học kì 1 Toán 6 - Đề số 5 là một công cụ hữu ích giúp học sinh ôn tập và chuẩn bị tốt nhất cho kỳ thi. Hãy luyện tập thường xuyên và áp dụng các mẹo làm bài thi hiệu quả để đạt kết quả tốt nhất!