Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 6 - Đề số 17, một công cụ hữu ích giúp các em học sinh ôn luyện và củng cố kiến thức đã học trong học kì. Đề thi được biên soạn theo chuẩn chương trình Toán 6, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao.
Với đáp án chi tiết đi kèm, các em có thể tự đánh giá năng lực của mình và tìm ra những điểm cần cải thiện. Đây là cơ hội tuyệt vời để các em tự tin bước vào kỳ thi học kì với kết quả tốt nhất.
Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x < 2} \right\}\). Tập hợp A viết dưới dạng liệt kê các phần tử là:
\(A = \left\{ { - 2; - 1;0;1} \right\}\).
\(A = \left\{ { - 1;0;1} \right\}\).
\(A = \left\{ { - 2; - 1;0} \right\}\).
\(A = \left\{ { - 2; - 1;1} \right\}\).
Bội chung nhỏ nhất của 12 và 36 là:
12.
6.
36.
72.
Số đối của số 53 là:
-53.
-35.
31.
13.
Cho biết nhiệt độ của 4 hành tinh như sau:

Hành tinh có nhiệt độ thấp nhất là:
Sao Hỏa.
Sao Kim.
Sao Thiên Vương.
Sao Thủy.
Các số 2; 9; 0; -15; -4 được sắp xếp theo thứ tự giảm dần là
0; 2; 9; -4; -15.
9; 2; 0; -4; -15.
-15; -4; 0; 2; 9.
2; 9; 0; -4; -15.
Trong các hình dưới đây, hình có tâm đối xứng là:

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Trong các hình dưới đây, hình nào là hình thoi?

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Trong các hình sau, hình nào có các góc đều bằng \(60^\circ \)?
Hình chữ nhật.
Hình vuông.
Tam giác đều.
Lục giác đều.
Thực hiện phép tính (tính hợp lí nếu có thể):
a) \( - 132 + 125\)
b) \({2^3}.\left( { - 135} \right) + {35.2^3}\)
c) \(\left[ {\left( { - 235} \right) + 171} \right] - \left( {71 - 235} \right)\)
d) \(160:\left\{ {17 + \left[ {{3^2}.5 - \left( {14 + {2^{11}}:{2^8}} \right)} \right]} \right\}\)
Tìm số nguyên \(x\), biết:
a) \(x - 10 = - 65\)
b) \(32:\left( {x + 125} \right) = - {4^2}\)
c) \(20 - 5\left( {2 - x} \right) = 45\)
Một trường tổ chức cho học sinh đi học tập trải nghiệm. Ban tổ chức thấy rằng nếu xếp mỗi xe ô tô 36 học sinh; 40 học sinh hoặc 48 học sinh thì đều đủ chỗ, không thừa ai. Biết số học sinh của trường vào khoảng từ 1200 đến 1500 em. Hỏi trường đó có bao nhiêu học sinh?
Bác Khánh có mảnh vườn có hình dạng ghép bởi một hình chữ nhật và một hình thang. Kích thước của mảnh vườn được mô tả bằng bản vẽ hình sau.
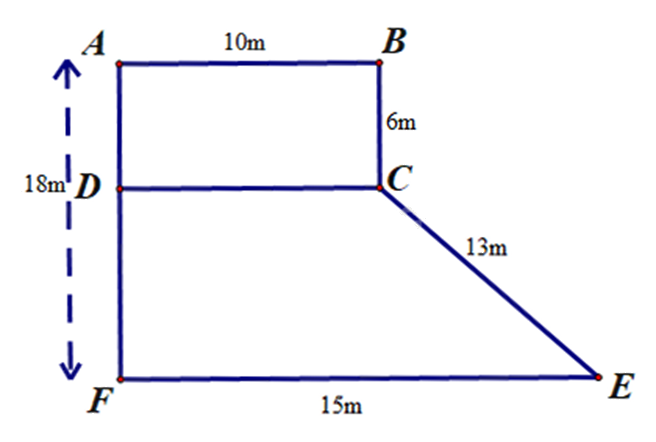
a) Tính diện tích phần vườn hình chữ nhật ABCD.
b) Bác Khánh muốn mua lưới mắt cáo để rào xung quanh mảnh vườn, tính chiều dài hàng rào?
c) Qua tìm hiểu Bác Khánh thấy người ta trồng ngô thì thu được 25 nghìn đồng/m\(^2\), trồng mía thì thu được 30 nghìn đồng/m\(^2\), trồng thanh long thì thu được 40 nghìn đồng/m\(^2\). Em hãy giúp Bác Khánh chọn phương án có doanh thu tốt hơn trong hai phương án sau:
+ Phương án 1: Trồng mía trên cả mảnh vườn
+ Phương án 2: Trồng ngô trên phần mảnh vườn hình thang và trồng thanh long trên mảnh vườn hình chữ nhật.
Chứng tỏ rằng với mọi \(n \in \mathbb{N}\) thì \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.
Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x < 2} \right\}\). Tập hợp A viết dưới dạng liệt kê các phần tử là:
\(A = \left\{ { - 2; - 1;0;1} \right\}\).
\(A = \left\{ { - 1;0;1} \right\}\).
\(A = \left\{ { - 2; - 1;0} \right\}\).
\(A = \left\{ { - 2; - 1;1} \right\}\).
Đáp án : A
Liệt kê các số nguyên thỏa mãn \( - 2 \le x < 2\).
Tập hợp \(A = \left\{ { - 2; - 1;0;1} \right\}\).
Đáp án A
Bội chung nhỏ nhất của 12 và 36 là:
12.
6.
36.
72.
Đáp án : C
Kiểm tra 36 chia hết cho 12.
Vì 36 chia hết cho 12 nên bội chung nhỏ nhất của 12 và 36 là 36.
Đáp án C
Số đối của số 53 là:
-53.
-35.
31.
13.
Đáp án : A
Số đối của a là –a.
Số đối của 53 là -53.
Đáp án A
Cho biết nhiệt độ của 4 hành tinh như sau:

Hành tinh có nhiệt độ thấp nhất là:
Sao Hỏa.
Sao Kim.
Sao Thiên Vương.
Sao Thủy.
Đáp án : C
So sánh các số nguyên âm:
Nếu a và b là các số nguyên dương và a > b thì –a < -b.
Vì 87 < 184 < 220 < 224 nên -87 > -184 > -220 > -224.
Vậy hành tinh có nhiệt độ thấp nhất là Sao Thiên Vương (\( - 224^\circ C\)).
Đáp án C
Các số 2; 9; 0; -15; -4 được sắp xếp theo thứ tự giảm dần là
0; 2; 9; -4; -15.
9; 2; 0; -4; -15.
-15; -4; 0; 2; 9.
2; 9; 0; -4; -15.
Đáp án : B
Chia làm 2 nhóm: các số nguyên dương và nguyên âm để so sánh.
Ta chia các số thành hai nhóm:
+ Nhóm 1: 2; 9. Ta có: 2 < 9.
+ Nhóm 2: -15; -4. Ta có: 4 < 15 nên -4 > -15.
Vậy các số sắp xếp theo thứ tự giảm dần là 9; 2; 0; -4; -15.
Đáp án B
Trong các hình dưới đây, hình có tâm đối xứng là:

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đáp án : A
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
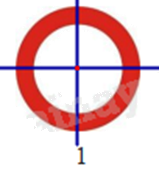
Hình có tâm đối xứng là hình 1.
Đáp án A
Trong các hình dưới đây, hình nào là hình thoi?

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đáp án : C
Hình thoi là hình có 4 cạnh bằng nhau.
Hình 3 là hình thoi.
Đáp án C
Trong các hình sau, hình nào có các góc đều bằng \(60^\circ \)?
Hình chữ nhật.
Hình vuông.
Tam giác đều.
Lục giác đều.
Đáp án : C
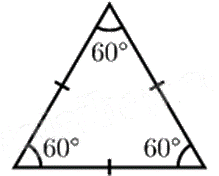
Hình có các góc đều bằng \(60^\circ \) là tam giác đều.
Đáp án C
Thực hiện phép tính (tính hợp lí nếu có thể):
a) \( - 132 + 125\)
b) \({2^3}.\left( { - 135} \right) + {35.2^3}\)
c) \(\left[ {\left( { - 235} \right) + 171} \right] - \left( {71 - 235} \right)\)
d) \(160:\left\{ {17 + \left[ {{3^2}.5 - \left( {14 + {2^{11}}:{2^8}} \right)} \right]} \right\}\)
a) Sử dụng quy tắc cộng hai số nguyên khác dấu.
Để cộng hai số nguyên khác dấu, ta làm như sau:
Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại.
Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn.
Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm.
b) Tính lũy thừa, áp dụng tính chất phân phối của phép nhân với phép cộng để tính.
c) Phá ngoặc sau đó sử dụng tính chất của kết hợp của phép cộng để nhóm.
d) Sử dụng các quy tắc tính với số nguyên và thứ tự thực hiện phép tính:
Nếu biểu thức có các dấu ngoặc: ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự:
( ) → [ ] → { }
a) \( - 132 + 125\)\( = - \left( {132 - 125} \right) = - 7\)
b) \({2^3}.\left( { - 135} \right) + {35.2^3}\)
\(\begin{array}{l} = 8.\left( { - 135} \right) + 35.8\\ = 8\left( { - 135 + 35} \right)\\ = 8.\left( { - 100} \right)\\ = - 800\end{array}\)
c) \(\left[ {\left( { - 235} \right) + 171} \right] - \left( {71 - 235} \right)\)
\(\begin{array}{l} = - 235 + 171 - 71 - 235\\ = \left( { - 235 + 235} \right) + \left( {171 - 71} \right)\\ = 0 + 100\\ = 100\end{array}\)
d) \(160:\left\{ {17 + \left[ {{3^2}.5 - \left( {14 + {2^{11}}:{2^8}} \right)} \right]} \right\}\)
\(\begin{array}{l} = 160:\{ 17 + [{3^2}.5 - (14 + {2^3})]\} \\ = 160:\left\{ {17 + \left[ {9.5 - \left( {14 + 8} \right)} \right]} \right\}\\ = 160:\left\{ {17 + \left[ {45 - 22} \right]} \right\}\\ = 160:\left\{ {17 + 23} \right\}\\ = 160:40\\ = 4\end{array}\)
Tìm số nguyên \(x\), biết:
a) \(x - 10 = - 65\)
b) \(32:\left( {x + 125} \right) = - {4^2}\)
c) \(20 - 5\left( {2 - x} \right) = 45\)
a) Muốn tìm một số hạng trong một tổng ta lấy tổng trừ đi số hạng còn lại.
b) Áp dụng quy tắc chuyển vế để tìm x.
c) Áp dụng quy tắc chuyển vế để tìm x.
a) \(x - 10 = - 65\)
\(\begin{array}{l}x = - 65 + 10\\x = - 55\end{array}\)
Vậy \(x = - 55\)
b) \(32:\left( {x + 125} \right) = - {4^2}\)
\(\begin{array}{l}32:\left( {x + 125} \right) = - 16\\x + 125 = 32:\left( { - 16} \right)\\x + 125 = - 2\\x = - 2 - 125\\x = - 127\end{array}\)
Vậy \(x = - 127\)
c) \(20 - 5\left( {2 - x} \right) = 45\)
\(\begin{array}{l}5\left( {2 - x} \right) = 20 - 45\\5\left( {2 - x} \right) = - 25\\2 - x = - 25:5\\2 - x = - 5\\x = 2 - \left( { - 5} \right)\\x = 7\end{array}\)
Vậy \(x = 7\).
Một trường tổ chức cho học sinh đi học tập trải nghiệm. Ban tổ chức thấy rằng nếu xếp mỗi xe ô tô 36 học sinh; 40 học sinh hoặc 48 học sinh thì đều đủ chỗ, không thừa ai. Biết số học sinh của trường vào khoảng từ 1200 đến 1500 em. Hỏi trường đó có bao nhiêu học sinh?
Gọi số học sinh của trường là \(x\) (học sinh, \(x \in {\mathbb{N}^*},1200 \le x \le 1500\))
Lập luận \(x \in BC\left( {36;40;48} \right)\)
Phân tích 36; 40; 48 để tìm BCNN(36;40;48)
Kết hợp điều kiện của \(x\).
Gọi số học sinh của trường là \(x\) (học sinh, \(x \in {\mathbb{N}^*},1200 \le x \le 1500\))
Vì nếu xếp mỗi xe ô tô 36 học sinh; 40 học sinh hoặc 48 học sinh thì đều đủ chỗ nên \(x \vdots 36;x \vdots 40;x \vdots 48\), hay \(x \in BC\left( {36;40;48} \right)\).
Ta có: \(36 = {2^2}{.3^2}\)
\(40 = {2^3}.5\)
\(48 = {2^4}.3\)
Suy ra \(BCNN\left( {36;40;48} \right) = {2^4}{.3^2}.5 = 720\)
Do đó \(BC\left( {36;40;48} \right) = \left\{ {0;720;1440;2160;...} \right\}\)
Vì \(1200 \le x \le 1500\) nên \(x = 1440\) (TMĐK)
Vậy số học sinh của trường là 1440 học sinh.
Bác Khánh có mảnh vườn có hình dạng ghép bởi một hình chữ nhật và một hình thang. Kích thước của mảnh vườn được mô tả bằng bản vẽ hình sau.
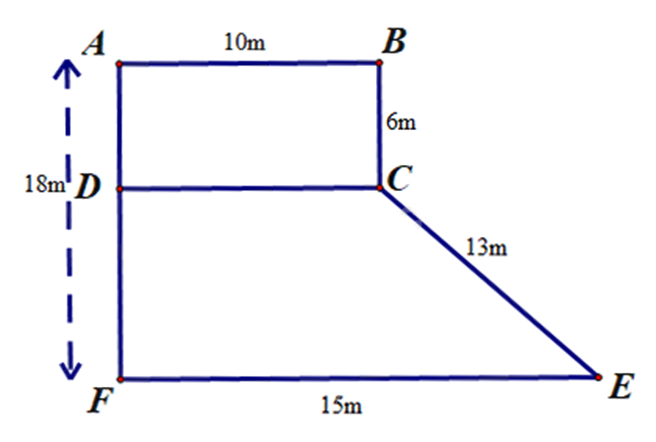
a) Tính diện tích phần vườn hình chữ nhật ABCD.
b) Bác Khánh muốn mua lưới mắt cáo để rào xung quanh mảnh vườn, tính chiều dài hàng rào?
c) Qua tìm hiểu Bác Khánh thấy người ta trồng ngô thì thu được 25 nghìn đồng/m\(^2\), trồng mía thì thu được 30 nghìn đồng/m\(^2\), trồng thanh long thì thu được 40 nghìn đồng/m\(^2\). Em hãy giúp Bác Khánh chọn phương án có doanh thu tốt hơn trong hai phương án sau:
+ Phương án 1: Trồng mía trên cả mảnh vườn
+ Phương án 2: Trồng ngô trên phần mảnh vườn hình thang và trồng thanh long trên mảnh vườn hình chữ nhật.
a) Áp dụng công thức tính diện tích phần vườn hình chữ nhật = chiều dài . chiều rộng.
b) Tính chu vi của mảnh vườn. Chiều dài hàng rào chính là chu vi của mảnh vườn.
c) Tính diện tích phần vườn hình thang = tổng hai đáy . chiều cao : 2.
Tính diện tích vườn bằng tổng diện tích phần vườn hình chữ nhật và phần vườn hình thang.
Phương án 1. Tính doanh thu khi trồng mía trên cả mảnh vườn.
Phương án 2. Tính doanh thu trồng ngô + doanh thu trồng thanh long.
Doanh thu = diện tích . số tiền thu được trên 1 mét vuông.
a) Diện tích phần vườn hình chữ nhật là: \(10.6 = 60\left( {{m^2}} \right)\)
b) Chiều dài hàng rào là: \(10 + 6 + 13 + 15 + 18 = 62\left( m \right)\)
c) Chiều cao phần vườn hình thang là: \(18 - 6 = 12\left( m \right)\)
Diện tích phần vườn hình thang là: \(\left( {10 + 15} \right).12:2 = 150\left( {{m^2}} \right)\)
Tổng diện tích mảnh vườn là: \(60 + 150 = 210\left( {{m^2}} \right)\)
- Doanh thu theo phương án 1 là: \(210.30 = 6300\) (nghìn đồng)
- Doanh thu theo phương án 2 là: \(25.150 + 40.60 = 6150\) (nghìn đồng)
Vậy bác Khánh chọn phương án 1 sẽ có doanh thu tốt hơn.
Chứng tỏ rằng với mọi \(n \in \mathbb{N}\) thì \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.
Hai số nguyên tố cùng nhau nếu ước chung lớn nhất của chúng bằng 1.
Giả sử ƯCLN(2n+1;3n+1) = d (d \( \in \mathbb{N}\)).
Chứng minh d = 1 nên \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.
Gọi ƯCLN(2n+1;3n+1) = d (d \( \in \mathbb{N}\)).
Suy ra \(2n + 1 \vdots d\); \(3n + 1 \vdots d\).
Do đó \(3\left( {2n + 1} \right) \vdots d\); \(2\left( {3n + 1} \right) \vdots d\)
hay \(6n + 3 \vdots d\); \(6n + 2 \vdots d\)
Suy ra \(\left( {6n + 3} \right) - \left( {6n + 2} \right) \vdots d\) hay \(1 \vdots d\) suy ra d \( \in \) Ư(1) = {1; -1}
Mà \(d \in \mathbb{N}\) nên d = 1.
Do đó ƯCLN(2n+1;3n+1) = 1
Vậy \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.
Đề thi học kì 1 Toán 6 - Đề số 17 là một bài kiểm tra đánh giá kiến thức và kỹ năng của học sinh sau nửa học kì đầu tiên của chương trình Toán 6. Đề thi thường bao gồm các chủ đề chính như:
Cấu trúc đề thi thường bao gồm các dạng bài tập khác nhau như trắc nghiệm, tự luận, bài tập thực tế. Tỷ lệ phân bổ điểm cho từng chủ đề có thể khác nhau tùy theo chương trình học của từng trường.
Bài tập trắc nghiệm thường kiểm tra khả năng hiểu và vận dụng kiến thức cơ bản của học sinh. Các câu hỏi trắc nghiệm thường yêu cầu học sinh chọn đáp án đúng trong số các đáp án cho sẵn. Để làm tốt dạng bài tập này, học sinh cần nắm vững các khái niệm, định nghĩa và tính chất của các đối tượng toán học.
Bài tập tự luận yêu cầu học sinh trình bày lời giải chi tiết cho từng bài toán. Để làm tốt dạng bài tập này, học sinh cần có khả năng phân tích bài toán, lựa chọn phương pháp giải phù hợp và trình bày lời giải một cách rõ ràng, logic.
Bài tập thực tế yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề trong thực tế cuộc sống. Dạng bài tập này giúp học sinh hiểu rõ hơn về ứng dụng của toán học trong thực tế và phát triển khả năng tư duy, sáng tạo.
Để giải tốt đề thi học kì 1 Toán 6 - Đề số 17, học sinh cần:
Ngoài việc luyện tập giải đề thi, học sinh có thể tham khảo các tài liệu ôn tập hữu ích sau:
Hãy dành thời gian ôn tập và luyện tập đầy đủ để chuẩn bị tốt nhất cho kỳ thi học kì 1 Toán 6. Chúc các em học sinh đạt kết quả tốt nhất!
Bài 1: Tính giá trị của biểu thức: 12 + 3 x 4 - 5
Lời giải:
12 + 3 x 4 - 5 = 12 + 12 - 5 = 24 - 5 = 19
| Chủ đề | Kiến thức trọng tâm |
|---|---|
| Số tự nhiên | Khái niệm, tính chất, các phép toán |
| Phân số | Khái niệm, so sánh, các phép toán |
| Số thập phân | Khái niệm, so sánh, các phép toán |