Chào mừng các em học sinh lớp 6 đến với đề thi giữa kì 1 Toán 6 - Đề số 5 của giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn tập và đánh giá kiến thức đã học trong giai đoạn đầu của năm học.
Với cấu trúc đề thi bám sát chương trình học và có đáp án chi tiết, các em có thể tự tin làm bài và kiểm tra kết quả của mình. Đây là cơ hội tuyệt vời để các em rèn luyện kỹ năng giải toán và chuẩn bị tốt nhất cho kỳ thi sắp tới.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. C | 2. C | 3. B | 4. A | 5. B | 6. C |
7. B | 8. B | 9. A | 10. D | 11. C | 12. B |
Câu 1
Phương pháp:
Vận dụng kiến thức về tập hợp số tự nhiên
Cách giải:
Tập hợp \(A\) gồm các số tự nhiên nhỏ hơn \(6\) là \(A = \left\{ {0;1;2;3;4;5} \right\}\)
Chọn C.
Câu 2
Phương pháp:
Vận dụng quy tắc nhân lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
Cách giải:
Ta có: \(8.8.8.8.8.8.8 = {8^1}{.8^1}{.8^1}{.8^1}{.8^1}{8^1}{.8^1} = {8^{1 + 1 + 1 + 1 + 1 + 1 + 1}} = {8^7}\)
Chọn C.
Câu 3
Phương pháp:
Vận dụng bài toán ngoặc để tìm \(x\): muốn tìm số hạng chưa biết của một tổng ta lấy tổng trừ đi số hạng đã biết.
Cách giải:
\(x + 189 = 249\)
\(\begin{array}{l}x = 249 - 189\\x = 60\end{array}\)
Vậy \(x = 60\)
Chọn B.
Câu 4
Phương pháp:
Vận dụng kiến thức về thứ tự thực hiện phép tính:
- Với biểu thức không có dấu ngoặc: Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ
- Với biểu thức có dấu ngoặc: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Cách giải:
\(\begin{array}{l}\,\,\,\,\,{5.2^3} + {3.2^2}\\ = 5.8 + 3.4\\ = 40 + 12\\ = 52\end{array}\)
Chọn A.
Câu 5
Phương pháp:
Vận dụng dấu hiệu chia hết cho\(2\) và dấu hiệu chia hết cho \(5\) để đưa ra kết luận.
Cách giải:
Số có chữ số tận cùng là \(0;2;4;6;8\) thì chia hết cho \(2\).
Số có chữ số tận cùng là \(0;5\) thì chia hết cho \(5\).
Vậy số có chữ số tận cùng là \(0\) thì chia hết cho cả \(2\) và \(5\).
Vậy số \(60\) là số thỏa mãn.
Chọn B.
Câu 6
Phương pháp:
Vận dụng dấu hiệu chia hết cho \(3\) và dấu hiệu chia hết cho \(9\).
Cách giải:
Ta có: \(3 + 2 = 5\) mà \(5\not \vdots 3;5\not \vdots 9\) nên \(32\not \vdots 3;32\not \vdots 9\) suy ra loại đáp án A.
Ta có: \(4 + 5 = 9\) mà \(9 \vdots 3;9 \vdots 9\) nên \(45 \vdots 3;45 \vdots 9\) suy ra loại đáp án B.
Ta có: \(1 + 5 = 6\) mà \(6 \vdots 3;6\not \vdots 9\) nên \(15 \vdots 3;15\not \vdots 9\) suy ra chọn đáp án C.
Ta có: \(5 + 4 = 9\) mà \(9 \vdots 3;9 \vdots 9\) nên \(54 \vdots 3;54 \vdots 9\) suy ra loại đáp án D.
Chọn C.
Câu 7
Phương pháp:
Vận dụng kiến thức về số nguyên tố: Số nguyên tố là số tự nhiên lớn hơn \(1\), chỉ có hai ước là \(1\) và chính nó.
Cách giải:
Ta có: \(13\) là số nguyên tố vì \(13 > 1\) và Ư\(\left( {13} \right) = \left\{ {1;13} \right\}\)
Chọn B.
Câu 8
Phương pháp:
Vận dụng cách tìm ước chung của hai số \(a\) và \(b\):
- Bước 1: Viết tập hợp các ước của \(a\) và ước của \(b\): Ư\(\left( a \right)\) và Ư\(\left( b \right)\)
- Bước 2: Tìm những phần tử chung của Ư\(\left( a \right)\) và Ư\(\left( b \right)\)
Cách giải:
Ta có: Ư\(\left( {30} \right) = \left\{ {1;2;3;5;6;10;15;30} \right\}\)
Ư\(\left( {48} \right) = \left\{ {1;2;3;4;6;8;12;16;24} \right\}\)
Do đó, ƯC\(\left( {30,48} \right) = \left\{ {1;2;3;6} \right\}\)
Vậy tập hợp ƯC\(\left( {30,48} \right)\) có \(4\) phần tử.
Chọn B.
Câu 9
Phương pháp:
Vận dụng quy tắc tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố:
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tô chung và riêng.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó.
Tích đó là BCNN phải tìm.
Cách giải:
Ta có: \(12 = {2^2}.3\)
\(\begin{array}{l}90 = {2.3^2}.5\\150 = {2.3.5^2}\end{array}\)
Suy ra BCNN\(\left( {12,90,150} \right) = {2^2}{.3^2}{.5^2} = 900\)
Chọn A.
Câu 10
Phương pháp:
Vận dụng đặc điểm của hình tam giác đều, hình vuông và hình thoi.
Cách giải:
Tam giác đều có \(3\) góc bằng nhau và bằng \({60^0}\) nên đáp án A sai.
Hình vuông là hình có \(4\) cạnh bằng nhau, \(4\) góc bằng nhau và bằng \({90^0}\) nên đáp án B sai.
Hình thoi có 2 đường chéo không bằng nhau nên đáp án C sai.
Hình vuông có \(2\) đường chéo bằng nhau nên đáp án D đúng nên chọn D.
Chọn D.
Câu 11
Phương pháp:
Vận dụng đặc điểm của hình vuông, hình chữ nhật, hình thoi và hình lục giác đều.
Cách giải:
Hình lục giác đều có \(3\) đường chéo chính bằng nhau nên đáp án A đúng.
Hình chữ nhật có 2 đường chéo bằng nhau nên đáp án B đúng.
Hình thoi có \(2\) đường chéo không bằng nhau nên đáp án C sai nên chọn C.
Hình vuông có \(2\) đường chéo bằng nhau nên đáp án D đúng.
Chọn C.
Câu 12
Phương pháp:
Vận dụng công thức tính diện tích hình thoi có độ dài hai đường chéo \(m\) và \(n\) là \(S = \dfrac{{m.n}}{2}\)
Cách giải:
Diện tích của hình thoi là: \(S = \dfrac{{40.30}}{2} = \dfrac{{1200}}{2} = 600{m^2}\)
Chọn B.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
Vận dụng cách tìm ước chung của hai số \(a\) và \(b\):
- Bước 1: Viết tập hợp các ước của \(a\) và ước của \(b\): Ư\(\left( a \right)\) và Ư\(\left( b \right)\)
- Bước 2: Tìm những phần tử chung của Ư\(\left( a \right)\) và Ư\(\left( b \right)\)
Cách giải:
Ta có: Ư\(\left( {12} \right) = \left\{ {1;2;3;4;6;12} \right\}\)
Ư\(\left( {36} \right) = \left\{ {1;2;3;4;6;9;12;18;36} \right\}\)
Ư\(\left( {60} \right) = \left\{ {1;2;3;4;5;6;10;12;15;60} \right\}\)
Do đó, ƯC\(\left( {12,36,60} \right) = \left\{ {1;2;3;4;6;12} \right\}\)
Vậy tập hợp ƯC\(\left( {12,36,60} \right)\) có \(6\) phần tử.
Bài 2
Phương pháp:
Vận dụng kiến thức về bội chung của hai hay nhiều số.
Cách giải:
Số tự nhiên \(x\) biết số đó vừa chia hết cho \(4\) và \(12\) nên \(x \in \)BC\(\left( {4,12} \right)\)
Ta có: \(4 = {2^2}\)
\(12 = {2^2}.3\)
Suy ra, BCNN\(\left( {4,12} \right) = {2^2}.3 = 12\)
Nên BC\(\left( {4,12} \right) = \left\{ {0;12;24;36;...} \right\}\)
Mà \(10 \le x \le 24\), suy ra \(x = 12\) hoặc \(x = 24\)
Bài 3
Phương pháp:
Vận dụng kiến thức về thứ tự thực hiện phép tính:
- Với biểu thức không có dấu ngoặc: Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ
- Với biểu thức có dấu ngoặc: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Cách giải:
a) \(9.\left[ {140 - {{\left( {15 - 5} \right)}^2}} \right]\) \(\begin{array}{l} = 9.\left( {140 - {{10}^2}} \right)\\ = 9.\left( {140 - 100} \right)\\ = 9.40\\ = 360\end{array}\) | b) \(53.205 + 46.205 + 205\) \(\begin{array}{l} = 205.\left( {53 + 46 + 1} \right)\\ = 205.100\\ = 20500\end{array}\) |
Bài 4
Phương pháp:
Giải bài toán ngược để tìm \(x\)
Cách giải:
a) \(7 + 2\left( {x - 3} \right) = 11\) \(\begin{array}{l}2\left( {x - 3} \right) = 11 - 7\\2\left( {x - 3} \right) = 4\\x - 3 = 4:2\\x - 3 = 2\\x = 2 + 3\\x = 5\end{array}\) Vậy \(x = 5\). | b) \({\left( {x + 2} \right)^3} + {4.3^2} = 63\) \(\begin{array}{l}{\left( {x + 2} \right)^3} + 4.9 = 63\\{\left( {x + 2} \right)^3} + 36 = 63\\{\left( {x + 2} \right)^3} = 63 - 36\\{\left( {x + 2} \right)^3} = 27\\{\left( {x + 2} \right)^3} = {3^3}\\x + 2 = 3\\x = 3 - 2\\x = 1\end{array}\) Vậy \(x = 1\). |
Bài 5
Phương pháp:
Biến đổi \(46 < 2x + 4 < 100 \Rightarrow 21 < x < 48\).
Liệt kê các phần tử của \(x\) thỏa mãn.
Cách giải:
Ta có: \(46 < 2x + 4 < 100\)
\(\begin{array}{l} \Rightarrow 42 < 2x < 96\\ \Rightarrow 21 < x < 48\end{array}\)
Mà \(x\) là số tự nhiên nên \(x \in \left\{ {22;\,\,23;\,\, \ldots ;\,\,47;\,\,48} \right\}\).
\( \Rightarrow \) Có \(\left( {48 - 22} \right):1 + 1 = 27\) (số) thỏa mãn.
Vậy có tất cả \(27\) số tự nhiên \(x\) thỏa mãn đề bài.
Bài 6
Phương pháp:
Tính diện tích phần vườn hình thang cân
Tính diện tích phần mảnh vườn hình chữ nhật
Tính diện tích của cả mảnh vườn
Tính số tiền bác An phải chi trả.
Cách giải:
Diện tích phần mảnh vườn hình thang cân là: \(\dfrac{{\left( {5 + 7} \right).2}}{2} = 12\left( {{m^2}} \right)\)
Diện tích phần mảnh vườn hình chữ nhật là: \(6.7 = 42\left( {{m^2}} \right)\)
Diện tích của mảnh vườn là: \(12 + 42 = 54\left( {{m^2}} \right)\)
Số tiền bác An phải chi trả để trải kín cỏ là: \(8000.54 = 432000\) (đồng)
Bài 7
Phương pháp:
Nhóm các số hạng hợp lí với nhau, tính lũy thừa của một cơ số, tính tổng.
Cách giải:
Ta có: \(S = 1 + {5^2} + {5^4} + ... + {5^{2020}}\)
\(\begin{array}{l} = \left( {1 + {5^4}} \right) + \left( {{5^2} + {5^6}} \right) + ... + \left( {{5^{2016}} + {5^{2020}}} \right)\\ = \left( {1 + {5^4}} \right) + {5^2}.\left( {1 + {5^4}} \right) + ... + {5^{2016}}.\left( {1 + {5^4}} \right)\\ = \left( {1 + {5^4}} \right).\left( {1 + {5^2} + ... + {5^{2016}}} \right)\\ = 626.\left( {1 + {5^2} + ... + {5^{2016}}} \right)\end{array}\)
Mà \(626 \vdots 313\) nên \(S \vdots 313\)
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Cho tập hợp \(A\) gồm các số tự nhiên nhỏ hơn \(6\), trong các cách viết sau, cách viết nào đúng?
A. \(A = \left\{ {0;1;2;3;4;5;6} \right\}\)
B. \(A = \left\{ {1;2;3;4;5;6} \right\}\)
C. \(A = \left\{ {0;1;2;3;4;5} \right\}\)
D.\(A = \left\{ {1;2;3;4;5} \right\}\)
Câu 2. Tích \(8.8.8.8.8.8.8\) được viết gọn bằng cách dùng lũy thừa là:
A. \(7.8\)
B. \({7^8}\)
C. \({8^7}\)
D. \({8^8}\)
Câu 3. Tìm \(x\) biết: \(x + 189 = 249\)
A. \(x = 438\)
B. \(x = 60\)
C. \(x = 50\)
D. \(x = 328\)
Câu 4. Kết quả của phép tính: \({5.2^3} + {3.2^2}\) là:
A. \(52\)
B. \(16\)
C. \(61\)
D. \(6\)
Câu 5. Số nào sau đây chia hết cho cả \(2\) và \(5\)?
A. \(38\)
B. \(60\)
C. \(75\)
D. \(21\)
Câu 6. Số nào sau đây chia hết cho \(3\) nhưng không chia hết cho \(9\)?
A. \(32\)
B. \(45\)
C. \(15\)
D. \(54\)
Câu 7. Số nào sau đây là số nguyên tố?
A. \(1\)
B. \(13\)
C. \(21\)
D. \(51\)
Câu 8. Tập hợp ước chung của \(30\) và \(48\) có bao nhiêu phần tử?
A. \(3\)
B. \(4\)
C. \(5\)
D. \(6\)
Câu 9. Tìm BCNN của \(12;90\) và \(150\).
A. \(900\)
B. \(150\)
C. \(600\)
D. \(720\)
Câu 10. Trong các phát biểu sau, phát biểu nào đúng?
A. Tam giác đều có \(3\) góc bằng nhau và bằng \({90^0}\).
B. Hình vuông là hình có \(4\) cạnh bằng nhau, \(4\) góc bằng nhau và bằng \({60^0}\).
C. Hình thoi có \(2\) đường chéo bằng nhau.
D. Hình vuông có \(2\) đường chéo bằng nhau.
Câu 11. Trong các phát biểu sau, phát biểu nào không đúng?
A. Hình lục giác đều có \(3\) đường chéo chính bằng nhau.
B. Hình chữ nhật có 2 đường chéo bằng nhau.
C. Hình thoi có \(2\) đường chéo bằng nhau.
D. Hình vuông có \(2\) đường chéo bằng nhau.
Câu 12. Diện tích hình thoi có hai đường chéo là \(40m\) và \(30m\) là:
A. \(1200{m^2}\)
B. \(600{m^2}\)
C. \(70m\)
D. \(120{m^2}\)
Phần II. Tự luận (7 điểm):
Bài 1. (1 điểm) Tập hợp ước chung của các số \(12;36;60\) gồm bao nhiêu phần tử
Bài 2. (1 điểm) Tìm số tự nhiên \(x\) biết số đó vừa chia hết cho \(4\) và \(12\), biết \(10 \le x \le 24\)
Bài 3. (1 điểm) Thực hiện phép tính:
a) \(9.\left[ {140 - {{\left( {15 - 5} \right)}^2}} \right]\)
b) \(53.205 + 46.205 + 205\)
Bài 4. (1 điểm) Tìm \(x\) biết:
a) \(7 + 2\left( {x - 3} \right) = 11\)
b) \({\left( {x + 2} \right)^3} + {4.3^2} = 63\)
Bài 5. (1 điểm) Có bao nhiêu số tự nhiên \(x\) thỏa mãn \(46 < 2x + 4 < 100\)?
Bài 6. (1 điểm) Mảnh vườn nhà bác An có kích thước như hình vẽ bên:
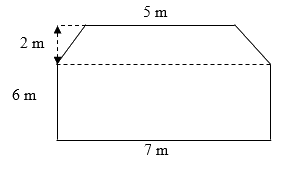
Tính số tiền mà bác An phải trả khi trải kín cỏ cho mảnh vườn biết mỗi mét vuông cỏ có giá là \(8000\) đồng.
Bài 7. (1 điểm) Cho \(S = 1 + {5^2} + {5^4} + ... + {5^{2020}}\). Chứng minh rằng \(S\) chia hết cho \(313\).
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Cho tập hợp \(A\) gồm các số tự nhiên nhỏ hơn \(6\), trong các cách viết sau, cách viết nào đúng?
A. \(A = \left\{ {0;1;2;3;4;5;6} \right\}\)
B. \(A = \left\{ {1;2;3;4;5;6} \right\}\)
C. \(A = \left\{ {0;1;2;3;4;5} \right\}\)
D.\(A = \left\{ {1;2;3;4;5} \right\}\)
Câu 2. Tích \(8.8.8.8.8.8.8\) được viết gọn bằng cách dùng lũy thừa là:
A. \(7.8\)
B. \({7^8}\)
C. \({8^7}\)
D. \({8^8}\)
Câu 3. Tìm \(x\) biết: \(x + 189 = 249\)
A. \(x = 438\)
B. \(x = 60\)
C. \(x = 50\)
D. \(x = 328\)
Câu 4. Kết quả của phép tính: \({5.2^3} + {3.2^2}\) là:
A. \(52\)
B. \(16\)
C. \(61\)
D. \(6\)
Câu 5. Số nào sau đây chia hết cho cả \(2\) và \(5\)?
A. \(38\)
B. \(60\)
C. \(75\)
D. \(21\)
Câu 6. Số nào sau đây chia hết cho \(3\) nhưng không chia hết cho \(9\)?
A. \(32\)
B. \(45\)
C. \(15\)
D. \(54\)
Câu 7. Số nào sau đây là số nguyên tố?
A. \(1\)
B. \(13\)
C. \(21\)
D. \(51\)
Câu 8. Tập hợp ước chung của \(30\) và \(48\) có bao nhiêu phần tử?
A. \(3\)
B. \(4\)
C. \(5\)
D. \(6\)
Câu 9. Tìm BCNN của \(12;90\) và \(150\).
A. \(900\)
B. \(150\)
C. \(600\)
D. \(720\)
Câu 10. Trong các phát biểu sau, phát biểu nào đúng?
A. Tam giác đều có \(3\) góc bằng nhau và bằng \({90^0}\).
B. Hình vuông là hình có \(4\) cạnh bằng nhau, \(4\) góc bằng nhau và bằng \({60^0}\).
C. Hình thoi có \(2\) đường chéo bằng nhau.
D. Hình vuông có \(2\) đường chéo bằng nhau.
Câu 11. Trong các phát biểu sau, phát biểu nào không đúng?
A. Hình lục giác đều có \(3\) đường chéo chính bằng nhau.
B. Hình chữ nhật có 2 đường chéo bằng nhau.
C. Hình thoi có \(2\) đường chéo bằng nhau.
D. Hình vuông có \(2\) đường chéo bằng nhau.
Câu 12. Diện tích hình thoi có hai đường chéo là \(40m\) và \(30m\) là:
A. \(1200{m^2}\)
B. \(600{m^2}\)
C. \(70m\)
D. \(120{m^2}\)
Phần II. Tự luận (7 điểm):
Bài 1. (1 điểm) Tập hợp ước chung của các số \(12;36;60\) gồm bao nhiêu phần tử
Bài 2. (1 điểm) Tìm số tự nhiên \(x\) biết số đó vừa chia hết cho \(4\) và \(12\), biết \(10 \le x \le 24\)
Bài 3. (1 điểm) Thực hiện phép tính:
a) \(9.\left[ {140 - {{\left( {15 - 5} \right)}^2}} \right]\)
b) \(53.205 + 46.205 + 205\)
Bài 4. (1 điểm) Tìm \(x\) biết:
a) \(7 + 2\left( {x - 3} \right) = 11\)
b) \({\left( {x + 2} \right)^3} + {4.3^2} = 63\)
Bài 5. (1 điểm) Có bao nhiêu số tự nhiên \(x\) thỏa mãn \(46 < 2x + 4 < 100\)?
Bài 6. (1 điểm) Mảnh vườn nhà bác An có kích thước như hình vẽ bên:
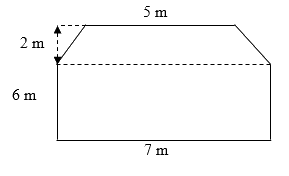
Tính số tiền mà bác An phải trả khi trải kín cỏ cho mảnh vườn biết mỗi mét vuông cỏ có giá là \(8000\) đồng.
Bài 7. (1 điểm) Cho \(S = 1 + {5^2} + {5^4} + ... + {5^{2020}}\). Chứng minh rằng \(S\) chia hết cho \(313\).
Phần I: Trắc nghiệm
1. C | 2. C | 3. B | 4. A | 5. B | 6. C |
7. B | 8. B | 9. A | 10. D | 11. C | 12. B |
Câu 1
Phương pháp:
Vận dụng kiến thức về tập hợp số tự nhiên
Cách giải:
Tập hợp \(A\) gồm các số tự nhiên nhỏ hơn \(6\) là \(A = \left\{ {0;1;2;3;4;5} \right\}\)
Chọn C.
Câu 2
Phương pháp:
Vận dụng quy tắc nhân lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
Cách giải:
Ta có: \(8.8.8.8.8.8.8 = {8^1}{.8^1}{.8^1}{.8^1}{.8^1}{8^1}{.8^1} = {8^{1 + 1 + 1 + 1 + 1 + 1 + 1}} = {8^7}\)
Chọn C.
Câu 3
Phương pháp:
Vận dụng bài toán ngoặc để tìm \(x\): muốn tìm số hạng chưa biết của một tổng ta lấy tổng trừ đi số hạng đã biết.
Cách giải:
\(x + 189 = 249\)
\(\begin{array}{l}x = 249 - 189\\x = 60\end{array}\)
Vậy \(x = 60\)
Chọn B.
Câu 4
Phương pháp:
Vận dụng kiến thức về thứ tự thực hiện phép tính:
- Với biểu thức không có dấu ngoặc: Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ
- Với biểu thức có dấu ngoặc: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Cách giải:
\(\begin{array}{l}\,\,\,\,\,{5.2^3} + {3.2^2}\\ = 5.8 + 3.4\\ = 40 + 12\\ = 52\end{array}\)
Chọn A.
Câu 5
Phương pháp:
Vận dụng dấu hiệu chia hết cho\(2\) và dấu hiệu chia hết cho \(5\) để đưa ra kết luận.
Cách giải:
Số có chữ số tận cùng là \(0;2;4;6;8\) thì chia hết cho \(2\).
Số có chữ số tận cùng là \(0;5\) thì chia hết cho \(5\).
Vậy số có chữ số tận cùng là \(0\) thì chia hết cho cả \(2\) và \(5\).
Vậy số \(60\) là số thỏa mãn.
Chọn B.
Câu 6
Phương pháp:
Vận dụng dấu hiệu chia hết cho \(3\) và dấu hiệu chia hết cho \(9\).
Cách giải:
Ta có: \(3 + 2 = 5\) mà \(5\not \vdots 3;5\not \vdots 9\) nên \(32\not \vdots 3;32\not \vdots 9\) suy ra loại đáp án A.
Ta có: \(4 + 5 = 9\) mà \(9 \vdots 3;9 \vdots 9\) nên \(45 \vdots 3;45 \vdots 9\) suy ra loại đáp án B.
Ta có: \(1 + 5 = 6\) mà \(6 \vdots 3;6\not \vdots 9\) nên \(15 \vdots 3;15\not \vdots 9\) suy ra chọn đáp án C.
Ta có: \(5 + 4 = 9\) mà \(9 \vdots 3;9 \vdots 9\) nên \(54 \vdots 3;54 \vdots 9\) suy ra loại đáp án D.
Chọn C.
Câu 7
Phương pháp:
Vận dụng kiến thức về số nguyên tố: Số nguyên tố là số tự nhiên lớn hơn \(1\), chỉ có hai ước là \(1\) và chính nó.
Cách giải:
Ta có: \(13\) là số nguyên tố vì \(13 > 1\) và Ư\(\left( {13} \right) = \left\{ {1;13} \right\}\)
Chọn B.
Câu 8
Phương pháp:
Vận dụng cách tìm ước chung của hai số \(a\) và \(b\):
- Bước 1: Viết tập hợp các ước của \(a\) và ước của \(b\): Ư\(\left( a \right)\) và Ư\(\left( b \right)\)
- Bước 2: Tìm những phần tử chung của Ư\(\left( a \right)\) và Ư\(\left( b \right)\)
Cách giải:
Ta có: Ư\(\left( {30} \right) = \left\{ {1;2;3;5;6;10;15;30} \right\}\)
Ư\(\left( {48} \right) = \left\{ {1;2;3;4;6;8;12;16;24} \right\}\)
Do đó, ƯC\(\left( {30,48} \right) = \left\{ {1;2;3;6} \right\}\)
Vậy tập hợp ƯC\(\left( {30,48} \right)\) có \(4\) phần tử.
Chọn B.
Câu 9
Phương pháp:
Vận dụng quy tắc tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố:
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tô chung và riêng.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó.
Tích đó là BCNN phải tìm.
Cách giải:
Ta có: \(12 = {2^2}.3\)
\(\begin{array}{l}90 = {2.3^2}.5\\150 = {2.3.5^2}\end{array}\)
Suy ra BCNN\(\left( {12,90,150} \right) = {2^2}{.3^2}{.5^2} = 900\)
Chọn A.
Câu 10
Phương pháp:
Vận dụng đặc điểm của hình tam giác đều, hình vuông và hình thoi.
Cách giải:
Tam giác đều có \(3\) góc bằng nhau và bằng \({60^0}\) nên đáp án A sai.
Hình vuông là hình có \(4\) cạnh bằng nhau, \(4\) góc bằng nhau và bằng \({90^0}\) nên đáp án B sai.
Hình thoi có 2 đường chéo không bằng nhau nên đáp án C sai.
Hình vuông có \(2\) đường chéo bằng nhau nên đáp án D đúng nên chọn D.
Chọn D.
Câu 11
Phương pháp:
Vận dụng đặc điểm của hình vuông, hình chữ nhật, hình thoi và hình lục giác đều.
Cách giải:
Hình lục giác đều có \(3\) đường chéo chính bằng nhau nên đáp án A đúng.
Hình chữ nhật có 2 đường chéo bằng nhau nên đáp án B đúng.
Hình thoi có \(2\) đường chéo không bằng nhau nên đáp án C sai nên chọn C.
Hình vuông có \(2\) đường chéo bằng nhau nên đáp án D đúng.
Chọn C.
Câu 12
Phương pháp:
Vận dụng công thức tính diện tích hình thoi có độ dài hai đường chéo \(m\) và \(n\) là \(S = \dfrac{{m.n}}{2}\)
Cách giải:
Diện tích của hình thoi là: \(S = \dfrac{{40.30}}{2} = \dfrac{{1200}}{2} = 600{m^2}\)
Chọn B.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
Vận dụng cách tìm ước chung của hai số \(a\) và \(b\):
- Bước 1: Viết tập hợp các ước của \(a\) và ước của \(b\): Ư\(\left( a \right)\) và Ư\(\left( b \right)\)
- Bước 2: Tìm những phần tử chung của Ư\(\left( a \right)\) và Ư\(\left( b \right)\)
Cách giải:
Ta có: Ư\(\left( {12} \right) = \left\{ {1;2;3;4;6;12} \right\}\)
Ư\(\left( {36} \right) = \left\{ {1;2;3;4;6;9;12;18;36} \right\}\)
Ư\(\left( {60} \right) = \left\{ {1;2;3;4;5;6;10;12;15;60} \right\}\)
Do đó, ƯC\(\left( {12,36,60} \right) = \left\{ {1;2;3;4;6;12} \right\}\)
Vậy tập hợp ƯC\(\left( {12,36,60} \right)\) có \(6\) phần tử.
Bài 2
Phương pháp:
Vận dụng kiến thức về bội chung của hai hay nhiều số.
Cách giải:
Số tự nhiên \(x\) biết số đó vừa chia hết cho \(4\) và \(12\) nên \(x \in \)BC\(\left( {4,12} \right)\)
Ta có: \(4 = {2^2}\)
\(12 = {2^2}.3\)
Suy ra, BCNN\(\left( {4,12} \right) = {2^2}.3 = 12\)
Nên BC\(\left( {4,12} \right) = \left\{ {0;12;24;36;...} \right\}\)
Mà \(10 \le x \le 24\), suy ra \(x = 12\) hoặc \(x = 24\)
Bài 3
Phương pháp:
Vận dụng kiến thức về thứ tự thực hiện phép tính:
- Với biểu thức không có dấu ngoặc: Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ
- Với biểu thức có dấu ngoặc: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Cách giải:
a) \(9.\left[ {140 - {{\left( {15 - 5} \right)}^2}} \right]\) \(\begin{array}{l} = 9.\left( {140 - {{10}^2}} \right)\\ = 9.\left( {140 - 100} \right)\\ = 9.40\\ = 360\end{array}\) | b) \(53.205 + 46.205 + 205\) \(\begin{array}{l} = 205.\left( {53 + 46 + 1} \right)\\ = 205.100\\ = 20500\end{array}\) |
Bài 4
Phương pháp:
Giải bài toán ngược để tìm \(x\)
Cách giải:
a) \(7 + 2\left( {x - 3} \right) = 11\) \(\begin{array}{l}2\left( {x - 3} \right) = 11 - 7\\2\left( {x - 3} \right) = 4\\x - 3 = 4:2\\x - 3 = 2\\x = 2 + 3\\x = 5\end{array}\) Vậy \(x = 5\). | b) \({\left( {x + 2} \right)^3} + {4.3^2} = 63\) \(\begin{array}{l}{\left( {x + 2} \right)^3} + 4.9 = 63\\{\left( {x + 2} \right)^3} + 36 = 63\\{\left( {x + 2} \right)^3} = 63 - 36\\{\left( {x + 2} \right)^3} = 27\\{\left( {x + 2} \right)^3} = {3^3}\\x + 2 = 3\\x = 3 - 2\\x = 1\end{array}\) Vậy \(x = 1\). |
Bài 5
Phương pháp:
Biến đổi \(46 < 2x + 4 < 100 \Rightarrow 21 < x < 48\).
Liệt kê các phần tử của \(x\) thỏa mãn.
Cách giải:
Ta có: \(46 < 2x + 4 < 100\)
\(\begin{array}{l} \Rightarrow 42 < 2x < 96\\ \Rightarrow 21 < x < 48\end{array}\)
Mà \(x\) là số tự nhiên nên \(x \in \left\{ {22;\,\,23;\,\, \ldots ;\,\,47;\,\,48} \right\}\).
\( \Rightarrow \) Có \(\left( {48 - 22} \right):1 + 1 = 27\) (số) thỏa mãn.
Vậy có tất cả \(27\) số tự nhiên \(x\) thỏa mãn đề bài.
Bài 6
Phương pháp:
Tính diện tích phần vườn hình thang cân
Tính diện tích phần mảnh vườn hình chữ nhật
Tính diện tích của cả mảnh vườn
Tính số tiền bác An phải chi trả.
Cách giải:
Diện tích phần mảnh vườn hình thang cân là: \(\dfrac{{\left( {5 + 7} \right).2}}{2} = 12\left( {{m^2}} \right)\)
Diện tích phần mảnh vườn hình chữ nhật là: \(6.7 = 42\left( {{m^2}} \right)\)
Diện tích của mảnh vườn là: \(12 + 42 = 54\left( {{m^2}} \right)\)
Số tiền bác An phải chi trả để trải kín cỏ là: \(8000.54 = 432000\) (đồng)
Bài 7
Phương pháp:
Nhóm các số hạng hợp lí với nhau, tính lũy thừa của một cơ số, tính tổng.
Cách giải:
Ta có: \(S = 1 + {5^2} + {5^4} + ... + {5^{2020}}\)
\(\begin{array}{l} = \left( {1 + {5^4}} \right) + \left( {{5^2} + {5^6}} \right) + ... + \left( {{5^{2016}} + {5^{2020}}} \right)\\ = \left( {1 + {5^4}} \right) + {5^2}.\left( {1 + {5^4}} \right) + ... + {5^{2016}}.\left( {1 + {5^4}} \right)\\ = \left( {1 + {5^4}} \right).\left( {1 + {5^2} + ... + {5^{2016}}} \right)\\ = 626.\left( {1 + {5^2} + ... + {5^{2016}}} \right)\end{array}\)
Mà \(626 \vdots 313\) nên \(S \vdots 313\)
Đề thi giữa kì 1 Toán 6 - Đề số 5 là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức cơ bản của học sinh sau một nửa học kỳ đầu tiên. Đề thi thường bao gồm các dạng bài tập thuộc các chủ đề chính đã được học, như:
Cấu trúc đề thi thường bao gồm các câu hỏi trắc nghiệm, câu hỏi tự luận ngắn và các bài toán giải chi tiết. Thời gian làm bài thường là 60-90 phút.
Việc luyện tập với đề thi giữa kì 1 Toán 6 - Đề số 5 mang lại nhiều lợi ích cho học sinh:
Để đạt kết quả tốt nhất trong kỳ thi, học sinh cần có phương pháp giải bài tập hiệu quả. Dưới đây là một số lời khuyên:
Bài toán: Tính giá trị của biểu thức sau: (12 + 6) : 3 - 2 x 4
Giải:
Ngoài việc luyện tập với đề thi giữa kì 1 Toán 6 - Đề số 5, học sinh có thể tham khảo thêm các tài liệu sau:
Hãy dành thời gian ôn tập và luyện tập thường xuyên để nắm vững kiến thức và tự tin bước vào kỳ thi giữa kì 1 Toán 6. Chúc các em học sinh đạt kết quả tốt nhất!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Số tự nhiên | Cao |
| Phân số | Trung bình |
| Số thập phân | Trung bình |
| Hình học | Thấp |