Chào mừng các em học sinh lớp 6 đến với đề thi học kì 2 môn Toán số 6 của giaitoan.edu.vn.
Đề thi này được biên soạn theo chuẩn kiến thức và kỹ năng của chương trình Toán 6, giúp các em làm quen với cấu trúc đề thi và rèn luyện khả năng giải quyết các bài toán thực tế.
Cùng giaitoan.edu.vn ôn tập và tự tin bước vào kỳ thi học kì 2 sắp tới!
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Sắp xếp các số sau theo thứ tự từ bé đến lớn: - 2,064; - 2,604; - 2,406; - 2,046.
A. - 2,604; - 2,406; - 2,064; - 2,046
B. - 2,604; - 2,064; - 2,406; - 2,046
C. - 2,046; - 2,064; - 2,406; - 2,604
D. - 2,604; - 2,406; - 2,046; - 2,064
Câu 2. Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng kích thước, khối lượng như nhau. Mỗi lần Hà lấy ngẫu nhiên 1 quả bóng trong hộp, ghi lại màu của quả bóng đó và bỏ lại quả bóng đó vào hộp. Bạn Hà lấy 15 lần liên tiếp, có 5 lần xuất hiện màu vàng thì xác suất thực nghiệm xuất hiện màu vàng bằng bao nhiêu?
A. \(\dfrac{1}{3}\)
B. \(\dfrac{1}{4}\)
C. \(\dfrac{2}{5}\)
D. \(\dfrac{1}{5}\)
Câu 3. \(\dfrac{2}{5}\) của x bằng 20. Giá trị của x là:
A. 50
B. 8
C. 10
D. 5
Câu 4. Kim phút và kim giờ của đồng hồ tạo thành góc bẹt tại thời điểm:
A. 12 giờ
B. 6 giờ 30 phút
C. 15 giờ
D. 6 giờ
Phần II. Tự luận (8 điểm):
Bài 1 (2,0 điểm) Thực hiện phép tính (tính hợp lý nếu có thể)
a) \(\dfrac{1}{6} + \dfrac{{ - 5}}{3}\)
b) \(\left( {2022,19 + 152,3} \right) - \left( {2022,19 - 7,7} \right)\)
c) \(\dfrac{{ - 7}}{9}.\dfrac{3}{{11}} + \dfrac{{ - 7}}{{11}}:\dfrac{9}{8} + 5\dfrac{7}{9}\)
Bài 2 (2,0 điểm) Tìm x biết:
a) \(x - \dfrac{1}{2} = \dfrac{{ - 2}}{3}\)
b) \(\dfrac{2}{3}:x = 1,4 - \dfrac{{12}}{5}\)
c) \({\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2} + \dfrac{5}{9} = {2022^0}\)
Bài 3 (1,5 điểm) Lớp 6A có 48 học sinh gồm ba loại giỏi, khá và trung bình, trong đó số học sinh giỏi chiếm 25% số học sinh cả lớp, số học sinh khá bằng \(1\dfrac{1}{3}\), số học sinh giỏi, còn lại là học sinh trung bình.
a) Tính số học sinh mỗi loại của lớp 6A?
b) Tính tỉ số phần trăm giữa số học sinh trung bình với số học sinh cả lớp? (làm tròn đến chữ số thập phân thứ hai).
Bài 4 (2,0 điểm) Cho đường thẳng xy. Trên đường thẳng xy lấy điểm O. Vẽ điểm A thuộc tia Ox sao cho OA = 4cm, điểm B thuộc tia Oy sao cho OB = 2cm.
a) Viết các trường hợp hai tia đối nhau gốc A, hai tia trùng nhau gốc B.
b) Tính AB.
c) Gọi I là trung điểm của đoạn thẳng OA. Điểm O có là trung điểm của đoạn thẳng IB không? Vì sao?
Bài 5 (0,5 điểm) Tìm số tự nhiên n để phân số \(B{\rm{ }} = \dfrac{{10n - 3}}{{4n - 10}}\) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.
Tải về
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Sắp xếp các số sau theo thứ tự từ bé đến lớn: - 2,064; - 2,604; - 2,406; - 2,046.
A. - 2,604; - 2,406; - 2,064; - 2,046
B. - 2,604; - 2,064; - 2,406; - 2,046
C. - 2,046; - 2,064; - 2,406; - 2,604
D. - 2,604; - 2,406; - 2,046; - 2,064
Câu 2. Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng kích thước, khối lượng như nhau. Mỗi lần Hà lấy ngẫu nhiên 1 quả bóng trong hộp, ghi lại màu của quả bóng đó và bỏ lại quả bóng đó vào hộp. Bạn Hà lấy 15 lần liên tiếp, có 5 lần xuất hiện màu vàng thì xác suất thực nghiệm xuất hiện màu vàng bằng bao nhiêu?
A. \(\dfrac{1}{3}\)
B. \(\dfrac{1}{4}\)
C. \(\dfrac{2}{5}\)
D. \(\dfrac{1}{5}\)
Câu 3. \(\dfrac{2}{5}\) của x bằng 20. Giá trị của x là:
A. 50
B. 8
C. 10
D. 5
Câu 4. Kim phút và kim giờ của đồng hồ tạo thành góc bẹt tại thời điểm:
A. 12 giờ
B. 6 giờ 30 phút
C. 15 giờ
D. 6 giờ
Phần II. Tự luận (8 điểm):
Bài 1 (2,0 điểm) Thực hiện phép tính (tính hợp lý nếu có thể)
a) \(\dfrac{1}{6} + \dfrac{{ - 5}}{3}\)
b) \(\left( {2022,19 + 152,3} \right) - \left( {2022,19 - 7,7} \right)\)
c) \(\dfrac{{ - 7}}{9}.\dfrac{3}{{11}} + \dfrac{{ - 7}}{{11}}:\dfrac{9}{8} + 5\dfrac{7}{9}\)
Bài 2 (2,0 điểm) Tìm x biết:
a) \(x - \dfrac{1}{2} = \dfrac{{ - 2}}{3}\)
b) \(\dfrac{2}{3}:x = 1,4 - \dfrac{{12}}{5}\)
c) \({\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2} + \dfrac{5}{9} = {2022^0}\)
Bài 3 (1,5 điểm) Lớp 6A có 48 học sinh gồm ba loại giỏi, khá và trung bình, trong đó số học sinh giỏi chiếm 25% số học sinh cả lớp, số học sinh khá bằng \(1\dfrac{1}{3}\), số học sinh giỏi, còn lại là học sinh trung bình.
a) Tính số học sinh mỗi loại của lớp 6A?
b) Tính tỉ số phần trăm giữa số học sinh trung bình với số học sinh cả lớp? (làm tròn đến chữ số thập phân thứ hai).
Bài 4 (2,0 điểm) Cho đường thẳng xy. Trên đường thẳng xy lấy điểm O. Vẽ điểm A thuộc tia Ox sao cho OA = 4cm, điểm B thuộc tia Oy sao cho OB = 2cm.
a) Viết các trường hợp hai tia đối nhau gốc A, hai tia trùng nhau gốc B.
b) Tính AB.
c) Gọi I là trung điểm của đoạn thẳng OA. Điểm O có là trung điểm của đoạn thẳng IB không? Vì sao?
Bài 5 (0,5 điểm) Tìm số tự nhiên n để phân số \(B{\rm{ }} = \dfrac{{10n - 3}}{{4n - 10}}\) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.
Phần I: Trắc nghiệm
1. A | 2. A | 3. A | 4. D |
Câu 1
Phương pháp:
So sánh và sắp xếp theo thứ tự từ bé đến lớn.
Cách giải:
Các số xếp theo thứ tự từ bé đến lớn là: - 2,604; - 2,406; - 2,064; - 2,046
Chọn A.
Câu 2
Phương pháp:
Xác suất thực nghiệm xuất hiện màu vàng = Số lần xuất hiện màu vàng : Số lần thử
Cách giải:
Xác suất thực nghiệm xuất hiện màu vàng là: \(\dfrac{5}{{15}} = \dfrac{1}{3}\)
Chọn A.
Câu 3
Phương pháp:
Lấy giá trị chia cho phân số tương ứng.
Cách giải:
\(\begin{array}{l}\dfrac{2}{5}.x = 20\\\,\,\,\,\,x = 20:\dfrac{2}{5}\\\,\,\,\,\,x = 50\end{array}\)
Chọn A.
Câu 4
Phương pháp:
Kim phút và kim giờ của đồng hồ tạo thành góc bẹt tại thời điểm 6 giờ.
Cách giải:
Kim phút và kim giờ của đồng hồ tạo thành góc bẹt tại thời điểm 6 giờ.
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp
a) Thực hiện phép cộng hai phân số.
b) Nhóm thích hợp.
c) Sử dụng tính chất phân phối của phép nhân với phép cộng.
Cách giải:
a) \(\dfrac{1}{6} + \dfrac{{ - 5}}{3} = \dfrac{1}{6} + \dfrac{{ - 10}}{6} = \dfrac{{ - 9}}{6} = \dfrac{{ - 3}}{2}\)
b)
\(\begin{array}{l}\left( {2022,19 + 152,3} \right) - \left( {2022,19 - 7,7} \right)\\ = 2022,19 + 152,3 - 2022,19 + 7,7\\ = \left( {2022,19 - 2022,19} \right) + \left( {152,3 + 7,7} \right)\\ = 0 + 160 = 160\end{array}\)
c)
\(\begin{array}{l}\dfrac{{ - 7}}{9}.\dfrac{3}{{11}} + \dfrac{{ - 7}}{{11}}:\dfrac{9}{8} + 5\dfrac{7}{9}\\ = \dfrac{{ - 7}}{9}.\dfrac{3}{{11}} + \dfrac{{ - 7}}{{11}}.\dfrac{8}{9} + 5\dfrac{7}{9}\\ = \dfrac{{ - 7}}{9}.\dfrac{3}{{11}} + \dfrac{{ - 7}}{9}.\dfrac{8}{{11}} + 5\dfrac{7}{9}\\ = \dfrac{{ - 7}}{9}.\left( {\dfrac{3}{{11}} + \dfrac{8}{{11}}} \right) + 5 + \dfrac{7}{9}\\ = \dfrac{{ - 7}}{9} + \dfrac{7}{9} + 5\\ = 0 + 5 = 5\end{array}\)
Bài 2
Phương pháp:
Chuyển vế và đổi dấu để tìm x.
Cách giải:
a)
\(\begin{array}{l}x - \dfrac{1}{2} = \dfrac{{ - 2}}{3}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 2}}{3}\, + \dfrac{1}{2}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{6}\end{array}\)
b)
\(\begin{array}{l}\dfrac{2}{3}:x = 1,4 - \dfrac{{12}}{5}\\\dfrac{2}{3}:x = \dfrac{7}{5} - \dfrac{{12}}{5}\\\dfrac{2}{3}:x = - 1\\\,\,\,\,\,\,\,x = \dfrac{2}{3}:\left( { - 1} \right)\\\,\,\,\,\,\,\,x = \dfrac{{ - 2}}{3}\end{array}\)
c)
\(\begin{array}{l}{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2} + \dfrac{5}{9} = {2022^0}\\{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2} + \dfrac{5}{9} = 1\\{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2}\,\,\,\,\,\,\,\,\,\,\, = 1 - \dfrac{5}{9}\\{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2}\,\,\,\,\,\,\,\,\,\,\, = \dfrac{4}{9}\\{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2}\,\,\,\,\,\,\,\,\,\,\, = {\left( {\dfrac{2}{3}} \right)^2}\end{array}\)
TH1:
\(\begin{array}{l}\dfrac{1}{3} - \dfrac{2}{3}x = \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\dfrac{2}{3}x = \dfrac{1}{3} - \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\dfrac{2}{3}x = - \dfrac{1}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = - \dfrac{1}{3}\,:\dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = - \dfrac{1}{2}\end{array}\)
TH2:
\(\begin{array}{l}\dfrac{1}{3} - \dfrac{2}{3}x = \dfrac{{ - 2}}{3}\\\,\,\,\,\,\,\,\,\,\dfrac{2}{3}x = \dfrac{1}{3} - \dfrac{{ - 2}}{3}\\\,\,\,\,\,\,\,\,\,\dfrac{2}{3}x = 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = 1\,:\dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{3}{2}\end{array}\)
Bài 3
Phương pháp:
a) Lần lượt tính số học sinh giỏi, số học sinh khá và số học sinh trung bình.
b) Tỉ số phần trăm học sinh trung bình = Số học sinh trung bình : Số học sinh cả lớp × 100 (%)
Cách giải:
a) Số học sinh giỏi của lớp 6A là: \(48.\dfrac{{25}}{{100}} = 12\) (học sinh)
Số học sinh khá của lớp 6A là: \(12.1\dfrac{1}{3} = 12.\dfrac{4}{3} = 16\) (học sinh)
Số học sinh trung bình của lớp 6A là: \(48 - 12 - 16 = 20\) (học sinh)
b) Tỉ số phần trăm giữa số học sinh trung bình với số học sinh cả lớp là: \(\dfrac{{20}}{{48}}.100\% \approx 41,67\% \)
Bài 4
Phương pháp:
Sử dụng tính chất điểm nằm giữa, trung điểm của đoạn thẳng.
Cách giải:
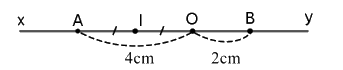
a) Hai tia đối nhau gốc A là: Ax và Ay
Hai tia trùng nhau gốc B là: BO và Bx
b) Vì O nằm giữa A và B nên ta có: \(AB = OA + AB = 4 + 2 = 6\left( {cm} \right)\)
c) Vì I là trung điểm của OA nên \(OI = \dfrac{1}{2}OA = \dfrac{1}{2}.4 = 2\left( {cm} \right)\)
Điểm O nằm giữa I và B, \(OI = OB = 2cm\) nên O là trung điểm của đoạn thẳng IB.
Bài 5
Phương pháp:
Biến đổi \(B = \dfrac{{10n - 3}}{{2\left( {2n - 5} \right)}} = \dfrac{5}{2} + \dfrac{{11}}{{2n - 5}}\).
B đạt giá trị lớn nhất khi và chỉ khi \(2n - 5 > 0\) và đạt giá trị nhỏ nhất
Từ đó suy ra n và giá trị lớn nhất của B.
Cách giải:
Ta có: \(B = \dfrac{{10n - 3}}{{2\left( {2n - 5} \right)}} = \dfrac{{10n - 25 + 22}}{{2\left( {2n - 5} \right)}} = \dfrac{{5\left( {2n - 5} \right) + 22}}{{2\left( {2n - 5} \right)}} = \dfrac{5}{2} + \dfrac{{11}}{{2n - 5}}\)
B đạt giá trị lớn nhất khi và chỉ khi \(\dfrac{{11}}{{2n - 5}}\) đạt giá trị lớn nhất.
\(\dfrac{{11}}{{2n - 5}}\) đạt giá trị lớn nhất khi và chỉ khi \(2n - 5 > 0\) và đạt giá trị nhỏ nhất
Suy ra: \(2n - 5 = 1\).
\(\begin{array}{l}2n = 6\\\,\,n = 3\end{array}\)
Khi đó: \(B = \dfrac{5}{2} + 11 = \dfrac{{27}}{2}\)
Vậy \(n = 3\) thì B đạt giá trị lớn nhất là \(\dfrac{{27}}{2}\).
Phần I: Trắc nghiệm
1. A | 2. A | 3. A | 4. D |
Câu 1
Phương pháp:
So sánh và sắp xếp theo thứ tự từ bé đến lớn.
Cách giải:
Các số xếp theo thứ tự từ bé đến lớn là: - 2,604; - 2,406; - 2,064; - 2,046
Chọn A.
Câu 2
Phương pháp:
Xác suất thực nghiệm xuất hiện màu vàng = Số lần xuất hiện màu vàng : Số lần thử
Cách giải:
Xác suất thực nghiệm xuất hiện màu vàng là: \(\dfrac{5}{{15}} = \dfrac{1}{3}\)
Chọn A.
Câu 3
Phương pháp:
Lấy giá trị chia cho phân số tương ứng.
Cách giải:
\(\begin{array}{l}\dfrac{2}{5}.x = 20\\\,\,\,\,\,x = 20:\dfrac{2}{5}\\\,\,\,\,\,x = 50\end{array}\)
Chọn A.
Câu 4
Phương pháp:
Kim phút và kim giờ của đồng hồ tạo thành góc bẹt tại thời điểm 6 giờ.
Cách giải:
Kim phút và kim giờ của đồng hồ tạo thành góc bẹt tại thời điểm 6 giờ.
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp
a) Thực hiện phép cộng hai phân số.
b) Nhóm thích hợp.
c) Sử dụng tính chất phân phối của phép nhân với phép cộng.
Cách giải:
a) \(\dfrac{1}{6} + \dfrac{{ - 5}}{3} = \dfrac{1}{6} + \dfrac{{ - 10}}{6} = \dfrac{{ - 9}}{6} = \dfrac{{ - 3}}{2}\)
b)
\(\begin{array}{l}\left( {2022,19 + 152,3} \right) - \left( {2022,19 - 7,7} \right)\\ = 2022,19 + 152,3 - 2022,19 + 7,7\\ = \left( {2022,19 - 2022,19} \right) + \left( {152,3 + 7,7} \right)\\ = 0 + 160 = 160\end{array}\)
c)
\(\begin{array}{l}\dfrac{{ - 7}}{9}.\dfrac{3}{{11}} + \dfrac{{ - 7}}{{11}}:\dfrac{9}{8} + 5\dfrac{7}{9}\\ = \dfrac{{ - 7}}{9}.\dfrac{3}{{11}} + \dfrac{{ - 7}}{{11}}.\dfrac{8}{9} + 5\dfrac{7}{9}\\ = \dfrac{{ - 7}}{9}.\dfrac{3}{{11}} + \dfrac{{ - 7}}{9}.\dfrac{8}{{11}} + 5\dfrac{7}{9}\\ = \dfrac{{ - 7}}{9}.\left( {\dfrac{3}{{11}} + \dfrac{8}{{11}}} \right) + 5 + \dfrac{7}{9}\\ = \dfrac{{ - 7}}{9} + \dfrac{7}{9} + 5\\ = 0 + 5 = 5\end{array}\)
Bài 2
Phương pháp:
Chuyển vế và đổi dấu để tìm x.
Cách giải:
a)
\(\begin{array}{l}x - \dfrac{1}{2} = \dfrac{{ - 2}}{3}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 2}}{3}\, + \dfrac{1}{2}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{6}\end{array}\)
b)
\(\begin{array}{l}\dfrac{2}{3}:x = 1,4 - \dfrac{{12}}{5}\\\dfrac{2}{3}:x = \dfrac{7}{5} - \dfrac{{12}}{5}\\\dfrac{2}{3}:x = - 1\\\,\,\,\,\,\,\,x = \dfrac{2}{3}:\left( { - 1} \right)\\\,\,\,\,\,\,\,x = \dfrac{{ - 2}}{3}\end{array}\)
c)
\(\begin{array}{l}{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2} + \dfrac{5}{9} = {2022^0}\\{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2} + \dfrac{5}{9} = 1\\{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2}\,\,\,\,\,\,\,\,\,\,\, = 1 - \dfrac{5}{9}\\{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2}\,\,\,\,\,\,\,\,\,\,\, = \dfrac{4}{9}\\{\left( {\dfrac{1}{3} - \dfrac{2}{3}x} \right)^2}\,\,\,\,\,\,\,\,\,\,\, = {\left( {\dfrac{2}{3}} \right)^2}\end{array}\)
TH1:
\(\begin{array}{l}\dfrac{1}{3} - \dfrac{2}{3}x = \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\dfrac{2}{3}x = \dfrac{1}{3} - \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\dfrac{2}{3}x = - \dfrac{1}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = - \dfrac{1}{3}\,:\dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = - \dfrac{1}{2}\end{array}\)
TH2:
\(\begin{array}{l}\dfrac{1}{3} - \dfrac{2}{3}x = \dfrac{{ - 2}}{3}\\\,\,\,\,\,\,\,\,\,\dfrac{2}{3}x = \dfrac{1}{3} - \dfrac{{ - 2}}{3}\\\,\,\,\,\,\,\,\,\,\dfrac{2}{3}x = 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = 1\,:\dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{3}{2}\end{array}\)
Bài 3
Phương pháp:
a) Lần lượt tính số học sinh giỏi, số học sinh khá và số học sinh trung bình.
b) Tỉ số phần trăm học sinh trung bình = Số học sinh trung bình : Số học sinh cả lớp × 100 (%)
Cách giải:
a) Số học sinh giỏi của lớp 6A là: \(48.\dfrac{{25}}{{100}} = 12\) (học sinh)
Số học sinh khá của lớp 6A là: \(12.1\dfrac{1}{3} = 12.\dfrac{4}{3} = 16\) (học sinh)
Số học sinh trung bình của lớp 6A là: \(48 - 12 - 16 = 20\) (học sinh)
b) Tỉ số phần trăm giữa số học sinh trung bình với số học sinh cả lớp là: \(\dfrac{{20}}{{48}}.100\% \approx 41,67\% \)
Bài 4
Phương pháp:
Sử dụng tính chất điểm nằm giữa, trung điểm của đoạn thẳng.
Cách giải:
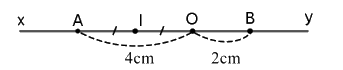
a) Hai tia đối nhau gốc A là: Ax và Ay
Hai tia trùng nhau gốc B là: BO và Bx
b) Vì O nằm giữa A và B nên ta có: \(AB = OA + AB = 4 + 2 = 6\left( {cm} \right)\)
c) Vì I là trung điểm của OA nên \(OI = \dfrac{1}{2}OA = \dfrac{1}{2}.4 = 2\left( {cm} \right)\)
Điểm O nằm giữa I và B, \(OI = OB = 2cm\) nên O là trung điểm của đoạn thẳng IB.
Bài 5
Phương pháp:
Biến đổi \(B = \dfrac{{10n - 3}}{{2\left( {2n - 5} \right)}} = \dfrac{5}{2} + \dfrac{{11}}{{2n - 5}}\).
B đạt giá trị lớn nhất khi và chỉ khi \(2n - 5 > 0\) và đạt giá trị nhỏ nhất
Từ đó suy ra n và giá trị lớn nhất của B.
Cách giải:
Ta có: \(B = \dfrac{{10n - 3}}{{2\left( {2n - 5} \right)}} = \dfrac{{10n - 25 + 22}}{{2\left( {2n - 5} \right)}} = \dfrac{{5\left( {2n - 5} \right) + 22}}{{2\left( {2n - 5} \right)}} = \dfrac{5}{2} + \dfrac{{11}}{{2n - 5}}\)
B đạt giá trị lớn nhất khi và chỉ khi \(\dfrac{{11}}{{2n - 5}}\) đạt giá trị lớn nhất.
\(\dfrac{{11}}{{2n - 5}}\) đạt giá trị lớn nhất khi và chỉ khi \(2n - 5 > 0\) và đạt giá trị nhỏ nhất
Suy ra: \(2n - 5 = 1\).
\(\begin{array}{l}2n = 6\\\,\,n = 3\end{array}\)
Khi đó: \(B = \dfrac{5}{2} + 11 = \dfrac{{27}}{2}\)
Vậy \(n = 3\) thì B đạt giá trị lớn nhất là \(\dfrac{{27}}{2}\).
Kỳ thi học kì 2 Toán 6 là một bước quan trọng để đánh giá mức độ nắm vững kiến thức của học sinh sau một học kỳ học tập. Đề thi học kì 2 Toán 6 - Đề số 6 tại giaitoan.edu.vn được thiết kế để giúp học sinh ôn luyện và tự tin hơn trong kỳ thi sắp tới. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết từng bài để học sinh có thể hiểu rõ hơn về kiến thức đã học.
Đề thi học kì 2 Toán 6 thường bao gồm các dạng bài tập sau:
Dưới đây là một số dạng bài tập thường gặp trong đề thi học kì 2 Toán 6:
Để giúp học sinh hiểu rõ hơn về cách giải các bài tập trong đề thi học kì 2 Toán 6, chúng ta sẽ cùng nhau giải chi tiết một số bài tập sau:
Cho biểu thức A = 2x + 3y. Tính giá trị của A khi x = 2 và y = -1.
Giải:
Thay x = 2 và y = -1 vào biểu thức A, ta có:
A = 2 * 2 + 3 * (-1) = 4 - 3 = 1
Vậy, giá trị của biểu thức A là 1.
Giải phương trình 3x - 5 = 7.
Giải:
3x - 5 = 7
3x = 7 + 5
3x = 12
x = 12 / 3
x = 4
Vậy, nghiệm của phương trình là x = 4.
Ngoài đề thi học kì 2 Toán 6 - Đề số 6 tại giaitoan.edu.vn, học sinh có thể tham khảo thêm các tài nguyên học tập sau:
Đề thi học kì 2 Toán 6 - Đề số 6 là một công cụ hữu ích để giúp học sinh ôn luyện và tự tin hơn trong kỳ thi sắp tới. Hy vọng rằng bài viết này đã cung cấp cho học sinh những thông tin hữu ích và giúp các em đạt kết quả tốt nhất trong kỳ thi.