Chào mừng các em học sinh lớp 6 đến với đề thi giữa kì 1 môn Toán - Đề số 14 của giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì.
Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp các em làm quen với nhiều dạng câu hỏi thường gặp trong các bài kiểm tra.
Phần trắc nghiệm Câu 1. Tập hợp các số tự nhiên là:
Phần trắc nghiệm
Câu 1. Tập hợp các số tự nhiên là:
A. \(\mathbb{N} = \left\{ {1;2;3; \ldots } \right\}\)
B. \(\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}\)
C. \(\mathbb{N} = \left\{ 0 \right\}\)
D. \(\mathbb{N} = \left\{ {0;1;2;3} \right\}\)
Câu 2. Số La Mã \(XXVII\) tương ứng giá trị bằng:
A. 27
B. 28
C. 29
D. 23
Câu 3. Chữ số 6 trong số 46 308 042 có giá trị bằng:
A. 6 000
B. 60 000
C. 600 000
D. 6 000 000
Câu 4. Đối với biểu thức không có ngoặc và chỉ có các phép tính: cộng, trừ, nhân, chia, lũy thừa, thì thứ tự thực hiện phép tính đúng là
A. Nhân và chia \( \to \) Lũy thừa \( \to \) Cộng và trừ.
B. Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ.
C. Cộng và trừ \( \to \) Nhân và chia \( \to \) Lũy thừa.
D. Lũy thừa \( \to \) Cộng và trừ \( \to \) Nhân và chia.
Câu 5. Nếu \(a = b.q\) (b khác 0). Khẳng định nào là SAI:
A. là ước của b
B. a chia hết cho b
C. a là bội của b
D. b là ước của a
Câu 6. Trong các số \(2;6;11;17;21;27\), hợp số là:
A. \(2;6;21\)
B. \(2;6;21;27\)
C. \(2;6;21\)
D. \(6;21;27\)
Câu 7. Trong các phép chia sau, phép chia là phép chia có dư là:
A. 21:7
B. \(12:4\)
C. \(16:5\)
D. \(24:6\)
Câu 8. Có bao nhiêu số nguyên tố nhỏ hơn 10?
A. 4
B. 5
C. 7
D. 3
Câu 9. Cụm từ thích hợp điền vào chỗ trống: "Trong hình thoi hai đường chéo cắt nhau..." là:
A. và vuông góc với nhau.
B. và bằng nhau.
C. tại trung điểm mỗi đường.
D. tại trung điểm mỗi đường và vuông góc.
Câu 10. Yếu tố nào sau đây không phải của hình chữ nhật:
A. Hai đường chéo bằng nhau
B. Hai cạnh đối bằng nhau
C. Bốn góc vuông
D. Bốn cạnh bằng nhau
Câu 11. Trong các hình sau, hình tam giác đều là:
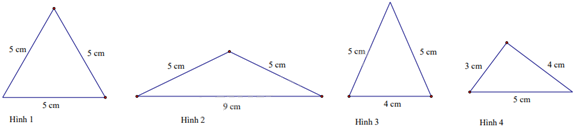
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Câu 12. Các đường chéo chính của lục giác đều trong hình sau là:
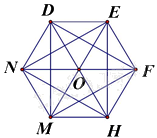
A. DH, EM, NF
B. EH, HN, NE
C. DM, EH, DH
D. DF, FM, MD
Phần tự luận
Câu 13.
a) Viết tập hợp các số tự nhiên lớn hơn 5 và nhỏ hơn 12 bằng cách liệt kê các phần tử.
b) Điền kí hiệu \(\left( { \in , \notin } \right)\) vào chỗ ... sau: 5 … A; 7 … A.
c) Trong tập hợp A. Viết các số là bội của 2; Viết các số là ước 18.
Câu 14.
a) Tính nhanh: \(38.63 + 37.38\)
b) Tìm \(x\) biết: \({3^6}:x = {3^2}{.3^3}\)
Câu 15.
Đầu năm học một số bạn trong lớp 6 nhận được quà của các mạnh thường quân là 109 quyển vở và 83 cái bút. Biết rằng khi chia 109 quyển vở cho các em thì dư 13 quyển. Còn khi chia 83 cái bút cho các em thì dư 11. Tính xem lớp 6 có bao nhiêu bạn nhận được quà (biết rằng số vở và số bút mỗi bạn nhận được là như nhau).
Câu 16.
Vẽ hình chữ nhật có cạnh AB = 3 cm, cạnh BC = 5 cm.
a) Viết tên các cạnh đối của hình chữ nhật ABCD.
b) Tính diện tích hình chữ nhật ABCD.
-------- Hết --------
Phần trắc nghiệm
1.B | 2.A | 3.D | 4.B | 5.A | 6.D |
7.C | 8.A | 9.D | 10.D | 11.A | 12.A |
Câu 1. Tập hợp các số tự nhiên là:
A. \(\mathbb{N} = \left\{ {1;2;3; \ldots } \right\}\)
B. \(\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}\)
C. \(\mathbb{N} = \left\{ 0 \right\}\)
D. \(\mathbb{N} = \left\{ {0;1;2;3} \right\}\)
Phương pháp:
Nhận biết tập hợp số tự nhiên.
Lời giải:
Tập hợp các số tự nhiên là: \(\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}\)
Đáp án B.
Câu 2. Số La Mã \(XXVII\) tương ứng giá trị bằng:
A. 27
B. 28
C. 29
D. 23
Phương pháp:
Viết số La Mã dưới dạng số tự nhiên.
Lời giải:
Số La Mã tương ứng giá trị bằng 27.
Đáp án A.
Câu 3. Chữ số 6 trong số 46 308 042 có giá trị bằng:
A. 6 000
B. 60 000
C. 600 000
D. 6 000 000
Phương pháp:
Xác định vị trí của chữ số 6, từ đó suy ra giá trị.
Lời giải:
Chữ số 6 trong số 46 308 042 có giá trị bằng 6 000 000.
Đáp án D.
Câu 4. Đối với biểu thức không có ngoặc và chỉ có các phép tính: cộng, trừ, nhân, chia, lũy thừa, thì thứ tự thực hiện phép tính đúng là
A. Nhân và chia \( \to \) Lũy thừa \( \to \) Cộng và trừ.
B. Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ.
C. Cộng và trừ \( \to \) Nhân và chia \( \to \) Lũy thừa.
D. Lũy thừa \( \to \) Cộng và trừ \( \to \) Nhân và chia.
Phương pháp:
Sử dụng quy tắc về thứ tự thực hiện các phép tính.
Lời giải:
Đối với biểu thức không có ngoặc và chỉ có các phép tính: cộng, trừ, nhân, chia, lũy thừa, thì thứ tự thực hiện phép tính đúng là: Lũy thừa → Nhân và chia → Cộng và trừ.
Đáp án B.
Câu 5. Nếu \(a = b.q\) (b khác 0). Khẳng định nào là SAI:
A. là ước của b
B. a chia hết cho b
C. a là bội của b
D. b là ước của a
Phương pháp:
Sử dụng khái niệm bội và ước.
Lời giải:
Nếu ( khác 0) thì là bội của ; \(b\) là ước của \(a\)và \(a\) chia hết cho \(b.\)
Đáp án A.
Câu 6. Trong các số \(2;6;11;17;21;27\), hợp số là:
A. \(2;6;21\)
B. \(2;6;21;27\)
C. \(2;6;21\)
D. \(6;21;27\)
Phương pháp:
Dựa vào khái niệm hợp số.
Lời giải:
Trong các số , hợp số là: \(6;21;27\)
Đáp án D.
Câu 7. Trong các phép chia sau, phép chia là phép chia có dư là:
A. 21:7
B. \(12:4\)
C. \(16:5\)
D. \(24:6\)
Phương pháp:
Kiểm tra các phép chia là chia hết hay chia dư.
Lời giải:
Vì 16 không chia hết cho 5 nên là phép chia có dư.
Đáp án C.
Câu 8. Có bao nhiêu số nguyên tố nhỏ hơn 10?
A. 4
B. 5
C. 7
D. 3
Phương pháp:
Liệt kê và đếm các số nguyên tố nhỏ hơn 10.
Lời giải:
Có 4 số nguyên tố nhỏ hơn 10 là: 2; 3; 5; 7.
Đáp án A.
Câu 9. Cụm từ thích hợp điền vào chỗ trống: "Trong hình thoi hai đường chéo cắt nhau..." là:
A. và vuông góc với nhau.
B. và bằng nhau.
C. tại trung điểm mỗi đường.
D. tại trung điểm mỗi đường và vuông góc.
Phương pháp:
Sử dụng tính chất của hình thoi.
Lời giải:
Trong hình thoi hai đường chéo cắt nhau tại trung điểm mỗi đường.
Đáp án D.
Câu 10. Yếu tố nào sau đây không phải của hình chữ nhật:
A. Hai đường chéo bằng nhau
B. Hai cạnh đối bằng nhau
C. Bốn góc vuông
D. Bốn cạnh bằng nhau
Phương pháp:
Sử dụng tính chất của hình chữ nhật.
Lời giải:
Hình chữ nhật không có bốn cạnh bằng nhau.
Đáp án D.
Câu 11. Trong các hình sau, hình tam giác đều là:
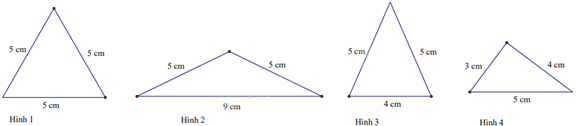
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Phương pháp:
Nhận biết hình tam giác đều.
Lời giải:
Hình 1 là hình tam giác đều.
Đáp án A.
Câu 12. Các đường chéo chính của lục giác đều trong hình sau là:
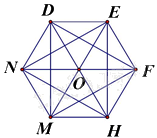
A. DH, EM, NF
B. EH, HN, NE
C. DM, EH, DH
D. DF, FM, MD
Phương pháp:
Các đường chéo chính của hình lục giác đều là các đường chéo đi qua tâm.
Lời giải:
Các đường chéo chính của hình của lục giác đều là: DH, EM, NF.
Đáp án A.
Phần tự luận.
Câu 13.
a) Viết tập hợp các số tự nhiên lớn hơn 5 và nhỏ hơn 12 bằng cách liệt kê các phần tử.
b) Điền kí hiệu \(\left( { \in , \notin } \right)\) vào chỗ ... sau: 5 … A; 7 … A.
c) Trong tập hợp A. Viết các số là bội của 2; Viết các số là ước 18.
Phương pháp:
- Viết tập hợp, xác định các phần tử thuộc hay không thuộc tập hợp.
- Sử dụng khái niệm ước và bội.
Lời giải:
a. Tập hợp \({\rm{A}}\) các số tự nhiên lớn hơn 5 và nhỏ hơn 12: \({\rm{A}} = \{ 6;7;8;9;10;11\} \)
b. \(5 \notin {\rm{A}}\) \(7 \in {\rm{A}}\)
c. Trong tập hợp A:
Các số là bội của 2 là: 6; 8; 10.
Các số là ước 18 là: 6; 9.
Câu 14.
a) Tính nhanh: \(38.63 + 37.38\)
b) Tìm \(x\) biết: \({3^6}:x = {3^2}{.3^3}\)
Phương pháp:
Áp dụng các quy tắc thực hiện phép tính.
Lời giải:
\(\begin{array}{l}{\rm{a}})\,\,38.63 + 37.38\\\,\, = 38.(63 + 37)\\\,\, = 38.100\\\,\, = 3800\end{array}\)
\(\begin{array}{l}{\rm{b}})\,\,{3^6}:x = {3^2} \cdot {3^3}\\\,\,\,\,\,\,{3^6}:x = {3^5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = {3^6}:{3^5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 3\end{array}\)
Câu 15.
Đầu năm học một số bạn trong lớp 6 nhận được quà của các mạnh thường quân là 109 quyển vở và 83 cái bút. Biết rằng khi chia 109 quyển vở cho các em thì dư 13 quyển. Còn khi chia 83 cái bút cho các em thì dư 11. Tính xem lớp 6 có bao nhiêu bạn nhận được quà (biết rằng số vở và số bút mỗi bạn nhận được là như nhau).
Phương pháp:
Gọi số học sinh của lớp 6 nhận được quà là \(a\,\left( {a \in \mathbb{N}} \right).\)
Từ các điều kiện đề bài cho suy ra: \(a \in {\rm{UC}}(96,72)\). Từ đó tìm được \(a.\)
Lời giải:
Gọi số học sinh của lớp 6 nhận được quà là \(a\,\left( {a \in \mathbb{N}} \right).\)
Vì 109 chia cho \(a\) dư 13 nên \(\left( {109 - 13} \right) \vdots a\) hay \(96 \vdots a\) và \(a > 13\) (1)
83 chia cho \(a\) dư 11 nên \((83 - 11):a\) hay \(72 \vdots a\)và \(a > 11\) (2)
Từ (1) và (2) suy ra \(a \in {\rm{UC}}(96,72)\) và \(a > 13\).
\({\rm{UCLN}}(96,72) = 24\)
Ước chung của 96 và 72 mà lớn hơn 13 là 24.
Suy ra \(a = 24\).
Vậy lớp 6 có 24 bạn nhận được quà.
Câu 16.
Vẽ hình chữ nhật có cạnh AB = 3 cm, cạnh BC = 5 cm.
a) Viết tên các cạnh đối của hình chữ nhật ABCD.
b) Tính diện tích hình chữ nhật ABCD.
Phương pháp:
- Vẽ hình chữ nhật, nêu các cặp cạnh đối.
- Áp dụng công thức tính diện tích hình chữ nhật.
Lời giải:
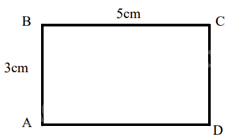
a) Các cạnh đối của hình chữ nhật AB và CD; BC và AD.
b) Diện tích hình chữ nhật ABCD là: \(3.5 = 15\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\)
Tải về
Phần trắc nghiệm
Câu 1. Tập hợp các số tự nhiên là:
A. \(\mathbb{N} = \left\{ {1;2;3; \ldots } \right\}\)
B. \(\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}\)
C. \(\mathbb{N} = \left\{ 0 \right\}\)
D. \(\mathbb{N} = \left\{ {0;1;2;3} \right\}\)
Câu 2. Số La Mã \(XXVII\) tương ứng giá trị bằng:
A. 27
B. 28
C. 29
D. 23
Câu 3. Chữ số 6 trong số 46 308 042 có giá trị bằng:
A. 6 000
B. 60 000
C. 600 000
D. 6 000 000
Câu 4. Đối với biểu thức không có ngoặc và chỉ có các phép tính: cộng, trừ, nhân, chia, lũy thừa, thì thứ tự thực hiện phép tính đúng là
A. Nhân và chia \( \to \) Lũy thừa \( \to \) Cộng và trừ.
B. Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ.
C. Cộng và trừ \( \to \) Nhân và chia \( \to \) Lũy thừa.
D. Lũy thừa \( \to \) Cộng và trừ \( \to \) Nhân và chia.
Câu 5. Nếu \(a = b.q\) (b khác 0). Khẳng định nào là SAI:
A. là ước của b
B. a chia hết cho b
C. a là bội của b
D. b là ước của a
Câu 6. Trong các số \(2;6;11;17;21;27\), hợp số là:
A. \(2;6;21\)
B. \(2;6;21;27\)
C. \(2;6;21\)
D. \(6;21;27\)
Câu 7. Trong các phép chia sau, phép chia là phép chia có dư là:
A. 21:7
B. \(12:4\)
C. \(16:5\)
D. \(24:6\)
Câu 8. Có bao nhiêu số nguyên tố nhỏ hơn 10?
A. 4
B. 5
C. 7
D. 3
Câu 9. Cụm từ thích hợp điền vào chỗ trống: "Trong hình thoi hai đường chéo cắt nhau..." là:
A. và vuông góc với nhau.
B. và bằng nhau.
C. tại trung điểm mỗi đường.
D. tại trung điểm mỗi đường và vuông góc.
Câu 10. Yếu tố nào sau đây không phải của hình chữ nhật:
A. Hai đường chéo bằng nhau
B. Hai cạnh đối bằng nhau
C. Bốn góc vuông
D. Bốn cạnh bằng nhau
Câu 11. Trong các hình sau, hình tam giác đều là:
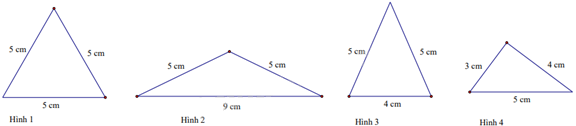
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Câu 12. Các đường chéo chính của lục giác đều trong hình sau là:
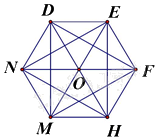
A. DH, EM, NF
B. EH, HN, NE
C. DM, EH, DH
D. DF, FM, MD
Phần tự luận
Câu 13.
a) Viết tập hợp các số tự nhiên lớn hơn 5 và nhỏ hơn 12 bằng cách liệt kê các phần tử.
b) Điền kí hiệu \(\left( { \in , \notin } \right)\) vào chỗ ... sau: 5 … A; 7 … A.
c) Trong tập hợp A. Viết các số là bội của 2; Viết các số là ước 18.
Câu 14.
a) Tính nhanh: \(38.63 + 37.38\)
b) Tìm \(x\) biết: \({3^6}:x = {3^2}{.3^3}\)
Câu 15.
Đầu năm học một số bạn trong lớp 6 nhận được quà của các mạnh thường quân là 109 quyển vở và 83 cái bút. Biết rằng khi chia 109 quyển vở cho các em thì dư 13 quyển. Còn khi chia 83 cái bút cho các em thì dư 11. Tính xem lớp 6 có bao nhiêu bạn nhận được quà (biết rằng số vở và số bút mỗi bạn nhận được là như nhau).
Câu 16.
Vẽ hình chữ nhật có cạnh AB = 3 cm, cạnh BC = 5 cm.
a) Viết tên các cạnh đối của hình chữ nhật ABCD.
b) Tính diện tích hình chữ nhật ABCD.
-------- Hết --------
Phần trắc nghiệm
1.B | 2.A | 3.D | 4.B | 5.A | 6.D |
7.C | 8.A | 9.D | 10.D | 11.A | 12.A |
Câu 1. Tập hợp các số tự nhiên là:
A. \(\mathbb{N} = \left\{ {1;2;3; \ldots } \right\}\)
B. \(\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}\)
C. \(\mathbb{N} = \left\{ 0 \right\}\)
D. \(\mathbb{N} = \left\{ {0;1;2;3} \right\}\)
Phương pháp:
Nhận biết tập hợp số tự nhiên.
Lời giải:
Tập hợp các số tự nhiên là: \(\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}\)
Đáp án B.
Câu 2. Số La Mã \(XXVII\) tương ứng giá trị bằng:
A. 27
B. 28
C. 29
D. 23
Phương pháp:
Viết số La Mã dưới dạng số tự nhiên.
Lời giải:
Số La Mã tương ứng giá trị bằng 27.
Đáp án A.
Câu 3. Chữ số 6 trong số 46 308 042 có giá trị bằng:
A. 6 000
B. 60 000
C. 600 000
D. 6 000 000
Phương pháp:
Xác định vị trí của chữ số 6, từ đó suy ra giá trị.
Lời giải:
Chữ số 6 trong số 46 308 042 có giá trị bằng 6 000 000.
Đáp án D.
Câu 4. Đối với biểu thức không có ngoặc và chỉ có các phép tính: cộng, trừ, nhân, chia, lũy thừa, thì thứ tự thực hiện phép tính đúng là
A. Nhân và chia \( \to \) Lũy thừa \( \to \) Cộng và trừ.
B. Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ.
C. Cộng và trừ \( \to \) Nhân và chia \( \to \) Lũy thừa.
D. Lũy thừa \( \to \) Cộng và trừ \( \to \) Nhân và chia.
Phương pháp:
Sử dụng quy tắc về thứ tự thực hiện các phép tính.
Lời giải:
Đối với biểu thức không có ngoặc và chỉ có các phép tính: cộng, trừ, nhân, chia, lũy thừa, thì thứ tự thực hiện phép tính đúng là: Lũy thừa → Nhân và chia → Cộng và trừ.
Đáp án B.
Câu 5. Nếu \(a = b.q\) (b khác 0). Khẳng định nào là SAI:
A. là ước của b
B. a chia hết cho b
C. a là bội của b
D. b là ước của a
Phương pháp:
Sử dụng khái niệm bội và ước.
Lời giải:
Nếu ( khác 0) thì là bội của ; \(b\) là ước của \(a\)và \(a\) chia hết cho \(b.\)
Đáp án A.
Câu 6. Trong các số \(2;6;11;17;21;27\), hợp số là:
A. \(2;6;21\)
B. \(2;6;21;27\)
C. \(2;6;21\)
D. \(6;21;27\)
Phương pháp:
Dựa vào khái niệm hợp số.
Lời giải:
Trong các số , hợp số là: \(6;21;27\)
Đáp án D.
Câu 7. Trong các phép chia sau, phép chia là phép chia có dư là:
A. 21:7
B. \(12:4\)
C. \(16:5\)
D. \(24:6\)
Phương pháp:
Kiểm tra các phép chia là chia hết hay chia dư.
Lời giải:
Vì 16 không chia hết cho 5 nên là phép chia có dư.
Đáp án C.
Câu 8. Có bao nhiêu số nguyên tố nhỏ hơn 10?
A. 4
B. 5
C. 7
D. 3
Phương pháp:
Liệt kê và đếm các số nguyên tố nhỏ hơn 10.
Lời giải:
Có 4 số nguyên tố nhỏ hơn 10 là: 2; 3; 5; 7.
Đáp án A.
Câu 9. Cụm từ thích hợp điền vào chỗ trống: "Trong hình thoi hai đường chéo cắt nhau..." là:
A. và vuông góc với nhau.
B. và bằng nhau.
C. tại trung điểm mỗi đường.
D. tại trung điểm mỗi đường và vuông góc.
Phương pháp:
Sử dụng tính chất của hình thoi.
Lời giải:
Trong hình thoi hai đường chéo cắt nhau tại trung điểm mỗi đường.
Đáp án D.
Câu 10. Yếu tố nào sau đây không phải của hình chữ nhật:
A. Hai đường chéo bằng nhau
B. Hai cạnh đối bằng nhau
C. Bốn góc vuông
D. Bốn cạnh bằng nhau
Phương pháp:
Sử dụng tính chất của hình chữ nhật.
Lời giải:
Hình chữ nhật không có bốn cạnh bằng nhau.
Đáp án D.
Câu 11. Trong các hình sau, hình tam giác đều là:
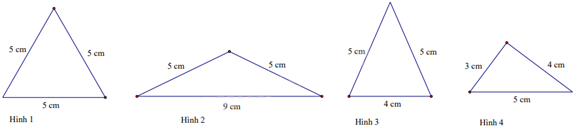
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Phương pháp:
Nhận biết hình tam giác đều.
Lời giải:
Hình 1 là hình tam giác đều.
Đáp án A.
Câu 12. Các đường chéo chính của lục giác đều trong hình sau là:
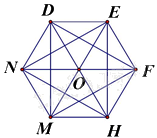
A. DH, EM, NF
B. EH, HN, NE
C. DM, EH, DH
D. DF, FM, MD
Phương pháp:
Các đường chéo chính của hình lục giác đều là các đường chéo đi qua tâm.
Lời giải:
Các đường chéo chính của hình của lục giác đều là: DH, EM, NF.
Đáp án A.
Phần tự luận.
Câu 13.
a) Viết tập hợp các số tự nhiên lớn hơn 5 và nhỏ hơn 12 bằng cách liệt kê các phần tử.
b) Điền kí hiệu \(\left( { \in , \notin } \right)\) vào chỗ ... sau: 5 … A; 7 … A.
c) Trong tập hợp A. Viết các số là bội của 2; Viết các số là ước 18.
Phương pháp:
- Viết tập hợp, xác định các phần tử thuộc hay không thuộc tập hợp.
- Sử dụng khái niệm ước và bội.
Lời giải:
a. Tập hợp \({\rm{A}}\) các số tự nhiên lớn hơn 5 và nhỏ hơn 12: \({\rm{A}} = \{ 6;7;8;9;10;11\} \)
b. \(5 \notin {\rm{A}}\) \(7 \in {\rm{A}}\)
c. Trong tập hợp A:
Các số là bội của 2 là: 6; 8; 10.
Các số là ước 18 là: 6; 9.
Câu 14.
a) Tính nhanh: \(38.63 + 37.38\)
b) Tìm \(x\) biết: \({3^6}:x = {3^2}{.3^3}\)
Phương pháp:
Áp dụng các quy tắc thực hiện phép tính.
Lời giải:
\(\begin{array}{l}{\rm{a}})\,\,38.63 + 37.38\\\,\, = 38.(63 + 37)\\\,\, = 38.100\\\,\, = 3800\end{array}\)
\(\begin{array}{l}{\rm{b}})\,\,{3^6}:x = {3^2} \cdot {3^3}\\\,\,\,\,\,\,{3^6}:x = {3^5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = {3^6}:{3^5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 3\end{array}\)
Câu 15.
Đầu năm học một số bạn trong lớp 6 nhận được quà của các mạnh thường quân là 109 quyển vở và 83 cái bút. Biết rằng khi chia 109 quyển vở cho các em thì dư 13 quyển. Còn khi chia 83 cái bút cho các em thì dư 11. Tính xem lớp 6 có bao nhiêu bạn nhận được quà (biết rằng số vở và số bút mỗi bạn nhận được là như nhau).
Phương pháp:
Gọi số học sinh của lớp 6 nhận được quà là \(a\,\left( {a \in \mathbb{N}} \right).\)
Từ các điều kiện đề bài cho suy ra: \(a \in {\rm{UC}}(96,72)\). Từ đó tìm được \(a.\)
Lời giải:
Gọi số học sinh của lớp 6 nhận được quà là \(a\,\left( {a \in \mathbb{N}} \right).\)
Vì 109 chia cho \(a\) dư 13 nên \(\left( {109 - 13} \right) \vdots a\) hay \(96 \vdots a\) và \(a > 13\) (1)
83 chia cho \(a\) dư 11 nên \((83 - 11):a\) hay \(72 \vdots a\)và \(a > 11\) (2)
Từ (1) và (2) suy ra \(a \in {\rm{UC}}(96,72)\) và \(a > 13\).
\({\rm{UCLN}}(96,72) = 24\)
Ước chung của 96 và 72 mà lớn hơn 13 là 24.
Suy ra \(a = 24\).
Vậy lớp 6 có 24 bạn nhận được quà.
Câu 16.
Vẽ hình chữ nhật có cạnh AB = 3 cm, cạnh BC = 5 cm.
a) Viết tên các cạnh đối của hình chữ nhật ABCD.
b) Tính diện tích hình chữ nhật ABCD.
Phương pháp:
- Vẽ hình chữ nhật, nêu các cặp cạnh đối.
- Áp dụng công thức tính diện tích hình chữ nhật.
Lời giải:
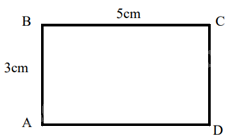
a) Các cạnh đối của hình chữ nhật AB và CD; BC và AD.
b) Diện tích hình chữ nhật ABCD là: \(3.5 = 15\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\)
Đề thi giữa kì 1 Toán 6 - Đề số 14 là một công cụ quan trọng giúp học sinh lớp 6 đánh giá năng lực và kiến thức đã học trong nửa học kỳ đầu tiên. Đề thi này thường bao gồm các chủ đề chính như số tự nhiên, phép tính với số tự nhiên, ước và bội, tập hợp, và các bài toán thực tế liên quan.
Thông thường, đề thi giữa kì 1 Toán 6 - Đề số 14 sẽ có cấu trúc gồm các phần sau:
Để giúp các em học sinh ôn tập hiệu quả, chúng ta sẽ đi sâu vào phân tích nội dung chi tiết của đề thi giữa kì 1 Toán 6 - Đề số 14. Dưới đây là một số dạng bài tập thường gặp:
Đây là phần kiến thức cơ bản nhất trong chương trình Toán 6. Đề thi thường yêu cầu học sinh:
Phần này kiểm tra khả năng của học sinh trong việc tìm ước và bội của một số. Đề thi có thể yêu cầu:
Kiến thức về tập hợp giúp học sinh hiểu rõ hơn về cách tổ chức và phân loại các đối tượng. Đề thi thường yêu cầu:
Các bài toán thực tế giúp học sinh áp dụng kiến thức đã học vào giải quyết các tình huống trong cuộc sống. Đề thi có thể yêu cầu:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 6, các em học sinh cần:
Ngoài việc giải đề thi, các em học sinh có thể tham khảo thêm các tài liệu ôn tập sau:
Đề thi giữa kì 1 Toán 6 - Đề số 14 là một cơ hội tốt để các em học sinh kiểm tra và củng cố kiến thức. Hy vọng rằng với những hướng dẫn chi tiết trên, các em sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em học tốt!