Đề thi giữa kì 1 Toán 6 - Đề số 11 là một công cụ ôn tập vô cùng hữu ích cho các em học sinh. Đề thi này được thiết kế bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp đề thi giữa kì 1 Toán 6 - Đề số 11 kèm theo đáp án chi tiết, giúp các em tự học và kiểm tra kiến thức một cách hiệu quả.
Phần trắc nghiệm Câu 1: Tập hợp ({rm{P}}) các số tự nhiên lớn hơn 8 có thể viết là
Phần trắc nghiệm
Câu 1: Tập hợp \({\rm{P}}\) các số tự nhiên lớn hơn 8 có thể viết là
A. \(P = \{ x \in N\mid x < 8\} \)
B. \(P = \{ x \in N\mid x > 8\} \)
C. \(P = \left\{ {x \in N\mid x \le 8} \right\}\)
D. \(P = \left\{ {x \in N\mid x \ge 8} \right\}\)
Câu 2: Chỉ ra cặp số tự nhiên liền trước và liền sau của số 101.
A. 100 và 102
B. 100 và 103
C. 99 và 100
D. 99 và 103
Câu 3: Số nào sau đây là số nguyên tố?
A. 2.
B. 21
C. 15.
D. 1
Câu 4: Cho tập hợp \({\rm{A}} = \left\{ {{\rm{a}};1;{\rm{b}};5} \right\}\). Chọn khẳng định đúng.
A. \(5 \in A\)
B. \(0 \in {\rm{A}}\)
C. \(1 \notin {\rm{A}}\)
D. \(a \notin A\)
Câu 5: Số nào sau đây là bội của 7?
A. 1
B. 3
C. 49
D. 16
Câu 6: Số nào sau đây là ước của 30?
A. 15.
B. 18.
C. 22.
D. 20
Câu 7: Kết quả phép tính \({6^3}.36\) là
A. \({6^3}\)
B. \({6^4}\)
C. \({6^5}\)
D. \({6^6}\)
Câu 8: U’CLN \(\left( {10;12} \right)\) là
A. 1
B. 2
C. 4
D. 12
Câu 9: Chu vi của hình tam giác đều có độ dài cạnh \(8{\rm{\;cm}}\)là
A. \(24{\rm{\;cm}}\)
B. \(24{\rm{\;c}}{{\rm{m}}^2}\)
C. \(512\,{\rm{cm}}\)
D. \(512{\rm{\;c}}{{\rm{m}}^2}\)
Câu 10: Cho hình bình hành \(ABCD\). Nhận xét đúng là
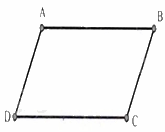
A. \(AB = AD\)
B. \(AD = BC\)
C. \({\rm{AB}} = {\rm{BC}}\)
D. \({\rm{BC}} = {\rm{CD}}\)
Phần tự luận
Bài 1: Thực hiện phép tính (bằng cách hợp lý nếu có thể):
a) \(525 + 120 + 475 + 380\)
b) \(123.35 + 66.123 - 123\)
c) \(170:\left\{ {54 - \left[ {120:4 - \left( {{4^2} - 3.2} \right)} \right]} \right\}\)
Bài 2: Tìm tất cả các ước chung của 28 và 56, từ đó tìm \({\rm{U}}CLN\left( {28;56} \right)\).
Bài 3: Hãy vẽ hình chữ nhật \({\rm{ABCD}}\) có độ dài cạnh \({\rm{AB}} = 4{\rm{\;cm}}\)và \({\rm{AD}} = 6{\rm{\;cm}}\). Tính chu vi và diện tích hình chữ nhật \(ABCD\).
Bài 4: Hội chữ thập đỏ ở một phường dự định tặng các suất quà cho các gia đình có hoàn cảnh khó khăn trong đợt dịch Covid 19. Dự định mỗi gói quà tặng bao gồm 1 bao gạo giá 220 000 đồng/bao; 2 kg lạc giá 50 000 đồng/kg; 5 gói gia vị giá 5000 đồng/gói, 2 chai dầu ăn giá 40 000 đồng/chai. Hỏi mỗi gói quà có tổng giá trị bao nhiêu tiền?
Bài 5: Tìm số tự nhiên \(n > 0\) sao cho \(n + 3\) chia hết cho \(n + 1\).
-------- Hết --------
Phần trắc nghiệm
1.B | 2.A | 3.A | 4.A | 5.C | 6.A | 7.C | 8.B | 9.A | 10.B |
Câu 1: Tập hợp \({\rm{P}}\) các số tự nhiên lớn hơn 8 có thể viết là
A. \(P = \{ x \in N\mid x < 8\} \)
B. \(P = \{ x \in N\mid x > 8\} \)
C. \(P = \left\{ {x \in N\mid x \le 8} \right\}\)
D. \(P = \left\{ {x \in N\mid x \ge 8} \right\}\)
Phương pháp:
Viết tập hợp.
Lời giải:
Tập hợp \({\rm{P}}\)các số tự nhiên lớn hơn 8 có thể viết là \(P = \{ x \in N\mid x > 8\} \).
Đáp án B.
Câu 2: Chỉ ra cặp số tự nhiên liền trước và liền sau của số 101.
A. 100 và 102
B. 100 và 103
C. 99 và 100
D. 99 và 103
Phương pháp:
Sử dụng định nghĩa số liền trước, liền sau của một số tự nhiên.
Lời giải:
Cặp số tự nhiên liền trước và liền sau của số 101 lần lượt là: 100 và 102.
Đáp án A.
Câu 3: Số nào sau đây là số nguyên tố?
A. 2.
B. 21
C. 15.
D. 1
Phương pháp:
Sử dụng khái niệm số nguyên tố.
Lời giải:
2 là số nguyên tố.
Đáp án A.
Câu 4: Cho tập hợp \({\rm{A}} = \left\{ {{\rm{a}};1;{\rm{b}};5} \right\}\). Chọn khẳng định đúng.
A. \(5 \in A\)
B. \(0 \in {\rm{A}}\)
C. \(1 \notin {\rm{A}}\)
D. \(a \notin A\)
Phương pháp:
Sử dụng kí hiệu thuộc hoặc không thuộc.
Lời giải:
\(5\) thuộc tập \(A\). Ta có: \(5 \in A\)
Đáp án A.
Câu 5: Số nào sau đây là bội của 7?
A. 1
B. 3
C. 49
D. 16
Phương pháp:
Sử dụng khái niệm bội và ước của một số nguyên:
Nếu \(a,b,x \in \mathbb{N}\) và \(a = b.x\) thì \(a \vdots b\) và a là một bội của b; b là một ước của a.
Lời giải:
49 chia hết cho 7 nên 49 là bội của 7.
Đáp án C.
Câu 6: Số nào sau đây là ước của 30?
A. 15.
B. 18.
C. 22.
D. 20
Phương pháp:
Sử dụng khái niệm bội và ước của một số nguyên:
Nếu \(a,b,x \in \mathbb{N}\) và \(a = b.x\) thì \(a \vdots b\) và a là một bội của b; b là một ước của a.
Lời giải:
30 chia hết cho 15 nên 15 là ước của 30.
Đáp án A.
Câu 7: Kết quả phép tính \({6^3}.36\) là
A. \({6^3}\)
B. \({6^4}\)
C. \({6^5}\)
D. \({6^6}\)
Phương pháp:
Viết 36 dưới dạng lũy thừa cơ số 6 rồi áp dụng công thức nhân hai lũy thừa.
\({a^m}.{a^n} = {a^{m + n}}\) (với \(a,m,n \in \mathbb{N}\))
Lời giải:
\({6^3}.36 = {6^3}{.6^2} = {6^5}\)
Đáp án C.
Câu 8: U’CLN \(\left( {10;12} \right)\) là
A. 1
B. 2
C. 4
D. 12
Phương pháp:
Vận dụng quy tắc tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Tích đó là ƯCLN phải tìm.
Lời giải:
Ta có: \(10 = 2.5;\,\,12 = {2^2}.3\)
Vậy U’CLN \(\left( {10;12} \right) = 2\)
Đáp án B.
Câu 9: Chu vi của hình tam giác đều có độ dài cạnh \(8{\rm{\;cm}}\)là
A. \(24{\rm{\;cm}}\)
B. \(24{\rm{\;c}}{{\rm{m}}^2}\)
C. \(512\,{\rm{cm}}\)
D. \(512{\rm{\;c}}{{\rm{m}}^2}\)
Phương pháp:
Chu vi tam giác đều cạnh \(a\) là: \(C = 3.a\)
Lời giải:
Chu vi của hình tam giác đều có độ dài cạnh \(8{\rm{\;cm}}\) là \(8 \times 3 = 24\left( {{\rm{cm}}} \right)\)
Đáp án A.
Câu 10: Cho hình bình hành \(ABCD\). Nhận xét đúng là
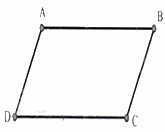
A. \(AB = AD\)
B. \(AD = BC\)
C. \({\rm{AB}} = {\rm{BC}}\)
D. \({\rm{BC}} = {\rm{CD}}\)
Phương pháp:
Nhận biết đặc điểm của hình bình hành.
Lời giải:
Hình hình hành ABCD có \(AD = BC.\)
Đáp án B.
Phần tự luận.
Bài 1: Thực hiện phép tính (bằng cách hợp lý nếu có thể):
a) \(525 + 120 + 475 + 380\)
b) \(123.35 + 66.123 - 123\)
c) \(170:\left\{ {54 - \left[ {120:4 - \left( {{4^2} - 3.2} \right)} \right]} \right\}\)
Phương pháp:
Áp dụng các quy tắc tính cộng, trừ, nhân, chia, lũy thừa.
Lời giải:
\(\begin{array}{l}a)\,\,525 + 120 + 475 + 380\\ = \left( {525 + 475} \right) + \left( {120 + 380} \right)\\ = 1000 + 500\\ = 1500\end{array}\)
\(\begin{array}{l}b)\,\,123.35 + 66.123 - 123\\ = 123.\left( {35 + 66 - 1} \right)\\ = 123.100\\ = 12300\end{array}\)
\(\begin{array}{l}c)\,\,170:\left\{ {54 - \left[ {120:4 - \left( {{4^2} - 3.2} \right)} \right]} \right\}\\ = 170:\left\{ {54 - \left[ {120:4 - \left( {16 - 6} \right)} \right]} \right\}\\ = 170:\left[ {54 - \left( {120:4 - 10} \right)} \right]\\ = 170:\left[ {54 - \left( {30 - 10} \right)} \right]\\ = 170:\left( {54 - 20} \right)\\ = 170:34\\ = 5\end{array}\)
Bài 2: Tìm tất cả các ước chung của 28 và 56, từ đó tìm \({\rm{U}}CLN\left( {28;56} \right)\).
Phương pháp:
Liệt kê tất cả các ước chung của 28 và 56, từ đó suy ra ước chung lớn nhất.
Lời giải:
\({\rm{U}}C\left( {28;56} \right) = \left\{ {1;2;4;7;14;28} \right\}\)
Vậy \({\rm{U}}CLN\left( {28;56} \right) = 28.\)
Bài 3: Hãy vẽ hình chữ nhật \({\rm{ABCD}}\) có độ dài cạnh \({\rm{AB}} = 4{\rm{\;cm}}\)và \({\rm{AD}} = 6{\rm{\;cm}}\). Tính chu vi và diện tích hình chữ nhật \(ABCD\).
Phương pháp:
Vẽ hình chữ nhật theo yêu cầu của đề bài. Sau đó áp dụng công thức tính chu vi, diện tích hình chữ nhật.
\(C = 2.\left( {a + b} \right)\)
\(S = a.b\)
(với \(a,b\) lần lượt là chiều dài và chiều rộng của hình chữ nhật)
Lời giải:
* Vẽ hình chữ nhật ABCD:
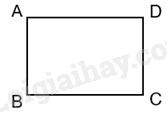
* Tính chu vi, diện tích hình chữ nhật ABCD:
Chu vi hình chữ nhật ABCD là: \(2.\left( {6 + 4} \right) = 20\left( {{\rm{cm}}} \right)\)
Diện tích hình chữ nhật ABCD là: \(6.4 = 24\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Bài 4: Hội chữ thập đỏ ở một phường dự định tặng các suất quà cho các gia đình có hoàn cảnh khó khăn trong đợt dịch Covid 19. Dự định mỗi gói quà tặng bao gồm 1 bao gạo giá 220 000 đồng/bao; 2 kg lạc giá 50 000 đồng/kg; 5 gói gia vị giá 5000 đồng/gói, 2 chai dầu ăn giá 40 000 đồng/chai. Hỏi mỗi gói quà có tổng giá trị bao nhiêu tiền?
Phương pháp:
Tính tổng giá trị của các phần quà.
Lời giải:
Tổng giá trị của mỗi gói quà là:
\(220\,000 + 2.50\,000 + 5.5\,000 + 2.40\,000 = 425\,000\)(đồng)
Bài 5: Tìm số tự nhiên \(n > 0\) sao cho \(n + 3\) chia hết cho \(n + 1\).
Phương pháp:
Sử dụng tính chất chia hết của một tổng, một hiệu.
Lời giải:
Ta có: \(n + 3 = n + 1 + 2\)
Vì \(n + 1 \vdots n + 1\) nên để \(n + 3 \vdots n + 1\) thì \(3 \vdots n + 1\)
\( \Rightarrow n + 1 \in \) Ư\(\left( 2 \right) = \left\{ {1;2} \right\}\)
\( \Rightarrow n \in \left\{ {0;\,\,1} \right\}\)
Vậy \(n \in \left\{ {0;\,\,1} \right\}.\)
Tải về
Phần trắc nghiệm
Câu 1: Tập hợp \({\rm{P}}\) các số tự nhiên lớn hơn 8 có thể viết là
A. \(P = \{ x \in N\mid x < 8\} \)
B. \(P = \{ x \in N\mid x > 8\} \)
C. \(P = \left\{ {x \in N\mid x \le 8} \right\}\)
D. \(P = \left\{ {x \in N\mid x \ge 8} \right\}\)
Câu 2: Chỉ ra cặp số tự nhiên liền trước và liền sau của số 101.
A. 100 và 102
B. 100 và 103
C. 99 và 100
D. 99 và 103
Câu 3: Số nào sau đây là số nguyên tố?
A. 2.
B. 21
C. 15.
D. 1
Câu 4: Cho tập hợp \({\rm{A}} = \left\{ {{\rm{a}};1;{\rm{b}};5} \right\}\). Chọn khẳng định đúng.
A. \(5 \in A\)
B. \(0 \in {\rm{A}}\)
C. \(1 \notin {\rm{A}}\)
D. \(a \notin A\)
Câu 5: Số nào sau đây là bội của 7?
A. 1
B. 3
C. 49
D. 16
Câu 6: Số nào sau đây là ước của 30?
A. 15.
B. 18.
C. 22.
D. 20
Câu 7: Kết quả phép tính \({6^3}.36\) là
A. \({6^3}\)
B. \({6^4}\)
C. \({6^5}\)
D. \({6^6}\)
Câu 8: U’CLN \(\left( {10;12} \right)\) là
A. 1
B. 2
C. 4
D. 12
Câu 9: Chu vi của hình tam giác đều có độ dài cạnh \(8{\rm{\;cm}}\)là
A. \(24{\rm{\;cm}}\)
B. \(24{\rm{\;c}}{{\rm{m}}^2}\)
C. \(512\,{\rm{cm}}\)
D. \(512{\rm{\;c}}{{\rm{m}}^2}\)
Câu 10: Cho hình bình hành \(ABCD\). Nhận xét đúng là
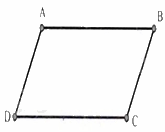
A. \(AB = AD\)
B. \(AD = BC\)
C. \({\rm{AB}} = {\rm{BC}}\)
D. \({\rm{BC}} = {\rm{CD}}\)
Phần tự luận
Bài 1: Thực hiện phép tính (bằng cách hợp lý nếu có thể):
a) \(525 + 120 + 475 + 380\)
b) \(123.35 + 66.123 - 123\)
c) \(170:\left\{ {54 - \left[ {120:4 - \left( {{4^2} - 3.2} \right)} \right]} \right\}\)
Bài 2: Tìm tất cả các ước chung của 28 và 56, từ đó tìm \({\rm{U}}CLN\left( {28;56} \right)\).
Bài 3: Hãy vẽ hình chữ nhật \({\rm{ABCD}}\) có độ dài cạnh \({\rm{AB}} = 4{\rm{\;cm}}\)và \({\rm{AD}} = 6{\rm{\;cm}}\). Tính chu vi và diện tích hình chữ nhật \(ABCD\).
Bài 4: Hội chữ thập đỏ ở một phường dự định tặng các suất quà cho các gia đình có hoàn cảnh khó khăn trong đợt dịch Covid 19. Dự định mỗi gói quà tặng bao gồm 1 bao gạo giá 220 000 đồng/bao; 2 kg lạc giá 50 000 đồng/kg; 5 gói gia vị giá 5000 đồng/gói, 2 chai dầu ăn giá 40 000 đồng/chai. Hỏi mỗi gói quà có tổng giá trị bao nhiêu tiền?
Bài 5: Tìm số tự nhiên \(n > 0\) sao cho \(n + 3\) chia hết cho \(n + 1\).
-------- Hết --------
Phần trắc nghiệm
1.B | 2.A | 3.A | 4.A | 5.C | 6.A | 7.C | 8.B | 9.A | 10.B |
Câu 1: Tập hợp \({\rm{P}}\) các số tự nhiên lớn hơn 8 có thể viết là
A. \(P = \{ x \in N\mid x < 8\} \)
B. \(P = \{ x \in N\mid x > 8\} \)
C. \(P = \left\{ {x \in N\mid x \le 8} \right\}\)
D. \(P = \left\{ {x \in N\mid x \ge 8} \right\}\)
Phương pháp:
Viết tập hợp.
Lời giải:
Tập hợp \({\rm{P}}\)các số tự nhiên lớn hơn 8 có thể viết là \(P = \{ x \in N\mid x > 8\} \).
Đáp án B.
Câu 2: Chỉ ra cặp số tự nhiên liền trước và liền sau của số 101.
A. 100 và 102
B. 100 và 103
C. 99 và 100
D. 99 và 103
Phương pháp:
Sử dụng định nghĩa số liền trước, liền sau của một số tự nhiên.
Lời giải:
Cặp số tự nhiên liền trước và liền sau của số 101 lần lượt là: 100 và 102.
Đáp án A.
Câu 3: Số nào sau đây là số nguyên tố?
A. 2.
B. 21
C. 15.
D. 1
Phương pháp:
Sử dụng khái niệm số nguyên tố.
Lời giải:
2 là số nguyên tố.
Đáp án A.
Câu 4: Cho tập hợp \({\rm{A}} = \left\{ {{\rm{a}};1;{\rm{b}};5} \right\}\). Chọn khẳng định đúng.
A. \(5 \in A\)
B. \(0 \in {\rm{A}}\)
C. \(1 \notin {\rm{A}}\)
D. \(a \notin A\)
Phương pháp:
Sử dụng kí hiệu thuộc hoặc không thuộc.
Lời giải:
\(5\) thuộc tập \(A\). Ta có: \(5 \in A\)
Đáp án A.
Câu 5: Số nào sau đây là bội của 7?
A. 1
B. 3
C. 49
D. 16
Phương pháp:
Sử dụng khái niệm bội và ước của một số nguyên:
Nếu \(a,b,x \in \mathbb{N}\) và \(a = b.x\) thì \(a \vdots b\) và a là một bội của b; b là một ước của a.
Lời giải:
49 chia hết cho 7 nên 49 là bội của 7.
Đáp án C.
Câu 6: Số nào sau đây là ước của 30?
A. 15.
B. 18.
C. 22.
D. 20
Phương pháp:
Sử dụng khái niệm bội và ước của một số nguyên:
Nếu \(a,b,x \in \mathbb{N}\) và \(a = b.x\) thì \(a \vdots b\) và a là một bội của b; b là một ước của a.
Lời giải:
30 chia hết cho 15 nên 15 là ước của 30.
Đáp án A.
Câu 7: Kết quả phép tính \({6^3}.36\) là
A. \({6^3}\)
B. \({6^4}\)
C. \({6^5}\)
D. \({6^6}\)
Phương pháp:
Viết 36 dưới dạng lũy thừa cơ số 6 rồi áp dụng công thức nhân hai lũy thừa.
\({a^m}.{a^n} = {a^{m + n}}\) (với \(a,m,n \in \mathbb{N}\))
Lời giải:
\({6^3}.36 = {6^3}{.6^2} = {6^5}\)
Đáp án C.
Câu 8: U’CLN \(\left( {10;12} \right)\) là
A. 1
B. 2
C. 4
D. 12
Phương pháp:
Vận dụng quy tắc tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Tích đó là ƯCLN phải tìm.
Lời giải:
Ta có: \(10 = 2.5;\,\,12 = {2^2}.3\)
Vậy U’CLN \(\left( {10;12} \right) = 2\)
Đáp án B.
Câu 9: Chu vi của hình tam giác đều có độ dài cạnh \(8{\rm{\;cm}}\)là
A. \(24{\rm{\;cm}}\)
B. \(24{\rm{\;c}}{{\rm{m}}^2}\)
C. \(512\,{\rm{cm}}\)
D. \(512{\rm{\;c}}{{\rm{m}}^2}\)
Phương pháp:
Chu vi tam giác đều cạnh \(a\) là: \(C = 3.a\)
Lời giải:
Chu vi của hình tam giác đều có độ dài cạnh \(8{\rm{\;cm}}\) là \(8 \times 3 = 24\left( {{\rm{cm}}} \right)\)
Đáp án A.
Câu 10: Cho hình bình hành \(ABCD\). Nhận xét đúng là
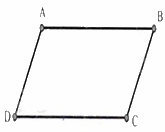
A. \(AB = AD\)
B. \(AD = BC\)
C. \({\rm{AB}} = {\rm{BC}}\)
D. \({\rm{BC}} = {\rm{CD}}\)
Phương pháp:
Nhận biết đặc điểm của hình bình hành.
Lời giải:
Hình hình hành ABCD có \(AD = BC.\)
Đáp án B.
Phần tự luận.
Bài 1: Thực hiện phép tính (bằng cách hợp lý nếu có thể):
a) \(525 + 120 + 475 + 380\)
b) \(123.35 + 66.123 - 123\)
c) \(170:\left\{ {54 - \left[ {120:4 - \left( {{4^2} - 3.2} \right)} \right]} \right\}\)
Phương pháp:
Áp dụng các quy tắc tính cộng, trừ, nhân, chia, lũy thừa.
Lời giải:
\(\begin{array}{l}a)\,\,525 + 120 + 475 + 380\\ = \left( {525 + 475} \right) + \left( {120 + 380} \right)\\ = 1000 + 500\\ = 1500\end{array}\)
\(\begin{array}{l}b)\,\,123.35 + 66.123 - 123\\ = 123.\left( {35 + 66 - 1} \right)\\ = 123.100\\ = 12300\end{array}\)
\(\begin{array}{l}c)\,\,170:\left\{ {54 - \left[ {120:4 - \left( {{4^2} - 3.2} \right)} \right]} \right\}\\ = 170:\left\{ {54 - \left[ {120:4 - \left( {16 - 6} \right)} \right]} \right\}\\ = 170:\left[ {54 - \left( {120:4 - 10} \right)} \right]\\ = 170:\left[ {54 - \left( {30 - 10} \right)} \right]\\ = 170:\left( {54 - 20} \right)\\ = 170:34\\ = 5\end{array}\)
Bài 2: Tìm tất cả các ước chung của 28 và 56, từ đó tìm \({\rm{U}}CLN\left( {28;56} \right)\).
Phương pháp:
Liệt kê tất cả các ước chung của 28 và 56, từ đó suy ra ước chung lớn nhất.
Lời giải:
\({\rm{U}}C\left( {28;56} \right) = \left\{ {1;2;4;7;14;28} \right\}\)
Vậy \({\rm{U}}CLN\left( {28;56} \right) = 28.\)
Bài 3: Hãy vẽ hình chữ nhật \({\rm{ABCD}}\) có độ dài cạnh \({\rm{AB}} = 4{\rm{\;cm}}\)và \({\rm{AD}} = 6{\rm{\;cm}}\). Tính chu vi và diện tích hình chữ nhật \(ABCD\).
Phương pháp:
Vẽ hình chữ nhật theo yêu cầu của đề bài. Sau đó áp dụng công thức tính chu vi, diện tích hình chữ nhật.
\(C = 2.\left( {a + b} \right)\)
\(S = a.b\)
(với \(a,b\) lần lượt là chiều dài và chiều rộng của hình chữ nhật)
Lời giải:
* Vẽ hình chữ nhật ABCD:
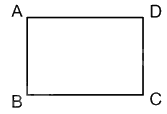
* Tính chu vi, diện tích hình chữ nhật ABCD:
Chu vi hình chữ nhật ABCD là: \(2.\left( {6 + 4} \right) = 20\left( {{\rm{cm}}} \right)\)
Diện tích hình chữ nhật ABCD là: \(6.4 = 24\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Bài 4: Hội chữ thập đỏ ở một phường dự định tặng các suất quà cho các gia đình có hoàn cảnh khó khăn trong đợt dịch Covid 19. Dự định mỗi gói quà tặng bao gồm 1 bao gạo giá 220 000 đồng/bao; 2 kg lạc giá 50 000 đồng/kg; 5 gói gia vị giá 5000 đồng/gói, 2 chai dầu ăn giá 40 000 đồng/chai. Hỏi mỗi gói quà có tổng giá trị bao nhiêu tiền?
Phương pháp:
Tính tổng giá trị của các phần quà.
Lời giải:
Tổng giá trị của mỗi gói quà là:
\(220\,000 + 2.50\,000 + 5.5\,000 + 2.40\,000 = 425\,000\)(đồng)
Bài 5: Tìm số tự nhiên \(n > 0\) sao cho \(n + 3\) chia hết cho \(n + 1\).
Phương pháp:
Sử dụng tính chất chia hết của một tổng, một hiệu.
Lời giải:
Ta có: \(n + 3 = n + 1 + 2\)
Vì \(n + 1 \vdots n + 1\) nên để \(n + 3 \vdots n + 1\) thì \(3 \vdots n + 1\)
\( \Rightarrow n + 1 \in \) Ư\(\left( 2 \right) = \left\{ {1;2} \right\}\)
\( \Rightarrow n \in \left\{ {0;\,\,1} \right\}\)
Vậy \(n \in \left\{ {0;\,\,1} \right\}.\)
Đề thi giữa kì 1 Toán 6 - Đề số 11 đóng vai trò quan trọng trong việc đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kỳ đầu tiên. Đề thi thường bao gồm các dạng bài tập thuộc các chủ đề chính đã được học, như số tự nhiên, phép tính với số tự nhiên, hình học cơ bản và các bài toán thực tế liên quan.
Thông thường, đề thi giữa kì 1 Toán 6 - Đề số 11 có cấu trúc gồm:
Tỷ lệ điểm giữa phần trắc nghiệm và tự luận có thể khác nhau tùy theo quy định của từng trường.
Các chủ đề thường xuất hiện trong đề thi giữa kì 1 Toán 6 - Đề số 11 bao gồm:
Để đạt kết quả tốt trong đề thi giữa kì 1 Toán 6 - Đề số 11, học sinh cần:
Bài toán: Tính giá trị của biểu thức: 123 + 456 - 789
Giải:
Ngoài việc làm đề thi giữa kì 1 Toán 6 - Đề số 11, học sinh có thể tham khảo thêm các tài liệu ôn tập và luyện thi sau:
Hãy dành thời gian ôn tập và luyện tập đều đặn để chuẩn bị tốt nhất cho đề thi giữa kì 1 Toán 6 - Đề số 11. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn trong quá trình học tập. Chúc các em đạt kết quả tốt!
| Dạng bài tập | Ví dụ |
|---|---|
| Tính giá trị biểu thức | 25 + 35 x 2 |
| Tìm x | x + 15 = 30 |
| Bài toán chia hết | Số nào sau đây chia hết cho 3: 12, 15, 17 |