Chào mừng các em học sinh đến với đề thi giữa kì 2 Toán 6 - Đề số 5 chương trình Kết nối tri thức. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì 2.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học và kiểm tra kết quả một cách hiệu quả. Chúc các em làm bài tốt!
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho điểm \(E\) nằm giữa hai điểm \(I\) và \(K\), biết \(IE = 4cm,\,\,EK = 10cm\). Độ dài \(IK\) là:
A.\(4\,cm\)
B.\(7\,cm\)
C. \(14\,cm\)
D. \(6\,cm\)
Câu 2: Cho \(I\) là trung điểm của đoạn thẳng \(MN\). Biết\(NI = 8cm\), khi đó độ dài \(MN\) là
A.\(4\,cm\)
B. \(16\,cm\)
C. \(21\,cm\)
D. \(24\,cm\)
Câu 3: Giá trị của phép tính: \(\dfrac{1}{4} + \left( {\dfrac{{ - 1}}{2} + \dfrac{2}{3}} \right)\) bằng:
A. \(\dfrac{3}{{12}}\)
B. \(\dfrac{4}{{12}}\)
C. \(\dfrac{5}{{12}}\)
D. \(\dfrac{6}{{12}}\)
Câu 4:Hỗn số \( - 3\dfrac{2}{5}\) viết dưới dạng phân số là:
A. \(\dfrac{{ - 17}}{5};\)
B.\(\dfrac{{17}}{5}\)
C.\( - \dfrac{6}{5};\)
D.\( - \dfrac{{13}}{5}.\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể):
\(a)\,\dfrac{7}{{15}} + \dfrac{6}{5}\)
\(b)\, - 1,8:\left( {1 - \dfrac{7}{{10}}} \right)\)
\(c)\,\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\(a)\,x - 1\dfrac{2}{5} = \dfrac{3}{4}\)
\(b)\,\dfrac{1}{2}x - \dfrac{4}{7} = 1\dfrac{3}{7}\)
\(c)\,\,\dfrac{2}{3}x - \dfrac{3}{2}\left( {x - \dfrac{1}{2}} \right) = \dfrac{5}{{12}}\)
Bài 3 (1,5 điểm) Một mảnh vườn hình chữ nhật có chiều dài \(60m\), chiều rộng bằng \(\dfrac{2}{3}\) chiều dài.
a) Tính diện tích mảnh vườn.
b) Người ta lấy \(\dfrac{3}{5}\) diện tích mảnh vườn để trồng cây, \(\dfrac{3}{{20}}\) diện tích phần vườn còn lại dùng để nuôi gà. Tính diện tích phần vườn dùng để nuôi gà?
Bài 4: (2,5 điểm) Cho đường thẳng \(xy\). Lấy điểm \(O\) thuộc đường thẳng \(xy\). Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA = 3cm\). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(AB = 6cm\).
a) Kể tên các cặp tia đối nhau gốc \(A\) đến hình vẽ?
b) Tính độ dài đoạn thẳng \(OB\).
c) Điểm \(O\) có là trung điểm của đoạn thẳng \(AB\) không? Vì sao?
Bài 5:(0,5 điểm)Cho \(A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2014}^2}}}\). Chứng tỏ: \(A < \dfrac{3}{4}\).
Phần I: Trắc nghiệm
1. D | 2. B | 3. C | 4. A |
Câu 1
Phương pháp:
Điểm \(E\) nằm giữa hai điểm \(I\) và \(K\) thì \(IE + IK = EK\).
Cách giải:
Vì điểm \(E\) nằm giữa hai điểm \(I\) và \(K\) nên ta có: \(IE + IK = EK\)
\( \Rightarrow IK = EK - IE\)\( = 10cm - 4cm = 6cm\)
Vậy độ dài \(IK\) là \(6cm\).
Chọn D.
Câu 2
Phương pháp:
\(I\) là trung điểm của đoạn thẳng \(MN\) thì \(IM = IN = \dfrac{{MN}}{2}\).
Cách giải:
Vì \(I\) là trung điểm của đoạn thẳng \(MN\) nên \(IM = IN = \dfrac{{MN}}{2}\)
\( \Rightarrow MN = 2.IN = 2.8cm = 16cm\).
Vậy \(MN = 16cm\).
Chọn B.
Câu 3
Phương pháp:
Áp dụng quy tắc bỏ ngoặc
Thực hiện phép cộng phân số có cùng mẫu số.
Cách giải:
\(\dfrac{1}{4} + \left( {\dfrac{{ - 1}}{2} + \dfrac{2}{3}} \right)\)
\(\begin{array}{l} = \dfrac{1}{4} + \dfrac{{ - 1}}{2} + \dfrac{2}{3}\\ = \dfrac{{1.3}}{{12}} + \dfrac{{\left( { - 1} \right).6}}{{12}} + \dfrac{{2.4}}{{12}}\\ = \dfrac{{3 + \left( { - 6} \right) + 8}}{{12}}\\ = \dfrac{5}{{12}}\end{array}\)
Chọn C.
Câu 4
Phương pháp:
Muốn viết hỗn số về dạng phân số ta lấy phần nguyên nhân với mẫu số của phần phân số rồi cộng với tử số của phần phân số làm tử số, mẫu số là mẫu số của phần phân số.
Tổng quát: \(a\dfrac{b}{c} = a + \dfrac{b}{c}\) Cách giải:
Ta có: \( - 3\dfrac{2}{5} = - \dfrac{{5.3 + 2}}{5} = - \dfrac{{17}}{5}\)
Chọn A
Phần II: Tự luận
Bài 1
Phương pháp
a) Thực hiện cộng hai phân số khác mẫu, ta quy đồng mẫu số hai phân số đó, rồi cộng tử với tử và giữ nguyên mẫu.
b) Nhận thấy số chia là một phân số có mẫu số là 10, ta chuyển \( - 1,8\) về dạng phân số có mẫu số là 10. Sau đó thự hiện chia hai phân số. Muốn chia hai phân số ta lấy số bị chia nhân với phân số nghịch đảo của số chia.
c) Sử dụng tính chất phân phối của phép nhân đối với phép cộng :
\(a.b + a.c + a.d = a.\left( {b + c + d} \right)\)
Cách giải:
\(a)\,\dfrac{7}{{15}} + \dfrac{6}{5} = \dfrac{7}{{15}} + \dfrac{{18}}{{15}} = \dfrac{{25}}{{15}} = \dfrac{5}{3}\)
\(b)\, - 1,8:\left( {1 - \dfrac{7}{{10}}} \right) = \dfrac{{ - 18}}{{10}}:\dfrac{3}{{10}} = \dfrac{{ - 18}}{{10}}.\dfrac{{10}}{3} = - 6\)
\(\begin{array}{l}c)\,\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\\\,\,\,\,\, = \dfrac{{ - 5}}{7}.\left( {\dfrac{2}{{13}} + \dfrac{3}{{13}} + \dfrac{8}{{13}}} \right)\\\,\,\,\, = \dfrac{{ - 5}}{7}.\,1\\\,\,\, = \dfrac{{ - 5}}{7}\end{array}\)
Bài 2:
Phương pháp: a) Đổi hỗn số về phân số, rồi thực hiện quy tắc chuyển vế, chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu, rồi thực hiện phép cộng hai phân số khác mẫu, muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số của hai phân số đó rồi thực hiện cộng tử với tử, mẫu số giữ nguyên.
b) Chuyển hỗn số về phân số, rồi thực hiện chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu. Sau đó, thực hiện cộng hai phân số có cùng mẫu số (ta cộng tử với tử, giữ nguyên mẫu).
Để tìm x ta lấy kết quả cộng hai phân số chia cho \(\dfrac{1}{2}\).
Cách giải:
\(\begin{array}{l}a)\,x - 1\dfrac{2}{5} = \dfrac{3}{4}\\\,\,\,\,\,x\, - \,\dfrac{7}{5} = \dfrac{3}{4}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{4} + \dfrac{7}{5}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{{43}}{{20}}\end{array}\)
Vậy \(x = \dfrac{{43}}{{20}}\)
\(\begin{array}{l}b)\,\dfrac{1}{2}x - \dfrac{4}{7} = 1\dfrac{3}{7}\\\,\,\,\,\,\dfrac{1}{2}x - \dfrac{4}{7} = \dfrac{{10}}{7}\\\,\,\,\,\,\dfrac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \dfrac{{10}}{7} + \dfrac{4}{7}\\\,\,\,\,\,\dfrac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \dfrac{{14}}{7}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{{14}}{7}:\dfrac{1}{2}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = 4\end{array}\)
Vậy \(x = 4\)
\(\begin{array}{l}c)\,\,\dfrac{2}{3}x - \dfrac{3}{2}\left( {x - \dfrac{1}{2}} \right)\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\dfrac{2}{3}x - \left( {\dfrac{3}{2}x - \dfrac{3}{2} \cdot \dfrac{1}{2}} \right) = \dfrac{5}{{12}}\\\,\,\,\,\,\,\dfrac{2}{3}x - \dfrac{3}{2}x + \dfrac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x + \dfrac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}} - \dfrac{3}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{3}:\dfrac{{ - 5}}{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\dfrac{2}{5}\end{array}\)
Vậy \(x = \dfrac{2}{5}\)
Bài 3
Phương pháp:
- Vận dụng quy tắc tìm giá trị phân số của một số cho trước
Cách giải:
Chiều rộng của mảnh vườn là: \(60.\dfrac{2}{3} = 40\) \(\left( m \right)\)
a) Diện tích của mảnh vườn là: \(60.40 = 2400\left( {{m^2}} \right)\)
b) Diện tích phần vườn trồng cây là: \(2400.\dfrac{3}{5} = 1440\left( {{m^2}} \right)\)
Diện tích phần vườn còn lại là: \(2400 - 1440 = 960\left( {{m^2}} \right)\)
Diện tích phần vườn nuôi gà là: \(960.\dfrac{3}{{20}} = 144\left( {{m^2}} \right)\)
Bài 4
Phương pháp:
a) Áp dụng định nghĩa hai tia đối nhau: Hai tia đối nhau có chung gốc và chúng tạo thành một đường thẳng.
b) Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\) thì \(OA + OB = AB\).
c) Điểm \(O\) là trung điểm của đoạn thẳng \(AB\) nếu: Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\); \(OA = OB\)
Cách giải:
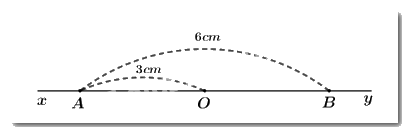
a) Kể tên các cặp tia đối nhau gốc \(A\) đến hình vẽ?
Các cặp tia đối nhau gốc \(A\) là: \(Ax\) và \(AO\); \(Ax\) và \(AB\); \(Ax\) và \(Ay\)
b) Tính độ dài đoạn thẳng \(OB\).
Ta có:
+ Điểm \(O\) thuộc đường thẳng \(xy\) nên \(Ox\) và \(Oy\) thuộc hai tia đối nhau.
+ \(A \in Ox\)
+ \(B \in Oy\)
Suy ra, điểm \(O\) nằm giữa hai điểm \(A\) và \(B\).
Khi đó, ta có: \(OA + OB = AB\)
\( \Rightarrow OB = AB - OA\)\( = 6\,cm - 3\,cm = 3\,cm\)
Vậy \(OB = 3cm\).
c) Điểm \(O\) có là trung điểm của đoạn thẳng \(AB\) không? Vì sao?
Ta có:
+ Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\).
+ \(OA = OB = 3cm\)
Suy ra, điểm \(O\) là trung điểm của đoạn thẳng \(AB\).
Bài 5
Phương pháp:
Áp dụng bất đẳng thức: \(\dfrac{1}{{{n^2}}} < \dfrac{1}{{\left( {n - 1} \right).n}}\) với \(n \in {\mathbb{N}^*},\,\,n > 1\) và đẳng thức: \(\dfrac{1}{{n\left( {n - 1} \right)}} = \dfrac{1}{{n - 1}} - \dfrac{1}{n}.\)
Cách giải:
Ta có :
\(\begin{array}{l}A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2014}^2}}}\\A = \dfrac{1}{4} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{2014.2014}}\\A < \dfrac{1}{4} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{2013.2014}}\\A < \dfrac{1}{4} + \left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{2013}} - \dfrac{1}{{2014}}} \right)\\A < \dfrac{1}{4} + \dfrac{1}{2} - \dfrac{1}{{2014}}\\A < \dfrac{3}{4} - \dfrac{1}{{2014}}\\ \Rightarrow A < \dfrac{3}{4}\end{array}\)
Vậy \(A < \dfrac{3}{4}\).
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho điểm \(E\) nằm giữa hai điểm \(I\) và \(K\), biết \(IE = 4cm,\,\,EK = 10cm\). Độ dài \(IK\) là:
A.\(4\,cm\)
B.\(7\,cm\)
C. \(14\,cm\)
D. \(6\,cm\)
Câu 2: Cho \(I\) là trung điểm của đoạn thẳng \(MN\). Biết\(NI = 8cm\), khi đó độ dài \(MN\) là
A.\(4\,cm\)
B. \(16\,cm\)
C. \(21\,cm\)
D. \(24\,cm\)
Câu 3: Giá trị của phép tính: \(\dfrac{1}{4} + \left( {\dfrac{{ - 1}}{2} + \dfrac{2}{3}} \right)\) bằng:
A. \(\dfrac{3}{{12}}\)
B. \(\dfrac{4}{{12}}\)
C. \(\dfrac{5}{{12}}\)
D. \(\dfrac{6}{{12}}\)
Câu 4:Hỗn số \( - 3\dfrac{2}{5}\) viết dưới dạng phân số là:
A. \(\dfrac{{ - 17}}{5};\)
B.\(\dfrac{{17}}{5}\)
C.\( - \dfrac{6}{5};\)
D.\( - \dfrac{{13}}{5}.\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể):
\(a)\,\dfrac{7}{{15}} + \dfrac{6}{5}\)
\(b)\, - 1,8:\left( {1 - \dfrac{7}{{10}}} \right)\)
\(c)\,\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\(a)\,x - 1\dfrac{2}{5} = \dfrac{3}{4}\)
\(b)\,\dfrac{1}{2}x - \dfrac{4}{7} = 1\dfrac{3}{7}\)
\(c)\,\,\dfrac{2}{3}x - \dfrac{3}{2}\left( {x - \dfrac{1}{2}} \right) = \dfrac{5}{{12}}\)
Bài 3 (1,5 điểm) Một mảnh vườn hình chữ nhật có chiều dài \(60m\), chiều rộng bằng \(\dfrac{2}{3}\) chiều dài.
a) Tính diện tích mảnh vườn.
b) Người ta lấy \(\dfrac{3}{5}\) diện tích mảnh vườn để trồng cây, \(\dfrac{3}{{20}}\) diện tích phần vườn còn lại dùng để nuôi gà. Tính diện tích phần vườn dùng để nuôi gà?
Bài 4: (2,5 điểm) Cho đường thẳng \(xy\). Lấy điểm \(O\) thuộc đường thẳng \(xy\). Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA = 3cm\). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(AB = 6cm\).
a) Kể tên các cặp tia đối nhau gốc \(A\) đến hình vẽ?
b) Tính độ dài đoạn thẳng \(OB\).
c) Điểm \(O\) có là trung điểm của đoạn thẳng \(AB\) không? Vì sao?
Bài 5:(0,5 điểm)Cho \(A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2014}^2}}}\). Chứng tỏ: \(A < \dfrac{3}{4}\).
Phần I: Trắc nghiệm
1. D | 2. B | 3. C | 4. A |
Câu 1
Phương pháp:
Điểm \(E\) nằm giữa hai điểm \(I\) và \(K\) thì \(IE + IK = EK\).
Cách giải:
Vì điểm \(E\) nằm giữa hai điểm \(I\) và \(K\) nên ta có: \(IE + IK = EK\)
\( \Rightarrow IK = EK - IE\)\( = 10cm - 4cm = 6cm\)
Vậy độ dài \(IK\) là \(6cm\).
Chọn D.
Câu 2
Phương pháp:
\(I\) là trung điểm của đoạn thẳng \(MN\) thì \(IM = IN = \dfrac{{MN}}{2}\).
Cách giải:
Vì \(I\) là trung điểm của đoạn thẳng \(MN\) nên \(IM = IN = \dfrac{{MN}}{2}\)
\( \Rightarrow MN = 2.IN = 2.8cm = 16cm\).
Vậy \(MN = 16cm\).
Chọn B.
Câu 3
Phương pháp:
Áp dụng quy tắc bỏ ngoặc
Thực hiện phép cộng phân số có cùng mẫu số.
Cách giải:
\(\dfrac{1}{4} + \left( {\dfrac{{ - 1}}{2} + \dfrac{2}{3}} \right)\)
\(\begin{array}{l} = \dfrac{1}{4} + \dfrac{{ - 1}}{2} + \dfrac{2}{3}\\ = \dfrac{{1.3}}{{12}} + \dfrac{{\left( { - 1} \right).6}}{{12}} + \dfrac{{2.4}}{{12}}\\ = \dfrac{{3 + \left( { - 6} \right) + 8}}{{12}}\\ = \dfrac{5}{{12}}\end{array}\)
Chọn C.
Câu 4
Phương pháp:
Muốn viết hỗn số về dạng phân số ta lấy phần nguyên nhân với mẫu số của phần phân số rồi cộng với tử số của phần phân số làm tử số, mẫu số là mẫu số của phần phân số.
Tổng quát: \(a\dfrac{b}{c} = a + \dfrac{b}{c}\) Cách giải:
Ta có: \( - 3\dfrac{2}{5} = - \dfrac{{5.3 + 2}}{5} = - \dfrac{{17}}{5}\)
Chọn A
Phần II: Tự luận
Bài 1
Phương pháp
a) Thực hiện cộng hai phân số khác mẫu, ta quy đồng mẫu số hai phân số đó, rồi cộng tử với tử và giữ nguyên mẫu.
b) Nhận thấy số chia là một phân số có mẫu số là 10, ta chuyển \( - 1,8\) về dạng phân số có mẫu số là 10. Sau đó thự hiện chia hai phân số. Muốn chia hai phân số ta lấy số bị chia nhân với phân số nghịch đảo của số chia.
c) Sử dụng tính chất phân phối của phép nhân đối với phép cộng :
\(a.b + a.c + a.d = a.\left( {b + c + d} \right)\)
Cách giải:
\(a)\,\dfrac{7}{{15}} + \dfrac{6}{5} = \dfrac{7}{{15}} + \dfrac{{18}}{{15}} = \dfrac{{25}}{{15}} = \dfrac{5}{3}\)
\(b)\, - 1,8:\left( {1 - \dfrac{7}{{10}}} \right) = \dfrac{{ - 18}}{{10}}:\dfrac{3}{{10}} = \dfrac{{ - 18}}{{10}}.\dfrac{{10}}{3} = - 6\)
\(\begin{array}{l}c)\,\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\\\,\,\,\,\, = \dfrac{{ - 5}}{7}.\left( {\dfrac{2}{{13}} + \dfrac{3}{{13}} + \dfrac{8}{{13}}} \right)\\\,\,\,\, = \dfrac{{ - 5}}{7}.\,1\\\,\,\, = \dfrac{{ - 5}}{7}\end{array}\)
Bài 2:
Phương pháp: a) Đổi hỗn số về phân số, rồi thực hiện quy tắc chuyển vế, chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu, rồi thực hiện phép cộng hai phân số khác mẫu, muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số của hai phân số đó rồi thực hiện cộng tử với tử, mẫu số giữ nguyên.
b) Chuyển hỗn số về phân số, rồi thực hiện chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu. Sau đó, thực hiện cộng hai phân số có cùng mẫu số (ta cộng tử với tử, giữ nguyên mẫu).
Để tìm x ta lấy kết quả cộng hai phân số chia cho \(\dfrac{1}{2}\).
Cách giải:
\(\begin{array}{l}a)\,x - 1\dfrac{2}{5} = \dfrac{3}{4}\\\,\,\,\,\,x\, - \,\dfrac{7}{5} = \dfrac{3}{4}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{4} + \dfrac{7}{5}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{{43}}{{20}}\end{array}\)
Vậy \(x = \dfrac{{43}}{{20}}\)
\(\begin{array}{l}b)\,\dfrac{1}{2}x - \dfrac{4}{7} = 1\dfrac{3}{7}\\\,\,\,\,\,\dfrac{1}{2}x - \dfrac{4}{7} = \dfrac{{10}}{7}\\\,\,\,\,\,\dfrac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \dfrac{{10}}{7} + \dfrac{4}{7}\\\,\,\,\,\,\dfrac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \dfrac{{14}}{7}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{{14}}{7}:\dfrac{1}{2}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = 4\end{array}\)
Vậy \(x = 4\)
\(\begin{array}{l}c)\,\,\dfrac{2}{3}x - \dfrac{3}{2}\left( {x - \dfrac{1}{2}} \right)\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\dfrac{2}{3}x - \left( {\dfrac{3}{2}x - \dfrac{3}{2} \cdot \dfrac{1}{2}} \right) = \dfrac{5}{{12}}\\\,\,\,\,\,\,\dfrac{2}{3}x - \dfrac{3}{2}x + \dfrac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x + \dfrac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}} - \dfrac{3}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{3}:\dfrac{{ - 5}}{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\dfrac{2}{5}\end{array}\)
Vậy \(x = \dfrac{2}{5}\)
Bài 3
Phương pháp:
- Vận dụng quy tắc tìm giá trị phân số của một số cho trước
Cách giải:
Chiều rộng của mảnh vườn là: \(60.\dfrac{2}{3} = 40\) \(\left( m \right)\)
a) Diện tích của mảnh vườn là: \(60.40 = 2400\left( {{m^2}} \right)\)
b) Diện tích phần vườn trồng cây là: \(2400.\dfrac{3}{5} = 1440\left( {{m^2}} \right)\)
Diện tích phần vườn còn lại là: \(2400 - 1440 = 960\left( {{m^2}} \right)\)
Diện tích phần vườn nuôi gà là: \(960.\dfrac{3}{{20}} = 144\left( {{m^2}} \right)\)
Bài 4
Phương pháp:
a) Áp dụng định nghĩa hai tia đối nhau: Hai tia đối nhau có chung gốc và chúng tạo thành một đường thẳng.
b) Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\) thì \(OA + OB = AB\).
c) Điểm \(O\) là trung điểm của đoạn thẳng \(AB\) nếu: Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\); \(OA = OB\)
Cách giải:
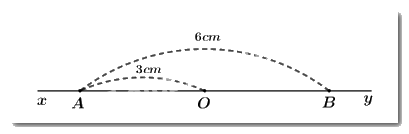
a) Kể tên các cặp tia đối nhau gốc \(A\) đến hình vẽ?
Các cặp tia đối nhau gốc \(A\) là: \(Ax\) và \(AO\); \(Ax\) và \(AB\); \(Ax\) và \(Ay\)
b) Tính độ dài đoạn thẳng \(OB\).
Ta có:
+ Điểm \(O\) thuộc đường thẳng \(xy\) nên \(Ox\) và \(Oy\) thuộc hai tia đối nhau.
+ \(A \in Ox\)
+ \(B \in Oy\)
Suy ra, điểm \(O\) nằm giữa hai điểm \(A\) và \(B\).
Khi đó, ta có: \(OA + OB = AB\)
\( \Rightarrow OB = AB - OA\)\( = 6\,cm - 3\,cm = 3\,cm\)
Vậy \(OB = 3cm\).
c) Điểm \(O\) có là trung điểm của đoạn thẳng \(AB\) không? Vì sao?
Ta có:
+ Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\).
+ \(OA = OB = 3cm\)
Suy ra, điểm \(O\) là trung điểm của đoạn thẳng \(AB\).
Bài 5
Phương pháp:
Áp dụng bất đẳng thức: \(\dfrac{1}{{{n^2}}} < \dfrac{1}{{\left( {n - 1} \right).n}}\) với \(n \in {\mathbb{N}^*},\,\,n > 1\) và đẳng thức: \(\dfrac{1}{{n\left( {n - 1} \right)}} = \dfrac{1}{{n - 1}} - \dfrac{1}{n}.\)
Cách giải:
Ta có :
\(\begin{array}{l}A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2014}^2}}}\\A = \dfrac{1}{4} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{2014.2014}}\\A < \dfrac{1}{4} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{2013.2014}}\\A < \dfrac{1}{4} + \left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{2013}} - \dfrac{1}{{2014}}} \right)\\A < \dfrac{1}{4} + \dfrac{1}{2} - \dfrac{1}{{2014}}\\A < \dfrac{3}{4} - \dfrac{1}{{2014}}\\ \Rightarrow A < \dfrac{3}{4}\end{array}\)
Vậy \(A < \dfrac{3}{4}\).
Đề thi giữa kì 2 Toán 6 - Đề số 5 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kì. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã được học, như số tự nhiên, phân số, số thập phân, hình học cơ bản và các bài toán thực tế.
Thông thường, đề thi giữa kì 2 Toán 6 - Đề số 5 - Kết nối tri thức sẽ có cấu trúc tương tự như sau:
Để chuẩn bị tốt nhất cho đề thi giữa kì 2 Toán 6 - Đề số 5 - Kết nối tri thức, học sinh cần nắm vững các kiến thức sau:
Dưới đây là hướng dẫn giải một số dạng bài tập thường gặp trong đề thi giữa kì 2 Toán 6 - Đề số 5 - Kết nối tri thức:
Để tính toán các biểu thức số học, học sinh cần nắm vững thứ tự thực hiện các phép tính (nhân, chia trước; cộng, trừ sau). Sử dụng dấu ngoặc để thay đổi thứ tự thực hiện các phép tính khi cần thiết.
Để giải các bài toán về phân số, học sinh cần nắm vững các quy tắc về cộng, trừ, nhân, chia phân số. Quy đồng mẫu số trước khi cộng hoặc trừ các phân số. Chú ý đến việc rút gọn phân số sau khi thực hiện các phép tính.
Để giải các bài toán về số thập phân, học sinh cần nắm vững các quy tắc về cộng, trừ, nhân, chia số thập phân. Đặt các số thập phân sao cho các chữ số ở cùng một hàng thẳng hàng trước khi thực hiện các phép tính.
Để giải các bài toán về hình học, học sinh cần nắm vững các công thức tính diện tích và chu vi của các hình. Vẽ hình minh họa để dễ dàng hình dung bài toán và tìm ra lời giải.
Giaitoan.edu.vn là một website cung cấp các tài liệu học tập Toán 6 uy tín, bao gồm đề thi, bài tập, đáp án và các bài giảng online. Chúng tôi hy vọng rằng các tài liệu này sẽ giúp các em học sinh học tập Toán 6 một cách hiệu quả và đạt kết quả tốt nhất.