Bài học Toán lớp 5 Bài 4: Ôn tập và bổ sung về phân số - SGK Cánh Diều là một phần quan trọng trong chương trình học Toán 5, giúp học sinh củng cố kiến thức về phân số đã học và mở rộng thêm các kiến thức mới.
Tại giaitoan.edu.vn, chúng tôi cung cấp đầy đủ các bài giải chi tiết, dễ hiểu, cùng với các video hướng dẫn và bài tập luyện tập để giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập về phân số.
a) Viết phân số chỉ số phần đã tô màu trong mỗi hình rồi đọc (theo mẫu) ... Quy đồng mẫu số hai phân số 3/14 và 4/7
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 13 SGK Toán 5 Cánh diều
a) Nêu hai phân số bằng mỗi phân số sau: $\frac{5}{4};\,\frac{9}{{12}}$.
b) Rút gọn các phân số sau: $\frac{{24}}{{32}};\,\,\frac{{14}}{{35}};\,\,\frac{{30}}{{25}};\,\,\frac{{63}}{{36}}$
Phương pháp giải:
a) Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
b) Rút gọn phân số:
• Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
• Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
a) \(\frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}}\) ; \(\frac{5}{4} = \frac{{5 \times 5}}{{4 \times 5}} = \frac{{25}}{{20}}\)
Hai phân số bằng phân số $\frac{5}{4}$là $\frac{{15}}{{12}}$và $\frac{{25}}{{20}}$
\(\frac{9}{{12}} = \frac{{9:3}}{{12:3}} = \frac{3}{4}\) ; \(\frac{9}{{12}} = \frac{{9 \times 2}}{{12 \times 2}} = \frac{{18}}{{24}}\)
Hai phân số bằng phân số $\frac{9}{{12}}$là $\frac{3}{4}$và $\frac{{18}}{{24}}$
b) $\frac{{24}}{{32}} = \frac{{24:8}}{{32:8}} = \frac{3}{4}$
$\frac{{14}}{{35}} = \frac{{14:7}}{{35:7}} = \frac{2}{5}$
$\frac{{30}}{{25}} = \frac{{30:5}}{{25:5}} = \frac{6}{5}$
$\frac{{63}}{{36}} = \frac{{63:9}}{{36:9}} = \frac{7}{4}$
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 13 SGK Toán 5 Cánh diều
Quy đồng mẫu số hai phân số:

Phương pháp giải:
- Tìm mẫu số chung- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
a) $\frac{4}{7} = \frac{{4 \times 2}}{{7 \times 2}} = \frac{8}{{14}}$; giữ nguyên phân số $\frac{3}{{14}}$.
Vậy quy đồng mẫu số hai phân số $\frac{3}{{14}}$và $\frac{4}{7}$ta được $\frac{3}{{14}}$và $\frac{8}{{14}}$.
b) $\frac{2}{3} = \frac{{2 \times 2}}{{3 \times 2}} = \frac{4}{6}$; giữ nguyên phân số $\frac{5}{6}$.
Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$và $\frac{5}{6}$ta được $\frac{4}{6}$và $\frac{5}{6}$.
Video hướng dẫn giải
Trả lời câu hỏi 5 trang 13 SGK Toán 5 Cánh diều
a) Đọc ví dụ sau rồi nói cho bạn nghe cách thực hiện:
Ví dụ: Quy đồng mẫu số hai phân số $\frac{2}{3}$và $\frac{5}{4}$
Vì 3 x 4 = 12 nên ta chọn 12 làm mẫu số chung.
Ta có: $\frac{2}{3} = \frac{{2 \times 4}}{{3 \times 4}} = \frac{8}{{12}}$ và $\frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}}$
Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$và $\frac{5}{4}$ta được $\frac{8}{{12}}$và $\frac{{15}}{{12}}$
b) Quy đồng mẫu số hai phân số:
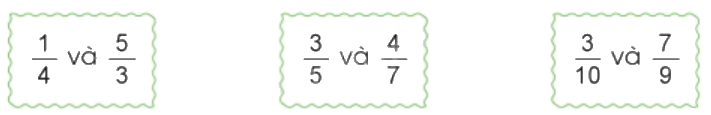
Phương pháp giải:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Lời giải chi tiết:
a) Cách quy đồng mẫu số:
- Chọn mẫu số chung
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
b)
$\frac{1}{4}$và $\frac{5}{3}$
Vì 4 x 3 = 12 nên ta chọn 12 làm mẫu số chung.
Ta có: \(\frac{1}{4} = \frac{{1 \times 3}}{{4 \times 3}} = \frac{3}{{12}}\) và $\frac{5}{3} = \frac{{5 \times 4}}{{3 \times 4}} = \frac{{20}}{{12}}$
Vậy quy đồng mẫu số hai phân số $\frac{1}{4}$và $\frac{5}{3}$ta được $\frac{3}{{12}}$và $\frac{{20}}{{12}}$.
$\frac{3}{5}$và $\frac{4}{7}$
Vì 5 x 7 = 35 nên ta chọn 35 làm mẫu số chung.
Ta có: \(\frac{3}{5} = \frac{{3 \times 7}}{{5 \times 7}} = \frac{{21}}{{35}}\) và $\frac{4}{7} = \frac{{4 \times 5}}{{7 \times 5}} = \frac{{20}}{{35}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{5}$và $\frac{4}{7}$ta được $\frac{{21}}{{35}}$và $\frac{{20}}{{35}}$.
$\frac{3}{{10}}$và $\frac{7}{9}$
Vì 10 x 9 = 90 nên ta chọn 90 làm mẫu số chung.
Ta có: \(\frac{3}{{10}} = \frac{{3 \times 9}}{{10 \times 9}} = \frac{{27}}{{90}}\) và $\frac{7}{9} = \frac{{7 \times 10}}{{9 \times 10}} = \frac{{70}}{{90}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{{10}}$và $\frac{7}{9}$ta được $\frac{{27}}{{90}}$và $\frac{{70}}{{90}}$
Video hướng dẫn giải
Trả lời câu hỏi 6 trang 14 SGK Toán 5 Cánh diều
Quy đồng mẫu số hai phân số:

Phương pháp giải:
- Tìm mẫu số chung
- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
+) $\frac{3}{4}$và $\frac{1}{6}$
Chọn 12 làm mẫu số chung.
Ta có: $\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$ và $\frac{1}{6} = \frac{{1 \times 2}}{{6 \times 2}} = \frac{2}{{12}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{4}$và $\frac{1}{6}$ ta được $\frac{9}{{12}}$và $\frac{2}{{12}}$.
+) $\frac{7}{{10}}$ và $\frac{5}{8}$
Chọn 40 làm mẫu số chung.
Ta có: $\frac{7}{{10}} = \frac{{7 \times 4}}{{10 \times 4}} = \frac{{28}}{{40}}$ và $\frac{5}{8} = \frac{{5 \times 5}}{{8 \times 5}} = \frac{{25}}{{40}}$
Vậy quy đồng mẫu số hai phân số $\frac{7}{{10}}$và $\frac{5}{8}$ ta được $\frac{{28}}{{40}}$và $\frac{{25}}{{40}}$.
+) $\frac{4}{9}$ và $\frac{5}{{16}}$
Chọn 144 làm mẫu số chung.
Ta có: \(\frac{4}{9} = \frac{{4 \times 16}}{{9 \times 16}} = \frac{{64}}{{144}}\) và $\frac{5}{{16}} = \frac{{5 \times 9}}{{16 \times 9}} = \frac{{45}}{{144}}$
Vậy quy đồng mẫu số hai phân số $\frac{4}{9}$và $\frac{5}{{16}}$ta được $\frac{{64}}{{144}}$và $\frac{{45}}{{144}}$.
Video hướng dẫn giải
Trả lời câu hỏi 7 trang 14 SGK Toán 5 Cánh diều
a)
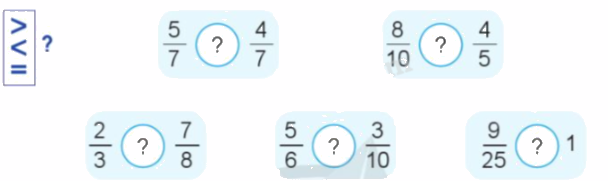
b) Sắp xếp các phân số $\frac{2}{3};\,\frac{6}{7};\,\frac{3}{4}$theo thứ tự từ bé đến lớn.
Phương pháp giải:
- Trong hai phân số có cùng mẫu số: Phân số nào có tử số lớn hơn thì lớn hơn.
- Muốn so sánh hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi quy đồng
Lời giải chi tiết:
a)
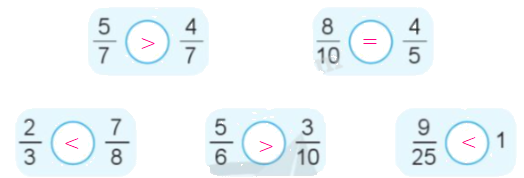
b) Chọn mẫu số chung là 84.
Ta có $\frac{2}{3} = \frac{{2 \times 28}}{{3 \times 28}} = \frac{{56}}{{84}}$
$\frac{6}{7} = \frac{{6 \times 12}}{{7 \times 12}} = \frac{{72}}{{84}}$
$\frac{3}{4} = \frac{{3 \times 21}}{{4 \times 21}} = \frac{{63}}{{84}}$
Vì $\frac{{56}}{{84}} < \frac{{63}}{{84}} < \frac{{72}}{{84}}$nên $\frac{2}{3} < \frac{3}{4} < \frac{6}{7}$.
Vậy các phân số đã cho viết theo thứ tự từ bé đến lớn là $\frac{2}{3};\frac{3}{4};\frac{6}{7}$.
Video hướng dẫn giải
Trả lời câu hỏi 8 trang 14 SGK Toán 5 Cánh diều
Dung và Đức cùng tham gia trò chơi leo dây với các dây có cùng chiều dài. Dung leo được $\frac{5}{8}$sợi dây. Đức leo được $\frac{4}{{10}}$sợi dây.
Theo em:
a) Dung đã leo được sợi dây màu nào? Đức đã leo được sợi dây màu nào?
b) Ai đã leo được đoạn dây dài hơn?
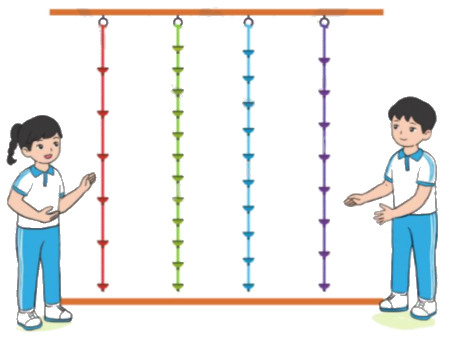
Phương pháp giải:
a) Quan sát hình vẽ và đếm số phần trên mỗi sợi dây.
Sợi dây mỗi bạn leo có mẫu số bằng số phần vừa đếm được.
b) So sánh số phần dây Dung leo được với số phần dây Phúc leo được rồi kết luận
Lời giải chi tiết:
a) Dung đã leo được sợi dây màu cam, Đức đã leo được sợi dây màu xanh dương.
b) Chọn 40 là mẫu số chung. Ta có:
$\frac{5}{8} = \frac{{5 \times 5}}{{8 \times 5}} = \frac{{25}}{{40}}$; $\frac{4}{{10}} = \frac{{4 \times 4}}{{10 \times 4}} = \frac{{16}}{{40}}$
Vì $\frac{{25}}{{40}} > \frac{{16}}{{40}}$ nên $\frac{5}{8} > \frac{4}{{10}}$
Vậy Dung leo được đoạn dây dài hơn Phúc.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 12 SGK Toán 5 Cánh diều
a) Viết phân số chỉ số phần đã tô màu trong mỗi hình rồi đọc (theo mẫu):
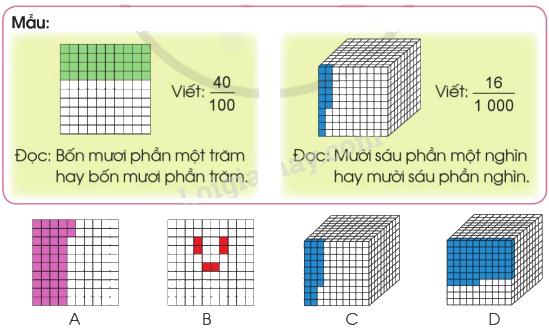
b) Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu):

c) Viết các số tự nhiên sau thành phân số (theo mẫu):

Phương pháp giải:
a) Phân số chỉ phần đã tô màu có tử số chỉ số phần đã tô màu và mẫu số chỉ số phần bằng nhau. Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.
b) Thương của phép chia một số tự nhiên cho một số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.
c) Mọi số tự nhiên đều có thể viết thành phân số có mẫu số là 1.
Lời giải chi tiết:
a)
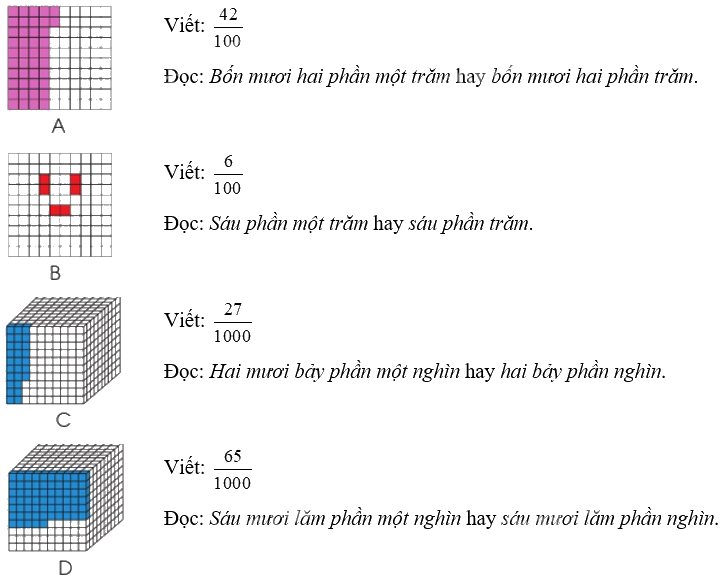
b) 11 : 5 = $\frac{{11}}{5}$ ; $9:100 = \frac{9}{{100}}$ ; $33:30 = \frac{{33}}{{30}}$
c) $301 = \frac{{301}}{1}$ ; $12 = \frac{{12}}{1}$ ; $2025 = \frac{{2025}}{1}$
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 12 SGK Toán 5 Cánh diều
Trò chơi “Ghép thẻ”
a) Ghép các thẻ ghi phân số thích hợp với thẻ hình vẽ có số phần đã tô màu tương ứng:
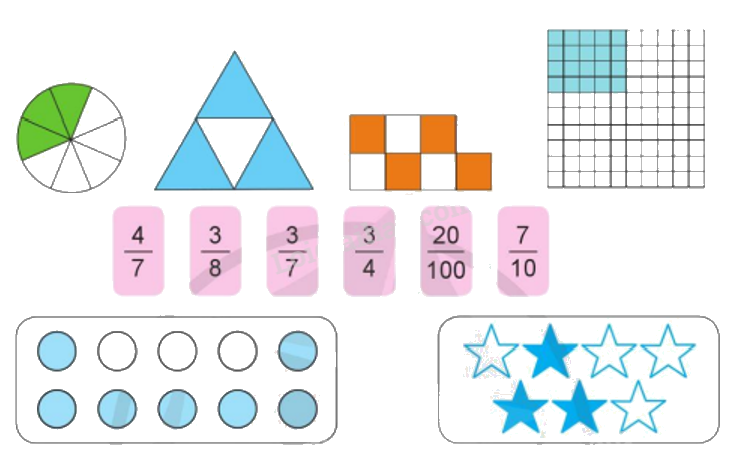
b) Đọc các phân số ở câu a và nêu tử số, mẫu số của mỗi phân số đó.
Phương pháp giải:
a) Phân số chỉ phần đã tô màu có tử số chỉ số phần đã tô màu và mẫu số chỉ số phần bằng nhau. b)
- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số. - Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.
Lời giải chi tiết:
a)
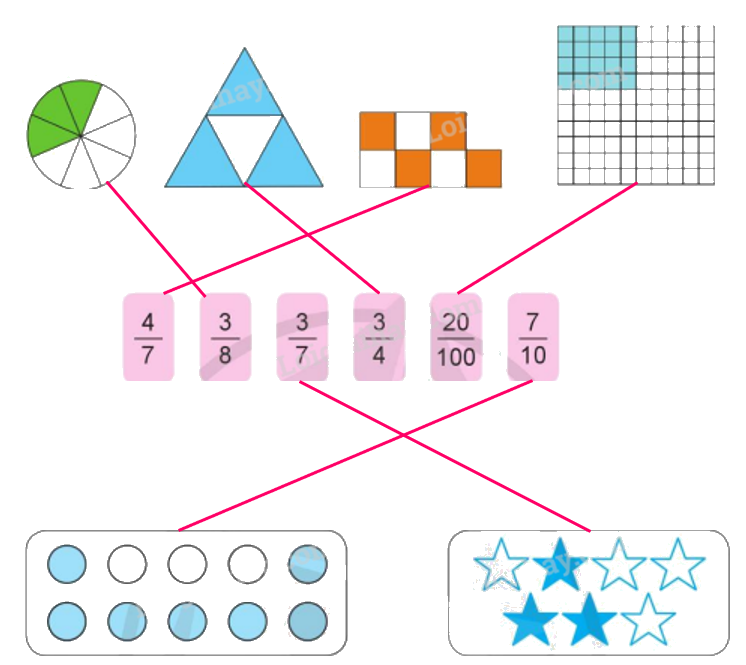
b) $\frac{4}{7}$ đọc là: bốn phần bảy; tử số là 4, mẫu số là 7
$\frac{3}{8}$ đọc là: ba phần tám; tử số là 3, mẫu số là 8
$\frac{3}{7}$ đọc là: ba phần bảy; có tử số là 3, mẫu số là 7
$\frac{3}{4}$ đọc là: ba phần tư; tử số là 3, mẫu số là 4
$\frac{{20}}{{100}}$ đọc là: hai mươi phần một trăm; tử số là 20, mẫu số là 100
$\frac{7}{{10}}$ đọc là: bảy phần mười; tử số là 7, mẫu số là 10
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 12 SGK Toán 5 Cánh diều
Trò chơi “Ghép thẻ”
a) Ghép các thẻ ghi phân số thích hợp với thẻ hình vẽ có số phần đã tô màu tương ứng:
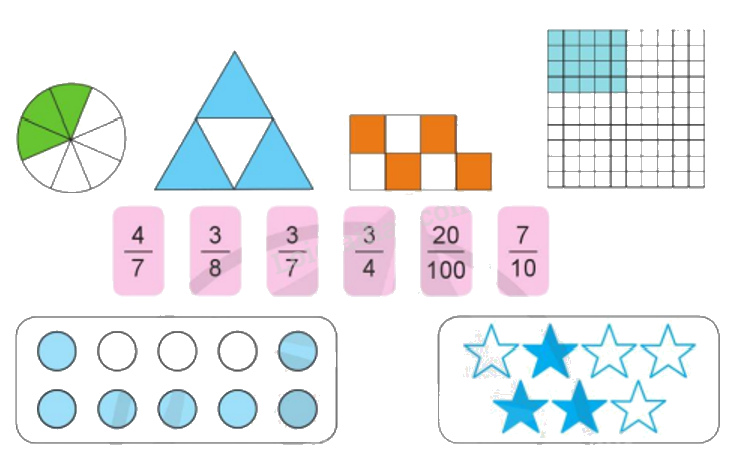
b) Đọc các phân số ở câu a và nêu tử số, mẫu số của mỗi phân số đó.
Phương pháp giải:
a) Phân số chỉ phần đã tô màu có tử số chỉ số phần đã tô màu và mẫu số chỉ số phần bằng nhau. b)
- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số. - Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.
Lời giải chi tiết:
a)
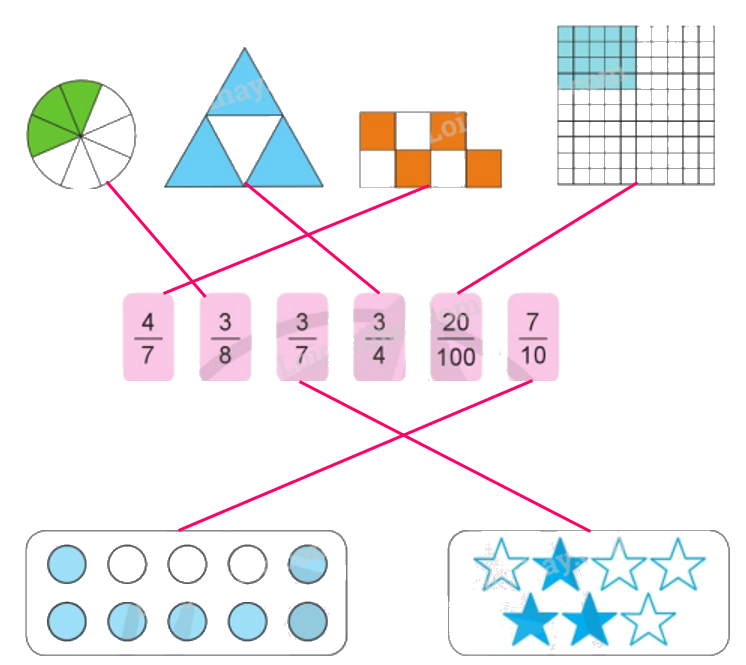
b) $\frac{4}{7}$ đọc là: bốn phần bảy; tử số là 4, mẫu số là 7
$\frac{3}{8}$ đọc là: ba phần tám; tử số là 3, mẫu số là 8
$\frac{3}{7}$ đọc là: ba phần bảy; có tử số là 3, mẫu số là 7
$\frac{3}{4}$ đọc là: ba phần tư; tử số là 3, mẫu số là 4
$\frac{{20}}{{100}}$ đọc là: hai mươi phần một trăm; tử số là 20, mẫu số là 100
$\frac{7}{{10}}$ đọc là: bảy phần mười; tử số là 7, mẫu số là 10
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 12 SGK Toán 5 Cánh diều
a) Viết phân số chỉ số phần đã tô màu trong mỗi hình rồi đọc (theo mẫu):
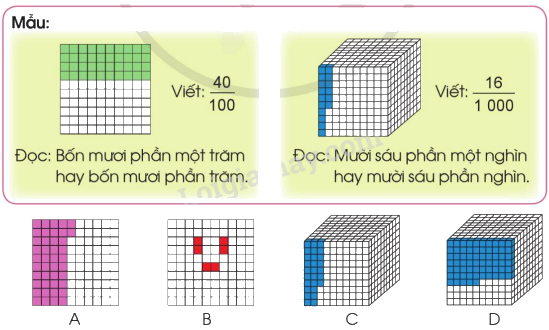
b) Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu):

c) Viết các số tự nhiên sau thành phân số (theo mẫu):

Phương pháp giải:
a) Phân số chỉ phần đã tô màu có tử số chỉ số phần đã tô màu và mẫu số chỉ số phần bằng nhau. Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.
b) Thương của phép chia một số tự nhiên cho một số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.
c) Mọi số tự nhiên đều có thể viết thành phân số có mẫu số là 1.
Lời giải chi tiết:
a)
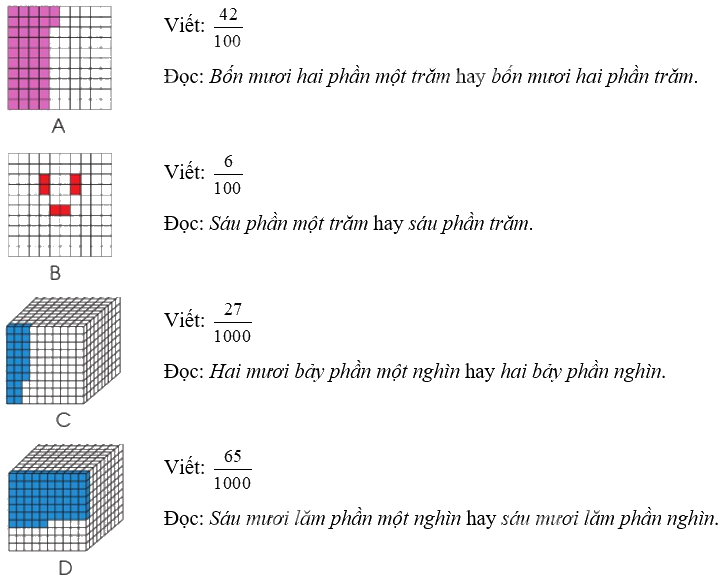
b) 11 : 5 = $\frac{{11}}{5}$ ; $9:100 = \frac{9}{{100}}$ ; $33:30 = \frac{{33}}{{30}}$
c) $301 = \frac{{301}}{1}$ ; $12 = \frac{{12}}{1}$ ; $2025 = \frac{{2025}}{1}$
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 13 SGK Toán 5 Cánh diều
a) Nêu hai phân số bằng mỗi phân số sau: $\frac{5}{4};\,\frac{9}{{12}}$.
b) Rút gọn các phân số sau: $\frac{{24}}{{32}};\,\,\frac{{14}}{{35}};\,\,\frac{{30}}{{25}};\,\,\frac{{63}}{{36}}$
Phương pháp giải:
a) Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
b) Rút gọn phân số:
• Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
• Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
a) \(\frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}}\) ; \(\frac{5}{4} = \frac{{5 \times 5}}{{4 \times 5}} = \frac{{25}}{{20}}\)
Hai phân số bằng phân số $\frac{5}{4}$là $\frac{{15}}{{12}}$và $\frac{{25}}{{20}}$
\(\frac{9}{{12}} = \frac{{9:3}}{{12:3}} = \frac{3}{4}\) ; \(\frac{9}{{12}} = \frac{{9 \times 2}}{{12 \times 2}} = \frac{{18}}{{24}}\)
Hai phân số bằng phân số $\frac{9}{{12}}$là $\frac{3}{4}$và $\frac{{18}}{{24}}$
b) $\frac{{24}}{{32}} = \frac{{24:8}}{{32:8}} = \frac{3}{4}$
$\frac{{14}}{{35}} = \frac{{14:7}}{{35:7}} = \frac{2}{5}$
$\frac{{30}}{{25}} = \frac{{30:5}}{{25:5}} = \frac{6}{5}$
$\frac{{63}}{{36}} = \frac{{63:9}}{{36:9}} = \frac{7}{4}$
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 13 SGK Toán 5 Cánh diều
Quy đồng mẫu số hai phân số:

Phương pháp giải:
- Tìm mẫu số chung- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
a) $\frac{4}{7} = \frac{{4 \times 2}}{{7 \times 2}} = \frac{8}{{14}}$; giữ nguyên phân số $\frac{3}{{14}}$.
Vậy quy đồng mẫu số hai phân số $\frac{3}{{14}}$và $\frac{4}{7}$ta được $\frac{3}{{14}}$và $\frac{8}{{14}}$.
b) $\frac{2}{3} = \frac{{2 \times 2}}{{3 \times 2}} = \frac{4}{6}$; giữ nguyên phân số $\frac{5}{6}$.
Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$và $\frac{5}{6}$ta được $\frac{4}{6}$và $\frac{5}{6}$.
Video hướng dẫn giải
Trả lời câu hỏi 5 trang 13 SGK Toán 5 Cánh diều
a) Đọc ví dụ sau rồi nói cho bạn nghe cách thực hiện:
Ví dụ: Quy đồng mẫu số hai phân số $\frac{2}{3}$và $\frac{5}{4}$
Vì 3 x 4 = 12 nên ta chọn 12 làm mẫu số chung.
Ta có: $\frac{2}{3} = \frac{{2 \times 4}}{{3 \times 4}} = \frac{8}{{12}}$ và $\frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}}$
Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$và $\frac{5}{4}$ta được $\frac{8}{{12}}$và $\frac{{15}}{{12}}$
b) Quy đồng mẫu số hai phân số:
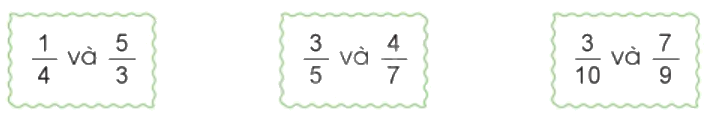
Phương pháp giải:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Lời giải chi tiết:
a) Cách quy đồng mẫu số:
- Chọn mẫu số chung
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
b)
$\frac{1}{4}$và $\frac{5}{3}$
Vì 4 x 3 = 12 nên ta chọn 12 làm mẫu số chung.
Ta có: \(\frac{1}{4} = \frac{{1 \times 3}}{{4 \times 3}} = \frac{3}{{12}}\) và $\frac{5}{3} = \frac{{5 \times 4}}{{3 \times 4}} = \frac{{20}}{{12}}$
Vậy quy đồng mẫu số hai phân số $\frac{1}{4}$và $\frac{5}{3}$ta được $\frac{3}{{12}}$và $\frac{{20}}{{12}}$.
$\frac{3}{5}$và $\frac{4}{7}$
Vì 5 x 7 = 35 nên ta chọn 35 làm mẫu số chung.
Ta có: \(\frac{3}{5} = \frac{{3 \times 7}}{{5 \times 7}} = \frac{{21}}{{35}}\) và $\frac{4}{7} = \frac{{4 \times 5}}{{7 \times 5}} = \frac{{20}}{{35}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{5}$và $\frac{4}{7}$ta được $\frac{{21}}{{35}}$và $\frac{{20}}{{35}}$.
$\frac{3}{{10}}$và $\frac{7}{9}$
Vì 10 x 9 = 90 nên ta chọn 90 làm mẫu số chung.
Ta có: \(\frac{3}{{10}} = \frac{{3 \times 9}}{{10 \times 9}} = \frac{{27}}{{90}}\) và $\frac{7}{9} = \frac{{7 \times 10}}{{9 \times 10}} = \frac{{70}}{{90}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{{10}}$và $\frac{7}{9}$ta được $\frac{{27}}{{90}}$và $\frac{{70}}{{90}}$
Video hướng dẫn giải
Trả lời câu hỏi 6 trang 14 SGK Toán 5 Cánh diều
Quy đồng mẫu số hai phân số:

Phương pháp giải:
- Tìm mẫu số chung
- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
+) $\frac{3}{4}$và $\frac{1}{6}$
Chọn 12 làm mẫu số chung.
Ta có: $\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$ và $\frac{1}{6} = \frac{{1 \times 2}}{{6 \times 2}} = \frac{2}{{12}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{4}$và $\frac{1}{6}$ ta được $\frac{9}{{12}}$và $\frac{2}{{12}}$.
+) $\frac{7}{{10}}$ và $\frac{5}{8}$
Chọn 40 làm mẫu số chung.
Ta có: $\frac{7}{{10}} = \frac{{7 \times 4}}{{10 \times 4}} = \frac{{28}}{{40}}$ và $\frac{5}{8} = \frac{{5 \times 5}}{{8 \times 5}} = \frac{{25}}{{40}}$
Vậy quy đồng mẫu số hai phân số $\frac{7}{{10}}$và $\frac{5}{8}$ ta được $\frac{{28}}{{40}}$và $\frac{{25}}{{40}}$.
+) $\frac{4}{9}$ và $\frac{5}{{16}}$
Chọn 144 làm mẫu số chung.
Ta có: \(\frac{4}{9} = \frac{{4 \times 16}}{{9 \times 16}} = \frac{{64}}{{144}}\) và $\frac{5}{{16}} = \frac{{5 \times 9}}{{16 \times 9}} = \frac{{45}}{{144}}$
Vậy quy đồng mẫu số hai phân số $\frac{4}{9}$và $\frac{5}{{16}}$ta được $\frac{{64}}{{144}}$và $\frac{{45}}{{144}}$.
Video hướng dẫn giải
Trả lời câu hỏi 7 trang 14 SGK Toán 5 Cánh diều
a)
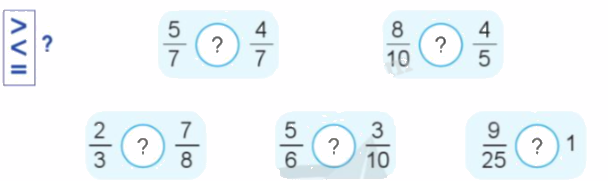
b) Sắp xếp các phân số $\frac{2}{3};\,\frac{6}{7};\,\frac{3}{4}$theo thứ tự từ bé đến lớn.
Phương pháp giải:
- Trong hai phân số có cùng mẫu số: Phân số nào có tử số lớn hơn thì lớn hơn.
- Muốn so sánh hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi quy đồng
Lời giải chi tiết:
a)
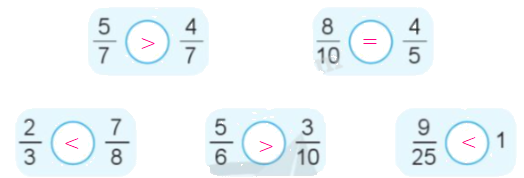
b) Chọn mẫu số chung là 84.
Ta có $\frac{2}{3} = \frac{{2 \times 28}}{{3 \times 28}} = \frac{{56}}{{84}}$
$\frac{6}{7} = \frac{{6 \times 12}}{{7 \times 12}} = \frac{{72}}{{84}}$
$\frac{3}{4} = \frac{{3 \times 21}}{{4 \times 21}} = \frac{{63}}{{84}}$
Vì $\frac{{56}}{{84}} < \frac{{63}}{{84}} < \frac{{72}}{{84}}$nên $\frac{2}{3} < \frac{3}{4} < \frac{6}{7}$.
Vậy các phân số đã cho viết theo thứ tự từ bé đến lớn là $\frac{2}{3};\frac{3}{4};\frac{6}{7}$.
Video hướng dẫn giải
Trả lời câu hỏi 8 trang 14 SGK Toán 5 Cánh diều
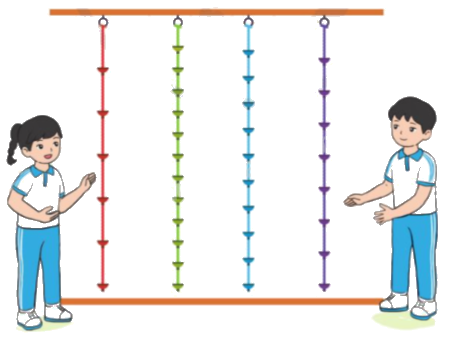
Dung và Đức cùng tham gia trò chơi leo dây với các dây có cùng chiều dài. Dung leo được $\frac{5}{8}$sợi dây. Đức leo được $\frac{4}{{10}}$sợi dây.
Theo em:
a) Dung đã leo được sợi dây màu nào? Đức đã leo được sợi dây màu nào?
b) Ai đã leo được đoạn dây dài hơn?
Phương pháp giải:
a) Quan sát hình vẽ và đếm số phần trên mỗi sợi dây.
Sợi dây mỗi bạn leo có mẫu số bằng số phần vừa đếm được.
b) So sánh số phần dây Dung leo được với số phần dây Phúc leo được rồi kết luận
Lời giải chi tiết:
a) Dung đã leo được sợi dây màu cam, Đức đã leo được sợi dây màu xanh dương.
b) Chọn 40 là mẫu số chung. Ta có:
$\frac{5}{8} = \frac{{5 \times 5}}{{8 \times 5}} = \frac{{25}}{{40}}$; $\frac{4}{{10}} = \frac{{4 \times 4}}{{10 \times 4}} = \frac{{16}}{{40}}$
Vì $\frac{{25}}{{40}} > \frac{{16}}{{40}}$ nên $\frac{5}{8} > \frac{4}{{10}}$
Vậy Dung leo được đoạn dây dài hơn Phúc.
Bài 4 trong chương trình Toán lớp 5 sách Cánh Diều tập trung vào việc ôn tập và bổ sung kiến thức về phân số. Đây là một chủ đề quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn. Bài học này giúp học sinh hệ thống lại các khái niệm cơ bản về phân số, các phép toán với phân số, và ứng dụng của phân số trong thực tế.
Phân số là một biểu thức toán học dùng để biểu diễn một phần của một đơn vị hoặc một tập hợp. Một phân số có hai phần: tử số (phần được lấy ra) và mẫu số (phần chung). Ví dụ, phân số 2/3 có tử số là 2 và mẫu số là 3.
Các phép toán cơ bản với phân số bao gồm:
Dưới đây là một số bài tập vận dụng để giúp các em học sinh hiểu rõ hơn về bài học:
Chúng tôi sẽ cung cấp lời giải chi tiết cho từng bài tập trong SGK Cánh Diều Toán lớp 5 Bài 4. Các em học sinh có thể tham khảo để hiểu rõ cách giải và tự luyện tập.
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Giải thích chi tiết bài 1) |
| Bài 2 | (Giải thích chi tiết bài 2) |
| Bài 3 | (Giải thích chi tiết bài 3) |
Để học tốt về phân số, các em học sinh cần:
Hy vọng rằng bài viết này sẽ giúp các em học sinh hiểu rõ hơn về Toán lớp 5 Bài 4: Ôn tập và bổ sung về phân số - SGK Cánh Diều và đạt kết quả tốt trong học tập.