Bài 61 Toán lớp 5 thuộc chương trình học Toán 5 Cánh Diều, là bài luyện tập tổng hợp các kiến thức đã học về các phép tính với số thập phân, đo lường thời gian, diện tích hình chữ nhật và hình vuông. Bài học này giúp học sinh củng cố kỹ năng giải toán và áp dụng kiến thức vào thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Bài 61, giúp các em học sinh tự tin chinh phục môn Toán.
a) Quan sát hình vẽ, nêu số đo thích hợp: b) Tính diện tích xung quanh và diện tích toàn phần của mỗi hình ở câu a. Số? a) Một ngăn kéo làm bằng gỗ có dạng hình hộp chữ nhật với kích thước như hình bên. Tính diện tích phần gỗ của ngăn kéo đó. Quan sát các hình sau và cho biết mảnh bìa nào có thể gấp thành hình lập phương, hình hộp chữ nhật. Một công ty sản xuất hai loại hộp bằng bìa cứng có dạng hình hộp chữ nhật với kích thước như bảng dưới đây:
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 35 SGK Toán 5 Cánh diều
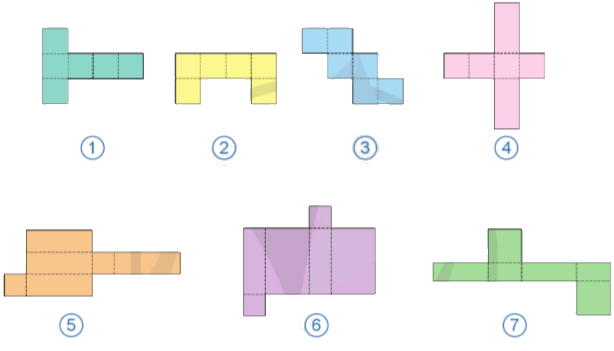
Quan sát các hình sau và cho biết mảnh bìa nào có thể gấp thành hình lập phương, hình hộp chữ nhật.
Phương pháp giải:
Quan sát hình và trả lời.
Lời giải chi tiết:
- Mảnh bìa 1 và 3 có thể gấp thành hình lập phương.
- Mảnh bìa 5 có thể gấp thành hình hộp chữ nhật.
Video hướng dẫn giải
Trả lời câu hỏi 5 trang 35 SGK Toán 5 Cánh diều
Một công ty sản xuất hai loại hộp bằng bìa cứng có dạng hình hộp chữ nhật với kích thước như bảng dưới đây:
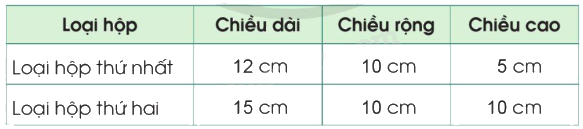
a) Tính diện tích bìa cần dùng để làm một chiếc hộp mỗi loại.
b) Ước lượng số tiền mua bìa để sản xuất một chiếc hộp mỗi loại, biết rằng cứ 1 m2 bìa thì làm được khoảng 20 chiếc hộp loại thứ nhất và làm được khoảng 12 chiếc hộp loại thứ hai. Loại bìa được sử dụng có giá là 24000 đồng 1 m2.
Phương pháp giải:
a) Diện tích bìa cần dùng để làm một chiếc hộp mỗi loại = diện tích toàn phần của mỗi chiếc hộp
b) Tính giá tiền mua bìa để sản xuất một chiếc hộp mỗi loại = số tiền 1 m2 bìa : số hộp
Lời giải chi tiết:
a) Diện tích xung quanh của loại hộp thứ nhất là:
$\left( {12 + 10} \right) \times 2 \times 5 = 220$ (cm2)
Diện tích mặt đáy của loại hộp thứ nhất là:
$12 \times 10 = 120$ (cm2)
Diên tích bìa cần dùng để làm một chiếc hộp loại thứ nhất là:
$220 + 120 \times 2 = 460$ (cm2)
Diện tích xung quanh của loại hộp thứ hai là:
$\left( {15 + 10} \right) \times 2 \times 10 = 500$(cm2)
Diện tích mặt đáy của loại hộp thứ hai là:
$15 \times 10 = 150$ (cm2)
Diên tích bìa cần dùng để làm một chiếc hộp loại thứ hai là:
$500 + 150 \times 2 = 800$ (cm2)
b)
Số tiền mua bìa để sản xuất một chiếc hộp loại thứ nhất là:
24 000 : 20 = 1 200 (đồng)
Số tiền mua bìa để sản xuất một chiếc hộp loại thứ hai là:
24 000 : 12 = 2 000 (đồng)
Đáp số: a) loại hộp thứ nhất: 460 cm2; loại hộp thứ hai: 800 cm2.
b) loại hộp thứ nhất: 1200 đồng; loại hộp thứ hai: 2000 đồng
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 34 SGK Toán 5 Cánh diều
a) Một ngăn kéo làm bằng gỗ có dạng hình hộp chữ nhật với kích thước như hình bên. Tính diện tích phần gỗ của ngăn kéo đó.
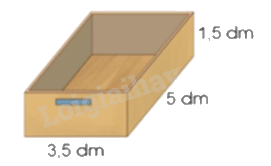
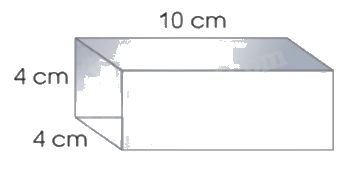
b) Một đoạn ống thép có có dạng hình hộp chữ nhật với kích thước như hình bên. Tính diện tích thép đủ để làm 30 đoạn ống như thế.
Phương pháp giải:
a) Ngăn kéo không có mặt trên nên diện tích phần gỗ của ngăn kéo là tổng của diện tích xung quanh của ngăn kéo và diện tích đáy của ngăn kéo.
b) Đoạn ống thép không có 2 đầu và rỗng ở giữa nên diện tích ống thép là diện tích xung quanh của ống thép với chiều cao là 10 cm. Hình ảnh ống thép lúc này:
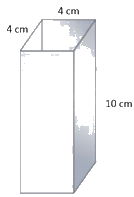
- Tính diện tích thép đủ để làm 30 đoạn ống = diện tích xung quanh của ống thép x 30
Lời giải chi tiết:
a) Diện tích xung quanh của ngăn kéo là:
$\left( {3,5 + 5} \right) \times 2 \times 1,5 = 25,5$(dm2)
Diện tích đáy của ngăn kéo là:
$3,5 \times 5 = 17,5$(dm2)
Diện tích phần gỗ của ngăn kéo đó là:
25,5 + 17,5 = 43 (dm2)
b) Diện tích xung quanh của ống thép là:
4 x 4 x 10 = 160 (cm2)
Diện tích thép đủ để làm 30 đoạn ống là:
160 x 30 = 4800 (cm2)
Đáp số: a) 43 dm2;
b) 4800 cm2.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 34 SGK Toán 5 Cánh diều
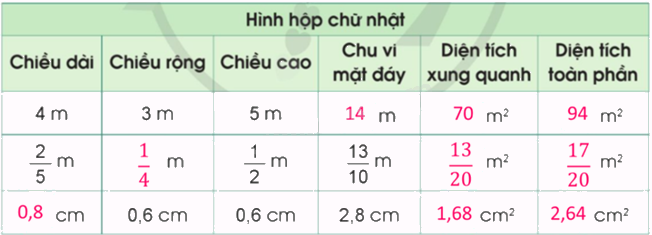
Số?
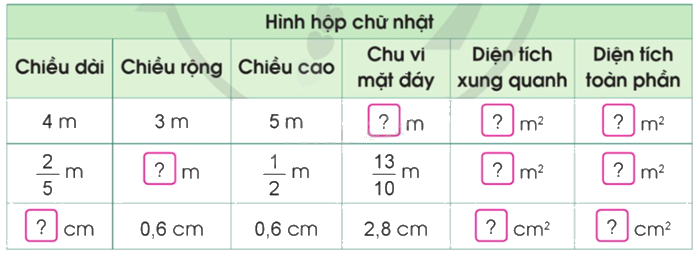
Phương pháp giải:
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Lời giải chi tiết:
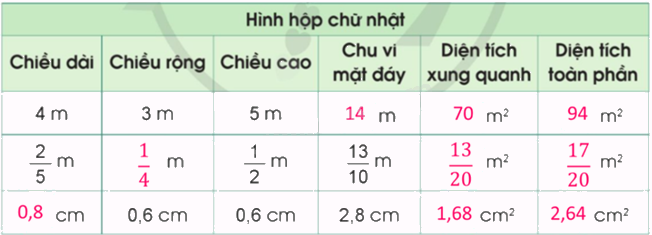
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 34 SGK Toán 5 Cánh diều
Đề bài
a) Quan sát hình vẽ, nêu số đo thích hợp:
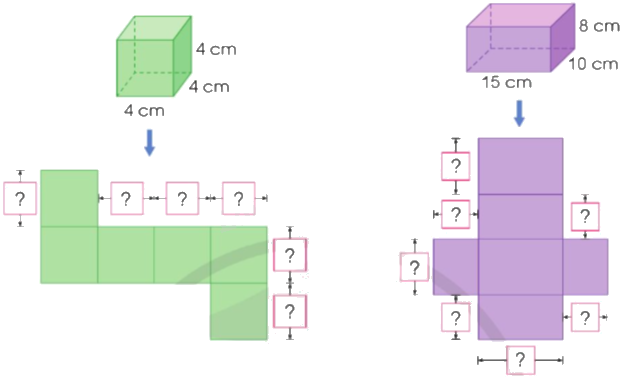
b) Tính diện tích xung quanh và diện tích toàn phần của mỗi hình ở câu a.
Phương pháp giải:
a) Quan sát hình và dựa vào tính chất của hình hộp chữ nhật, hình lập phương.
b)
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 4.
- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân với 6.
Lời giải chi tiết:
a)
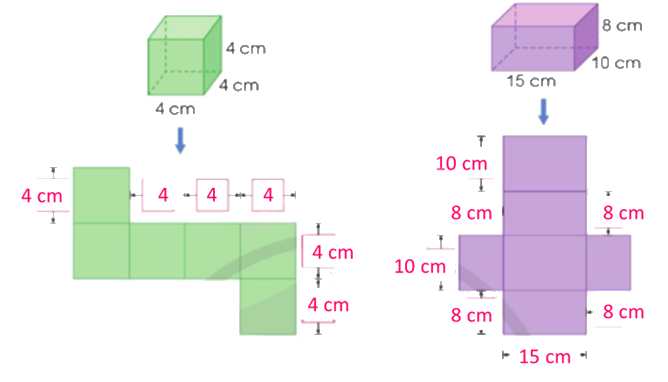
b)
+ Diện tích xung quanh của hình lập phương đó là:
$4 \times 4 \times 4 = 64$ (cm2)
Diện tích toàn phần của hình lập phương đó là:
$4 \times 4 \times 6 = 96$(cm2)
+ Diện tích xung quanh của hình hộp chữ nhật đó là:
$\left( {10 + 15} \right) \times 2 \times 8 = 400$ (cm2)
Diện tích một mặt đáy của hình hộp chữ nhật đó là:
$15 \times 10 = 150$(cm2)
Diện tích toàn phần của hình hộp chữ nhật đó là:
$400 + 150 \times 2 = 700$(cm2)
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 34 SGK Toán 5 Cánh diều
Đề bài
a) Quan sát hình vẽ, nêu số đo thích hợp:
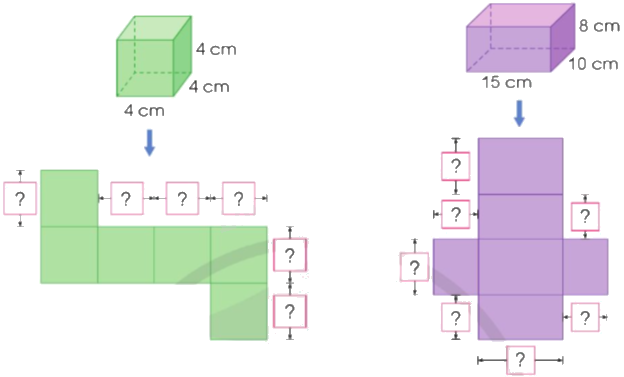
b) Tính diện tích xung quanh và diện tích toàn phần của mỗi hình ở câu a.
Phương pháp giải:
a) Quan sát hình và dựa vào tính chất của hình hộp chữ nhật, hình lập phương.
b)
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 4.
- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân với 6.
Lời giải chi tiết:
a)
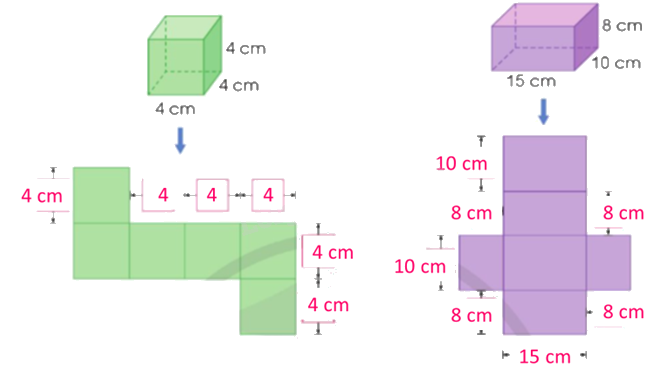
b)
+ Diện tích xung quanh của hình lập phương đó là:
$4 \times 4 \times 4 = 64$ (cm2)
Diện tích toàn phần của hình lập phương đó là:
$4 \times 4 \times 6 = 96$(cm2)
+ Diện tích xung quanh của hình hộp chữ nhật đó là:
$\left( {10 + 15} \right) \times 2 \times 8 = 400$ (cm2)
Diện tích một mặt đáy của hình hộp chữ nhật đó là:
$15 \times 10 = 150$(cm2)
Diện tích toàn phần của hình hộp chữ nhật đó là:
$400 + 150 \times 2 = 700$(cm2)
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 34 SGK Toán 5 Cánh diều
Số?
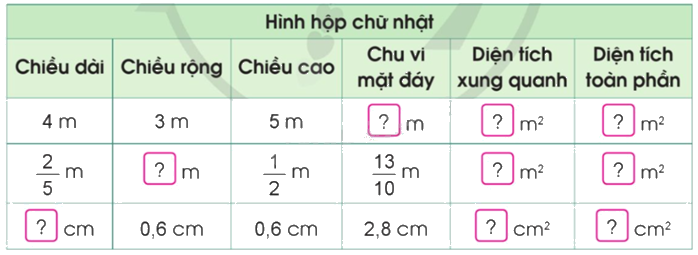
Phương pháp giải:
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Lời giải chi tiết:
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 34 SGK Toán 5 Cánh diều
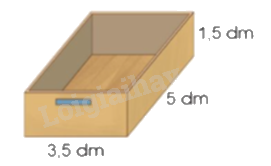
a) Một ngăn kéo làm bằng gỗ có dạng hình hộp chữ nhật với kích thước như hình bên. Tính diện tích phần gỗ của ngăn kéo đó.
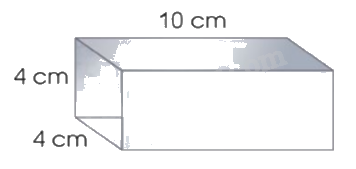
b) Một đoạn ống thép có có dạng hình hộp chữ nhật với kích thước như hình bên. Tính diện tích thép đủ để làm 30 đoạn ống như thế.
Phương pháp giải:
a) Ngăn kéo không có mặt trên nên diện tích phần gỗ của ngăn kéo là tổng của diện tích xung quanh của ngăn kéo và diện tích đáy của ngăn kéo.
b) Đoạn ống thép không có 2 đầu và rỗng ở giữa nên diện tích ống thép là diện tích xung quanh của ống thép với chiều cao là 10 cm. Hình ảnh ống thép lúc này:
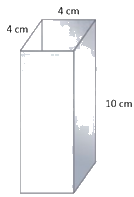
- Tính diện tích thép đủ để làm 30 đoạn ống = diện tích xung quanh của ống thép x 30
Lời giải chi tiết:
a) Diện tích xung quanh của ngăn kéo là:
$\left( {3,5 + 5} \right) \times 2 \times 1,5 = 25,5$(dm2)
Diện tích đáy của ngăn kéo là:
$3,5 \times 5 = 17,5$(dm2)
Diện tích phần gỗ của ngăn kéo đó là:
25,5 + 17,5 = 43 (dm2)
b) Diện tích xung quanh của ống thép là:
4 x 4 x 10 = 160 (cm2)
Diện tích thép đủ để làm 30 đoạn ống là:
160 x 30 = 4800 (cm2)
Đáp số: a) 43 dm2;
b) 4800 cm2.
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 35 SGK Toán 5 Cánh diều
Quan sát các hình sau và cho biết mảnh bìa nào có thể gấp thành hình lập phương, hình hộp chữ nhật.
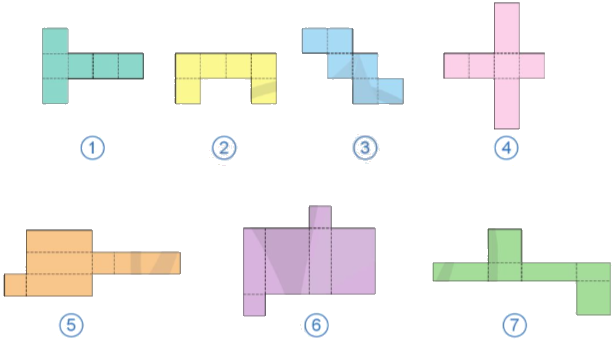
Phương pháp giải:
Quan sát hình và trả lời.
Lời giải chi tiết:
- Mảnh bìa 1 và 3 có thể gấp thành hình lập phương.
- Mảnh bìa 5 có thể gấp thành hình hộp chữ nhật.
Video hướng dẫn giải
Trả lời câu hỏi 5 trang 35 SGK Toán 5 Cánh diều
Một công ty sản xuất hai loại hộp bằng bìa cứng có dạng hình hộp chữ nhật với kích thước như bảng dưới đây:
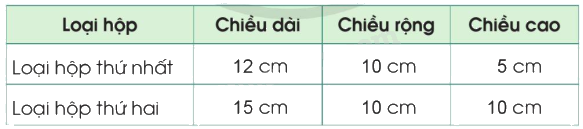
a) Tính diện tích bìa cần dùng để làm một chiếc hộp mỗi loại.
b) Ước lượng số tiền mua bìa để sản xuất một chiếc hộp mỗi loại, biết rằng cứ 1 m2 bìa thì làm được khoảng 20 chiếc hộp loại thứ nhất và làm được khoảng 12 chiếc hộp loại thứ hai. Loại bìa được sử dụng có giá là 24000 đồng 1 m2.
Phương pháp giải:
a) Diện tích bìa cần dùng để làm một chiếc hộp mỗi loại = diện tích toàn phần của mỗi chiếc hộp
b) Tính giá tiền mua bìa để sản xuất một chiếc hộp mỗi loại = số tiền 1 m2 bìa : số hộp
Lời giải chi tiết:
a) Diện tích xung quanh của loại hộp thứ nhất là:
$\left( {12 + 10} \right) \times 2 \times 5 = 220$ (cm2)
Diện tích mặt đáy của loại hộp thứ nhất là:
$12 \times 10 = 120$ (cm2)
Diên tích bìa cần dùng để làm một chiếc hộp loại thứ nhất là:
$220 + 120 \times 2 = 460$ (cm2)
Diện tích xung quanh của loại hộp thứ hai là:
$\left( {15 + 10} \right) \times 2 \times 10 = 500$(cm2)
Diện tích mặt đáy của loại hộp thứ hai là:
$15 \times 10 = 150$ (cm2)
Diên tích bìa cần dùng để làm một chiếc hộp loại thứ hai là:
$500 + 150 \times 2 = 800$ (cm2)
b)
Số tiền mua bìa để sản xuất một chiếc hộp loại thứ nhất là:
24 000 : 20 = 1 200 (đồng)
Số tiền mua bìa để sản xuất một chiếc hộp loại thứ hai là:
24 000 : 12 = 2 000 (đồng)
Đáp số: a) loại hộp thứ nhất: 460 cm2; loại hộp thứ hai: 800 cm2.
b) loại hộp thứ nhất: 1200 đồng; loại hộp thứ hai: 2000 đồng
Bài 61 Toán lớp 5 Cánh Diều là một bài tập luyện tập quan trọng, giúp học sinh ôn lại và củng cố kiến thức đã học trong chương trình Toán 5. Bài tập bao gồm nhiều dạng bài khác nhau, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức về số thập phân, các phép tính với số thập phân, đo lường thời gian, diện tích hình chữ nhật và hình vuông.
Bài 61 tập trung vào việc giải các bài toán thực tế liên quan đến các kiến thức đã học. Cụ thể, bài tập thường gặp các dạng sau:
Để giúp học sinh giải quyết các bài tập trong Bài 61 một cách hiệu quả, chúng tôi xin đưa ra hướng dẫn giải chi tiết cho từng bài tập:
Bài 1 yêu cầu học sinh tính nhẩm nhanh các phép tính đơn giản với số thập phân. Để tính nhẩm nhanh, học sinh có thể sử dụng các kỹ năng như:
Bài 2 yêu cầu học sinh thực hiện các phép tính với số thập phân. Để thực hiện các phép tính này, học sinh cần nắm vững các quy tắc sau:
Để tính diện tích hình chữ nhật, học sinh cần sử dụng công thức: Diện tích = Chiều dài x Chiều rộng. Trong bài này, ta có:
Diện tích = 5,4m x 3,5m = 18,9 m2
Để học tốt Toán lớp 5 Bài 61, học sinh cần:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt Toán lớp 5:
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải quyết các bài tập trong Bài 61 Toán lớp 5 Cánh Diều và đạt kết quả tốt trong môn học.