Bài học Toán lớp 5 Bài 55: Chu vi hình tròn - SGK Cánh Diều giúp các em học sinh nắm vững kiến thức về khái niệm chu vi hình tròn, công thức tính chu vi và ứng dụng vào giải các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cùng với các bài tập luyện tập đa dạng để hỗ trợ các em học sinh ôn tập và củng cố kiến thức một cách hiệu quả.
Tính chu vi của mỗi hình tròn sau: Hoàn thành bảng sau: a) Đường kính của một bánh xe ô tô là 0,6 m. Tính chu vi bánh xe đó. b) Bán kính của một vòng đu quay là 10 m. Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì bạn đã di chuyển được bao nhiêu mét? Hai con kiến bò một vòng xung quanh một hình vuông và một hình tròn như hình vẽ dưới đây. Theo em, con kiến nào đã bò được quãng đường dài hơn? Tại sao? Thực hành: Tìm trong sân trường một cây to, đo độ dài một vòng quanh thân cây rồi ước lư
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 18 SGK Toán 5 Cánh diều
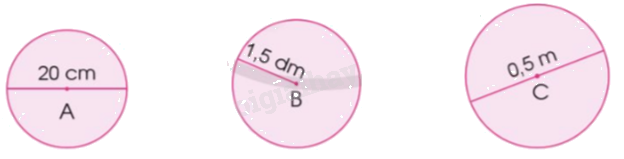
Tính chu vi của mỗi hình tròn sau:
Phương pháp giải:
Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
Muốn tính chu vi của hình tròn, ta lấy 2 lần bán kính nhân với số 3,14.
Lời giải chi tiết:
Chu vi hình tròn tâm A là:
20 x 3,14 = 62,8 (cm)
Chu vi hình tròn tâm B là:
1,5 x 2 x 3,14 = 9,42 (dm)
Chu vi hình tròn tâm C là:
0,5 x 3,14 = 1,57 (m)
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 19 SGK Toán 5 Cánh diều
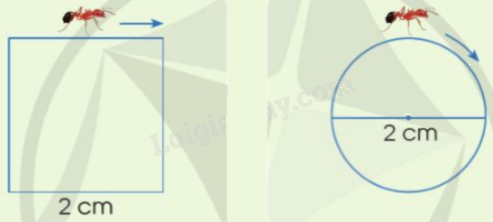
Hai con kiến bò một vòng xung quanh một hình vuông và một hình tròn như hình vẽ dưới đây. Theo em, con kiến nào đã bò được quãng đường dài hơn? Tại sao?
Phương pháp giải:
Quãng đường 2 con kiến bò đường bằng chu vi hình vuông và chu vi hình tròn.
Lời giải chi tiết:
Quãng đường con kiến bò một vòng xung quanh một hình vuông là:
2 x 4 = 8 (cm)
Quãng đường con kiến bò một vòng xung quanh một hình tròn là:
2 x 3,14 = 6,28 (cm)
Vì 8 > 6,28 nên con kiến bò một vòng xung quanh hình vuông đã bò được quãng đường dài hơn.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 18 SGK Toán 5 Cánh diều
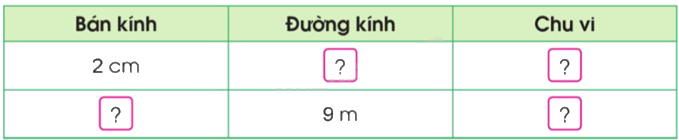
Hoàn thành bảng sau:
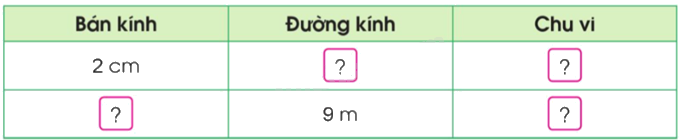
Phương pháp giải:
Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
Đường kính dài gấp 2 lần bán kính.
Lời giải chi tiết:
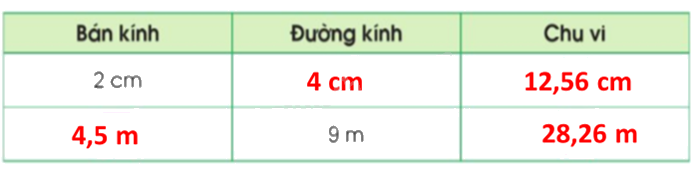
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 19 SGK Toán 5 Cánh diều
a) Đường kính của một bánh xe ô tô là 0,6 m. Tính chu vi bánh xe đó.
b) Bán kính của một vòng đu quay là 10 m. Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì bạn đã di chuyển được bao nhiêu mét?

(Nguồn: https://shutterstock.com)
Phương pháp giải:
a) Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
b) Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì quãng đường đi được chính là chu vi hình tròn.
Lời giải chi tiết:
a) Chu vi bánh xe đó là:
0,6 x 3,14 = 1,884 (m)
b) Chu vi của một vòng đu quay là:
10 x 2 x 3,14 = 62,8 (m)
Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì quãng đường đi được chính là chu vi hình tròn.
Vậy bạn đã di chuyển được 62,8 m.
Video hướng dẫn giải
Trả lời câu hỏi 5 trang 19 SGK Toán 5 Cánh diều
Thực hành: Tìm trong sân trường một cây to, đo độ dài một vòng quanh thân cây rồi ước lượng độ dài đường kính của thân cây.

Phương pháp giải:
- Độ dài một vòng quanh thân cây chính là chu vi của thân cây.
- Tính đường kính của thân cây = độ dài một vòng quanh thân cây : 3,14
Lời giải chi tiết:
Ví dụ: Độ dài một vòng quanh thân cây là 150 cm.
Vậy đường kính của thân cây là:
150 : 3,14 = 47,77 (cm)
Làm tròn đến số tự nhiên ta được 48 cm.
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 18 SGK Toán 5 Cánh diều
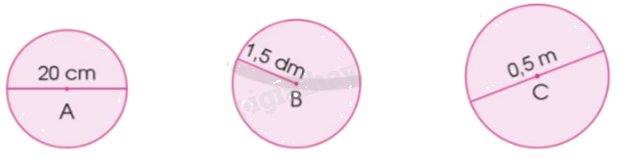
Tính chu vi của mỗi hình tròn sau:
Phương pháp giải:
Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
Muốn tính chu vi của hình tròn, ta lấy 2 lần bán kính nhân với số 3,14.
Lời giải chi tiết:
Chu vi hình tròn tâm A là:
20 x 3,14 = 62,8 (cm)
Chu vi hình tròn tâm B là:
1,5 x 2 x 3,14 = 9,42 (dm)
Chu vi hình tròn tâm C là:
0,5 x 3,14 = 1,57 (m)
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 18 SGK Toán 5 Cánh diều
Hoàn thành bảng sau:
Phương pháp giải:
Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
Đường kính dài gấp 2 lần bán kính.
Lời giải chi tiết:
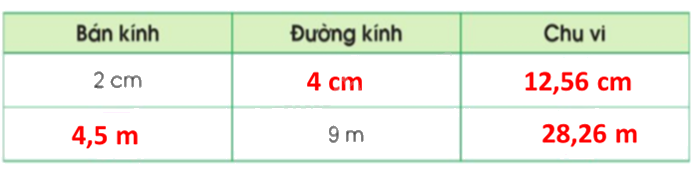
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 19 SGK Toán 5 Cánh diều
a) Đường kính của một bánh xe ô tô là 0,6 m. Tính chu vi bánh xe đó.
b) Bán kính của một vòng đu quay là 10 m. Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì bạn đã di chuyển được bao nhiêu mét?

(Nguồn: https://shutterstock.com)
Phương pháp giải:
a) Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
b) Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì quãng đường đi được chính là chu vi hình tròn.
Lời giải chi tiết:
a) Chu vi bánh xe đó là:
0,6 x 3,14 = 1,884 (m)
b) Chu vi của một vòng đu quay là:
10 x 2 x 3,14 = 62,8 (m)
Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì quãng đường đi được chính là chu vi hình tròn.
Vậy bạn đã di chuyển được 62,8 m.
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 19 SGK Toán 5 Cánh diều
Hai con kiến bò một vòng xung quanh một hình vuông và một hình tròn như hình vẽ dưới đây. Theo em, con kiến nào đã bò được quãng đường dài hơn? Tại sao?
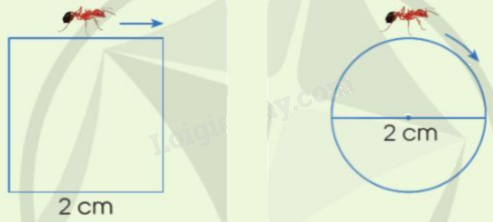
Phương pháp giải:
Quãng đường 2 con kiến bò đường bằng chu vi hình vuông và chu vi hình tròn.
Lời giải chi tiết:
Quãng đường con kiến bò một vòng xung quanh một hình vuông là:
2 x 4 = 8 (cm)
Quãng đường con kiến bò một vòng xung quanh một hình tròn là:
2 x 3,14 = 6,28 (cm)
Vì 8 > 6,28 nên con kiến bò một vòng xung quanh hình vuông đã bò được quãng đường dài hơn.
Video hướng dẫn giải
Trả lời câu hỏi 5 trang 19 SGK Toán 5 Cánh diều
Thực hành: Tìm trong sân trường một cây to, đo độ dài một vòng quanh thân cây rồi ước lượng độ dài đường kính của thân cây.

Phương pháp giải:
- Độ dài một vòng quanh thân cây chính là chu vi của thân cây.
- Tính đường kính của thân cây = độ dài một vòng quanh thân cây : 3,14
Lời giải chi tiết:
Ví dụ: Độ dài một vòng quanh thân cây là 150 cm.
Vậy đường kính của thân cây là:
150 : 3,14 = 47,77 (cm)
Làm tròn đến số tự nhiên ta được 48 cm.
Bài 55 trong sách giáo khoa Toán lớp 5 Cánh Diều tập trung vào việc giới thiệu và thực hành tính chu vi của hình tròn. Đây là một khái niệm quan trọng trong hình học, giúp học sinh hiểu rõ hơn về các hình dạng cơ bản và ứng dụng của chúng trong cuộc sống.
Chu vi của hình tròn là độ dài đường tròn bao quanh hình tròn đó. Để hiểu rõ hơn, ta có thể tưởng tượng như mình dùng một sợi dây để quấn quanh hình tròn, sau đó duỗi thẳng sợi dây ra, độ dài của sợi dây chính là chuvi hình tròn.
Công thức tính chu vi hình tròn là: C = πd hoặc C = 2πr, trong đó:
Để tính chu vi hình tròn, ta cần biết đường kính hoặc bán kính của hình tròn. Nếu biết bán kính, ta có thể tính đường kính bằng công thức: d = 2r.
Ví dụ 1: Một hình tròn có bán kính là 5cm. Tính chu vi của hình tròn đó.
Giải:
Chu vi của hình tròn là: C = 2πr = 2 * 3.14 * 5 = 31.4 (cm)
Ví dụ 2: Một hình tròn có đường kính là 10cm. Tính chu vi của hình tròn đó.
Giải:
Chu vi của hình tròn là: C = πd = 3.14 * 10 = 31.4 (cm)
Dưới đây là một số bài tập luyện tập để các em học sinh có thể củng cố kiến thức về chu vi hình tròn:
Chu vi hình tròn có ứng dụng rất lớn trong thực tế, ví dụ như tính độ dài của đường đi, tính lượng vật liệu cần thiết để làm các vật dụng hình tròn, v.v. Ngoài ra, kiến thức về chu vi hình tròn còn là nền tảng để học các khái niệm phức tạp hơn trong hình học, như diện tích hình tròn.
Bài học Toán lớp 5 Bài 55: Chu vi hình tròn - SGK Cánh Diều cung cấp cho học sinh những kiến thức cơ bản và quan trọng về chu vi hình tròn. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán thực tế một cách dễ dàng và hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.