Bài học Toán lớp 5 Bài 56 Diện tích hình tròn thuộc chương trình SGK Cánh Diều giúp các em học sinh nắm vững kiến thức về cách tính diện tích hình tròn. Bài học này cung cấp các công thức, ví dụ minh họa và bài tập thực hành để các em hiểu rõ hơn về khái niệm này.
Tại giaitoan.edu.vn, các em sẽ được học toán online một cách hiệu quả với bài giảng chi tiết, dễ hiểu và đáp án chính xác cho từng bài tập.
Tính diện tích của mỗi hình tròn sau: Số? Tính diện tích phần đã tô màu trong mỗi hình sau: Ba hình vuông dưới đây có cùng kích thước. Theo em, diện tích phần được tô màu ở các hình có bằng nhau không? Tại sao? Em có biết? Em hãy tính diện tích của thành giếng.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 21 SGK Toán 5 Cánh diều
Tính diện tích phần đã tô màu trong mỗi hình sau:
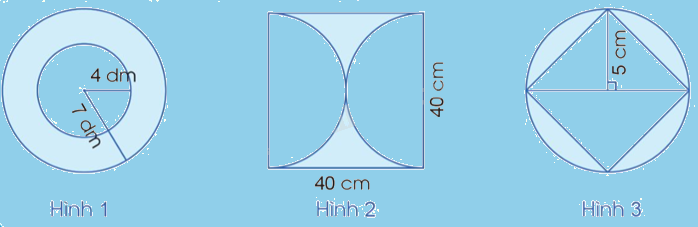
Phương pháp giải:
Tính diện tích phần đã tô màu trong mỗi hình = diện tích hình to – diện tích phần không tô màu.
Lời giải chi tiết:
* Hình 1:
Diện tích hình tròn lớn là:
$7 \times 7 \times 3,14 = 153,86$(dm2)
Diện tích hình tròn bé là:
$4 \times 4 \times 3,14 = 50,24$(dm2)
Diện tích phần đã tô màu trong hình 1 là:
153,86 – 50,24 = 103,62 (dm2)
* Hình 2:
Diện tích hình vuông là:
$40 \times 40 = 1600$(cm2)
Diện tích 2 nửa hình tròn chính là diện tích hình tròn đường kính 40 cm.
Bán kính của hình tròn là 40 : 2 = 20 (cm)
Diện tích hình tròn là
20 x 20 x 3,14 = 1256 (cm2)
Diện tích phần đã tô màu trong hình 2 là:
1600 – 1256 = 344 (cm2)
* Hình 3:
Diện tích hình tròn lớn là:
$5 \times 5 \times 3,14 = 78,5$(cm2)
Hình thoi tạo bởi hai hình tam giác.
Độ dài đáy mỗi hình tam giác là:
5 x 2 = 10 (cm)
Tổng diện tích hai hình tam giác:
$2 \times \frac{{5 \times 10}}{2} = 50$(cm2)
Diện tích phần đã tô màu trong hình 3 là:
78,5 – 50 = 28,5 (cm2)
Video hướng dẫn giải
Trả lời câu hỏi 5 trang 21 SGK Toán 5 Cánh diều
Em có biết?
Đình Yên Thái (phường Hàng Gai, quận Hoàn Kiếm, Hà Nội) là nơi thờ Nguyên phi Ỷ Lan. Trong đình hiện còn giếng cổ khơi mạch từ năm 1063, đến nay nước vẫn còn trong mát.
Miệng giếng là một hình tròn có đường kính 66 cm. Người ta xây thành giếng rộng 22 cm bao quanh miệng giếng. Em hãy tính diện tích của thành giếng.
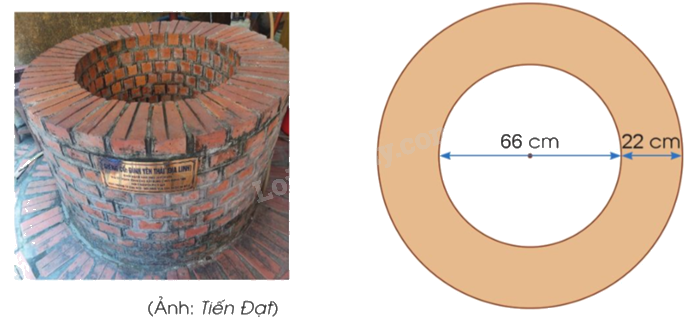
Phương pháp giải:
Tính diện tích của thành giếng = diện tích của cả miệng giếng và thành giếng – diện tích của miệng giếng nhỏ
Lời giải chi tiết:
Bán kính của miệng giếng là:
66: 2 = 33 (cm)
Bán kính của miệng giếng và thành giếng là:
33 + 22 = 55 (cm)
Diện tích của cả miệng giếng và thành giếng là:
55 x 55 x 3,14 = 9498,5 (cm2)
Diện tích của miệng giếng nhỏ là:
33 x 33 x 3,14 = 3419,46 (cm2)
Diện tích của thành giếng là:
9498,5 - 3419,46 = 6079,04 (cm2)
Đáp số: 6079,04 cm2
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 20 SGK Toán 5 Cánh diều
Tính diện tích của mỗi hình tròn sau:
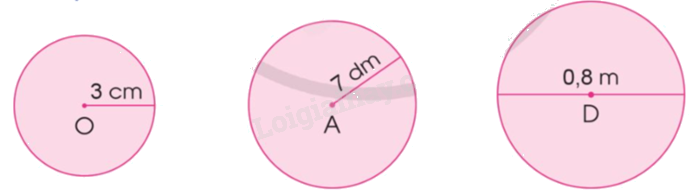
Phương pháp giải:
Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số 3,14.
$S = r \times r \times 3,14$
Lời giải chi tiết:
Diện tích của hình tròn tâm O là:
$3 \times 3 \times 3,14 = 28,26$(cm2)
Diện tích của hình tròn tâm A là:
$7 \times 7 \times 3,14 = 153,86$(dm2)
Bán kính của hình tròn tâm D là:
0,8 : 2 = 0,4 (m)
Diện tích của hình tròn tâm D là:
0,4 x 0,4 x 3,14 = 0,5024 (m2)
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 21 SGK Toán 5 Cánh diều
Ba hình vuông dưới đây có cùng kích thước. Theo em, diện tích phần được tô màu ở các hình có bằng nhau không? Tại sao?
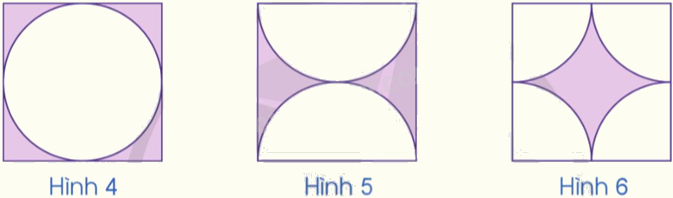
Phương pháp giải:
So sánh phần diện tích không tô màu ở các hình. Từ đó so sánh được diện tích phần tô màu ở các hình đó.
Lời giải chi tiết:
Ta thấy: Diện tích 4 nửa hình tròn của hình 6 = Diện tích của 2 nửa hình tròn của hình 5 = Diện tích hình tròn hình 4.
Nên diện tích phần được tô màu ở các hình bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 20 SGK Toán 5 Cánh diều
Số?
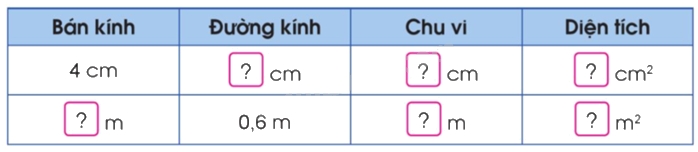
Phương pháp giải:
$S = r \times r \times 3,14$; $C = d \times 3,14$; $d = r \times 2$
Lời giải chi tiết:
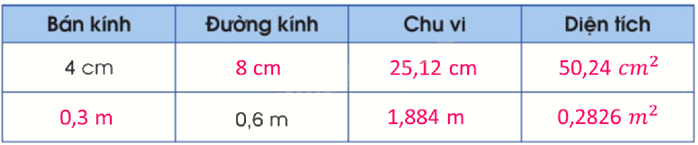
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 20 SGK Toán 5 Cánh diều
Tính diện tích của mỗi hình tròn sau:
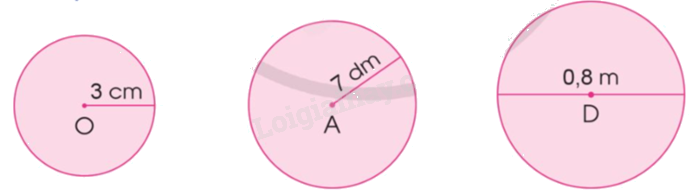
Phương pháp giải:
Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số 3,14.
$S = r \times r \times 3,14$
Lời giải chi tiết:
Diện tích của hình tròn tâm O là:
$3 \times 3 \times 3,14 = 28,26$(cm2)
Diện tích của hình tròn tâm A là:
$7 \times 7 \times 3,14 = 153,86$(dm2)
Bán kính của hình tròn tâm D là:
0,8 : 2 = 0,4 (m)
Diện tích của hình tròn tâm D là:
0,4 x 0,4 x 3,14 = 0,5024 (m2)
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 20 SGK Toán 5 Cánh diều
Số?
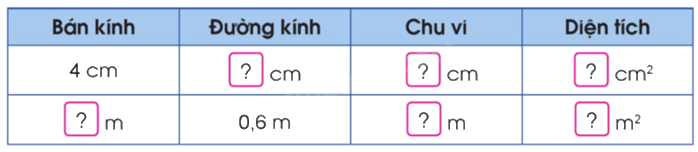
Phương pháp giải:
$S = r \times r \times 3,14$; $C = d \times 3,14$; $d = r \times 2$
Lời giải chi tiết:
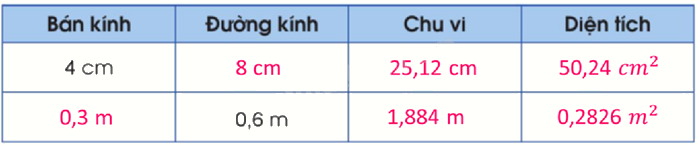
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 21 SGK Toán 5 Cánh diều
Tính diện tích phần đã tô màu trong mỗi hình sau:
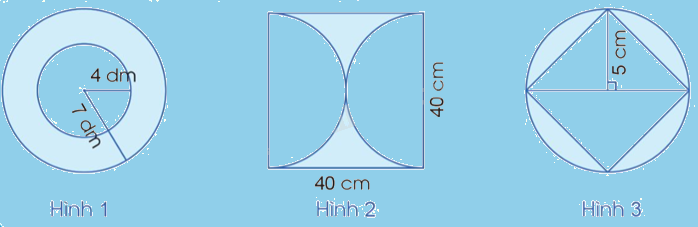
Phương pháp giải:
Tính diện tích phần đã tô màu trong mỗi hình = diện tích hình to – diện tích phần không tô màu.
Lời giải chi tiết:
* Hình 1:
Diện tích hình tròn lớn là:
$7 \times 7 \times 3,14 = 153,86$(dm2)
Diện tích hình tròn bé là:
$4 \times 4 \times 3,14 = 50,24$(dm2)
Diện tích phần đã tô màu trong hình 1 là:
153,86 – 50,24 = 103,62 (dm2)
* Hình 2:
Diện tích hình vuông là:
$40 \times 40 = 1600$(cm2)
Diện tích 2 nửa hình tròn chính là diện tích hình tròn đường kính 40 cm.
Bán kính của hình tròn là 40 : 2 = 20 (cm)
Diện tích hình tròn là
20 x 20 x 3,14 = 1256 (cm2)
Diện tích phần đã tô màu trong hình 2 là:
1600 – 1256 = 344 (cm2)
* Hình 3:
Diện tích hình tròn lớn là:
$5 \times 5 \times 3,14 = 78,5$(cm2)
Hình thoi tạo bởi hai hình tam giác.
Độ dài đáy mỗi hình tam giác là:
5 x 2 = 10 (cm)
Tổng diện tích hai hình tam giác:
$2 \times \frac{{5 \times 10}}{2} = 50$(cm2)
Diện tích phần đã tô màu trong hình 3 là:
78,5 – 50 = 28,5 (cm2)
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 21 SGK Toán 5 Cánh diều
Ba hình vuông dưới đây có cùng kích thước. Theo em, diện tích phần được tô màu ở các hình có bằng nhau không? Tại sao?
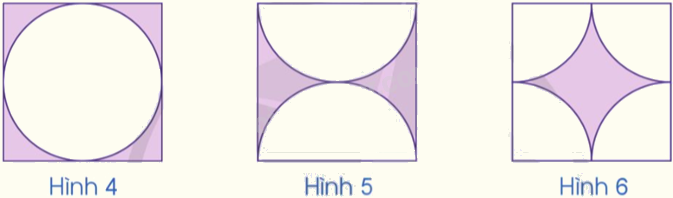
Phương pháp giải:
So sánh phần diện tích không tô màu ở các hình. Từ đó so sánh được diện tích phần tô màu ở các hình đó.
Lời giải chi tiết:
Ta thấy: Diện tích 4 nửa hình tròn của hình 6 = Diện tích của 2 nửa hình tròn của hình 5 = Diện tích hình tròn hình 4.
Nên diện tích phần được tô màu ở các hình bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi 5 trang 21 SGK Toán 5 Cánh diều
Em có biết?
Đình Yên Thái (phường Hàng Gai, quận Hoàn Kiếm, Hà Nội) là nơi thờ Nguyên phi Ỷ Lan. Trong đình hiện còn giếng cổ khơi mạch từ năm 1063, đến nay nước vẫn còn trong mát.
Miệng giếng là một hình tròn có đường kính 66 cm. Người ta xây thành giếng rộng 22 cm bao quanh miệng giếng. Em hãy tính diện tích của thành giếng.
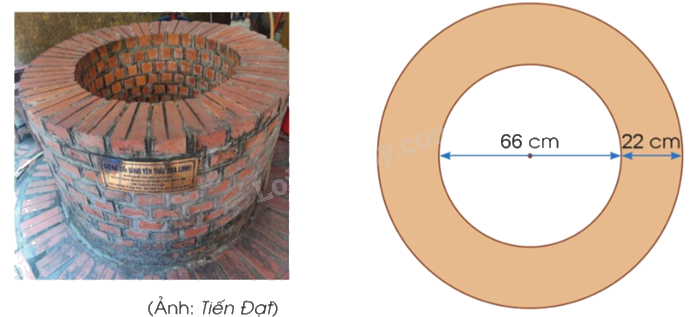
Phương pháp giải:
Tính diện tích của thành giếng = diện tích của cả miệng giếng và thành giếng – diện tích của miệng giếng nhỏ
Lời giải chi tiết:
Bán kính của miệng giếng là:
66: 2 = 33 (cm)
Bán kính của miệng giếng và thành giếng là:
33 + 22 = 55 (cm)
Diện tích của cả miệng giếng và thành giếng là:
55 x 55 x 3,14 = 9498,5 (cm2)
Diện tích của miệng giếng nhỏ là:
33 x 33 x 3,14 = 3419,46 (cm2)
Diện tích của thành giếng là:
9498,5 - 3419,46 = 6079,04 (cm2)
Đáp số: 6079,04 cm2
Bài 56 Toán lớp 5 Cánh Diều tập trung vào việc giúp học sinh hiểu và vận dụng công thức tính diện tích hình tròn. Đây là một kiến thức quan trọng trong chương trình Toán học ở tiểu học, làm nền tảng cho các kiến thức hình học phức tạp hơn ở các lớp trên.
Trước khi đi vào tính diện tích, chúng ta cần ôn lại một số kiến thức cơ bản về hình tròn:
Diện tích hình tròn được tính bằng công thức:
S = πr2
Trong đó:
Ví dụ 1: Tính diện tích của hình tròn có bán kính r = 5cm.
Giải:
Diện tích hình tròn là: S = πr2 = 3,14 x 52 = 3,14 x 25 = 78,5 cm2
Ví dụ 2: Một hình tròn có đường kính d = 10cm. Tính diện tích của hình tròn đó.
Giải:
Bán kính của hình tròn là: r = d/2 = 10/2 = 5cm
Diện tích hình tròn là: S = πr2 = 3,14 x 52 = 3,14 x 25 = 78,5 cm2
Diện tích hình tròn có ứng dụng rất lớn trong thực tế, ví dụ như tính diện tích bề mặt của các vật thể hình tròn, tính diện tích các khu vườn hình tròn, tính lượng vật liệu cần thiết để làm các sản phẩm hình tròn,...
Hy vọng bài học Toán lớp 5 Bài 56 Diện tích hình tròn - SGK Cánh Diều này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức này và tự tin giải các bài tập liên quan. Chúc các em học tốt!