Bài học Toán lớp 5 Bài 65 tập trung vào việc giúp học sinh nắm vững kiến thức về thể tích hình hộp chữ nhật và hình lập phương. Đây là một trong những kiến thức cơ bản và quan trọng trong chương trình học Hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK Cánh Diều, giúp học sinh tự tin chinh phục môn Toán.
Tính thể tích các hình sau: a) Tính thể tích mỗi đồ vật sau: b) Trong hai hộp sau, hộp nào cần dùng nhiều giấy gói hơn? Quan sát hình vẽ: a) Tính thể tích thùng hàng. b) Tính diện tích toàn phần của thùng hàng. Ước lượng rồi lựa chọn số đo thể tích phù hợp:
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 44 SGK Toán 5 Cánh diều
Tính thể tích các hình sau:

Phương pháp giải:
Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).
$V = a \times b \times c$
Muốn tính thể tích hình lập phương, ta lấy cạnh nhân với cạnh rồi nhân với cạnh (cùng một đơn vị đo).
$V = a \times a \times a$
Lời giải chi tiết:
a) Thể tích hình hộp chữ nhật đó là:
$5 \times 8 \times 5 = 200$(cm3)
Đáp số: 200 cm3
b) Thể tích hình lập phương đó là:
$4 \times 4 \times 4 = 64$(dm3)
Đáp số: 64 dm3
c) Thể tích hình hộp chữ nhật đó là:
$20 \times 4 \times 5 = 400$(m3)
Đáp số: 400 m3.
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 45 SGK Toán 5 Cánh diều
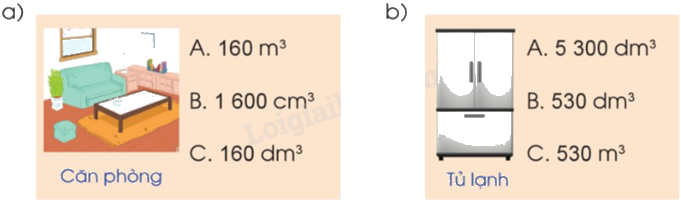
Ước lượng rồi lựa chọn số đo thể tích phù hợp:
Phương pháp giải:
Ước lượng rồi lựa chọn số đo thể tích phù hợp.
Lời giải chi tiết:
a) Căn phòng có thể tích là 160 m3.
Chọn A.
b) Tủ lạnh có thể tích là 530 dm3.
Chọn B.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 45 SGK Toán 5 Cánh diều
a) Tính thể tích mỗi đồ vật sau:
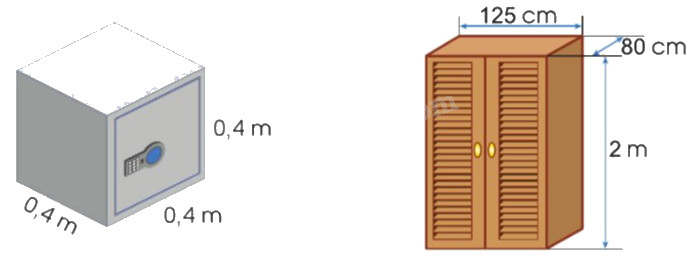
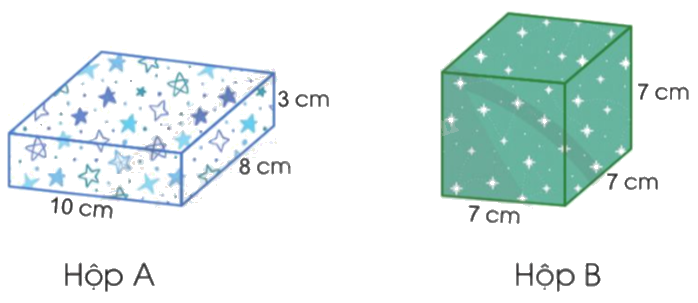
b) Trong hai hộp sau, hộp nào cần dùng nhiều giấy gói hơn?

Phương pháp giải:
a) Thể tích hình hộp chữ nhật: $V = a \times b \times c$
Thể tích hình lập phương: $V = a \times a \times a$
b) Tính thể tích hai hộp rồi so sánh thể tích hộp nào lớn hơn thì cần dùng nhiều giấy gói hơn.
Lời giải chi tiết:
a) Thể tích cái két sắt là:
$0,4 \times 0,4 \times 0,4 = 0,064$(m3)
Đổi: 125 cm = 1,25 m; 80 cm = 0,8 m.
Thể tích cái tủ gỗ là:
$1,25 \times 0,8 \times 2 = 2$(m3)
b) Diện tích xung quanh của hộp A là:
(10 + 8) x 2 x 3 = 108 (cm2)
Diện tích toàn phần của hộp A là:
10 x 8 x 2 + 108 = 268 (cm2)
Diện tích toàn phần của hộp B là:
7 x 7 x 6 = 294 (cm2)
Vì 294 cm2 > 268 cm2
Nên hộp B cần dùng nhiều giấy gói hơn.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 45 SGK Toán 5 Cánh diều
Quan sát hình vẽ:
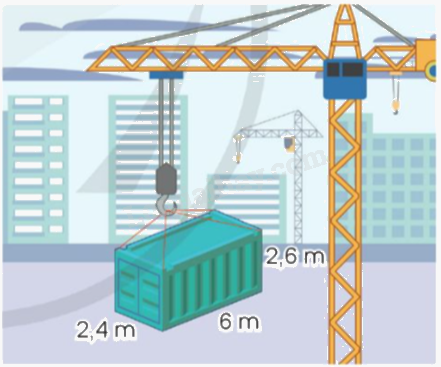
a) Tính thể tích thùng hàng.
b) Tính diện tích toàn phần của thùng hàng.
Phương pháp giải:
a) Tính thể tích thùng hàng bằng chiều dài $ \times $chiều rộng $ \times $chiều cao.
b) Tính diện tích toàn phần của thùng hàng = diện tích xung quanh + 2 $ \times $diện tích đáy
- Diện tích đáy = chiều dài $ \times $chiều rộng
- Diện tích xung quanh = chu vi đáy $ \times $chiều cao
Lời giải chi tiết:
a) Thể tích thùng hàng đó là:
$2,4 \times 6 \times 2,6 = 37,44$(m3)
b) Diện tích xung quanh của thùng hàng là:
$\left( {2,4 + 6} \right) \times 2 \times 2,6 = 43,68$(m2)
Diện tích toàn phần của thùng hàng là:
43,68 + 6 x 2,4 x 2 = 72,48 (m2)
Đáp số: a) 37,44 m3;
b) 72,48 m2.
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 44 SGK Toán 5 Cánh diều
Tính thể tích các hình sau:

Phương pháp giải:
Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).
$V = a \times b \times c$
Muốn tính thể tích hình lập phương, ta lấy cạnh nhân với cạnh rồi nhân với cạnh (cùng một đơn vị đo).
$V = a \times a \times a$
Lời giải chi tiết:
a) Thể tích hình hộp chữ nhật đó là:
$5 \times 8 \times 5 = 200$(cm3)
Đáp số: 200 cm3
b) Thể tích hình lập phương đó là:
$4 \times 4 \times 4 = 64$(dm3)
Đáp số: 64 dm3
c) Thể tích hình hộp chữ nhật đó là:
$20 \times 4 \times 5 = 400$(m3)
Đáp số: 400 m3.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 45 SGK Toán 5 Cánh diều
a) Tính thể tích mỗi đồ vật sau:
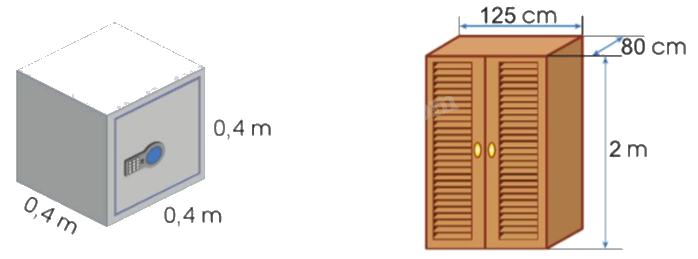
b) Trong hai hộp sau, hộp nào cần dùng nhiều giấy gói hơn?
Phương pháp giải:
a) Thể tích hình hộp chữ nhật: $V = a \times b \times c$
Thể tích hình lập phương: $V = a \times a \times a$
b) Tính thể tích hai hộp rồi so sánh thể tích hộp nào lớn hơn thì cần dùng nhiều giấy gói hơn.
Lời giải chi tiết:
a) Thể tích cái két sắt là:
$0,4 \times 0,4 \times 0,4 = 0,064$(m3)
Đổi: 125 cm = 1,25 m; 80 cm = 0,8 m.
Thể tích cái tủ gỗ là:
$1,25 \times 0,8 \times 2 = 2$(m3)
b) Diện tích xung quanh của hộp A là:
(10 + 8) x 2 x 3 = 108 (cm2)
Diện tích toàn phần của hộp A là:
10 x 8 x 2 + 108 = 268 (cm2)
Diện tích toàn phần của hộp B là:
7 x 7 x 6 = 294 (cm2)
Vì 294 cm2 > 268 cm2
Nên hộp B cần dùng nhiều giấy gói hơn.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 45 SGK Toán 5 Cánh diều
Quan sát hình vẽ:
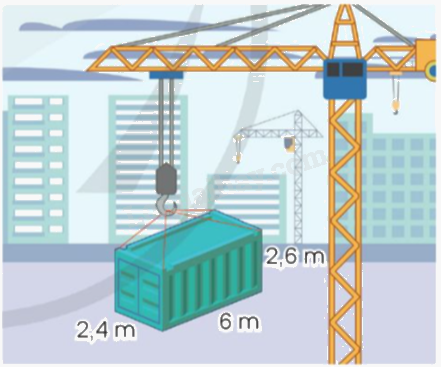
a) Tính thể tích thùng hàng.
b) Tính diện tích toàn phần của thùng hàng.
Phương pháp giải:
a) Tính thể tích thùng hàng bằng chiều dài $ \times $chiều rộng $ \times $chiều cao.
b) Tính diện tích toàn phần của thùng hàng = diện tích xung quanh + 2 $ \times $diện tích đáy
- Diện tích đáy = chiều dài $ \times $chiều rộng
- Diện tích xung quanh = chu vi đáy $ \times $chiều cao
Lời giải chi tiết:
a) Thể tích thùng hàng đó là:
$2,4 \times 6 \times 2,6 = 37,44$(m3)
b) Diện tích xung quanh của thùng hàng là:
$\left( {2,4 + 6} \right) \times 2 \times 2,6 = 43,68$(m2)
Diện tích toàn phần của thùng hàng là:
43,68 + 6 x 2,4 x 2 = 72,48 (m2)
Đáp số: a) 37,44 m3;
b) 72,48 m2.
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 45 SGK Toán 5 Cánh diều
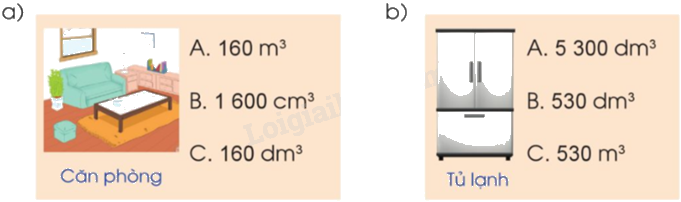
Ước lượng rồi lựa chọn số đo thể tích phù hợp:
Phương pháp giải:
Ước lượng rồi lựa chọn số đo thể tích phù hợp.
Lời giải chi tiết:
a) Căn phòng có thể tích là 160 m3.
Chọn A.
b) Tủ lạnh có thể tích là 530 dm3.
Chọn B.
Bài 65 Toán lớp 5 thuộc chương trình Hình học, tập trung vào việc củng cố kiến thức về thể tích của hai hình khối quan trọng: hình hộp chữ nhật và hình lập phương. Việc hiểu rõ công thức và cách áp dụng vào giải bài tập là yếu tố then chốt để học sinh đạt kết quả tốt.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các khái niệm và công thức sau:
Dưới đây là hướng dẫn giải chi tiết các bài tập trong SGK Cánh Diều:
Bài tập này yêu cầu học sinh áp dụng công thức V = a x b x c để tính thể tích của các hình hộp chữ nhật khác nhau. Lưu ý, cần xác định đúng các giá trị a, b, c từ dữ liệu đề bài.
Tương tự như bài 1, học sinh sử dụng công thức V = a3 để tính thể tích của hình lập phương. Đảm bảo đơn vị đo được thống nhất trước khi tính toán.
Bài tập này thường yêu cầu học sinh giải quyết các bài toán thực tế liên quan đến thể tích hình hộp chữ nhật và hình lập phương, ví dụ như tính lượng nước cần để đổ đầy một bể bơi hình hộp chữ nhật, hoặc tính thể tích của một hộp quà hình lập phương.
Ngoài việc nắm vững công thức, học sinh cũng nên hiểu rõ mối liên hệ giữa thể tích và các yếu tố hình học khác như diện tích đáy và chiều cao. Điều này sẽ giúp học sinh giải quyết các bài toán phức tạp hơn một cách dễ dàng.
Để củng cố kiến thức, học sinh có thể tự giải thêm các bài tập tương tự từ các nguồn tài liệu khác nhau. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Một hình hộp chữ nhật có chiều dài 8cm, chiều rộng 5cm và chiều cao 3cm. Tính thể tích của hình hộp chữ nhật đó.
Giải:
Thể tích của hình hộp chữ nhật là: V = 8cm x 5cm x 3cm = 120cm3
Toán lớp 5 Bài 65 là một bài học quan trọng giúp học sinh làm quen với khái niệm thể tích và cách tính thể tích của hai hình khối cơ bản. Việc nắm vững kiến thức này sẽ là nền tảng vững chắc cho các bài học Hình học nâng cao hơn trong tương lai. Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ khi gặp khó khăn.