Bài học Toán lớp 4 trang 60 - Bài 56: Rút gọn phân số thuộc chương trình Kết nối tri thức giúp các em học sinh nắm vững kiến thức về phân số và cách rút gọn chúng. Bài học này rất quan trọng để xây dựng nền tảng toán học vững chắc.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong sách giáo khoa, giúp các em tự tin giải toán và đạt kết quả tốt nhất.
Rút gọn mỗi phân số ghi ở bông hoa được phân số nào ghi ở lọ hoa?Thỏ mẹ chia một giỏ cà rốt cho các con. Thỏ nâu được 5/10 giỏ
Video hướng dẫn giải
Chọn câu trả lời đúng.
Rút gọn phân số $\frac{{48}}{{60}}$ được phân số tối giản là:
A. $\frac{{24}}{{30}}$
B.$\frac{{12}}{{15}}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
Ta có: $\frac{{48}}{{60}} = \frac{{48:12}}{{60:12}} = \frac{4}{5}$
Chọn đáp án D
Video hướng dẫn giải
Thỏ mẹ chia một giỏ cà rốt cho các con. Thỏ nâu được $\frac{5}{{10}}$ giỏ, thỏ xám được $\frac{1}{4}$ giỏ, thỏ trắng được $\frac{{25}}{{100}}$giỏ. Hỏi hai thỏ con nào được thỏ mẹ chia cho số phần giỏ cà rốt bằng nhau?
Phương pháp giải:
- Rút gọn các phân số chưa tối giản
- Kết luận hai thỏ con được thỏ mẹ chia cho số phần giỏ cà rốt bằng nhau.
Lời giải chi tiết:
$\frac{5}{{10}} = \frac{{5:5}}{{10:5}} = \frac{1}{2}$
$\frac{{25}}{{100}} = \frac{{25:25}}{{100:25}} = \frac{1}{4}$
Vậy thỏ xám và thỏ trắng được thỏ mẹ chia cho số phần giỏ cà rốt bằng nhau.
>> Xem chi tiết: Lý thuyết: Bài 56. Rút gọn phân số - SGK Kết nối tri thức
Video hướng dẫn giải
a) Trong các phân số: $\frac{2}{3};\frac{9}{{21}};\frac{5}{{17}};\frac{1}{{10}};\frac{{10}}{{15}};\frac{7}{{14}}$ phân số nào tối giản, phân số nào chưa tối giản?
b) Rút gọn các phân số chưa tối giản ở câu a (theo mẫu).
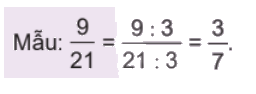
Phương pháp giải:
a)Phân số tối giản là phân số mà tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
b) Cách rút gọn phân số:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a) Các phân số tối giản là: $\frac{2}{3};\frac{5}{{17}};\frac{1}{{10}}$
Các phân số chưa tối giản là: $\frac{9}{{21}};\frac{{10}}{{15}};\frac{7}{{14}}$
b) $\frac{9}{{21}} = \frac{{9:3}}{{21:3}} = \frac{3}{7}$
$\frac{{10}}{{15}} = \frac{{10:5}}{{15:5}} = \frac{2}{3}$
$\frac{7}{{14}} = \frac{{7:7}}{{14:7}} = \frac{1}{2}$
Video hướng dẫn giải
a) Số?
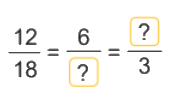
b) Rút gọn các phân số: $\frac{{12}}{{48}};\frac{{80}}{{100}};\frac{{75}}{{125}}$
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
a)
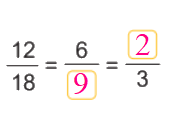
b) $\frac{{12}}{{48}} = \frac{{12:12}}{{48:12}} = \frac{1}{4}$
$\frac{{80}}{{100}} = \frac{{80:20}}{{100:20}} = \frac{4}{5}$
$\frac{{75}}{{125}} = \frac{{75:25}}{{125:25}} = \frac{3}{5}$
Video hướng dẫn giải
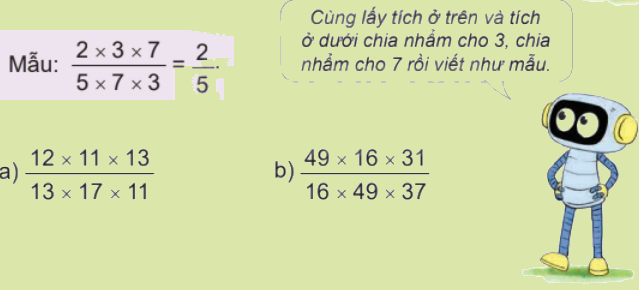
Tính (theo mẫu).
Phương pháp giải:
Cùng chia nhẩm tích ở trên và tích ở dưới cho các thừa số giống nhau.
Lời giải chi tiết:
a) $\frac{{12 \times 11 \times 13}}{{13 \times 17 \times 11}} = \frac{{12}}{{17}}$
b) \(\frac{{49 \times 16 \times 31}}{{16 \times 49 \times 37}} = \frac{{31}}{{37}}\)
Video hướng dẫn giải
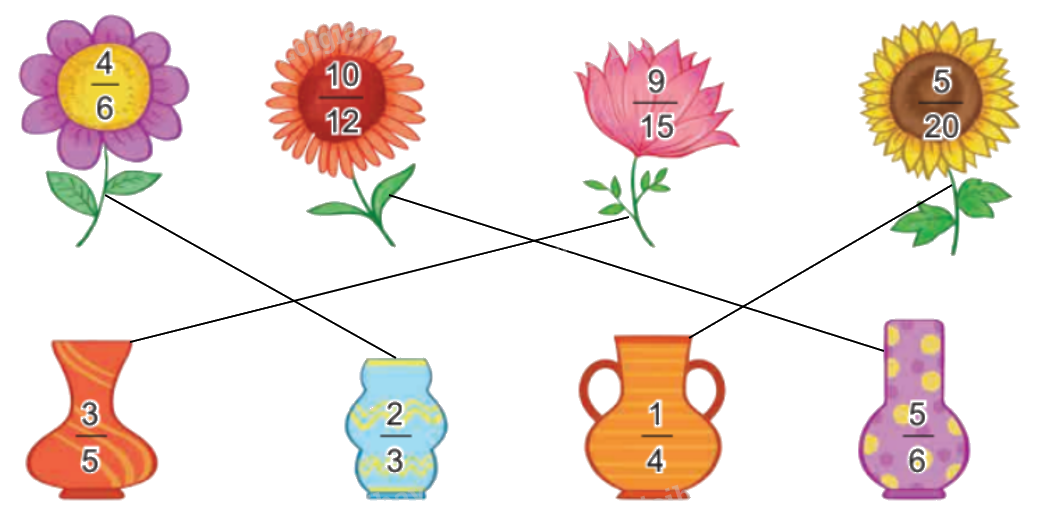
Rút gọn mỗi phân số ghi ở bông hoa được phân số nào ghi ở lọ hoa?

Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
$\frac{4}{6} = \frac{{4:2}}{{6:2}} = \frac{2}{3}$
$\frac{{10}}{{12}} = \frac{{10:2}}{{12:2}} = \frac{5}{6}$
$\frac{9}{{15}} = \frac{{9:3}}{{15:3}} = \frac{3}{5}$
$\frac{5}{{20}} = \frac{{5:5}}{{20:5}} = \frac{1}{4}$
Ta có kết quả như sau:
Video hướng dẫn giải
a) Trong các phân số: $\frac{2}{3};\frac{9}{{21}};\frac{5}{{17}};\frac{1}{{10}};\frac{{10}}{{15}};\frac{7}{{14}}$ phân số nào tối giản, phân số nào chưa tối giản?
b) Rút gọn các phân số chưa tối giản ở câu a (theo mẫu).
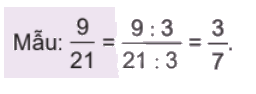
Phương pháp giải:
a)Phân số tối giản là phân số mà tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
b) Cách rút gọn phân số:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a) Các phân số tối giản là: $\frac{2}{3};\frac{5}{{17}};\frac{1}{{10}}$
Các phân số chưa tối giản là: $\frac{9}{{21}};\frac{{10}}{{15}};\frac{7}{{14}}$
b) $\frac{9}{{21}} = \frac{{9:3}}{{21:3}} = \frac{3}{7}$
$\frac{{10}}{{15}} = \frac{{10:5}}{{15:5}} = \frac{2}{3}$
$\frac{7}{{14}} = \frac{{7:7}}{{14:7}} = \frac{1}{2}$
Video hướng dẫn giải
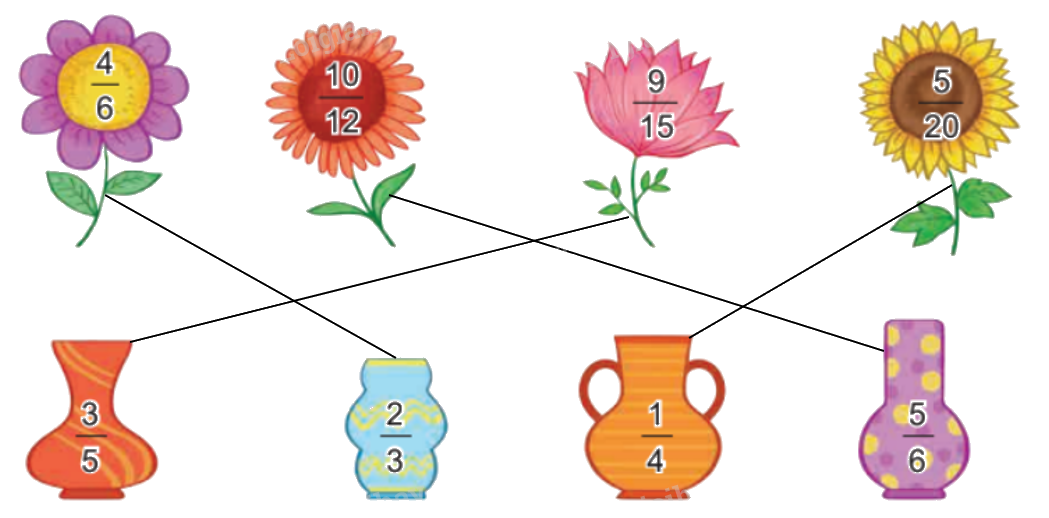
Rút gọn mỗi phân số ghi ở bông hoa được phân số nào ghi ở lọ hoa?

Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
$\frac{4}{6} = \frac{{4:2}}{{6:2}} = \frac{2}{3}$
$\frac{{10}}{{12}} = \frac{{10:2}}{{12:2}} = \frac{5}{6}$
$\frac{9}{{15}} = \frac{{9:3}}{{15:3}} = \frac{3}{5}$
$\frac{5}{{20}} = \frac{{5:5}}{{20:5}} = \frac{1}{4}$
Ta có kết quả như sau:
Video hướng dẫn giải
a) Số?
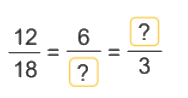
b) Rút gọn các phân số: $\frac{{12}}{{48}};\frac{{80}}{{100}};\frac{{75}}{{125}}$
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
a)
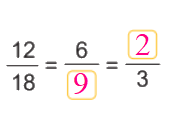
b) $\frac{{12}}{{48}} = \frac{{12:12}}{{48:12}} = \frac{1}{4}$
$\frac{{80}}{{100}} = \frac{{80:20}}{{100:20}} = \frac{4}{5}$
$\frac{{75}}{{125}} = \frac{{75:25}}{{125:25}} = \frac{3}{5}$
Video hướng dẫn giải
Chọn câu trả lời đúng.
Rút gọn phân số $\frac{{48}}{{60}}$ được phân số tối giản là:
A. $\frac{{24}}{{30}}$
B.$\frac{{12}}{{15}}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
Ta có: $\frac{{48}}{{60}} = \frac{{48:12}}{{60:12}} = \frac{4}{5}$
Chọn đáp án D
Video hướng dẫn giải
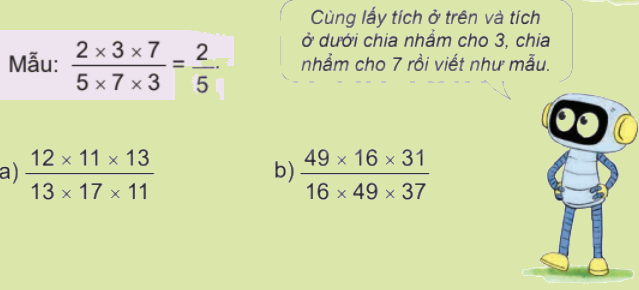
Tính (theo mẫu).
Phương pháp giải:
Cùng chia nhẩm tích ở trên và tích ở dưới cho các thừa số giống nhau.
Lời giải chi tiết:
a) $\frac{{12 \times 11 \times 13}}{{13 \times 17 \times 11}} = \frac{{12}}{{17}}$
b) \(\frac{{49 \times 16 \times 31}}{{16 \times 49 \times 37}} = \frac{{31}}{{37}}\)
Video hướng dẫn giải
Thỏ mẹ chia một giỏ cà rốt cho các con. Thỏ nâu được $\frac{5}{{10}}$ giỏ, thỏ xám được $\frac{1}{4}$ giỏ, thỏ trắng được $\frac{{25}}{{100}}$giỏ. Hỏi hai thỏ con nào được thỏ mẹ chia cho số phần giỏ cà rốt bằng nhau?
Phương pháp giải:
- Rút gọn các phân số chưa tối giản
- Kết luận hai thỏ con được thỏ mẹ chia cho số phần giỏ cà rốt bằng nhau.
Lời giải chi tiết:
$\frac{5}{{10}} = \frac{{5:5}}{{10:5}} = \frac{1}{2}$
$\frac{{25}}{{100}} = \frac{{25:25}}{{100:25}} = \frac{1}{4}$
Vậy thỏ xám và thỏ trắng được thỏ mẹ chia cho số phần giỏ cà rốt bằng nhau.
>> Xem chi tiết: Lý thuyết: Bài 56. Rút gọn phân số - SGK Kết nối tri thức
Bài 56 trong sách Toán lớp 4 Kết nối tri thức tập trung vào việc củng cố kỹ năng rút gọn phân số. Đây là một trong những kiến thức cơ bản và quan trọng trong chương trình học Toán tiểu học, giúp học sinh hiểu rõ hơn về cấu trúc và tính chất của phân số.
Rút gọn phân số là việc chia cả tử số và mẫu số của phân số cho một ước chung lớn nhất của chúng. Mục đích của việc rút gọn phân số là để biểu diễn phân số ở dạng đơn giản nhất, tức là tử số và mẫu số không còn ước chung nào khác ngoài 1.
Ví dụ 1: Rút gọn phân số 12/18
Ví dụ 2: Rút gọn phân số 25/35
Dưới đây là một số bài tập trong sách giáo khoa Toán lớp 4 trang 60 - Bài 56 để các em luyện tập:
| Phân số | Phân số rút gọn |
|---|---|
| 8/12 | 2/3 |
| 15/20 | 3/4 |
| 16/24 | 2/3 |
| 9/12 | 3/4 |
Ngoài việc rút gọn phân số, các em cũng cần làm quen với các phép toán khác liên quan đến phân số như cộng, trừ, nhân, chia phân số. Việc nắm vững các kiến thức này sẽ giúp các em giải quyết các bài toán phức tạp hơn trong tương lai.
Hy vọng với những kiến thức và ví dụ minh họa trên, các em học sinh lớp 4 sẽ hiểu rõ hơn về cách rút gọn phân số và tự tin giải các bài tập trong sách giáo khoa Toán lớp 4 trang 60 - Bài 56 - SGK Kết nối tri thức.