Bài học Toán lớp 4 trang 91 thuộc chương trình Kết nối tri thức tập trung vào việc giúp học sinh nắm vững kiến thức về phép chia phân số. Bài học này cung cấp các ví dụ minh họa và bài tập thực hành để học sinh có thể áp dụng kiến thức vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong sách giáo khoa Toán lớp 4 trang 91, giúp học sinh tự học hiệu quả và đạt kết quả tốt nhất.
Một bức tranh hình chữ nhật có diện tích 27/2 Người ta cắt một thanh sắt dài 3/2 m thành các đoạn
Video hướng dẫn giải
Tìm phân số thích hợp.
Một bức tranh hình chữ nhật có diện tích $\frac{{27}}{2}$dm2 và chiều rộng $\frac{{10}}{3}$dm.
Chiều dài của bức tranh là ..?.. dm.
Phương pháp giải:
Chiều dài bức tranh = diện tích bức tranh : chiều rộng
Lời giải chi tiết:
Chiều dài bức tranh là: $\frac{{27}}{2}:\frac{{10}}{3} = \frac{{81}}{{20}}$ (dm)
Vậy phân số thích hợp cần tìm là $\frac{{81}}{{20}}$
>> Xem chi tiết: Lý thuyết: Bài 64. Phép chia phân số - SGK Kết nối tri thức
Video hướng dẫn giải
a) Viết phân số đảo ngược của mỗi phân số sau: $\frac{5}{8};\,\,\frac{3}{4};\,\,\frac{1}{2}$
b) Tính.
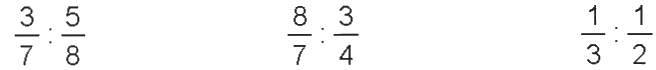
Phương pháp giải:
a) Viết phân số đảo ngược của mỗi phân số đã cho
b)Muốn thực hiện phép chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai
Lời giải chi tiết:
a) Phân số đảo ngược của mỗi phân số sau: $\frac{5}{8};\,\,\frac{3}{4};\,\,\frac{1}{2}$ lần lượt là $\frac{8}{5};\,\,\frac{4}{3};\,\,\frac{2}{1}$
b) \(\frac{3}{7}:\frac{5}{8} = \frac{3}{7} \times \frac{8}{5} = \frac{{24}}{{35}}\,\)
\(\,\frac{8}{7}:\frac{3}{4} = \frac{8}{7} \times \frac{4}{3} = \frac{{32}}{{21}}\,\)
\(\,\frac{1}{3}:\frac{1}{2} = \frac{1}{3} \times \frac{2}{1} = \frac{2}{3}\)
Video hướng dẫn giải
Tính rồi rút gọn.
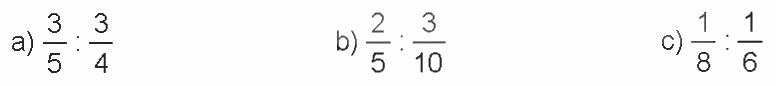
Phương pháp giải:
- Muốn thực hiện phép chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai
- Rút gọn các kết quả chưa tối giản.
Lời giải chi tiết:
a) \(\frac{3}{5}:\frac{3}{4} = \frac{3}{5} \times \frac{4}{3} = \frac{{12}}{{15}} = \frac{4}{3}\,\)
b) \(\,\frac{2}{5}:\frac{3}{{10}} = \frac{2}{5} \times \frac{{10}}{3} = \frac{{20}}{{15}} = \frac{4}{3}\)
c) \(\frac{1}{8}:\frac{1}{6} = \frac{1}{8} \times \frac{6}{1} = \frac{6}{8} = \frac{3}{4}\)
Video hướng dẫn giải
Tính rồi rút gọn.
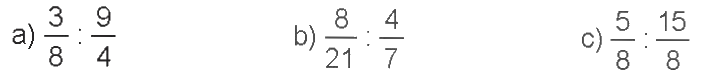
Phương pháp giải:
- Muốn thực hiện phép chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai
- Rút gọn các kết quả chưa tối giản.
Lời giải chi tiết:
a) \(\frac{3}{8}:\frac{9}{4} = \frac{3}{8} \times \frac{4}{9} = \frac{{12}}{{72}} = \frac{1}{6}\)
b) \(\frac{8}{{21}}:\frac{4}{7} = \frac{8}{{21}} \times \frac{7}{4} = \frac{{56}}{{84}} = \frac{2}{3}\,\)
c) \(\frac{5}{8}:\frac{{15}}{8} = \frac{5}{8} \times \frac{8}{{15}} = \frac{{40}}{{120}} = \frac{1}{3}\)
Video hướng dẫn giải
Tính.

Phương pháp giải:
- Biểu thức có dấu ngoặc thì thực hiện phép tính trong ngoặc trước - Biểu thức có chứa các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, thực hiện phép tính cộng, trừ sau.
Lời giải chi tiết:
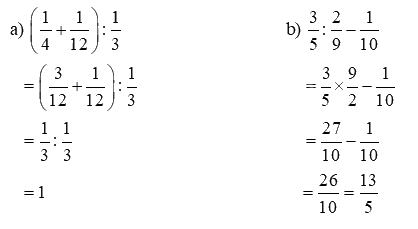
Video hướng dẫn giải
Tìm phân số thích hợp (theo mẫu).
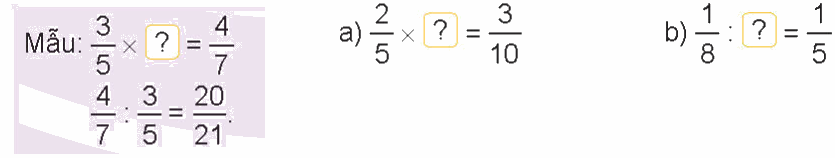
Phương pháp giải:
Để tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết
Để tìm số chia ta thấy số bị chia chia cho thương
Lời giải chi tiết:
a) \(\frac{2}{5} \times ? = \frac{3}{{10}}\,\)
\(\frac{3}{{10}}:\frac{2}{5} = \frac{3}{4}\)
b) \(\,\frac{1}{8}:? = \frac{1}{5}\)
\(\frac{1}{8}:\frac{1}{5} = \frac{5}{8}\)
Video hướng dẫn giải
Tìm phân số thích hợp.
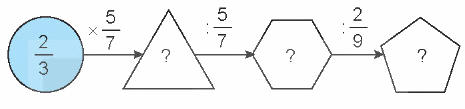
Phương pháp giải:
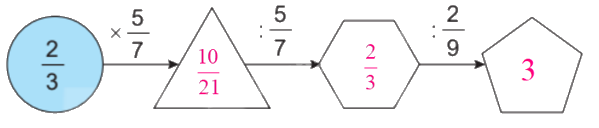
Thực hiện tính kết quả các phép tính theo chiều mũi tên rồi điền phân số thích hợp vào ô trống.
Lời giải chi tiết:
$\frac{2}{3} \times \frac{5}{7} = \frac{{2 \times 5}}{{3 \times 7}} = \frac{{10}}{{21}}$
$\frac{{10}}{{21}}:\frac{5}{7} = \frac{{10}}{{21}} \times \frac{7}{5} = \frac{{70}}{{105}} = \frac{2}{3}$
$\frac{2}{3}:\frac{2}{9} = \frac{2}{3} \times \frac{9}{2} = \frac{{18}}{6} = 3$
Video hướng dẫn giải
Người ta cắt một thanh sắt dài $\frac{3}{2}$m thành các đoạn, mỗi đoạn dài $\frac{1}{8}$m. Hỏi người ta cắt được bao nhiêu đoạn như vậy?
Phương pháp giải:
Số đoạn cắt được = độ dài thanh sắt : độ dài mỗi đoạn thanh sắt
Lời giải chi tiết:
Tóm tắt:
$\frac{1}{8}$m: 1 đoạn
$\frac{3}{2}$m: ? đoạn
Bài giải
Thanh sắt được cắt làm số đoạn là:
$\frac{3}{2}:\frac{1}{8} = 12$(đoạn)
Đáp số: 12 đoạn
Video hướng dẫn giải
Vào một buổi chiều, người ta đo được chiều dài cái bóng của ngọn tháp là $\frac{{99}}{4}$m. Biết chiều dài cái bóng của ngọn tháp gấp 2 lần chiều cao ngọn tháp. Tính chiều cao ngọn tháp.

Phương pháp giải:
Chiều cao ngọn tháp = chiều dài cái bóng : 2
Lời giải chi tiết:
Chiều cao ngọn tháp là:
$\frac{{99}}{4}:2 = \frac{{99}}{8}$ (m)
Đáp số: $\frac{{99}}{8}$ m
Video hướng dẫn giải
Tính (theo mẫu).

Phương pháp giải:
Thực hiện các phép chia theo ví dụ mẫu
Lời giải chi tiết:
a) \(3:\frac{5}{7} = \frac{{3 \times 7}}{5}{\text{ = }}\frac{{21}}{5}\)
b) \(\,4:\frac{1}{3} = \frac{{4 \times 3}}{1} = 12\)
c) \(\frac{5}{7}:3 = \frac{5}{{7 \times 3}} = \frac{5}{{21}}\,\)
Video hướng dẫn giải
a) Viết phân số đảo ngược của mỗi phân số sau: $\frac{5}{8};\,\,\frac{3}{4};\,\,\frac{1}{2}$
b) Tính.
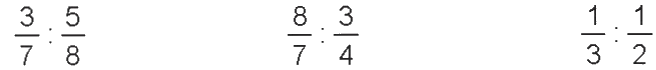
Phương pháp giải:
a) Viết phân số đảo ngược của mỗi phân số đã cho
b)Muốn thực hiện phép chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai
Lời giải chi tiết:
a) Phân số đảo ngược của mỗi phân số sau: $\frac{5}{8};\,\,\frac{3}{4};\,\,\frac{1}{2}$ lần lượt là $\frac{8}{5};\,\,\frac{4}{3};\,\,\frac{2}{1}$
b) \(\frac{3}{7}:\frac{5}{8} = \frac{3}{7} \times \frac{8}{5} = \frac{{24}}{{35}}\,\)
\(\,\frac{8}{7}:\frac{3}{4} = \frac{8}{7} \times \frac{4}{3} = \frac{{32}}{{21}}\,\)
\(\,\frac{1}{3}:\frac{1}{2} = \frac{1}{3} \times \frac{2}{1} = \frac{2}{3}\)
Video hướng dẫn giải
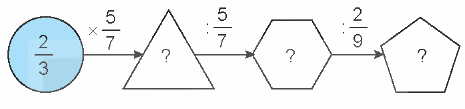
Tìm phân số thích hợp.
Phương pháp giải:
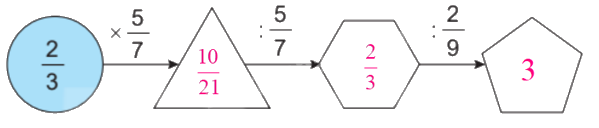
Thực hiện tính kết quả các phép tính theo chiều mũi tên rồi điền phân số thích hợp vào ô trống.
Lời giải chi tiết:
$\frac{2}{3} \times \frac{5}{7} = \frac{{2 \times 5}}{{3 \times 7}} = \frac{{10}}{{21}}$
$\frac{{10}}{{21}}:\frac{5}{7} = \frac{{10}}{{21}} \times \frac{7}{5} = \frac{{70}}{{105}} = \frac{2}{3}$
$\frac{2}{3}:\frac{2}{9} = \frac{2}{3} \times \frac{9}{2} = \frac{{18}}{6} = 3$
Video hướng dẫn giải
Tìm phân số thích hợp.
Một bức tranh hình chữ nhật có diện tích $\frac{{27}}{2}$dm2 và chiều rộng $\frac{{10}}{3}$dm.
Chiều dài của bức tranh là ..?.. dm.
Phương pháp giải:
Chiều dài bức tranh = diện tích bức tranh : chiều rộng
Lời giải chi tiết:
Chiều dài bức tranh là: $\frac{{27}}{2}:\frac{{10}}{3} = \frac{{81}}{{20}}$ (dm)
Vậy phân số thích hợp cần tìm là $\frac{{81}}{{20}}$
Video hướng dẫn giải
Tính rồi rút gọn.
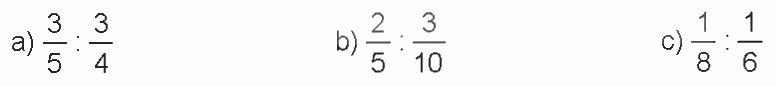
Phương pháp giải:
- Muốn thực hiện phép chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai
- Rút gọn các kết quả chưa tối giản.
Lời giải chi tiết:
a) \(\frac{3}{5}:\frac{3}{4} = \frac{3}{5} \times \frac{4}{3} = \frac{{12}}{{15}} = \frac{4}{3}\,\)
b) \(\,\frac{2}{5}:\frac{3}{{10}} = \frac{2}{5} \times \frac{{10}}{3} = \frac{{20}}{{15}} = \frac{4}{3}\)
c) \(\frac{1}{8}:\frac{1}{6} = \frac{1}{8} \times \frac{6}{1} = \frac{6}{8} = \frac{3}{4}\)
Video hướng dẫn giải
Tìm phân số thích hợp (theo mẫu).
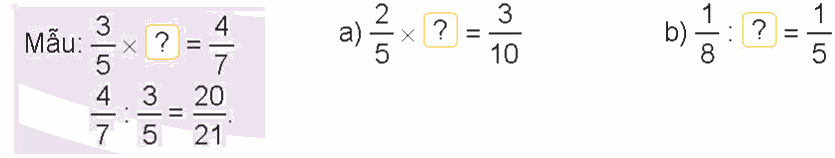
Phương pháp giải:
Để tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết
Để tìm số chia ta thấy số bị chia chia cho thương
Lời giải chi tiết:
a) \(\frac{2}{5} \times ? = \frac{3}{{10}}\,\)
\(\frac{3}{{10}}:\frac{2}{5} = \frac{3}{4}\)
b) \(\,\frac{1}{8}:? = \frac{1}{5}\)
\(\frac{1}{8}:\frac{1}{5} = \frac{5}{8}\)
Video hướng dẫn giải
Tính.

Phương pháp giải:
- Biểu thức có dấu ngoặc thì thực hiện phép tính trong ngoặc trước - Biểu thức có chứa các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, thực hiện phép tính cộng, trừ sau.
Lời giải chi tiết:
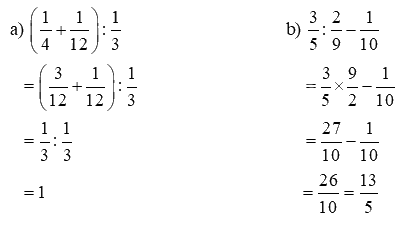
Video hướng dẫn giải
Người ta cắt một thanh sắt dài $\frac{3}{2}$m thành các đoạn, mỗi đoạn dài $\frac{1}{8}$m. Hỏi người ta cắt được bao nhiêu đoạn như vậy?
Phương pháp giải:
Số đoạn cắt được = độ dài thanh sắt : độ dài mỗi đoạn thanh sắt
Lời giải chi tiết:
Tóm tắt:
$\frac{1}{8}$m: 1 đoạn
$\frac{3}{2}$m: ? đoạn
Bài giải
Thanh sắt được cắt làm số đoạn là:
$\frac{3}{2}:\frac{1}{8} = 12$(đoạn)
Đáp số: 12 đoạn
Video hướng dẫn giải
Tính rồi rút gọn.
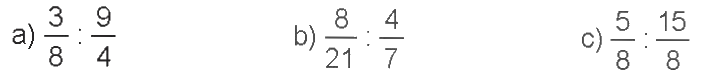
Phương pháp giải:
- Muốn thực hiện phép chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai
- Rút gọn các kết quả chưa tối giản.
Lời giải chi tiết:
a) \(\frac{3}{8}:\frac{9}{4} = \frac{3}{8} \times \frac{4}{9} = \frac{{12}}{{72}} = \frac{1}{6}\)
b) \(\frac{8}{{21}}:\frac{4}{7} = \frac{8}{{21}} \times \frac{7}{4} = \frac{{56}}{{84}} = \frac{2}{3}\,\)
c) \(\frac{5}{8}:\frac{{15}}{8} = \frac{5}{8} \times \frac{8}{{15}} = \frac{{40}}{{120}} = \frac{1}{3}\)
Video hướng dẫn giải
Tính (theo mẫu).

Phương pháp giải:
Thực hiện các phép chia theo ví dụ mẫu
Lời giải chi tiết:
a) \(3:\frac{5}{7} = \frac{{3 \times 7}}{5}{\text{ = }}\frac{{21}}{5}\)
b) \(\,4:\frac{1}{3} = \frac{{4 \times 3}}{1} = 12\)
c) \(\frac{5}{7}:3 = \frac{5}{{7 \times 3}} = \frac{5}{{21}}\,\)
Video hướng dẫn giải
Vào một buổi chiều, người ta đo được chiều dài cái bóng của ngọn tháp là $\frac{{99}}{4}$m. Biết chiều dài cái bóng của ngọn tháp gấp 2 lần chiều cao ngọn tháp. Tính chiều cao ngọn tháp.

Phương pháp giải:
Chiều cao ngọn tháp = chiều dài cái bóng : 2
Lời giải chi tiết:
Chiều cao ngọn tháp là:
$\frac{{99}}{4}:2 = \frac{{99}}{8}$ (m)
Đáp số: $\frac{{99}}{8}$ m
>> Xem chi tiết: Lý thuyết: Bài 64. Phép chia phân số - SGK Kết nối tri thức
Bài 64 trong sách giáo khoa Toán lớp 4 Kết nối tri thức giới thiệu về phép chia phân số, một khái niệm quan trọng trong chương trình học. Để hiểu rõ hơn về phép chia phân số, chúng ta cần nắm vững các khái niệm cơ bản về phân số, bao gồm tử số, mẫu số và cách so sánh phân số.
Phép chia phân số là phép toán ngược với phép nhân phân số. Để chia một phân số cho một phân số khác, ta thực hiện như sau:
Ví dụ: a : b = a x 1/b
Ví dụ 1: Tính 2/3 : 1/2
Giải:
Vậy, 2/3 : 1/2 = 4/3
Ví dụ 2: Tính 3/4 : 3/8
Giải:
Vậy, 3/4 : 3/8 = 2
Dưới đây là một số bài tập thực hành để các em học sinh có thể luyện tập và củng cố kiến thức về phép chia phân số:
Phép chia phân số có ứng dụng rất lớn trong cuộc sống hàng ngày. Ví dụ, khi chia một chiếc bánh pizza thành các phần bằng nhau, chúng ta đang thực hiện phép chia phân số. Ngoài ra, phép chia phân số còn được sử dụng trong các bài toán về tỷ lệ, phần trăm và các lĩnh vực khác.
Khi thực hiện phép chia phân số, cần lưu ý:
Hy vọng với những kiến thức và ví dụ minh họa trên, các em học sinh đã hiểu rõ hơn về phép chia phân số. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
| Phân số bị chia | Phân số chia | Kết quả |
|---|---|---|
| 1/2 | 1/4 | 2 |
| 2/5 | 3/10 | 4/3 |
| 4/7 | 2/3 | 6/7 |