Bài học Toán lớp 5 Bài 26 tập trung vào việc giới thiệu về hình thang và cách tính diện tích của hình thang. Đây là một kiến thức quan trọng trong chương trình học Toán lớp 5, giúp các em học sinh hiểu rõ hơn về các hình học cơ bản và ứng dụng vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập vận dụng đa dạng, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
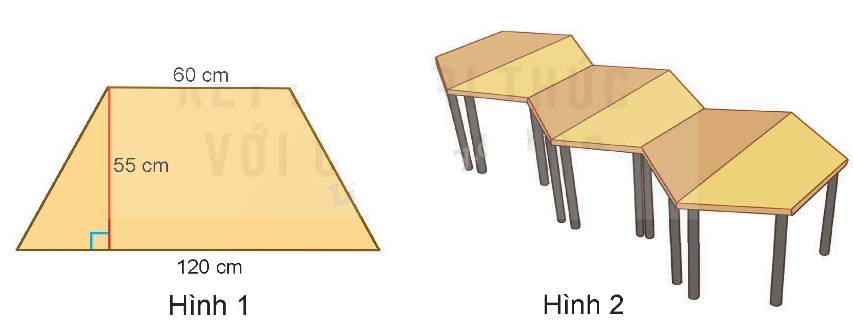
Trong các hình dưới đây, hình nào là hình thang? Tính diện tích hình thang biết: a) Độ dài hai đáy lần lượt là 4 cm và 6cm; chiều cao là 3 cm. Dùng 6 cái bàn giống nhau với mặt bàn hình thang có kích thước như hình 1 để ghép thành một bàn đa năng như hình 2.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 103 SGK Toán 5 Kết nối tri thức
Tính diện tích hình thang, biết:
a) Độ dài hai đáy lần lượt là 4 cm và 6cm; chiều cao là 3 cm.
b) Độ dài hai đáy lần lượt là 11 cm và 9 cm; chiều cao là 8 cm.
Phương pháp giải:
Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó:
S là diện tích;
a, b là độ dài các cạnh đáy;
h là chiều cao.
Lời giải chi tiết:
a) Diện tích hình thang là:
$\frac{{\left( {6 + 4} \right) \times 3}}{2} = 15\left( {c{m^2}} \right)$
b) Diện tích của hình thang là:
$\frac{{\left( {11 + 9} \right) \times 8}}{2} = 80\;\left( {c{m^2}} \right)$
Đáp số: a) 15 cm2
b) 80 cm2
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 104 SGK Toán 5 Kết nối tri thức
Chọn câu trả lời đúng.
Diện tích hình thang có độ dài hai đáy lần lượt là 25 cm và 15 cm; chiều cao 1 dm là:
A. 4 cm2
B. 2 cm2
C. 2 dm2
D. 4 dm2
Phương pháp giải:
Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó: S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
Lời giải chi tiết:
Đổi 1 dm = 10 cm
Diện tích hình thang là: $\frac{{\left( {25 + 15} \right) \times 10}}{2} = 200\;$(cm2)= 2 dm2
Chọn đáp án C.
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 99 SGK Toán 5 Kết nối tri thức
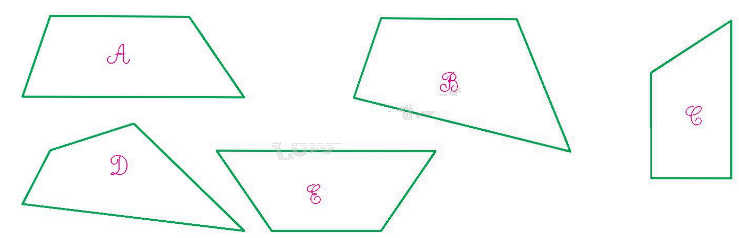
Trong các hình dưới đây, hình nào là hình thang?
Phương pháp giải:
Hình thang có một cặp cạnh đối diện song song.
Lời giải chi tiết:
Các hình là hình thang: Hình A, Hình C và hình E.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 101 SGK Toán 5 Kết nối tri thức
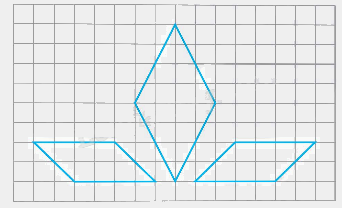
Vẽ hình (theo mẫu).
Phương pháp giải:
HS vẽ theo mẫu.
Lời giải chi tiết:
Học sinh tự thực hiện.
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 101 SGK Toán 5 Kết nối tri thức
a) Vẽ hình (theo mẫu).
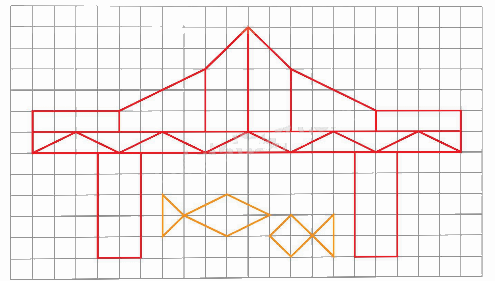
b) Tô màu trang trí hình em vừa vẽ được ở câu a.
Phương pháp giải:
HS vẽ theo mẫu.
Lời giải chi tiết:
Học sinh tự thực hiện
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 103 SGK Toán 5 Kết nối tri thức
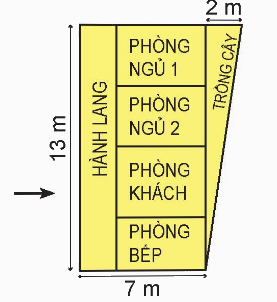
a) Hình bên là bản vẽ thiết kế một ngôi nhà trên mảnh đất có dạng hình thang vuông. Tính diện tích mảnh đất đó.
b) Với mảnh đất như vậy, hãy thiết kế lại các phòng theo ý thích của em.
Phương pháp giải:
- Tìm chiều dài mảnh đất
- Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó:
S là diện tích;
a, b là độ dài các cạnh đáy;
h là chiều cao.
Lời giải chi tiết:
a) Chiều dài mảnh đất là:
7 + 2 = 9 (m)
Diện tích mảnh đất đó là:
$\frac{{(9 + 7) \times 13}}{2} = 104$ (m2)
Đáp số: 104 m2
b) Học sinh tự thực hiện
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 103 SGK Toán 5 Kết nối tri thức
Dùng 6 cái bàn giống nhau với mặt bàn hình thang có kích thước như hình 1 để ghép thành một bàn đa năng như hình 2. Tính diện tích mặt bàn đa năng.
Phương pháp giải:
- Tìm diện tích mặt bàn hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Diện tích mặt bàn đa năng = diện tích hình thang x 6
Lời giải chi tiết:
Diện tích mặt bàn hình thang là:
$\frac{{\left( {120 + 60} \right) \times 55}}{2} = 4\;950\;\left( {c{m^2}} \right)$
Diện tích mặt bàn đa năng như hình 2 là:
4 950 x 6 = 29 700 (cm2)
Đáp số: 29 700 cm2
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 99 SGK Toán 5 Kết nối tri thức
a) Hình thang vuông.
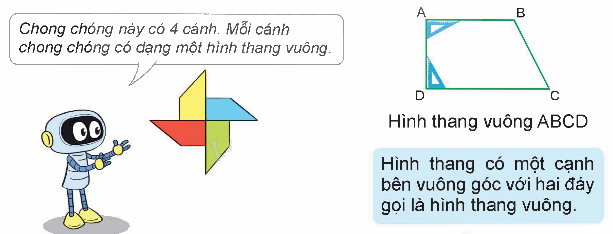
b) Sử dụng ê ke để kiểm tra xem mỗi hình thang bên có phải là hình thang vuông không.
Phương pháp giải:
Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.
Lời giải chi tiết:
Mỗi hình thang bên không phải là hình thang vuông.
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 100 SGK Toán 5 Kết nối tri thức
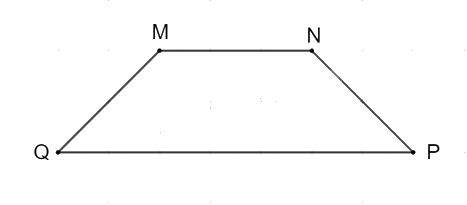
Vẽ hình thang MNPQ với MN và QP là hay đáy (trên giấy kẻ ô vuông).
Phương pháp giải:
- Vẽ đoạn thẳng MN.
- Vẽ đoạn thẳng QP song song với đoạn thẳng MN.
- Nối M với Q và N với P ta được hình thang MNPQ với hai đáy là MN và QP.
Lời giải chi tiết:
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 104 SGK Toán 5 Kết nối tri thức
Một mảnh đất dạng hình thang có độ dài hai đáy là 35 m và 15 m, chiều cao là 20 m. Tính số tiền mua cỏ để vừa đủ phủ kín mảnh đất đó, biết rằng mỗi mét vuông cỏ có giá tiền là 45 000 đồng.

Phương pháp giải:
- Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Số tiền mua cỏ = số tiền mỗi mét vuông cỏ x diện tích mảnh đất
Lời giải chi tiết:
Diện tích mảnh đất là:
$\frac{{\left( {35 + 15} \right) \times 20}}{2} = 500\;\left( {{m^2}} \right)$
Số tiền mua cỏ để vừa đủ phủ kín mảnh đất là:
45 000 x 500 = 22 500 000 (đồng)
Đáp số: 22 500 000 đồng.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 100 SGK Toán 5 Kết nối tri thức
Cho hình vẽ:
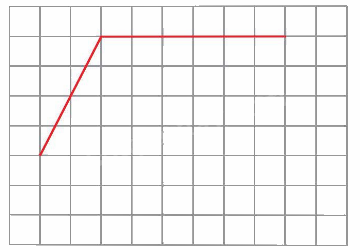
Thực hiện yêu cầu vẽ thêm hai đoạn thẳng vào hình vẽ để được một hình thang, Mai và Việt đã làm như sau:
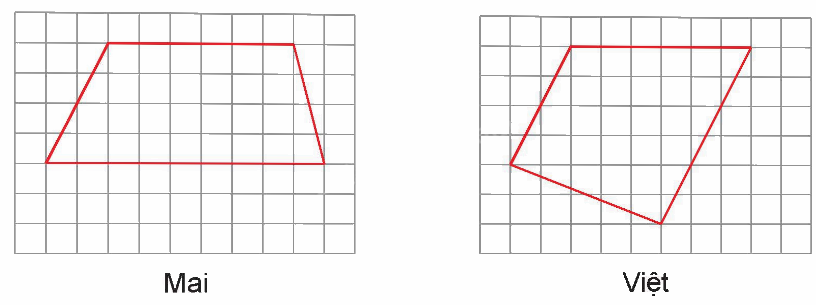
Hỏi bạn nào thực hiện đúng yêu cầu?
Phương pháp giải:
Hình thang có một cặp cạnh đối diện song song.
Lời giải chi tiết:
Cả hai bạn Mai và Việt đều làm đúng yêu cầu vì hai hình trên đều có 1 cặp đường thẳng song song.
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 104 SGK Toán 5 Kết nối tri thức
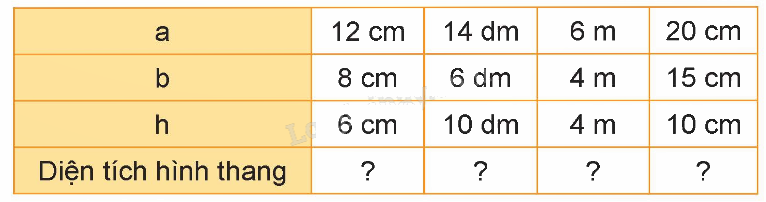
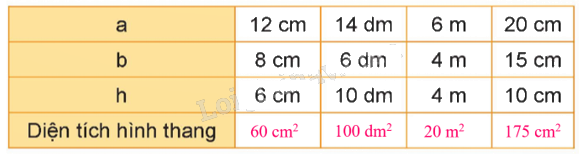
Tính diện tích hình thang có độ dài hay đáy lần lượt là a và b; chiều cao là h được cho như bảng dưới đây:
Phương pháp giải:
Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó: S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
Lời giải chi tiết:
Diện tích hình thang có a = 12 cm, b = 8 cm, h = 6 cm là: $\frac{{(12 + 8) \times 6}}{2} = 60$ (cm2)
Diện tích hình thang có a = 14 dm, b = 6 dm, h = 10 dm là: $\frac{{(14 + 6) \times 10}}{2} = 100$ (dm2)
Diện tích hình thang có a = 6 m, b = 4 m, h = 4 m là: $\frac{{(6 + 4) \times 4}}{2} = 20$ (m2)
Diện tích hình thang có a = 20 cm, b = 15 cm, h = 10 cm là: $\frac{{(20 + 15) \times 10}}{2} = 175$ (cm2)
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 104 SGK Toán 5 Kết nối tri thức
Tính diện tích con thuyền như hình dưới đây, biết rằng mỗi ô vuông có cạnh dài 1 cm.
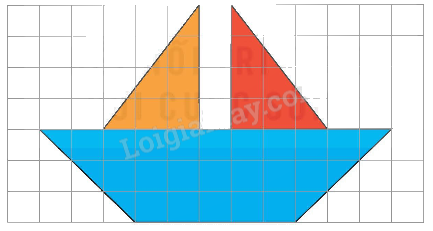
Phương pháp giải:
- Tính diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
- Diện tích con thuyền = Diện tích hình thang + diện tích hình tam giác x 2
Lời giải chi tiết:
Diện tích hình tam giác vuông có độ dài hai cạnh góc vuông là 3 cm và 4 cm là:
$\frac{{3 \times 4}}{2} = 6\left( {c{m^2}} \right)$
Diện tích hình thang có chiều dài 11 cm, chiều rộng 5 cm, chiều cao 3 cm là:
\[\frac{{\left( {11 + 5} \right) \times 3}}{2} = 24\left( {c{m^2}} \right)\]
Diện tích con thuyền là:
6 x 2 + 24 = 36 (cm2)
Đáp số: 36 cm2
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 99 SGK Toán 5 Kết nối tri thức
Dưới đây là một số hình ảnh thực tế có dạng hình thang. Em hãy tìm thêm một số hình ảnh thực tế có dạng hình thang.
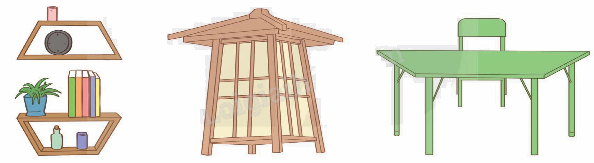
Phương pháp giải:
Em tìm thêm một số hình ảnh thực tế có dạng hình thang.
Lời giải chi tiết:
Một số hình ảnh thực tế có dạng hình thang: cái thang, túi xách, ...


Video hướng dẫn giải
Trả lời câu hỏi 1 trang 99 SGK Toán 5 Kết nối tri thức
Trong các hình dưới đây, hình nào là hình thang?
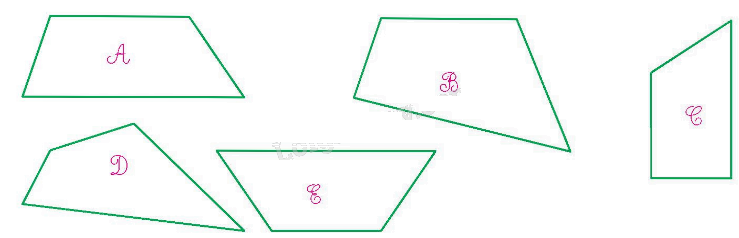
Phương pháp giải:
Hình thang có một cặp cạnh đối diện song song.
Lời giải chi tiết:
Các hình là hình thang: Hình A, Hình C và hình E.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 99 SGK Toán 5 Kết nối tri thức
Dưới đây là một số hình ảnh thực tế có dạng hình thang. Em hãy tìm thêm một số hình ảnh thực tế có dạng hình thang.
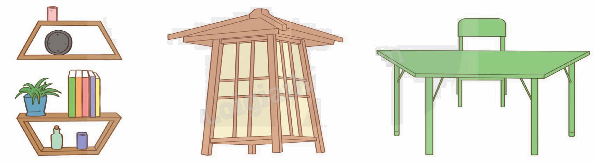
Phương pháp giải:
Em tìm thêm một số hình ảnh thực tế có dạng hình thang.
Lời giải chi tiết:
Một số hình ảnh thực tế có dạng hình thang: cái thang, túi xách, ...


Video hướng dẫn giải
Trả lời câu hỏi 3 trang 99 SGK Toán 5 Kết nối tri thức
a) Hình thang vuông.
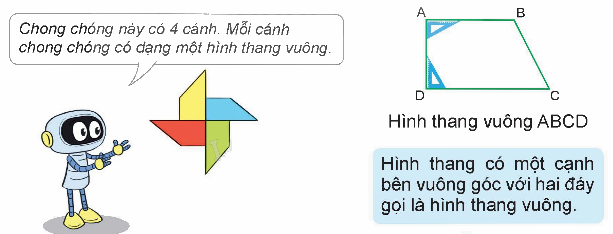
b) Sử dụng ê ke để kiểm tra xem mỗi hình thang bên có phải là hình thang vuông không.
Phương pháp giải:
Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.
Lời giải chi tiết:
Mỗi hình thang bên không phải là hình thang vuông.
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 100 SGK Toán 5 Kết nối tri thức
Vẽ hình thang MNPQ với MN và QP là hay đáy (trên giấy kẻ ô vuông).
Phương pháp giải:
- Vẽ đoạn thẳng MN.
- Vẽ đoạn thẳng QP song song với đoạn thẳng MN.
- Nối M với Q và N với P ta được hình thang MNPQ với hai đáy là MN và QP.
Lời giải chi tiết:
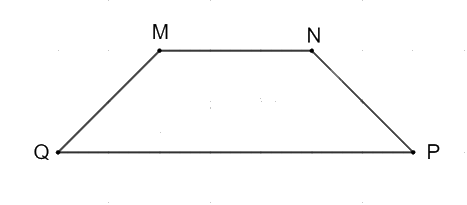
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 100 SGK Toán 5 Kết nối tri thức
Cho hình vẽ:
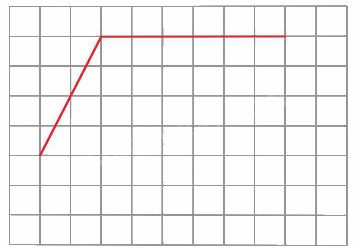
Thực hiện yêu cầu vẽ thêm hai đoạn thẳng vào hình vẽ để được một hình thang, Mai và Việt đã làm như sau:
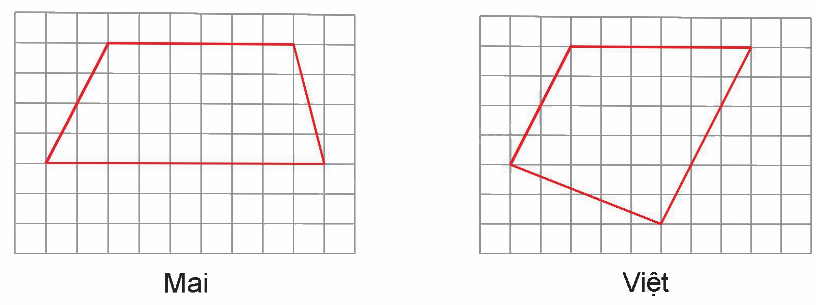
Hỏi bạn nào thực hiện đúng yêu cầu?
Phương pháp giải:
Hình thang có một cặp cạnh đối diện song song.
Lời giải chi tiết:
Cả hai bạn Mai và Việt đều làm đúng yêu cầu vì hai hình trên đều có 1 cặp đường thẳng song song.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 101 SGK Toán 5 Kết nối tri thức
Vẽ hình (theo mẫu).
Phương pháp giải:
HS vẽ theo mẫu.
Lời giải chi tiết:
Học sinh tự thực hiện.
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 101 SGK Toán 5 Kết nối tri thức
a) Vẽ hình (theo mẫu).
b) Tô màu trang trí hình em vừa vẽ được ở câu a.
Phương pháp giải:
HS vẽ theo mẫu.
Lời giải chi tiết:
Học sinh tự thực hiện
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 103 SGK Toán 5 Kết nối tri thức
Tính diện tích hình thang, biết:
a) Độ dài hai đáy lần lượt là 4 cm và 6cm; chiều cao là 3 cm.
b) Độ dài hai đáy lần lượt là 11 cm và 9 cm; chiều cao là 8 cm.
Phương pháp giải:
Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó:
S là diện tích;
a, b là độ dài các cạnh đáy;
h là chiều cao.
Lời giải chi tiết:
a) Diện tích hình thang là:
$\frac{{\left( {6 + 4} \right) \times 3}}{2} = 15\left( {c{m^2}} \right)$
b) Diện tích của hình thang là:
$\frac{{\left( {11 + 9} \right) \times 8}}{2} = 80\;\left( {c{m^2}} \right)$
Đáp số: a) 15 cm2
b) 80 cm2
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 103 SGK Toán 5 Kết nối tri thức
Dùng 6 cái bàn giống nhau với mặt bàn hình thang có kích thước như hình 1 để ghép thành một bàn đa năng như hình 2. Tính diện tích mặt bàn đa năng.
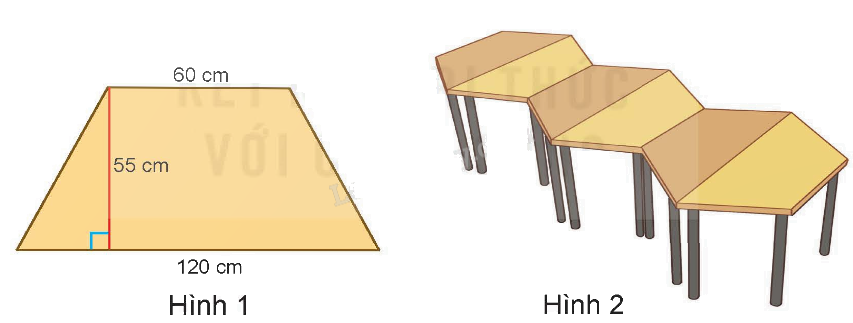
Phương pháp giải:
- Tìm diện tích mặt bàn hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Diện tích mặt bàn đa năng = diện tích hình thang x 6
Lời giải chi tiết:
Diện tích mặt bàn hình thang là:
$\frac{{\left( {120 + 60} \right) \times 55}}{2} = 4\;950\;\left( {c{m^2}} \right)$
Diện tích mặt bàn đa năng như hình 2 là:
4 950 x 6 = 29 700 (cm2)
Đáp số: 29 700 cm2
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 103 SGK Toán 5 Kết nối tri thức
a) Hình bên là bản vẽ thiết kế một ngôi nhà trên mảnh đất có dạng hình thang vuông. Tính diện tích mảnh đất đó.
b) Với mảnh đất như vậy, hãy thiết kế lại các phòng theo ý thích của em.
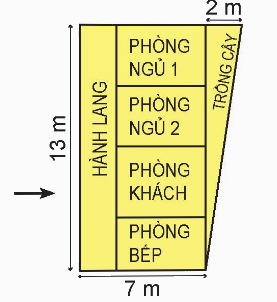
Phương pháp giải:
- Tìm chiều dài mảnh đất
- Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó:
S là diện tích;
a, b là độ dài các cạnh đáy;
h là chiều cao.
Lời giải chi tiết:
a) Chiều dài mảnh đất là:
7 + 2 = 9 (m)
Diện tích mảnh đất đó là:
$\frac{{(9 + 7) \times 13}}{2} = 104$ (m2)
Đáp số: 104 m2
b) Học sinh tự thực hiện
Video hướng dẫn giải
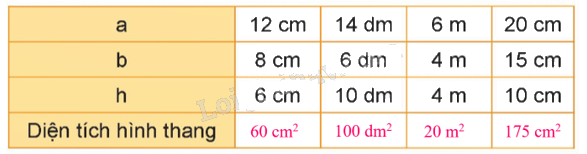
Trả lời câu hỏi 1 trang 104 SGK Toán 5 Kết nối tri thức
Tính diện tích hình thang có độ dài hay đáy lần lượt là a và b; chiều cao là h được cho như bảng dưới đây:
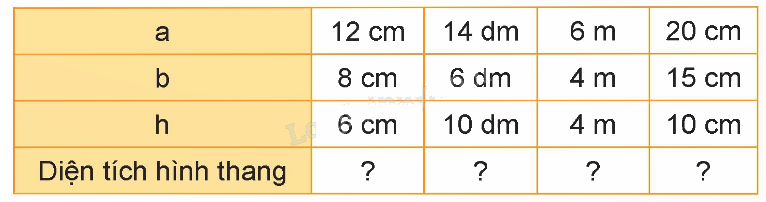
Phương pháp giải:
Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó: S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
Lời giải chi tiết:
Diện tích hình thang có a = 12 cm, b = 8 cm, h = 6 cm là: $\frac{{(12 + 8) \times 6}}{2} = 60$ (cm2)
Diện tích hình thang có a = 14 dm, b = 6 dm, h = 10 dm là: $\frac{{(14 + 6) \times 10}}{2} = 100$ (dm2)
Diện tích hình thang có a = 6 m, b = 4 m, h = 4 m là: $\frac{{(6 + 4) \times 4}}{2} = 20$ (m2)
Diện tích hình thang có a = 20 cm, b = 15 cm, h = 10 cm là: $\frac{{(20 + 15) \times 10}}{2} = 175$ (cm2)
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 104 SGK Toán 5 Kết nối tri thức
Chọn câu trả lời đúng.
Diện tích hình thang có độ dài hai đáy lần lượt là 25 cm và 15 cm; chiều cao 1 dm là:
A. 4 cm2
B. 2 cm2
C. 2 dm2
D. 4 dm2
Phương pháp giải:
Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó: S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
Lời giải chi tiết:
Đổi 1 dm = 10 cm
Diện tích hình thang là: $\frac{{\left( {25 + 15} \right) \times 10}}{2} = 200\;$(cm2)= 2 dm2
Chọn đáp án C.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 104 SGK Toán 5 Kết nối tri thức
Tính diện tích con thuyền như hình dưới đây, biết rằng mỗi ô vuông có cạnh dài 1 cm.
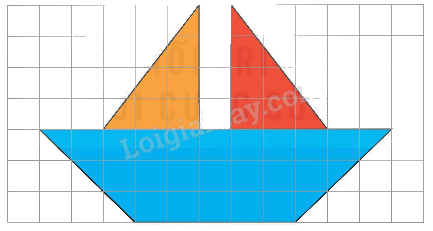
Phương pháp giải:
- Tính diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
- Diện tích con thuyền = Diện tích hình thang + diện tích hình tam giác x 2
Lời giải chi tiết:
Diện tích hình tam giác vuông có độ dài hai cạnh góc vuông là 3 cm và 4 cm là:
$\frac{{3 \times 4}}{2} = 6\left( {c{m^2}} \right)$
Diện tích hình thang có chiều dài 11 cm, chiều rộng 5 cm, chiều cao 3 cm là:
\[\frac{{\left( {11 + 5} \right) \times 3}}{2} = 24\left( {c{m^2}} \right)\]
Diện tích con thuyền là:
6 x 2 + 24 = 36 (cm2)
Đáp số: 36 cm2
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 104 SGK Toán 5 Kết nối tri thức
Một mảnh đất dạng hình thang có độ dài hai đáy là 35 m và 15 m, chiều cao là 20 m. Tính số tiền mua cỏ để vừa đủ phủ kín mảnh đất đó, biết rằng mỗi mét vuông cỏ có giá tiền là 45 000 đồng.

Phương pháp giải:
- Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Số tiền mua cỏ = số tiền mỗi mét vuông cỏ x diện tích mảnh đất
Lời giải chi tiết:
Diện tích mảnh đất là:
$\frac{{\left( {35 + 15} \right) \times 20}}{2} = 500\;\left( {{m^2}} \right)$
Số tiền mua cỏ để vừa đủ phủ kín mảnh đất là:
45 000 x 500 = 22 500 000 (đồng)
Đáp số: 22 500 000 đồng.
Bài 26 Toán lớp 5 thuộc chương trình kết nối tri thức, giới thiệu về hình thang và công thức tính diện tích hình thang. Dưới đây là nội dung chi tiết bài học, cùng với các ví dụ minh họa và bài tập vận dụng để giúp các em học sinh hiểu rõ hơn về kiến thức này.
Định nghĩa: Hình thang là hình tứ giác có hai cạnh đối song song. Hai cạnh song song đó gọi là hai đáy của hình thang, cạnh còn lại gọi là hai cạnh bên.
Ví dụ: Một mảnh đất hình thang có chiều dài hai đáy là 10m và 6m, chiều cao là 5m.
Công thức: Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.
S = (a + b) x h / 2
Trong đó:
Ví dụ 1: Một hình thang có độ dài hai đáy lần lượt là 8cm và 12cm, chiều cao là 5cm. Tính diện tích hình thang đó.
Giải:
Diện tích hình thang là: (8 + 12) x 5 / 2 = 50 cm2
Ví dụ 2: Một hình thang có diện tích là 60cm2, chiều cao là 4cm, đáy lớn là 15cm. Tính độ dài đáy nhỏ.
Giải:
Tổng độ dài hai đáy là: 60 x 2 / 4 = 30cm
Đáy nhỏ là: 30 - 15 = 15cm
Ngoài công thức tính diện tích hình thang, các em học sinh cũng cần nắm vững các khái niệm liên quan như chiều cao, đáy lớn, đáy nhỏ. Việc hiểu rõ các khái niệm này sẽ giúp các em giải quyết các bài toán một cách dễ dàng và chính xác hơn.
Để củng cố kiến thức về hình thang và cách tính diện tích hình thang, các em có thể luyện tập thêm các bài tập trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài giảng online trên giaitoan.edu.vn để học hỏi thêm kinh nghiệm và phương pháp giải toán.
Hy vọng với bài viết này, các em học sinh đã nắm vững kiến thức về Toán lớp 5 Bài 26: Hình thang, Diện tích hình thang. Chúc các em học tập tốt!