Bài học Toán lớp 5 Bài 6: Cộng, trừ hai phân số khác mẫu số thuộc chương trình SGK kết nối tri thức là một trong những kiến thức quan trọng giúp các em học sinh nắm vững các phép toán với phân số. Bài học này tập trung vào việc tìm hiểu cách quy đồng mẫu số để thực hiện phép cộng và trừ phân số một cách chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cùng với các bài tập luyện tập đa dạng để giúp các em học sinh hiểu sâu và vận dụng kiến thức một cách hiệu quả.
Có hai vòi nước cùng chảy vào một bể. Vòi thứ nhất chảy được 1/2 bể, Chọn dấu “+”, dấu “ –” thích hợp thay cho dấu “?”Để chia đều 5 chiếc bánh cho 6 người, hai bạn Nam và Rô-bốt đã đề xuất cách làm như hình
Video hướng dẫn giải
Trả lời câu hỏi 2 phần Hoạt động trang 21 SGK Toán 5 Kết nối tri thức
Có hai vòi nước cùng chảy vào một bể. Vòi thứ nhất chảy được $\frac{1}{2}$ bể, vòi thứ hai chảy được $\frac{2}{5}$ bể. Hỏi cả hai vòi chảy được bao nhiêu phần bể nước?
Phương pháp giải:
Hai vòi chảy được số phần bể nước = số phần bể vòi thứ nhất chảy được + số phần bể vòi thứ hai chảy được.
Lời giải chi tiết:
Tóm tắt
Vòi thứ nhất: $\frac{1}{2}$ bể
Vòi thứ hai: $\frac{2}{5}$ bể
Cả hai vòi: ? bể
Bài giải
Hai vòi chảy được số phần bể nước là:
$\frac{1}{2} + \frac{2}{5} = \frac{9}{{10}}$ (bể)
Đáp số: $\frac{9}{{10}}$ bể nước
>> Xem chi tiết: Lý thuyết Cộng, trừ hai phân số khác mẫu số- Toán 5 Kết nối tri thức
Video hướng dẫn giải
Trả lời câu hỏi 1 phần Hoạt động trang 21 SGK Toán 5 Kết nối tri thức
Tính.
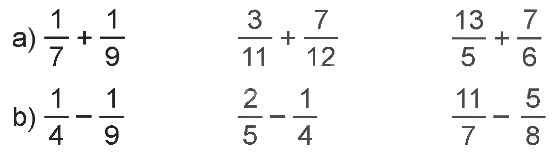
Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $\frac{1}{7} + \frac{1}{9} = \frac{9}{{63}} + \frac{7}{{63}} = \frac{{16}}{{63}}$
$\frac{3}{{11}} + \frac{7}{{12}} = \frac{{36}}{{132}} + \frac{{77}}{{132}} = \frac{{113}}{{132}}$
$\;\frac{{13}}{5} + \frac{7}{6} = \frac{{78}}{{30}} + \frac{{35}}{{30}} = \frac{{113}}{{30}}$
b) $\frac{1}{4} - \frac{1}{9} = \frac{9}{{36}} - \frac{4}{{36}} = \frac{5}{{36}}$
$\frac{2}{5} - \frac{1}{4} = \frac{8}{{20}} - \frac{5}{{20}} = \frac{3}{{20}}$
$\frac{{11}}{7} - \frac{5}{8} = \frac{{88}}{{56}} - \frac{{35}}{{56}} = \frac{{53}}{{56}}$
Video hướng dẫn giải
Trả lời câu hỏi 1 phần Luyện tập trang 21 SGK Toán 5 Kết nối tri thức
Tính.

Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $\frac{6}{{11}} + \frac{1}{2} = \frac{{12}}{{22}} + \frac{{11}}{{22}} = \frac{{23}}{{22}}$
b) $\frac{3}{{10}} + \frac{5}{{21}} = \frac{{63}}{{210}} + \frac{{50}}{{210}} = \frac{{113}}{{210}}$
c) $\frac{{11}}{4} - \frac{7}{5} = \frac{{55}}{{20}} - \frac{{28}}{{20}} = \frac{{27}}{{20}}$
d) $\frac{{20}}{{18}} - \frac{2}{5} = \frac{{10}}{9} - \frac{2}{5} = \frac{{50}}{{45}} - \frac{{18}}{{45}} = \frac{{32}}{{45}}$
Video hướng dẫn giải
Trả lời câu hỏi 3 phần Luyện tập trang 22 SGK Toán 5 Kết nối tri thức
Tính.

Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $7 + \frac{1}{5} = \frac{{35}}{5} + \frac{1}{5} = \frac{{36}}{5}$ b) $\frac{{14}}{5} + 1 = \frac{{14}}{5} + \frac{5}{5} = \frac{{19}}{5}$
c) $3 - \frac{{11}}{8} = \frac{{24}}{8} - \frac{{11}}{8} = \frac{{13}}{8}$
d) $\frac{{31}}{{10}} - 2 = \frac{{31}}{{10}} - \frac{{20}}{{10}} = \frac{{11}}{{10}}$
Video hướng dẫn giải
Trả lời câu hỏi 2 phần Luyện tập trang 21 SGK Toán 5 Kết nối tri thức
Chọn dấu “+”, dấu “ –” thích hợp thay cho dấu “?”.
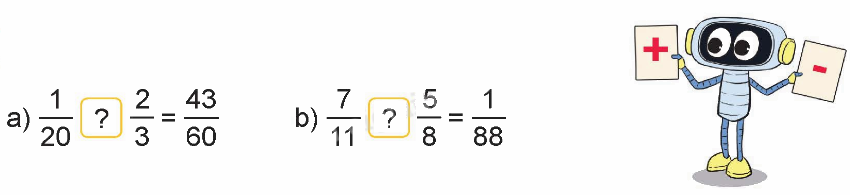
Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
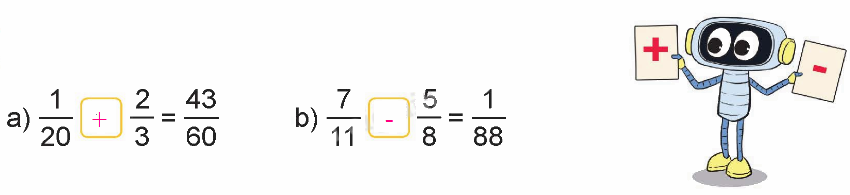
Video hướng dẫn giải
Trả lời câu hỏi 4 phần Luyện tập trang 22 SGK Toán 5 Kết nối tri thức
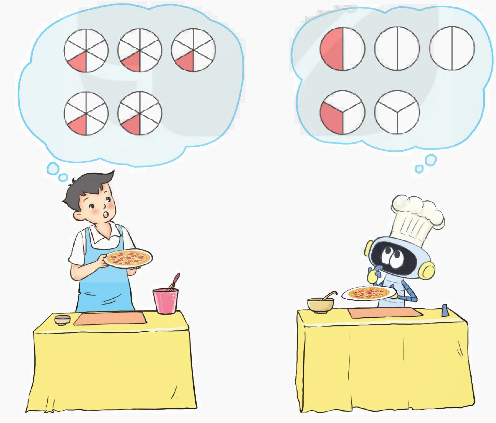
Để chia đều 5 chiếc bánh cho 6 người, hai bạn Nam và Rô-bốt đã đề xuất cách làm như hình dưới đây (phần bánh của mỗi người thể hiện bằng các phần tô màu đỏ).
a) Em hãy mô tả cách chia bánh của mỗi bạn.
b) Em hãy giải thích vì sao với cách chia bánh của Rô-bốt thì mỗi bạn được $\frac{5}{6}$ cái bánh.
Phương pháp giải:
Quan sát hình vẽ để mô tả cách chia bánh của mỗi bạn
Lời giải chi tiết:
a) Bạn Nam chia mỗi chiếc bánh thành 6 phần bằng nhau. Mỗi người được nhận 1 phần trên mỗi chiếc bánh đó.
Bạn Rô-bốt chia chiếc bánh thứ nhất thành 2 phần, chiếc bánh thứ hai thành 3 phần. Mỗi người được nhận 1 phần trên mỗi chiếc bánh đó.
b) Ta có $\frac{1}{2} + \frac{1}{3} = \frac{5}{6}$
Vậy với cách chia bánh của Rô-bốt thì mỗi bạn được $\frac{5}{6}$ cái bánh.
Video hướng dẫn giải
Trả lời câu hỏi 1 phần Hoạt động trang 21 SGK Toán 5 Kết nối tri thức
Tính.
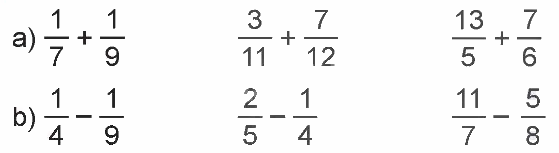
Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $\frac{1}{7} + \frac{1}{9} = \frac{9}{{63}} + \frac{7}{{63}} = \frac{{16}}{{63}}$
$\frac{3}{{11}} + \frac{7}{{12}} = \frac{{36}}{{132}} + \frac{{77}}{{132}} = \frac{{113}}{{132}}$
$\;\frac{{13}}{5} + \frac{7}{6} = \frac{{78}}{{30}} + \frac{{35}}{{30}} = \frac{{113}}{{30}}$
b) $\frac{1}{4} - \frac{1}{9} = \frac{9}{{36}} - \frac{4}{{36}} = \frac{5}{{36}}$
$\frac{2}{5} - \frac{1}{4} = \frac{8}{{20}} - \frac{5}{{20}} = \frac{3}{{20}}$
$\frac{{11}}{7} - \frac{5}{8} = \frac{{88}}{{56}} - \frac{{35}}{{56}} = \frac{{53}}{{56}}$
Video hướng dẫn giải
Trả lời câu hỏi 2 phần Hoạt động trang 21 SGK Toán 5 Kết nối tri thức
Có hai vòi nước cùng chảy vào một bể. Vòi thứ nhất chảy được $\frac{1}{2}$ bể, vòi thứ hai chảy được $\frac{2}{5}$ bể. Hỏi cả hai vòi chảy được bao nhiêu phần bể nước?
Phương pháp giải:
Hai vòi chảy được số phần bể nước = số phần bể vòi thứ nhất chảy được + số phần bể vòi thứ hai chảy được.
Lời giải chi tiết:
Tóm tắt
Vòi thứ nhất: $\frac{1}{2}$ bể
Vòi thứ hai: $\frac{2}{5}$ bể
Cả hai vòi: ? bể
Bài giải
Hai vòi chảy được số phần bể nước là:
$\frac{1}{2} + \frac{2}{5} = \frac{9}{{10}}$ (bể)
Đáp số: $\frac{9}{{10}}$ bể nước
Video hướng dẫn giải
Trả lời câu hỏi 1 phần Luyện tập trang 21 SGK Toán 5 Kết nối tri thức
Tính.

Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $\frac{6}{{11}} + \frac{1}{2} = \frac{{12}}{{22}} + \frac{{11}}{{22}} = \frac{{23}}{{22}}$
b) $\frac{3}{{10}} + \frac{5}{{21}} = \frac{{63}}{{210}} + \frac{{50}}{{210}} = \frac{{113}}{{210}}$
c) $\frac{{11}}{4} - \frac{7}{5} = \frac{{55}}{{20}} - \frac{{28}}{{20}} = \frac{{27}}{{20}}$
d) $\frac{{20}}{{18}} - \frac{2}{5} = \frac{{10}}{9} - \frac{2}{5} = \frac{{50}}{{45}} - \frac{{18}}{{45}} = \frac{{32}}{{45}}$
Video hướng dẫn giải
Trả lời câu hỏi 2 phần Luyện tập trang 21 SGK Toán 5 Kết nối tri thức
Chọn dấu “+”, dấu “ –” thích hợp thay cho dấu “?”.
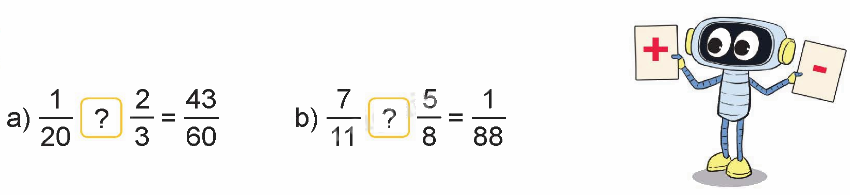
Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
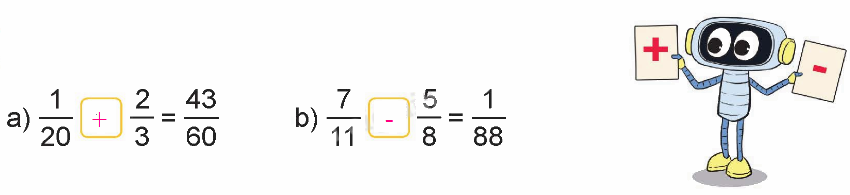
Video hướng dẫn giải
Trả lời câu hỏi 3 phần Luyện tập trang 22 SGK Toán 5 Kết nối tri thức
Tính.

Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $7 + \frac{1}{5} = \frac{{35}}{5} + \frac{1}{5} = \frac{{36}}{5}$ b) $\frac{{14}}{5} + 1 = \frac{{14}}{5} + \frac{5}{5} = \frac{{19}}{5}$
c) $3 - \frac{{11}}{8} = \frac{{24}}{8} - \frac{{11}}{8} = \frac{{13}}{8}$
d) $\frac{{31}}{{10}} - 2 = \frac{{31}}{{10}} - \frac{{20}}{{10}} = \frac{{11}}{{10}}$
Video hướng dẫn giải
Trả lời câu hỏi 4 phần Luyện tập trang 22 SGK Toán 5 Kết nối tri thức
Để chia đều 5 chiếc bánh cho 6 người, hai bạn Nam và Rô-bốt đã đề xuất cách làm như hình dưới đây (phần bánh của mỗi người thể hiện bằng các phần tô màu đỏ).
a) Em hãy mô tả cách chia bánh của mỗi bạn.
b) Em hãy giải thích vì sao với cách chia bánh của Rô-bốt thì mỗi bạn được $\frac{5}{6}$ cái bánh.
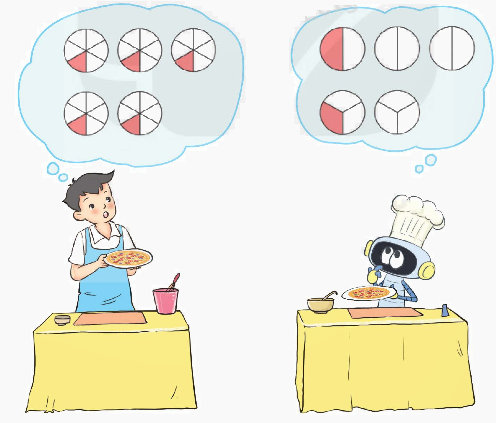
Phương pháp giải:
Quan sát hình vẽ để mô tả cách chia bánh của mỗi bạn
Lời giải chi tiết:
a) Bạn Nam chia mỗi chiếc bánh thành 6 phần bằng nhau. Mỗi người được nhận 1 phần trên mỗi chiếc bánh đó.
Bạn Rô-bốt chia chiếc bánh thứ nhất thành 2 phần, chiếc bánh thứ hai thành 3 phần. Mỗi người được nhận 1 phần trên mỗi chiếc bánh đó.
b) Ta có $\frac{1}{2} + \frac{1}{3} = \frac{5}{6}$
Vậy với cách chia bánh của Rô-bốt thì mỗi bạn được $\frac{5}{6}$ cái bánh.
>> Xem chi tiết: Lý thuyết Cộng, trừ hai phân số khác mẫu số- Toán 5 Kết nối tri thức
Bài 6 trong chương trình Toán lớp 5, sách Kết nối tri thức, tập trung vào việc giúp học sinh nắm vững phương pháp cộng và trừ hai phân số khi chúng có mẫu số khác nhau. Đây là một kỹ năng toán học cơ bản nhưng vô cùng quan trọng, là nền tảng cho các phép toán phức tạp hơn về phân số trong các lớp học tiếp theo.
Trước khi đi vào phần cộng trừ, chúng ta cần ôn lại khái niệm về phân số. Một phân số được biểu diễn dưới dạng a/b, trong đó a là tử số và b là mẫu số. Mẫu số cho biết một đơn vị được chia thành bao nhiêu phần bằng nhau, còn tử số cho biết ta lấy bao nhiêu phần trong số đó.
Khi cộng hoặc trừ hai phân số, chúng ta cần đảm bảo rằng chúng có cùng mẫu số. Mẫu số chung là một số mà cả hai mẫu số đều chia hết cho nó. Việc tìm mẫu số chung là bước quan trọng nhất trong quá trình cộng trừ phân số.
Có nhiều cách để quy đồng mẫu số, nhưng phương pháp phổ biến nhất là tìm bội chung nhỏ nhất (BCNN) của hai mẫu số. BCNN là số nhỏ nhất mà cả hai mẫu số đều chia hết cho nó.
Ví dụ: Để quy đồng mẫu số cho hai phân số 1/2 và 1/3, ta tìm BCNN của 2 và 3, đó là 6. Sau đó, ta biến đổi hai phân số thành:
Bây giờ, cả hai phân số đều có cùng mẫu số là 6, và ta có thể thực hiện phép cộng hoặc trừ.
Sau khi đã quy đồng mẫu số, việc cộng hai phân số trở nên đơn giản. Ta cộng hai tử số với nhau và giữ nguyên mẫu số chung.
Ví dụ: 3/6 + 2/6 = (3 + 2) / 6 = 5/6
Tương tự như phép cộng, ta trừ hai tử số với nhau và giữ nguyên mẫu số chung sau khi đã quy đồng.
Ví dụ: 5/6 - 2/6 = (5 - 2) / 6 = 3/6 = 1/2 (rút gọn)
Dưới đây là một số bài tập để các em luyện tập:
Hướng dẫn giải:
Đối với mỗi bài tập, các em cần thực hiện các bước sau:
Khi quy đồng mẫu số, các em cần đảm bảo rằng mẫu số chung là BCNN của hai mẫu số ban đầu. Điều này giúp cho việc tính toán trở nên dễ dàng và chính xác hơn.
Ngoài ra, sau khi thực hiện phép cộng hoặc trừ, các em nên kiểm tra xem phân số kết quả có thể rút gọn được hay không. Việc rút gọn phân số giúp cho kết quả trở nên đơn giản và dễ hiểu hơn.
Phép cộng và trừ phân số có rất nhiều ứng dụng trong thực tế. Ví dụ, khi nấu ăn, chúng ta thường cần đo lường các nguyên liệu bằng phân số. Khi tính toán diện tích hoặc thể tích, chúng ta cũng có thể sử dụng phép cộng và trừ phân số.
Hy vọng rằng bài học này đã giúp các em hiểu rõ hơn về cách cộng và trừ hai phân số khác mẫu số. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập toán học!
| Phân số 1 | Phân số 2 | Kết quả |
|---|---|---|
| 1/2 | 1/3 | 5/6 |
| 2/5 | 1/4 | 13/20 |