Dạng toán này là một phần quan trọng trong chương trình Toán nâng cao lớp 5, giúp học sinh rèn luyện kỹ năng giải quyết các bài toán thực tế liên quan đến chuyển động. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài tập đa dạng, từ cơ bản đến nâng cao, cùng với lời giải chi tiết và phương pháp giải hiệu quả.
Học sinh sẽ được làm quen với các khái niệm về vận tốc, thời gian, quãng đường và cách áp dụng chúng để giải quyết các bài toán một cách chính xác và nhanh chóng.
Một người đi xe máy từ A đến B mất 3 giờ. Lúc trở về do ngược gió mỗi giờ người ấy đi chậm hơn 10km so với lúc đi nên thời gian lúc về lâu hơn 1 giờ. Hằng ngày, Anh đi xe đạp từ nhà đến trường mất 20 phút. Sáng nay, do có việc bận, Anh xuất phát chậm mất 4 phút so với mọi ngày
Phương pháp giải 1. Các đại lượng thường gặp trong chuyển động đều: - Quãng đường, kí hiệu là s - Thời gian, kí hiệu là t - Vận tốc, kí hiệu là v 2. Những công thức thường dùng trong tính toán: - Công thức tính quãng đường: s = v x t - Công thức tính vận tốc: v = s : t - Công thức tính thời gian: t = s : v 3. Chú ý: - Với cùng một vận tốc thì quãng đường tỉ lệ thuận với thời gian. - Trong cùng một thời gian thì quãng đường tỉ lệ thuận với vận tốc. - Trên cùng một quãng đường thì vận tốc tỉ lệ nghịch với thời gian. |
Ví dụ 1:Một người đi xe máy từ A đến B mất 3 giờ. Lúc trở về do ngược gió mỗi giờ người ấy đi chậm hơn 10km so với lúc đi nên thời gian lúc về lâu hơn 1 giờ. Tính quãng đường AB?
Giải
Thời gian người ấy đi về hết:
3 + 1 = 4 (giờ).
Trên cùng quãng đường, thời gian và vận tốc là hai đại lượng tỉ lệ nghịch với nhau.
$\frac{{{v_1}}}{{{v_2}}} = \frac{{{t_2}}}{{{t_1}}} = \frac{4}{3}$
Ta có sơ đồ:
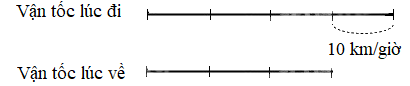
Vận tốc lúc đi là:
10 : ( 4 – 3) x 4 = 40 (km/giờ)
Quãng đường AB là
40 x 3 = 120 (km).
Đáp số: 120 km.
Ví dụ 2:Một ô tô dự kiến đi từ A đến B với vận tốc 45km/giờ thì đến B lúc 12 giờ trưa. Nhưng do trời trở gió nên mỗi giờ xe chỉ đi được 35km/giờ và đến B chậm 40 phút so với dự kiến. Tính quãng đường từ A đến B.
Giải
Trên cùng một quãng đường, vận tốc tỉ lệ nghịch với thời gian nên ta có
$\frac{{{v_1}}}{{{v_2}}} = \frac{{{t_2}}}{{{t_1}}}$ hay $\frac{{45}}{{35}} = \frac{9}{7} = \frac{{{t_2}}}{{{t_1}}}$
Vì thực tế xe đến chậm hơn dự định 40 phút nên t2 – t1 = 40

Thời gian thực tế ô tô đi hết quãng đường AB là
t2 = 40 : (9 – 7) x 9 = 180 (phút)
Đổi 180 phút = 3 giờ
Quãng đường AB dài là
35 x 3 = 105 (km)
Đáp số: 105 km
Ví dụ 3: Hằng ngày, Anh đi xe đạp từ nhà đến trường mất 20 phút. Sáng nay, do có việc bận, Anh xuất phát chậm mất 4 phút so với mọi ngày. Để đến trường đúng giờ, Anh tính mỗi phút phải đi nhanh hơn 50m so với mọi ngày. Hỏi quãng đường từ nhà Anh đến trường dài bao nhiêu ki-lô-mét?
Giải
Thời gian sáng nay Anh đi từ nhà đến trường là:
20 – 4 = 16 (phút)
Tỉ số giữa thời gian Anh đi hằng ngày và thời gian sáng nay Anh đi là
$20:16 = \frac{5}{4}$
Do thời gian và vận tốc Anh đi từ nhà đến trường là hai đại lượng tỉ lệ nghịch nên tỉ số giữa vận tốc hằng ngày và vận tốc sáng nay Anh đi bằng $\frac{4}{5}$.
Ta có sơ đồ:
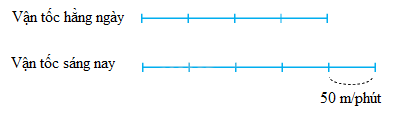
Vận tốc hằng ngày Anh đi đến trường là
50 : (5 – 4) x 4 = 200 (m/phút)
Quãng đường từ nhà Anh đến trường là
200 x 20 = 4000 (m) = 4 km
Đáp số: 4 km
BÀI TẬP ÁP DỤNG
Một người đi xe máy từ quê với vận tốc 40km/giờ, dự kiến tới Hà Nội lúc 8 giờ. Đi được nửa đường, người ấy phải dừng lại sửa xe mất nửa giờ. Sau đó người ấy phải đi với vận tốc 50 km/giờ để đến Hà Nội cho kịp giờ đã định. Tính quãng đường từ quê đến Hà Nội.
Một người đi xe máy từ A đến B gồm một đoạn lên dốc và một đoạn xuống dốc. Khi đi từ A đến B mất 3,5 giờ, khi trở về mất 4 giờ. Vận tốc khi lên dốc là 25km/giờ, vận tốc khi xuống dốc gấp đôi. Tính quãng đường AB?
Hằng ngày Anh đi xe đạp từ nhà đến trường mất 20 phút. Sáng nay, do có việc bận, Anh xuất phát chậm mất 4 phút so với mỗi ngày. Để đến trường đúng giờ, Anh tính mỗi phút phải đi nhanh hơn 50m so với mọi ngày. Hỏi quãng đường từ nhà Anh đến trường dài bao nhiêu ki-lô-mét?
Một ô tô đi từ A đến B. Người lái xe thấy rằng nếu xe đi với vận tốc 45 km/h thì đến B muộn 10 phút. Còn nếu xe đi với vận tốc 55 km/h thì đến B sớm 6 phút. Tính quãng đường AB.
Một ô tô dự định chạy từ tỉnh A sang tỉnh B lúc 16h nhưng:
- Nếu chạy với vận tốc 60km/h thì ô tô đến B lúc 15h.
- Nếu chạy với vận tốc 40 km/h thì ô tô đến B lúc 17h.
Hỏi ô tô phải chạy với vận tốc bao nhiêu để đến B đúng 16h.
Một ô tô đi quãng đường dài 225 km. Lúc đầu xe đi với vận tốc 60 km/h. Sau đó vì đường xấu và dốc nên vận tốc giảm xuống chỉ còn 35 km/h. Và vì vậy xe đi quãng đường đó hết 5 giờ. Tính thời gian xe đi với vận tốc 60km/h.
Dạng toán này tập trung vào các bài toán liên quan đến một vật thể chuyển động với vận tốc nhất định trong một khoảng thời gian nhất định, từ đó tính toán quãng đường đi được hoặc các yếu tố liên quan khác.
Để giải quyết dạng toán này, học sinh cần nắm vững các công thức cơ bản:
Ngoài ra, cần chú ý đến việc đổi đơn vị thời gian và vận tốc cho phù hợp với yêu cầu của bài toán (ví dụ: đổi phút sang giờ, km/giờ sang m/giây).
Để giải quyết các bài toán về chuyển động một cách hiệu quả, học sinh nên thực hiện theo các bước sau:
Bài tập: Một ô tô đi từ A đến B với vận tốc 60km/giờ trong 2 giờ. Tính quãng đường AB.
Giải:
Quãng đường AB là: 60km/giờ x 2 giờ = 120km
Đáp số: 120km
Dưới đây là một số bài tập luyện tập để học sinh củng cố kiến thức về dạng toán này:
Để học tốt dạng toán này, học sinh cần:
giaitoan.edu.vn hy vọng với những kiến thức và phương pháp giải trên, các em học sinh sẽ tự tin hơn khi đối mặt với các bài toán về chuyển động trong chương trình Toán nâng cao lớp 5.