Dạng toán này thường xuất hiện trong các bài thi toán nâng cao lớp 5, đòi hỏi học sinh phải nắm vững kiến thức về tỉ số và hiệu hai số. Bài học này sẽ giúp các em hiểu rõ phương pháp giải các bài toán liên quan đến tuổi, từ đó nâng cao kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp các em học sinh nắm vững kiến thức và tự tin giải các bài toán khó.
Mẹ sinh con năm mẹ 28 tuổi. Tổng số tuổi của hai mẹ con năm nay bằng 38 tuổi. Hỏi sau mấy năm nữa thì tuổi con bằng 5/12 tuổi mẹ?: Anh hơn em 8 tuổi. Khi tuổi anh bằng tuổi em hiện nay thì tuổi anh gấp 3 lần tuổi em. Tìm tuổi của mỗi người hiện nay.
Ví dụ 1: Năm nay anh 17 tuổi và em 8 tuổi. Hỏi cách đây mấy năm thì tuổi anh gấp 4 lần tuổi em?
Giải
Hiệu số tuổi của anh và em là:
17 – 8 = 9 (tuổi)
Vì hiệu số tuổi của hai anh em không thay đổi theo thời gian nên ta có sơ đồ biểu thị tuổi anh và tuổi em khi tuổi anh gấp 4 lần tuổi em:
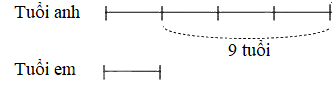
Tuổi em khi tuổi anh gấp 4 lần tuổi em là:
9 : (4 – 1) = 3 (tuổi)
Thời gian từ khi tuổi anh gấp 4 lần tuổi em cho đến nay là
8 – 3 = 5 (năm)
Đáp số: 5 năm
Ví dụ 2: Cách đây 2 năm con 5 tuổi và kém cha 30 tuổi. Hỏi sau bao nhiêu năm nữa thì tuổi cha gấp 3 lần tuổi con?
Giải
Tuổi con hiện nay là
5 + 2 = 7 (tuổi)
Vì hiệu số tuổi của hai cha con không thay đổi theo thời gian nên ta có sơ đồ biểu thị tuổi của hai cha con khi tuổi cha gấp 3 lần tuổi con:
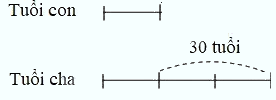
Tuổi con khi tuổi cha gấp 3 lần tuổi con là:
30 : (3 – 1) = 15 (tuổi)
Thời gian từ nay cho đến khi tuổi cha gấp 3 lần tuổi con là
15 – 7 = 8 (năm)
Đáp số: 8 năm
Ví dụ 3: Mẹ sinh con năm mẹ 28 tuổi. Tổng số tuổi của hai mẹ con năm nay bằng 38 tuổi. Hỏi sau mấy năm nữa thì tuổi con bằng $\frac{5}{{12}}$ tuổi mẹ?
Giải
Mẹ sinh con năm mẹ 28 tuổi nên hiêu số tuổi của hai mẹ con là 28 tuổi.
Tuổi con hiện nay là:
(38 – 28) : 2 = 5 (tuổi)
Ta có sơ đồ biểu thị tuổi của hai mẹ con khi tuổi con bằng $\frac{5}{{12}}$ tuổi mẹ:

Tuổi con khi đó là
28 : (12 – 5) x 5 = 20 (tuổi)
Thời gian từ nay cho đến khi tuổi con bằng $\frac{5}{{12}}$ tuổi mẹ là
20 – 5 = 15 (năm)
Đáp số: 15 năm
Ví dụ 4: Anh hơn em 8 tuổi. Khi tuổi anh bằng tuổi em hiện nay thì tuổi anh gấp 3 lần tuổi em. Tìm tuổi của mỗi người hiện nay.
Giải
Vì hiệu số tuổi của hai người không thay đổi theo thời gian nên ta có sơ đồ sau:
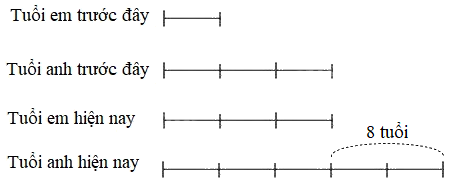
Tuổi em hiện nay là
8 : (5 – 3) x 3 = 12 (tuổi)
Tuổi anh hiện nay là 12 + 8 = 20 (tuổi)
Đáp số: Anh: 20 tuổi; em: 12 tuổi
Ví dụ 5: Năm nay tuổi cha gấp 4 lần tuổi con. Sau 20 năm nữa tuổi cha gấp đôi tuổi con. Tính tuổi của mỗi người hiện nay.
Giải
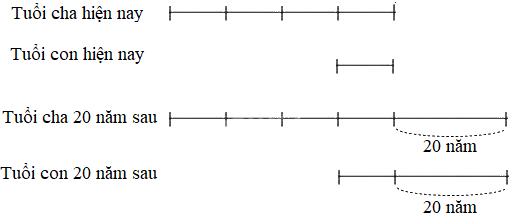
Theo sơ đồ, ta có 20 năm gấp 2 lần tuổi con hiện nay.
Tuổi con hiện nay là:
20 : 2 = 10 (tuổi)
Tuổi cha hiện nay là
10 x 4 = 40 (tuổi)
Đáp số: Con: 10 tuổi; cha: 40 tuổi
Dạng toán này là một phần quan trọng trong chương trình toán nâng cao lớp 5, thường xuyên xuất hiện trong các kỳ thi học sinh giỏi. Để giải quyết hiệu quả các bài toán thuộc dạng này, học sinh cần nắm vững các khái niệm cơ bản về tỉ số, hiệu hai số và mối quan hệ giữa chúng.
Trước khi đi vào giải các bài toán cụ thể, chúng ta cần ôn lại một số kiến thức quan trọng:
Có hai phương pháp chính để giải các bài toán về hiệu và tỉ số tuổi:
Ví dụ 1: Hai anh em có tổng số tuổi là 30. Biết tỉ số tuổi của anh và em là 2/1. Hỏi mỗi người bao nhiêu tuổi?
Giải:
Ta có sơ đồ:
Anh: |---|---|
Em: |---|
Tổng số phần bằng nhau là: 2 + 1 = 3 (phần)
Giá trị mỗi phần là: 30 / 3 = 10 (tuổi)
Tuổi của anh là: 10 * 2 = 20 (tuổi)
Tuổi của em là: 10 * 1 = 10 (tuổi)
Đáp số: Anh 20 tuổi, em 10 tuổi.
Ví dụ 2: Năm nay, mẹ hơn con 28 tuổi. Biết tỉ số tuổi của mẹ và con là 7/3. Hỏi mỗi người bao nhiêu tuổi?
Giải:
Ta có sơ đồ:
Mẹ: |---|---|---|---|---|---|---|
Con: |---|---|---|
Hiệu số phần là: 7 - 3 = 4 (phần)
Giá trị mỗi phần là: 28 / 4 = 7 (tuổi)
Tuổi của mẹ là: 7 * 7 = 49 (tuổi)
Tuổi của con là: 7 * 3 = 21 (tuổi)
Đáp số: Mẹ 49 tuổi, con 21 tuổi.
Để củng cố kiến thức, các em hãy tự giải các bài tập sau:
Để học tốt dạng toán này, các em cần:
Hy vọng với những kiến thức và phương pháp giải bài tập được trình bày trên đây, các em sẽ tự tin hơn khi đối mặt với các bài toán về hiệu và tỉ số tuổi trong chương trình toán nâng cao lớp 5.