Đây là một dạng toán quan trọng trong chương trình Toán nâng cao lớp 5, giúp học sinh rèn luyện kỹ năng giải toán phân số một cách linh hoạt và sáng tạo. Các bài toán thuộc dạng này thường yêu cầu học sinh vận dụng kiến thức về phân số, phép cộng, phép trừ và các quy tắc biến đổi phân số để tìm ra lời giải.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài tập có lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin làm bài tập.
Cho phân số 56/81. Hỏi cùng thêm vào tử số và mẫu số bao nhiêu đơn vị để được phân số bằng 3/4. Cho phân số 23/45 Hỏi phải cộng thêm vào tử số và bớt đi ở mẫu số cùng một số tự nhiên nào để được phân số mới có giá trị bằng 19/15
Phương pháp giải - Nếu ta cộng thêm(hoặc trừ đi) cả tử số và mẫu số của một phân số với cùng một số tự nhiên thì hiệu của tử số và mẫu số của phân số đó không thay đổi. - Nếu cộng thêm vào tử số đồng thời bớt đi ở mẫu số của một phân số với cùng một số tự nhiên thì tổng của tử số và mẫu số không thay đổi. - Nếu ta bớt đi ở tử số đồng thời thêm vào mẫu số của một phân số với cùng một số tự nhiên thì tổng của tử số và mẫu số không thay đổi. |
Ví dụ 1: Cho phân số . Hỏi cùng thêm vào tử số và mẫu số bao nhiêu đơn vị để được phân số bằng $\frac{3}{4}$ ?
Giải
Hiệu của mẫu số và tử số của phân số đã cho là 81 – 56 = 25
Khi ta thêm vào tử số và mẫu số cùng một số tự nhiên thì hiệu của mẫu số và tử số vẫn không đổi.
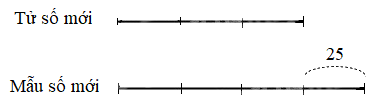
Tử số của phân số mới là 25 : (4 – 3) x 3 = 75
Số cần tìm là: 75 – 56 = 19
Đáp số: 19
Ví dụ 2: Cho phân số $\frac{{23}}{{45}}$. Hỏi phải cộng thêm vào tử số và bớt đi ở mẫu số cùng một số tự nhiên nào để được phân số mới có giá trị bằng$\frac{{19}}{{15}}$ ?
Giải
Tổng của tử số và mẫu số của phân số đã cho là 23 + 45 = 68
Khi ta cộng thêm vào tử số và bớt đi ở mẫu số cùng một số tự nhiên thì tổng của mẫu số và tử số vẫn không đổi và bằng 68.
Gọi số cần tìm là a. Ta có
$\frac{{23 + a}}{{45 - a}} = \frac{{19}}{{15}}$
Tổng số phần bằng nhau: 19 + 15 = 34 (phần)
Tử số của phân số mới là: 68 : 34 x 19 = 38
Ta có 23 + a = 38
Vậy a = 38 – 23 = 15
Đáp số: 15
Ví dụ 3: Cho phân số $\frac{{26}}{{45}}$. Hãy tìm số tự nhiên c sao cho đem mẫu số của phân số đã cho trừ đi c và giữ nguyên tử số ta được phân số mới có giá trị bằng $\frac{5}{6}$.
Giải:
Vì tử số giữ nguyên nên ta có:
$\frac{{25}}{{37 - c}} = \frac{5}{6} = \frac{{25}}{{30}}$
Hai phân số bằng nhau lại có tử số bằng nhau nên mẫu số của chúng cũng phải bằng nhau.
Tức là 37 – c = 30. Vậy c = 7.
Đáp số: c = 7
Ví dụ 4: Cho phân số $\frac{{26}}{{45}}$. Hãy tìm số tự nhiên c sao cho thêm c vào tử số và giữ nguyên mẫu số, ta được phân số mới có giá trị bằng $\frac{2}{3}$.
Giải:
Theo đề bài, ta có:
$\frac{{26 + c}}{{45}} = \frac{2}{3}$ hay $\frac{{26}}{{45}} + \frac{c}{{45}} = \frac{2}{3}$
Từ đó ta có: $\frac{c}{{45}} = \frac{2}{3} - \frac{{26}}{{45}} = \frac{4}{{45}}$
Vậy c = 4
Đáp số: c = 4
Bài tập áp dụng
Cho phân số $\frac{3}{7}$. Cộng thêm vào cả tử số và mẫu số cùa phân số đó với cùng một số tự nhiên ta được một phân số bằng $\frac{7}{9}$. Tìm số tự nhiên đó.
Khi bớt cả tử số và mẫu số của phân số $\frac{{71}}{{41}}$ đi cùng một số tự nhiên ta nhận được một phân số bằng $\frac{5}{2}$. Tìm số tự nhiên đó.
Cho phân số $\frac{7}{8}$. Hãy tìm số a sao cho đem tử số của phân số đã cho trừ đi a và thêm a vào mẫu số ta được một phân số mới bằng $\frac{1}{4}$.
Cho phân số $\frac{a}{b}$. Rút gọn phân số $\frac{a}{b}$ ta được phân số $\frac{2}{5}$. Nếu thêm vào tử số 45 đơn vị thì ta được phân số mới có giá trị bằng $\frac{{13}}{{20}}$. Tìm phân số $\frac{a}{b}$.
Cho phân số $\frac{{73}}{{97}}$. Hỏi cùng phải bớt ở tử số và mẫu số bao nhiêu đơn vị để được phân số mới có giá trị bằng $\frac{2}{3}$?
Dạng toán này thường xuất hiện trong các đề thi toán nâng cao lớp 5, đòi hỏi học sinh phải có tư duy logic và khả năng phân tích tốt. Để giải quyết các bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về phân số, bao gồm:
Có nhiều phương pháp khác nhau để giải các bài toán về thêm, bớt ở tử số và mẫu số. Dưới đây là một số phương pháp phổ biến:
Ví dụ 1: Một phân số có tổng của tử số và mẫu số là 120. Nếu thêm 15 vào tử số và bớt 15 ở mẫu số thì được phân số mới bằng 1. Tìm phân số ban đầu.
Giải:
Gọi phân số ban đầu là a/b. Ta có:
Từ phương trình thứ hai, ta có: a + 15 = b - 15 => a = b - 30
Thay a = b - 30 vào phương trình thứ nhất, ta có: b - 30 + b = 120 => 2b = 150 => b = 75
Suy ra: a = 75 - 30 = 45
Vậy phân số ban đầu là 45/75.
Ví dụ 2: Tìm một phân số, biết rằng nếu thêm 4 vào tử số và giữ nguyên mẫu số thì được phân số mới bằng 1. Nếu giữ nguyên tử số và bớt 4 ở mẫu số thì được phân số mới bằng 1/3.
Giải:
Gọi phân số cần tìm là a/b. Ta có:
Từ phương trình thứ nhất, ta có: a + 4 = b => a = b - 4
Thay a = b - 4 vào phương trình thứ hai, ta có: (b - 4) / (b - 4) = 1/3 (điều này không hợp lý, cần xem lại đề bài)
(Lưu ý: Ví dụ 2 có thể có lỗi trong đề bài, cần kiểm tra lại để đảm bảo tính chính xác.)
Dưới đây là một số bài tập luyện tập để giúp bạn củng cố kiến thức về dạng toán này:
Để học tốt dạng toán này, bạn cần:
Chúc bạn học tốt!