Đây là một dạng toán thường gặp trong chương trình toán nâng cao lớp 5, đòi hỏi học sinh phải nắm vững kiến thức về tỉ số và tổng. Bài học này sẽ giúp các em hiểu rõ cách giải các bài toán liên quan đến tuổi của hai người khi biết tổng số tuổi và tỉ số giữa chúng.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cách đây 8 năm tổng số tuổi của hai chị em bằng 24 tuổi. Hiện nay tuổi em bằng 3/5 tuổi chị... Hiện nay tổng số tuổi của hai của hai anh em bằng 22 tuổi. Khi tuổi anh bằng tuổi em hiện nay thì tuổi anh gấp 4 lần tuổi em.
Phương pháp giải - Các bài toán tính tuổi thuộc dạng toán có lời văn điển hình: tìm hai số khi biết tổng và tỉ số hoặc hiệu và tỉ số của hai số. - Đối với dạng toán này, người ta thường sử dụng phương pháp chia tỉ lệ để giải, trong đó, dùng sơ đồ đoạn thẳng để biểu thị mối quan hệ giữa các đại lượng tuổi trong từng thời kì (trước đây, hiện nay, sau này) - Hiệu số tuổi của hai người không thay đổi theo thời gian. - Trong các bài toán về tính tuổi, ta thường gặp các đại lượng sau: + Tuổi của A và B + Tổng số tuổi của A và B + Hiệu số tuổi của A và B + Tỉ số tuổi của A và B + Các thời điểm tính tuổi của A và B (trước đây, hiện nay và sau này) |
Ví dụ 1: Cách đây 8 năm tổng số tuổi của hai chị em bằng 24 tuổi. Hiện nay tuổi em bằng $\frac{3}{5}$ tuổi chị. Tìm tuổi của mỗi người hiện nay.
Giải
Sau mỗi năm, mỗi người tăng lên 1 tuổi nên tổng số tuổi của hai chị em hiện nay là:
24 + 8 x 2 = 40 (tuổi)
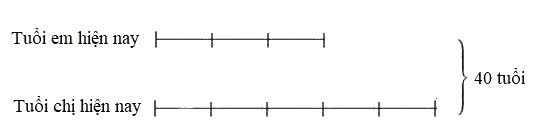
Tuổi em hiện nay là
40 : (3 + 5) x 3 = 15 (tuổi)
Tuổi chị hiện nay là
40 – 15 = 25 (tuổi)
Đáp số: Chị: 25 tuổi; Em: 15 tuổi
Ví dụ 2: Hai năm trước tổng số tuổi của hai cô cháu bằng 50 tuổi. Hiện nay 2 lần tuổi cô bằng 7 lần tuổi cháu. Tìm tuổi của mỗi người hiện nay.
Giải
Sau mỗi năm, mỗi người tăng lên 1 tuổi nên tổng số tuổi của hai cô cháu hiện nay là:
50 + 2 x 2 = 54 (tuổi)
Ta có sơ đồ biểu thị tuổi cô và tuổi cháu hiện nay:

Tuổi cháu hiện nay là:
54 : (7 + 2) x 2 = 12 (tuổi)
Tuổi cô hiện nay là:
54 – 12 = 42 (tuổi)
Đáp số: Cô: 42 tuổi; cháu: 12 tuổi
Ví dụ 3: Hiện nay tổng số tuổi của hai của hai anh em bằng 22 tuổi. Khi tuổi anh bằng tuổi em hiện nay thì tuổi anh gấp 4 lần tuổi em. Tính tuổi của mỗi người hiện nay.
Giải
Vì hiệu số tuổi của hai người không thay đổi theo thời gian nên ta có sơ đồ sau:
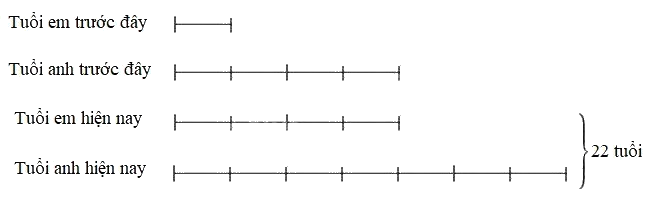
Tuổi em hiện nay:
22 : (4 + 7) x 4 = 8 (tuổi)
Tuổi anh hiện nay là:
22 – 8 = 14 (tuổi)
Đáp số: Anh: 14 tuổi ; em: 8 tuổi
Ví dụ 4: Hiện nay tổng số tuổi của hai chị em bằng 12 tuổi. Đến khi tuổi em bằng tuổi chị hiện nay thì tuổi chị bằng $\frac{5}{3}$ tuổi em. Tìm tuổi của mỗi người hiện nay.
Giải
Vì hiệu số tuổi của hai người không thay đổi theo thời gian nên ta có sơ đồ sau:
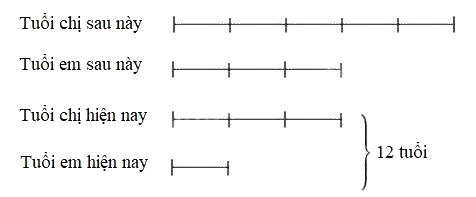
Tuổi em hiện nay là:
12 : (3 + 1) = 3 (tuổi)
Tuổi chị hiện nay là:
12 – 3 = 9 (tuổi)
Đáp số: Chị: 9 tuổi; 3 tuổi
Ví dụ 5: Hiện nay tuổi mẹ hơn 5 lần tuổi con là 3 tuổi. Đến khi tuổi con bằng tuổi mẹ hiện nay thì tổng số tuổi của hai mẹ con bằng 79 tuổi. Tìm tuổi của mỗi người hiện nay.
Giải
Vì hiệu số tuổi của hai người không thay đổi theo thời gian nên ta có sơ đồ sau:
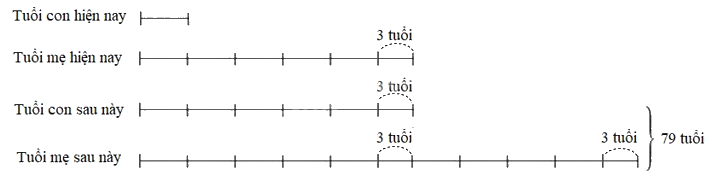
Tuổi con hiện nay là
(79 – 3 x 3) : (5 + 9) = 5 (tuổi)
Tuổi mẹ hiện nay là
5 x 5 + 3 = 28 (tuổi)
Đáp số: Con: 5 tuổi; mẹ: 28 tuổi
Dạng toán này là một phần quan trọng trong chương trình toán nâng cao lớp 5, giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề. Bài viết này sẽ cung cấp một hướng dẫn chi tiết về cách tiếp cận và giải quyết các bài toán thuộc dạng này.
Bài toán về tổng và tỉ số tuổi thường có cấu trúc như sau: Biết tổng số tuổi của hai người và tỉ số giữa tuổi của người này so với người kia. Mục tiêu là tìm tuổi của mỗi người.
Để giải quyết dạng toán này, chúng ta sử dụng phương pháp sau:
Ví dụ 1: Tổng số tuổi của hai anh em là 30 tuổi. Anh hơn em 6 tuổi. Tính tuổi của mỗi người.
Giải:
Ví dụ 2: Hiện nay, tuổi mẹ gấp 3 lần tuổi con. Sau 5 năm nữa, tổng số tuổi của hai mẹ con là 40 tuổi. Tính tuổi hiện tại của mỗi người.
Giải:
Dưới đây là một số bài tập để các em luyện tập:
Để giải nhanh các bài toán về tổng và tỉ số tuổi, các em có thể sử dụng sơ đồ đoạn thẳng để minh họa mối quan hệ giữa tuổi của hai người. Điều này sẽ giúp các em dễ dàng hình dung và tìm ra lời giải.
Dạng toán về tổng và tỉ số tuổi là một dạng toán quan trọng trong chương trình toán nâng cao lớp 5. Bằng cách nắm vững lý thuyết và luyện tập thường xuyên, các em sẽ có thể giải quyết các bài toán thuộc dạng này một cách dễ dàng và hiệu quả. giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức.