Chào mừng các em học sinh lớp 5 đến với bài học về Dạng 1: Tỉ số diện tích trong tam giác. Đây là một dạng toán nâng cao, đòi hỏi các em phải nắm vững kiến thức về diện tích tam giác và các tính chất liên quan.
Tại giaitoan.edu.vn, chúng tôi sẽ cung cấp cho các em những bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp các em hiểu sâu và giải quyết các bài toán một cách hiệu quả.
Cho tam giác ABC, lấy điểm N trên BC sao cho BN = 1/2 NC . Điểm M là trung điểm của AB. Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho AM gấp rưỡi MB; trên cạnh AC lấy điểm N sao cho AN bằng một nửa AC.
Phương pháp giải: - Hai tam giác chung đáy thì tỉ số diện tích bằng tỉ số 2 đường cao tương ứng. - Hai tam giác có chung đường cao thì tỉ số diện tích bằng tỉ số hai đáy tương ứng. |
Ví dụ 1. Cho tam giác ABC, lấy điểm N trên BC sao cho $BN = \frac{1}{2}NC$. Điểm M là trung điểm của AB. Tính diện tích tam giác ABC, biết diện tích tam giác BMN bằng 6 cm2.
Giải
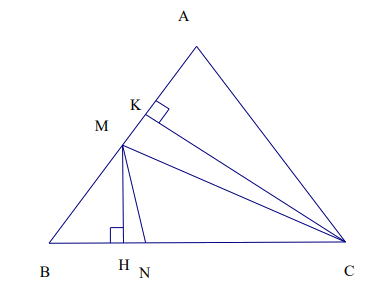
Kẻ đường cao MH, CK
Ta có ${S_{MBN}} = \frac{1}{2}{S_{MNC}}$(Hai tam giác có chung đường cao MH và $BN = \frac{1}{2}NC$)
Suy ra ${S_{MNC}} = 2 \times {S_{MBN}} = 2 \times 6 = 12$ (cm2)
${S_{BMC}} = {S_{MBN}} + {S_{MNC}} = 6 + 12 = 18$ (cm2)
Ta có ${S_{BMC}} = {S_{AMC}} = 18$ (cm2)
${S_{ABC}} = {S_{BMC}} + {S_{AMC}} = 18 + 18 = 36$ (cm2)
Đáp số: 36 cm2
Ví dụ 2. Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho AM gấp rưỡi MB; trên cạnh AC lấy điểm N sao cho AN bằng một nửa AC. Biết diện tích tam giác AMN là 36 cm2. Tính diện tích tứ giác BMNC.
Giải
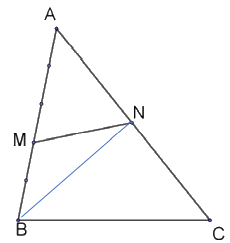
Ta có ${S_{MNB}} = \frac{2}{2}{S_{AMN}}$ (Chung chiều cao hạ từ đỉnh N xuống đáy AB và $MB = \frac{2}{3}MA$)
${S_{MNB}} = \frac{2}{3} \times 36 = 24$ (cm2)
${S_{ABN}} = {S_{AMN}} + {S_{MNB}} = 36 + 24 = 60$ (cm2)
${S_{ABN}} = {S_{BNC}} = 60\,(c{m^2})$ (Vì chung đường cao hạ từ đỉnh B và AN = NC)
Diện tích tứ giác BMNC là
${S_{BMNC}} = {S_{BMN}} + {S_{BNC}} = 24 + 60 = 84\,(c{m^2})$
Đáp số: 84 cm2
Cho tam giác ABC, trên AC lấy điểm N sao cho AN = $\frac{1}{4}$AC, trên BC lấy điểm M sao cho BM = MC. Kéo dài AB và MN cắt nhau ở P. Tính diện tích tam giác ABC biết diện tích tam giác APN bằng 100cm2.

(Đề thi vào lớp 6 môn Toán trường Hà Nội – Amsterdam 2003 – 2004)
Cho hình chữ nhật ABCD có diện tích 144cm2 như hình vẽ. Trên AB lấy điểm E, trên BC lấy điểm F. Các đoạn EB = $\frac{1}{3}$ x AB, CF = $\frac{1}{3}$ x CB. Tính diện tích tam giác DEF.

(Thi vào 6 trường THCS chuyên Ngoại Ngữ 2019 – 2020)
Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF?
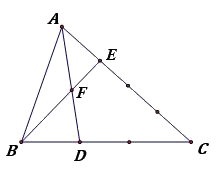
(Thi vào 6 trường Hà Nội Amsterdam 2006 – 2007)
Cho tam giác ABC có diện tích bằng 18cm2. Biết DA = 2 x DB; EC = 3 x EA; MC = MB (hình vẽ). Tính tổng diện tích hai tam giác MDB và MCE?
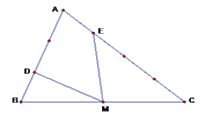
(Thi vào 6 trường Hà Nội Amsterdam 2001 – 2002)
Cho tam giác ABC và các điểm D, E, G, H sao cho BD = $\frac{1}{3}$ AB; AE = CG = $\frac{1}{3}$ AC; CH = $\frac{1}{3}$ BC. Tính diện tích hình BDEGH? Biết diện tích của tam giác ABC là 180cm2
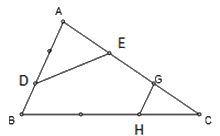
(Thi vào 6 trường Hà Nội Amsterdam 2010 – 2011)
Cho tam giác ABC có diện tích là 180 cm2. Biết AB = 3 x BM; AN = NP = PC; QB = QC. Tính diện tích tứ giác MNPQ? (xem hình vẽ)
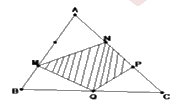
(Thi vào 6 trường Hà Nội Amsterdam 2013 – 2014)
Cho hình chữ nhật ABCD, F là một điểm bất kì trên cạnh AD, BF cắt CD kéo dài tại điểm E. Nối điểm A với điểm E. Tính diện tích tam giác AEF, biết AF = 3cm, BC = 5cm, AB = 7 cm?
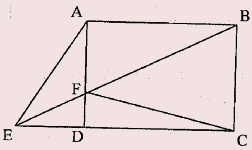
(Thi vào 6 trường Hà Nội Amsterdam 2011 – 2012)
Cho tam giác ABC biết BM = MC; CN = 3 x NA (như hình vẽ) và diện tích tam giác AEN bằng 27 cm². Tính diện tích tam giác ABC?
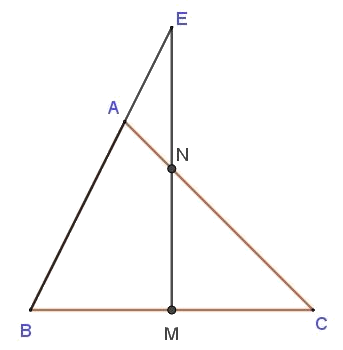
(Thi vào 6 trường Cầu Giấy năm 2020 – 2021)
Biết SKQBC = 26 cm2. Tỷ số $\frac{{BQ}}{{AB}} = \frac{1}{6}$; $\frac{{AK}}{{AC}} = \frac{1}{3}$.
Tính SAKQ.
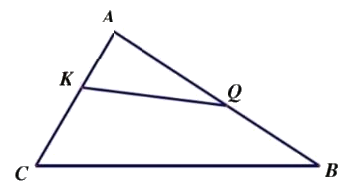
(Thi vào 6 trường Cầu Giấy năm 2019 – 2020)
Cho hình tam giác ABC. Lấy M trên AB và N trên AC sao cho AM = BM và NC x 2 = NA.
a) Tính tỉ số diện tích ANM và BMNC
b) Cho MN cắt BC ở D. So sánh BC với CD.
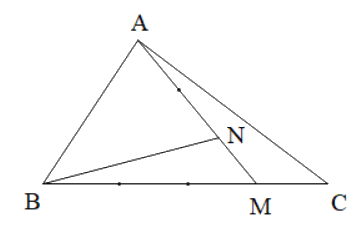
Cho tam giác ABC, M trên cạnh BC sao cho MB = $\frac{3}{4}$ BC; N trên cạnh AM sao cho AN = 2 NM. Biết diện tích tam giác NAB bằng 14dm2. Tính diện tích tam giác NMC.
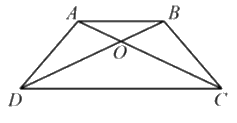
Cho hình thang ABCD có hai đáy AB, CD. Hai đường chéo AC và BD cắt nhau tại O. Biết diện tích tam giác OAD là 11 cm2, diện tích tam giác OAB là 5 cm2. Tính diện tích hình thang ABCD.
Chào mừng các em học sinh lớp 5 đến với chuyên đề toán nâng cao về tỉ số diện tích trong tam giác. Đây là một chủ đề quan trọng, giúp các em phát triển tư duy logic và khả năng giải quyết vấn đề trong môn Toán.
Trước khi đi vào giải các bài toán về tỉ số diện tích, chúng ta cần nắm vững một số kiến thức cơ bản sau:
Dạng 1: Tỉ số diện tích khi hai tam giác có chung đáy.
Ví dụ 1: Cho tam giác ABC có đáy BC = 10cm. Điểm D nằm trên BC sao cho BD = 3cm. Tính tỉ số diện tích của tam giác ABD và tam giác ADC.
Giải:
Tam giác ABD và tam giác ADC có chung đỉnh A và đáy BD và DC lần lượt nằm trên đáy BC.
Ta có: DC = BC - BD = 10cm - 3cm = 7cm.
Tỉ số diện tích của tam giác ABD và tam giác ADC là: SABD / SADC = BD / DC = 3/7.
Dạng 2: Tỉ số diện tích khi hai tam giác có chung chiều cao.
Ví dụ 2: Cho tam giác ABC có chiều cao AH = 8cm. Điểm D nằm trên BC sao cho BD = 5cm, DC = 3cm. Tính tỉ số diện tích của tam giác ABD và tam giác ADC.
Giải:
Tam giác ABD và tam giác ADC có chung đỉnh A và chiều cao AH.
Tỉ số diện tích của tam giác ABD và tam giác ADC là: SABD / SADC = BD / DC = 5/3.
Dạng 3: Tỉ số diện tích khi sử dụng tính chất đường trung bình của tam giác.
Ví dụ 3: Cho tam giác ABC, M là trung điểm của BC. Tính tỉ số diện tích của tam giác ABM và tam giác ABC.
Giải:
Vì M là trung điểm của BC nên BM = MC.
Tam giác ABM và tam giác ACM có chung đỉnh A và đáy BM = MC.
Do đó, SABM = SACM.
Tỉ số diện tích của tam giác ABM và tam giác ABC là: SABM / SABC = 1/2.
Hy vọng với những kiến thức và ví dụ trên, các em sẽ tự tin hơn khi giải các bài toán về tỉ số diện tích trong tam giác. Chúc các em học tốt!