Dạng toán này là một phần quan trọng trong chương trình Toán nâng cao lớp 5, giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề. Bài học này tập trung vào việc giải các bài toán liên quan đến hai vật thể chuyển động ngược chiều nhau, từ đó giúp các em hiểu rõ hơn về mối quan hệ giữa vận tốc, thời gian và quãng đường.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với hệ thống bài tập đa dạng, phong phú để hỗ trợ học sinh nắm vững kiến thức và tự tin giải các bài toán khó.
Lúc 5 giờ sáng bạn Nam đi xe đạp từ A về B với vận tốc 12 km/giờ. Đến 8 giờ, bạn Việt đi xe đạp từ B về A với vận tốc 15 km/giờ. Lúc 12 giờ trưa một ô tô khởi hành từ A đi về B. Cùng lúc đó một xe máy khởi hành từ B đi về A và hai xe gặp nhau tại địa điểm C cách A 180 km.
Phương pháp giải: Hai vật chuyển động ngược chiều với vận tốc v1 và v2, cùng thời điểm xuất phát và cách nhau quãng đường bằng s thì thời gian để chúng đi đến chỗ gặp nhau là: t = s : (v1 + v2) |
Ví dụ 1: Lúc 5 giờ sáng bạn Nam đi xe đạp từ A về B với vận tốc 12 km/giờ. Đến 8 giờ, bạn Việt đi xe đạp từ B về A với vận tốc 15 km/giờ. Hỏi 2 người gặp nhau lúc mấy giờ? Biết quãng đường AB dài 117 km. Địa điểm gặp nhau cách A bao nhiêu ki-lô-mét?
Giải
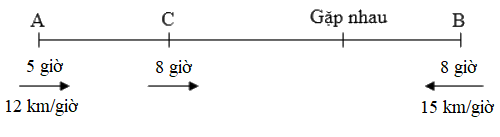
Thời gian bạn Nam đi trước là
8 – 5 = 3 (giờ)
Sau 3 giờ bạn Nam đi được quãng đường là
12 x 3 = 36 (km)
Khi đó, hai người còn cách nhau:
117 – 36 = 81 (km)
Thời gian từ lúc bạn Việt đi đến lúc gặp nhau là
81 : (12 + 15) = 3 (giờ)
Thời điểm hai người gặp nhau là
8 + 3 = 11 (giờ)
Địa điểm gặp nhau cách A số ki-lô-mét là
36 + 12 x 3 = 72 (km)
Đáp số: 11 giờ
72 km
Ví dụ 2: Lúc 12 giờ trưa một ô tô khởi hành từ A đi về B. Cùng lúc đó một xe máy khởi hành từ B đi về A và hai xe gặp nhau tại địa điểm C cách A 180 km. Tính vận tốc của mỗi xe, biết rằng vận tốc của ô tô lớn hơn vận tốc của xe máy là 15km/giờ và quãng đường AB dài 300km.
Giải
Quãng đường xe máy đi đến chỗ gặp nhau là:
300 – 180 = 120 (km)
Đến khi gặp nhau, tỉ số giữa quãng đường ô tô đi được và xe máy đi được là:
$180:120 = \frac{3}{2}$
Trong cùng một thời gian, quãng đường và vận tốc là hai đại lượng tỉ lệ thuận.
Suy ra tỉ số giữa vận tốc của ô tô và vận tốc của xe máy là $\frac{3}{2}$.
Ta có sơ đồ sau:
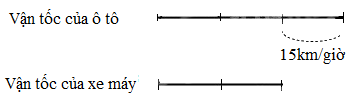
Vận tốc của ô tô là:
15 : (3 – 2) x 3 = 45 (km/giờ)
Vận tốc của xe máy là
45 – 15 = 30 (km//giờ)
Đáp số: Ô tô 45km/giờ ; xe máy: 30km/giờ
Ví dụ 3: Xe thứ nhất đi từ A đến B hết 3 giờ, xe thứ hai đi từ A đến B hết 2 giờ. Nếu lúc 10 giờ hai xe cùng khởi hành, xe thứ nhất xuất phát từ A đi đến B và xe thứ hai đi từ B về A thì lúc mấy giờ hai xe sẽ gặp nhau?
Giải
Xe thứ nhất đi từ A đến B hết 3 giờ nên 1 giờ xe thứ nhất đi được $\frac{1}{3}$ quãng đường AB.
Xe thứ hai đi từ A đến B hết 2 giờ nên 1 giờ xe thứ hai đi được $\frac{1}{2}$ quãng đường AB.
Trong 1 giờ cả 2 xe đi được:
$\frac{1}{3} + \frac{1}{2} = \frac{5}{6}$ (quãng đường AB)
Thời gian để hai xe đi đến chỗ gặp nhau là:
$1:\frac{5}{6} = 1,2$ (giờ)
1,2 giờ = 1 giờ 12 phút
Thời điểm hai xe gặp nhau là:
10 giờ + 1 giờ 12 phút = 11 giờ 12 phút
Đáp số: 11 giờ 12 phút
BÀI TẬP ÁP DỤNG
Hai thành phố A và B cách nhau 135 km. Một xe máy đi từ A đến B với vận tốc 42km/h và một xe đạp đi từ B đến A với vận tốc 12km/h. Hỏi sau bao lâu xe đạp và xe máy gặp nhau. Lúc gặp nhau xe máy cách B bao nhiêu km?
Hai thành phố A và B cách nhau 186 km. Lúc 6 giờ một người đi xe máy từ A với vận tốc 30km/giờ về B. Lúc 7 giờ một người khác đi xe máy từ B với vận tốc 35km/giờ về A. Hỏi lúc mấy giờ thì hai người gặp nhau và chỗ gặp nhau cách A bao xa?
Hai ô tô xuất phát từ A và B cùng một lúc và đi ngược chiều nhau. Quãng đường AB dài 162 km. Sau 2 giờ chúng gặp nhau. Tìm vận tốc của mỗi ô tô, biết vận tốc ô tô đi từ A bằng $\frac{4}{5}$ vận tốc ô tô đi từ B. Điểm gặp nhau cách A bao nhiêu km?
Một ô tô khởi hành tại A lúc 4 giờ sáng đi về B với vận tốc 60 km/h. Đến 5 giờ ô tô khác khởi hành tại B và đi về A với vận tốc 70 km/h. Hai xe gặp nhau lúc 8h. Tính khoảng cách từ A đến B.
Lúc 7 giờ sáng, một xe ô tô khởi hành từ A để đi về B với vận tốc 65km/giờ. Đến 8 giờ 30 phút một ô tô khác xuất phát từ B đi về A với vận tốc 75 km/giờ. Hỏi hai xe gặp nhau vào lúc mấy giờ? Biết rằng A cách B là 657,5 km.
Dạng toán về hai chuyển động ngược chiều là một trong những dạng toán thường gặp trong chương trình Toán nâng cao lớp 5. Đây là dạng toán đòi hỏi học sinh phải nắm vững kiến thức về vận tốc, thời gian, quãng đường và mối quan hệ giữa chúng. Bài viết này sẽ cung cấp một cách tiếp cận chi tiết và dễ hiểu để giải quyết các bài toán thuộc dạng này.
Trong các bài toán về hai chuyển động ngược chiều, hai vật thể xuất phát từ hai điểm khác nhau và di chuyển về phía nhau. Để giải quyết các bài toán này, chúng ta cần hiểu rõ các khái niệm sau:
Khi hai vật thể chuyển động ngược chiều, vận tốc tương đối của chúng là tổng vận tốc của mỗi vật thể. Điều này có nghĩa là chúng tiến lại gần nhau với tốc độ nhanh hơn.
Để giải các bài toán về hai chuyển động ngược chiều, chúng ta có thể áp dụng các bước sau:
Bài toán: Hai ô tô xuất phát từ hai địa điểm A và B cách nhau 240km. Ô tô thứ nhất khởi hành từ A với vận tốc 60km/giờ, ô tô thứ hai khởi hành từ B với vận tốc 40km/giờ. Hỏi sau bao lâu hai ô tô gặp nhau?
Giải:
Đáp số: Sau 2.4 giờ hai ô tô gặp nhau.
Dạng toán về hai chuyển động ngược chiều có thể xuất hiện trong nhiều hình thức khác nhau. Một số dạng bài tập thường gặp bao gồm:
Để củng cố kiến thức và kỹ năng giải bài toán về hai chuyển động ngược chiều, bạn có thể thực hành với các bài tập sau:
Dạng toán về hai chuyển động ngược chiều là một phần quan trọng trong chương trình Toán nâng cao lớp 5. Bằng cách nắm vững lý thuyết, phương pháp giải và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài toán thuộc dạng này. giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.