Chào mừng các em học sinh lớp 6 đến với bài trắc nghiệm về Bài 36: Góc trong chương trình Toán 6 Kết nối tri thức. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức đã học về góc, các loại góc và cách đo góc.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, từ dễ đến khó, kèm theo đáp án chi tiết để các em tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Cho hình vẽ sau
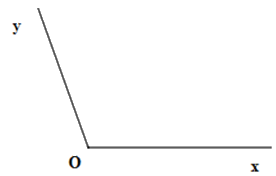
Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ
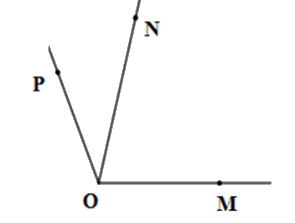
\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau
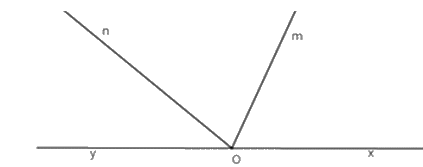
\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Lời giải và đáp án
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Đáp án : B
Sử dụng kiến thức về góc và so sánh hai góc
Để so sánh hai góc ta so sánh số đo của chúng
Ta có:
+ Góc là hình gồm hai tia chung gốc nên A đúng
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau
+ Hai góc bằng nhau có số đo bằng nhau nên C đúng
+ Hai góc có số đo bằng nhau thì bằng nhau nên D đúng
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Đáp án : C
Ta sử dụng kiến thức:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Số góc tạo thành là \(\dfrac{{9.\left( {9 - 1} \right)}}{2} = 36\) góc.
Cho hình vẽ sau
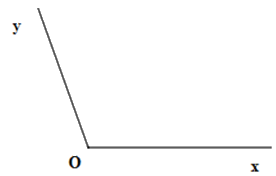
Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Đáp án : A
Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc.
Góc trên hình là góc \(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ
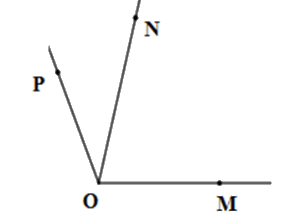
\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Đáp án : B
Quan sát hình vẽ, xác định các tia phân biệt chung gốc \(O\) từ đó tìm các góc tạo thành.
Các góc tạo thành là: \(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau
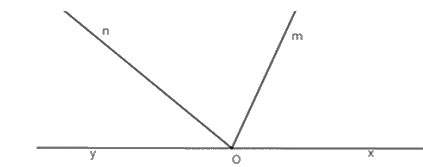
\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Đáp án : D
Xác định các tia chung gốc \(O\) từ đó xác định các góc có một cạnh là \(Om.\)
Các góc cần tìm là \(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\) .
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Đáp án : B
Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt.
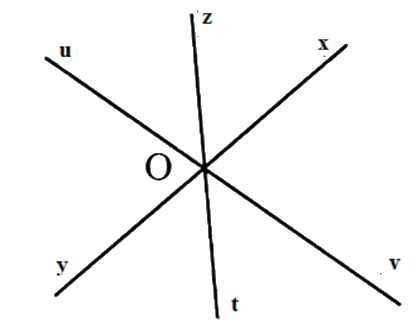
Các tia \(Ox\) và \(Oy;\) \(Oz\) và \(Ot;Ou\) và \(Ov\) là hai tia đối nhau nên các góc bẹt có đỉnh \(O\) tạo thành là
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\) .
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Đáp án : A
Sử dụng:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Từ đó tìm ra \(n.\)
Từ đề bài ta có \(\dfrac{{n\left( {n - 1} \right)}}{2} = 28\) nên \(n\left( {n - 1} \right) = 56\) mà \(56 = 8.7\), lại có $(n-1)$ và $n$ là hai số tự nhiên liên tiếp nên \(n = 8.\)
Vậy \(n = 8.\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Đáp án : C
Ta sử dụng công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Tính số góc ban đầu
+ Tính số góc sau khi thêm
+ Tính số góc tăng thêm
Số góc tạo thành khi có \(4\) tia chung gốc là \(\dfrac{{4.\left( {4 - 1} \right)}}{2} = 6\) góc
Số góc tạo thành khi có thêm ba tia chung gốc \(O\) nữa là \(\dfrac{{7.\left( {7 - 1} \right)}}{2} = 21\) góc
Số góc tăng thêm là \(21 - 6 = 15\) góc
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Đáp án : D
+ Xác định số lượng các tia phân biệt chung gốc \(O.\)
+ Tính góc theo công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Vì có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) nên số các tia chung gốc tạo thành là \(2n\) tia.
Số góc tạo thành là \(\dfrac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right)\) góc.
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Đáp án : C
Sử dụng: Khi hai tia \(Ox;Oy\) không đối nhau, điểm \(M\) là điểm nằm bên trong góc \(xOy\) nếu tia \(OM\) nằm giữa hai tia \(Ox;Oy\).
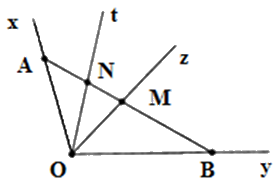
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) mà điểm \(N\) thuộc tia \(Ot\) nên điểm \(N\) nằm trong góc \(xOz\). Do đó A đúng.
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(N\) và điểm \(A\) nằm cùng phía đối với điểm \(M.\)
Tia \(Oz\) nằm giữa hai tia \(Ox;Oy\) nên điểm \(A;B\) nằm khác phía đối với điểm \(M.\) Suy ra điểm \(N\) và điểm \(B\) nằm khác phía đối với điểm \(M\), do đó điểm \(M\) nằm trong góc \(yOt.\) Do đó B đúng, D đúng.
Vì \(A \in Ox\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(A\) không nằm trong góc \(tOz.\) Do đó C sai.
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Cho hình vẽ sau

Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ

\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau

\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Đáp án : B
Sử dụng kiến thức về góc và so sánh hai góc
Để so sánh hai góc ta so sánh số đo của chúng
Ta có:
+ Góc là hình gồm hai tia chung gốc nên A đúng
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau
+ Hai góc bằng nhau có số đo bằng nhau nên C đúng
+ Hai góc có số đo bằng nhau thì bằng nhau nên D đúng
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Đáp án : C
Ta sử dụng kiến thức:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Số góc tạo thành là \(\dfrac{{9.\left( {9 - 1} \right)}}{2} = 36\) góc.
Cho hình vẽ sau

Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Đáp án : A
Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc.
Góc trên hình là góc \(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ

\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Đáp án : B
Quan sát hình vẽ, xác định các tia phân biệt chung gốc \(O\) từ đó tìm các góc tạo thành.
Các góc tạo thành là: \(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau

\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Đáp án : D
Xác định các tia chung gốc \(O\) từ đó xác định các góc có một cạnh là \(Om.\)
Các góc cần tìm là \(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\) .
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Đáp án : B
Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt.

Các tia \(Ox\) và \(Oy;\) \(Oz\) và \(Ot;Ou\) và \(Ov\) là hai tia đối nhau nên các góc bẹt có đỉnh \(O\) tạo thành là
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\) .
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Đáp án : A
Sử dụng:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Từ đó tìm ra \(n.\)
Từ đề bài ta có \(\dfrac{{n\left( {n - 1} \right)}}{2} = 28\) nên \(n\left( {n - 1} \right) = 56\) mà \(56 = 8.7\), lại có $(n-1)$ và $n$ là hai số tự nhiên liên tiếp nên \(n = 8.\)
Vậy \(n = 8.\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Đáp án : C
Ta sử dụng công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Tính số góc ban đầu
+ Tính số góc sau khi thêm
+ Tính số góc tăng thêm
Số góc tạo thành khi có \(4\) tia chung gốc là \(\dfrac{{4.\left( {4 - 1} \right)}}{2} = 6\) góc
Số góc tạo thành khi có thêm ba tia chung gốc \(O\) nữa là \(\dfrac{{7.\left( {7 - 1} \right)}}{2} = 21\) góc
Số góc tăng thêm là \(21 - 6 = 15\) góc
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Đáp án : D
+ Xác định số lượng các tia phân biệt chung gốc \(O.\)
+ Tính góc theo công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Vì có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) nên số các tia chung gốc tạo thành là \(2n\) tia.
Số góc tạo thành là \(\dfrac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right)\) góc.
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Đáp án : C
Sử dụng: Khi hai tia \(Ox;Oy\) không đối nhau, điểm \(M\) là điểm nằm bên trong góc \(xOy\) nếu tia \(OM\) nằm giữa hai tia \(Ox;Oy\).

Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) mà điểm \(N\) thuộc tia \(Ot\) nên điểm \(N\) nằm trong góc \(xOz\). Do đó A đúng.
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(N\) và điểm \(A\) nằm cùng phía đối với điểm \(M.\)
Tia \(Oz\) nằm giữa hai tia \(Ox;Oy\) nên điểm \(A;B\) nằm khác phía đối với điểm \(M.\) Suy ra điểm \(N\) và điểm \(B\) nằm khác phía đối với điểm \(M\), do đó điểm \(M\) nằm trong góc \(yOt.\) Do đó B đúng, D đúng.
Vì \(A \in Ox\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(A\) không nằm trong góc \(tOz.\) Do đó C sai.
Bài 36 trong chương trình Toán 6 Kết nối tri thức tập trung vào khái niệm góc, các loại góc (góc nhọn, góc vuông, góc tù, góc bẹt) và cách đo góc bằng thước đo góc. Việc nắm vững kiến thức này là nền tảng quan trọng cho các bài học hình học tiếp theo.
Các bài tập trắc nghiệm về Bài 36 thường xoay quanh các nội dung sau:
Câu 1: Góc có số đo bằng 90 độ là:
Đáp án: B. Góc vuông
Câu 2: Sử dụng thước đo góc, em đo được một góc có số đo là 60 độ. Vậy góc này là:
Đáp án: C. Góc nhọn
Để nắm vững kiến thức về Bài 36, các em nên:
Việc học tốt Bài 36 là bước đệm quan trọng để các em tiếp thu các kiến thức hình học phức tạp hơn trong các lớp học tiếp theo. Nắm vững kiến thức về góc sẽ giúp các em giải quyết các bài toán liên quan đến hình học một cách dễ dàng và hiệu quả hơn.
Hy vọng với bộ trắc nghiệm và các kiến thức được cung cấp trên giaitoan.edu.vn, các em sẽ học tốt Bài 36: Góc Toán 6 Kết nối tri thức và đạt kết quả cao trong các kỳ thi.