Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, bám sát chương trình học Toán 6 Kết nối tri thức, tập trung vào các dạng toán về mở rộng khái niệm phân số và phân số bằng nhau. Bài tập được thiết kế giúp học sinh củng cố kiến thức, rèn luyện kỹ năng giải nhanh và chính xác.
Với giao diện thân thiện, dễ sử dụng, học sinh có thể tự học tại nhà hoặc sử dụng như một công cụ hỗ trợ cho việc học trên lớp. Hãy cùng giaitoan.edu.vn chinh phục môn Toán một cách hiệu quả!
Hãy viết phép chia sau đưới dạng phân số: $\left( { - 58} \right):73$
\(\dfrac{{ - 58}}{{73}}\)
\(\dfrac{{58}}{{73}}\)
\(\dfrac{{73}}{{ - 58}}\)
\(\dfrac{{58}}{{73}}\)
Phần tô màu trong hình sau biểu diễn phân số nào?

\(\dfrac{1}{2}\)
\(\dfrac{1}{4}\)
\(\dfrac{3}{4}\)
\(\dfrac{5}{8}\)
Chọn câu sai?
\(\dfrac{1}{3} = \dfrac{{45}}{{135}}\)
\(\dfrac{{ - 13}}{{20}} = \dfrac{{26}}{{ - 40}}\)
\(\dfrac{{ - 4}}{{15}} = \dfrac{{ - 16}}{{ - 60}}\)
\(\dfrac{6}{7} = \dfrac{{ - 42}}{{ - 49}}\)
Tìm số nguyên \(x\) biết \(\dfrac{{35}}{{15}} = \dfrac{x}{3}?\)
\(x = 7\)
\(x = 5\)
\(x = 15\)
\(x = 6\)
Viết \(20\,d{m^2}\) dưới dạng phân số với đơn vị là mét vuông.
\(\dfrac{{100}}{{20}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{100}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{10}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{1000}}\left( {{m^2}} \right)\)
Cho biểu thức \(C = \dfrac{{11}}{{2n + 1}}\) . Tìm tất cả các giá trị của $n$ nguyên để giá trị của $C$ là một số tự nhiên.
\(n \in \left\{ { - 6; - 1;0;5} \right\}\)
\(n \in \left\{ { - 1;5} \right\}\)
\(n \in \left\{ {0;5} \right\}\)
\(n \in \left\{ {1;11} \right\}\)
Có bao nhiêu giá trị nguyên dương của \(n\) để \(\dfrac{9}{{4n + 1}}\) đạt giá trị nguyên.
\(1\)
\(0\)
\(2\)
\(3\)
Cho các phân số: \(\dfrac{{15}}{{60}};\dfrac{{ - 7}}{5};\dfrac{6}{{15}};\dfrac{{28}}{{ - 20}};\dfrac{3}{{12}}\)
Số cặp phân số bằng nhau trong những phân số trên là:
\(4\)
\(1\)
\(3\)
\(2\)
Tính tổng các giá trị \(x \in Z\) biết rằng \( - \dfrac{{111}}{{37}} < x < \dfrac{{91}}{{13}}.\)
\(22\)
\(20\)
\(18\)
\(15\)
Tìm tập hợp các số nguyên \(n\) để \(A = \dfrac{{3n - 5}}{{n + 4}}\) có giá trị là số nguyên.
\(n \in \left\{ {13} \right\}\)
\(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
\(n \in \left\{ { - 17; - 1;1;17} \right\}\)
\(n \in \left\{ { - 13; - 3;3;13} \right\}\)
Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(\dfrac{x}{5} = \dfrac{3}{y}\) và \(x > y?\)
\(4\)
\(3\)
\(2\)
\(1\)
Tìm \(x;y\) biết \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) và \(x - y = 5.\)
\(x = 15;y = 5\)
\(x = 5;y = 15\)
\(x = 20;y = 15\)
\(x = 25;y = 10\)
Tìm số nguyên \(x\) biết rằng \(\dfrac{x}{3} = \dfrac{{27}}{x}\) và \(x < 0.\)
\(x = 81\)
\(x = - 81\)
\(x = - 9\)
\(x = 9\)
Viết số nguyên \(a\) dưới dạng phân số ta được:
\(\dfrac{a}{0}\)
\(\dfrac{0}{a}\)
\(\dfrac{a}{1}\)
\(\dfrac{1}{a}\)
Cách viết nào sau đây cho ta một phân số:
\(\dfrac{4}{0}\)
\(\dfrac{{1,5}}{3}\)
\(\dfrac{0}{7}\)
\(\dfrac{{ - 5}}{{3,5}}\)
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là:
Chín phần bảy
Âm bảy phần chín
Bảy phần chín
Âm chín phần bảy
Lời giải và đáp án
Hãy viết phép chia sau đưới dạng phân số: $\left( { - 58} \right):73$
\(\dfrac{{ - 58}}{{73}}\)
\(\dfrac{{58}}{{73}}\)
\(\dfrac{{73}}{{ - 58}}\)
\(\dfrac{{58}}{{73}}\)
Đáp án : A
Phân số \(\dfrac{a}{b}\) với \(a,b \in Z,b \ne 0\) được viết dưới dạng phép chia là \(a:b\)
Phép chia $\left( { - 58} \right):73$ được viết dưới dạng phân số là \(\dfrac{{ - 58}}{{73}}\)
Phần tô màu trong hình sau biểu diễn phân số nào?

\(\dfrac{1}{2}\)
\(\dfrac{1}{4}\)
\(\dfrac{3}{4}\)
\(\dfrac{5}{8}\)
Đáp án : B
Quan sát hình vẽ, đếm số ô vuông có trong hình và số ô vuông được tô màu, phân số biểu thị có tử là số ô vuông tô màu và mẫu là tổng số ô vuông có trong hình.
Trong hình có \(2\) ô vuông tô màu và tổng tất cả \(8\) ô vuông nên phân số biểu thị là \(\dfrac{2}{8} = \dfrac{1}{4}\)
Chọn câu sai?
\(\dfrac{1}{3} = \dfrac{{45}}{{135}}\)
\(\dfrac{{ - 13}}{{20}} = \dfrac{{26}}{{ - 40}}\)
\(\dfrac{{ - 4}}{{15}} = \dfrac{{ - 16}}{{ - 60}}\)
\(\dfrac{6}{7} = \dfrac{{ - 42}}{{ - 49}}\)
Đáp án : C
Kiểm tra tính đúng sai của từng đáp án bằng cách sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Đáp án A: Vì \(1.135 = 3.45\) nên \(\dfrac{1}{3} = \dfrac{{45}}{{135}}\)
\( \Rightarrow A\) đúng.
Đáp án B: Vì \(\left( { - 13} \right).\left( { - 40} \right) = 20.26\) nên \(\dfrac{{ - 13}}{{20}} = \dfrac{{26}}{{ - 40}}\)
\( \Rightarrow B\) đúng.
Đáp án C: Vì \(\left( { - 4} \right).\left( { - 60} \right) \ne 15.\left( { - 16} \right)\) nên \(\dfrac{{ - 4}}{{15}} \ne \dfrac{{ - 16}}{{ - 60}}\)
\( \Rightarrow C\) sai.
Đáp án D: Vì \(6.\left( { - 49} \right) = 7.\left( { - 42} \right)\) nên \(\dfrac{6}{7} = \dfrac{{ - 42}}{{ - 49}}\)
\( \Rightarrow D\) đúng.
Tìm số nguyên \(x\) biết \(\dfrac{{35}}{{15}} = \dfrac{x}{3}?\)
\(x = 7\)
\(x = 5\)
\(x = 15\)
\(x = 6\)
Đáp án : A
Sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
\(\begin{array}{l}\dfrac{{35}}{{15}} = \dfrac{x}{3}\\35.3 = 15.x\\x = \dfrac{{35.3}}{{15}}\\x = 7\end{array}\)
Vậy \(x = 7\)
Viết \(20\,d{m^2}\) dưới dạng phân số với đơn vị là mét vuông.
\(\dfrac{{100}}{{20}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{100}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{10}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{1000}}\left( {{m^2}} \right)\)
Đáp án : B
Đổi đơn vị với chú ý \(1{m^2} = 100d{m^2}\) hay \(1d{m^2} = \dfrac{1}{{100}}{m^2}\)
Ta có: \(20\,d{m^2} = \dfrac{{20}}{{100}}{m^2}\)
Cho biểu thức \(C = \dfrac{{11}}{{2n + 1}}\) . Tìm tất cả các giá trị của $n$ nguyên để giá trị của $C$ là một số tự nhiên.
\(n \in \left\{ { - 6; - 1;0;5} \right\}\)
\(n \in \left\{ { - 1;5} \right\}\)
\(n \in \left\{ {0;5} \right\}\)
\(n \in \left\{ {1;11} \right\}\)
Đáp án : C
- $C$ là số tự nhiên suy ra \(C\) là số nguyên hay $2n + 1$ là ước của $11$ - Từ đó tìm các giá trị của $n$ rồi thử lại kiểm tra lại điều kiện \(C\) là số tự nhiên.
Vì \(C \in N\) nên \(\frac{11}{2n+1} \in N.\)
Để \(\frac{11}{2n+1} \in N\) thì \(11 \vdots (2n+1)\) và \((2n+1) > 0\) hay \((2n+1) \in \left\{ { 1; 11} \right\}\)
Ta có bảng:
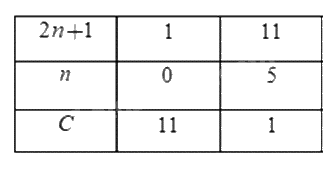
Vì \(C \in N\) nên ta nhận các giá trị \(n = 0;n = 5\)
Có bao nhiêu giá trị nguyên dương của \(n\) để \(\dfrac{9}{{4n + 1}}\) đạt giá trị nguyên.
\(1\)
\(0\)
\(2\)
\(3\)
Đáp án : A
Phân số \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\) là một số nguyên nếu \(b\) là ước của $a$
Vì \(n\) nguyên dương nên để \(\dfrac{9}{{4n + 1}}\) nguyên thì \(4n + 1 \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)
Ta có bảng:
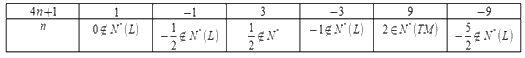
Vậy có duy nhất một giá trị của \(n\) thỏa mãn là \(n = 2\)
Cho các phân số: \(\dfrac{{15}}{{60}};\dfrac{{ - 7}}{5};\dfrac{6}{{15}};\dfrac{{28}}{{ - 20}};\dfrac{3}{{12}}\)
Số cặp phân số bằng nhau trong những phân số trên là:
\(4\)
\(1\)
\(3\)
\(2\)
Đáp án : D
- Ta sẽ chia các phân số thành \(2\) loại: phân số dương, phân số âm (chú ý phân số dương và phân số âm không thể bằng nhau)
- Tìm các cặp phân số bằng nhau trong những phân số dương và các cặp phân số bằng nhau trong những phân số âm rồi kết luận.
Sử dụng kiến thức:
- Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
- Định nghĩa các phân số dương, phân số âm:
+ Phân số âm: là phân số có tử và mẫu là các số nguyên trái dấu.
+ Phân số dương: là phân số có tử và mẫu là các số nguyên cùng dấu.
- Các phân số dương: \(\dfrac{{15}}{{60}};\dfrac{6}{{15}};\dfrac{3}{{12}}\)
+ Vì \(15.15 \ne 60.6\) nên \(\dfrac{{15}}{{60}} \ne \dfrac{6}{{15}}\)
+ Vì \(6.12 \ne 15.3\) nên \(\dfrac{6}{{15}} \ne \dfrac{3}{{12}}\)
+ Vì \(15.12 = 60.3\) nên \(\dfrac{{15}}{{60}} = \dfrac{3}{{12}}\)
- Các phân số âm: \(\dfrac{{ - 7}}{5};\dfrac{{28}}{{ - 20}}\)
Vì \(\left( { - 7} \right).\left( { - 20} \right) = 5.28\) nên \(\dfrac{{ - 7}}{5} = \dfrac{{28}}{{ - 20}}\)
Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.
Tính tổng các giá trị \(x \in Z\) biết rằng \( - \dfrac{{111}}{{37}} < x < \dfrac{{91}}{{13}}.\)
\(22\)
\(20\)
\(18\)
\(15\)
Đáp án : C
Tính giá trị các phân số rồi tìm các số nguyên \(x\) thỏa mãn.
Ta có: \(- \dfrac{{111}}{{37}} < x < \dfrac{{91}}{{13}}\)
Mà \( - \dfrac{{111}}{{37}} < -3; 7 < \dfrac{{91}}{{13}}\)
\(\begin{array}{l} \Rightarrow - 3 < x < 7\\ \Rightarrow x \in \left\{ { - 2; - 1;0;1;2;3;4;5;6} \right\}\end{array}\)
Vậy tổng các giá trị của \(x\) thỏa mãn là: \(\left( { - 2} \right) + \left( { - 1} \right) + ... + 5 + 6 = 18\)
Tìm tập hợp các số nguyên \(n\) để \(A = \dfrac{{3n - 5}}{{n + 4}}\) có giá trị là số nguyên.
\(n \in \left\{ {13} \right\}\)
\(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
\(n \in \left\{ { - 17; - 1;1;17} \right\}\)
\(n \in \left\{ { - 13; - 3;3;13} \right\}\)
Đáp án : B
- Biến đổi \(A\) về dạng \(A = a + \dfrac{b}{{n + 4}}\) với \(a,b \in Z\)
- Để \(A\) nguyên thì \(n + 4 \in U\left( b \right)\)
Ta có:
\(A = \dfrac{{3n - 5}}{{n + 4}} = \dfrac{{3n + 12 - 12 - 5}}{{n + 4}}\)\( = \dfrac{{3\left( {n + 4} \right) + \left( { - 17} \right)}}{{n + 4}}\) \( = \dfrac{{3\left( {n + 4} \right)}}{{n + 4}} + \dfrac{{ - 17}}{{n + 4}} = 3 + \dfrac{{ - 17}}{{n + 4}}\)
Vì \(n \in Z\) nên để \(A \in Z\) thì \(n + 4 \in U\left( { - 17} \right) = \left\{ { \pm 1; \pm 17} \right\}\)
Ta có bảng:

Vậy \(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(\dfrac{x}{5} = \dfrac{3}{y}\) và \(x > y?\)
\(4\)
\(3\)
\(2\)
\(1\)
Đáp án : A
Sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Ta có: \(\dfrac{x}{5} = \dfrac{3}{y}\)\( \Rightarrow x.y = 5.3 = 15\)
Mà \(15 = 5.3 = 15.1 = \left( { - 3} \right).\left( { - 5} \right) = \left( { - 1} \right).\left( { - 15} \right)\) và \(x,y \in Z,x > y\) nên \(\left( {x;y} \right) \in \left\{ {\left( {5;3} \right),\left( {15;1} \right),\left( { - 3; - 5} \right),\left( { - 1; - 15} \right)} \right\}\)
Tìm \(x;y\) biết \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) và \(x - y = 5.\)
\(x = 15;y = 5\)
\(x = 5;y = 15\)
\(x = 20;y = 15\)
\(x = 25;y = 10\)
Đáp án : C
- Rút \(x\) theo \(y\) từ điều kiện đơn giản rồi thay vào đẳng thức hai phân số bằng nhau.
- Sử dụng kiến thức hai phân số bằng nhau để tìm \(y,\) từ đó suy ra \(x\)
- Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Ta có: \(x - y = 5 \Rightarrow x = y + 5\) thay vào \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) ta được:
\(\begin{array}{l}\dfrac{{y + 5 - 4}}{{y - 3}} = \dfrac{4}{3}\\\dfrac{{y + 1}}{{y - 3}} = \dfrac{4}{3}\\3\left( {y + 1} \right) = 4\left( {y - 3} \right)\\3y + 3 = 4y - 12\\3y - 4y = - 12 - 3\\ - y = - 15\\y = 15\\ \Rightarrow x = 15 + 5 = 20\end{array}\)
Vậy \(x = 20;y = 15\)
Tìm số nguyên \(x\) biết rằng \(\dfrac{x}{3} = \dfrac{{27}}{x}\) và \(x < 0.\)
\(x = 81\)
\(x = - 81\)
\(x = - 9\)
\(x = 9\)
Đáp án : C
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau).
\(\begin{array}{l}\dfrac{x}{3} = \dfrac{{27}}{x}\\x.x = 81\\{x^2} = 81\end{array}\)
Ta có: \(x = 9\) hoặc \(x = - 9\)
Kết hợp điều kiện \(x < 0\) nên có một giá trị \(x\) thỏa mãn là: \(x = - 9\)
Viết số nguyên \(a\) dưới dạng phân số ta được:
\(\dfrac{a}{0}\)
\(\dfrac{0}{a}\)
\(\dfrac{a}{1}\)
\(\dfrac{1}{a}\)
Đáp án : C
Viết số nguyên \(a\) dưới dạng phân số ta được: \(\dfrac{a}{1}\).
Cách viết nào sau đây cho ta một phân số:
\(\dfrac{4}{0}\)
\(\dfrac{{1,5}}{3}\)
\(\dfrac{0}{7}\)
\(\dfrac{{ - 5}}{{3,5}}\)
Đáp án : C
+ \(\dfrac{4}{0}\) có mẫu bằng \(0\) nên không là phân số
+ \(\dfrac{{1,5}}{3}\) có \(1,5 \notin \mathbb{Z}\) nên không là phân số
+ \(\dfrac{0}{7}\) là phân số
+ \(\dfrac{{ - 5}}{{3,5}}\) có \(3,5 \notin \mathbb{Z}\) nên không là phân số
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là:
Chín phần bảy
Âm bảy phần chín
Bảy phần chín
Âm chín phần bảy
Đáp án : D
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là: Âm chín phần bảy
Hãy viết phép chia sau đưới dạng phân số: $\left( { - 58} \right):73$
\(\dfrac{{ - 58}}{{73}}\)
\(\dfrac{{58}}{{73}}\)
\(\dfrac{{73}}{{ - 58}}\)
\(\dfrac{{58}}{{73}}\)
Phần tô màu trong hình sau biểu diễn phân số nào?

\(\dfrac{1}{2}\)
\(\dfrac{1}{4}\)
\(\dfrac{3}{4}\)
\(\dfrac{5}{8}\)
Chọn câu sai?
\(\dfrac{1}{3} = \dfrac{{45}}{{135}}\)
\(\dfrac{{ - 13}}{{20}} = \dfrac{{26}}{{ - 40}}\)
\(\dfrac{{ - 4}}{{15}} = \dfrac{{ - 16}}{{ - 60}}\)
\(\dfrac{6}{7} = \dfrac{{ - 42}}{{ - 49}}\)
Tìm số nguyên \(x\) biết \(\dfrac{{35}}{{15}} = \dfrac{x}{3}?\)
\(x = 7\)
\(x = 5\)
\(x = 15\)
\(x = 6\)
Viết \(20\,d{m^2}\) dưới dạng phân số với đơn vị là mét vuông.
\(\dfrac{{100}}{{20}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{100}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{10}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{1000}}\left( {{m^2}} \right)\)
Cho biểu thức \(C = \dfrac{{11}}{{2n + 1}}\) . Tìm tất cả các giá trị của $n$ nguyên để giá trị của $C$ là một số tự nhiên.
\(n \in \left\{ { - 6; - 1;0;5} \right\}\)
\(n \in \left\{ { - 1;5} \right\}\)
\(n \in \left\{ {0;5} \right\}\)
\(n \in \left\{ {1;11} \right\}\)
Có bao nhiêu giá trị nguyên dương của \(n\) để \(\dfrac{9}{{4n + 1}}\) đạt giá trị nguyên.
\(1\)
\(0\)
\(2\)
\(3\)
Cho các phân số: \(\dfrac{{15}}{{60}};\dfrac{{ - 7}}{5};\dfrac{6}{{15}};\dfrac{{28}}{{ - 20}};\dfrac{3}{{12}}\)
Số cặp phân số bằng nhau trong những phân số trên là:
\(4\)
\(1\)
\(3\)
\(2\)
Tính tổng các giá trị \(x \in Z\) biết rằng \( - \dfrac{{111}}{{37}} < x < \dfrac{{91}}{{13}}.\)
\(22\)
\(20\)
\(18\)
\(15\)
Tìm tập hợp các số nguyên \(n\) để \(A = \dfrac{{3n - 5}}{{n + 4}}\) có giá trị là số nguyên.
\(n \in \left\{ {13} \right\}\)
\(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
\(n \in \left\{ { - 17; - 1;1;17} \right\}\)
\(n \in \left\{ { - 13; - 3;3;13} \right\}\)
Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(\dfrac{x}{5} = \dfrac{3}{y}\) và \(x > y?\)
\(4\)
\(3\)
\(2\)
\(1\)
Tìm \(x;y\) biết \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) và \(x - y = 5.\)
\(x = 15;y = 5\)
\(x = 5;y = 15\)
\(x = 20;y = 15\)
\(x = 25;y = 10\)
Tìm số nguyên \(x\) biết rằng \(\dfrac{x}{3} = \dfrac{{27}}{x}\) và \(x < 0.\)
\(x = 81\)
\(x = - 81\)
\(x = - 9\)
\(x = 9\)
Viết số nguyên \(a\) dưới dạng phân số ta được:
\(\dfrac{a}{0}\)
\(\dfrac{0}{a}\)
\(\dfrac{a}{1}\)
\(\dfrac{1}{a}\)
Cách viết nào sau đây cho ta một phân số:
\(\dfrac{4}{0}\)
\(\dfrac{{1,5}}{3}\)
\(\dfrac{0}{7}\)
\(\dfrac{{ - 5}}{{3,5}}\)
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là:
Chín phần bảy
Âm bảy phần chín
Bảy phần chín
Âm chín phần bảy
Hãy viết phép chia sau đưới dạng phân số: $\left( { - 58} \right):73$
\(\dfrac{{ - 58}}{{73}}\)
\(\dfrac{{58}}{{73}}\)
\(\dfrac{{73}}{{ - 58}}\)
\(\dfrac{{58}}{{73}}\)
Đáp án : A
Phân số \(\dfrac{a}{b}\) với \(a,b \in Z,b \ne 0\) được viết dưới dạng phép chia là \(a:b\)
Phép chia $\left( { - 58} \right):73$ được viết dưới dạng phân số là \(\dfrac{{ - 58}}{{73}}\)
Phần tô màu trong hình sau biểu diễn phân số nào?

\(\dfrac{1}{2}\)
\(\dfrac{1}{4}\)
\(\dfrac{3}{4}\)
\(\dfrac{5}{8}\)
Đáp án : B
Quan sát hình vẽ, đếm số ô vuông có trong hình và số ô vuông được tô màu, phân số biểu thị có tử là số ô vuông tô màu và mẫu là tổng số ô vuông có trong hình.
Trong hình có \(2\) ô vuông tô màu và tổng tất cả \(8\) ô vuông nên phân số biểu thị là \(\dfrac{2}{8} = \dfrac{1}{4}\)
Chọn câu sai?
\(\dfrac{1}{3} = \dfrac{{45}}{{135}}\)
\(\dfrac{{ - 13}}{{20}} = \dfrac{{26}}{{ - 40}}\)
\(\dfrac{{ - 4}}{{15}} = \dfrac{{ - 16}}{{ - 60}}\)
\(\dfrac{6}{7} = \dfrac{{ - 42}}{{ - 49}}\)
Đáp án : C
Kiểm tra tính đúng sai của từng đáp án bằng cách sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Đáp án A: Vì \(1.135 = 3.45\) nên \(\dfrac{1}{3} = \dfrac{{45}}{{135}}\)
\( \Rightarrow A\) đúng.
Đáp án B: Vì \(\left( { - 13} \right).\left( { - 40} \right) = 20.26\) nên \(\dfrac{{ - 13}}{{20}} = \dfrac{{26}}{{ - 40}}\)
\( \Rightarrow B\) đúng.
Đáp án C: Vì \(\left( { - 4} \right).\left( { - 60} \right) \ne 15.\left( { - 16} \right)\) nên \(\dfrac{{ - 4}}{{15}} \ne \dfrac{{ - 16}}{{ - 60}}\)
\( \Rightarrow C\) sai.
Đáp án D: Vì \(6.\left( { - 49} \right) = 7.\left( { - 42} \right)\) nên \(\dfrac{6}{7} = \dfrac{{ - 42}}{{ - 49}}\)
\( \Rightarrow D\) đúng.
Tìm số nguyên \(x\) biết \(\dfrac{{35}}{{15}} = \dfrac{x}{3}?\)
\(x = 7\)
\(x = 5\)
\(x = 15\)
\(x = 6\)
Đáp án : A
Sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
\(\begin{array}{l}\dfrac{{35}}{{15}} = \dfrac{x}{3}\\35.3 = 15.x\\x = \dfrac{{35.3}}{{15}}\\x = 7\end{array}\)
Vậy \(x = 7\)
Viết \(20\,d{m^2}\) dưới dạng phân số với đơn vị là mét vuông.
\(\dfrac{{100}}{{20}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{100}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{10}}\left( {{m^2}} \right)\)
\(\dfrac{{20}}{{1000}}\left( {{m^2}} \right)\)
Đáp án : B
Đổi đơn vị với chú ý \(1{m^2} = 100d{m^2}\) hay \(1d{m^2} = \dfrac{1}{{100}}{m^2}\)
Ta có: \(20\,d{m^2} = \dfrac{{20}}{{100}}{m^2}\)
Cho biểu thức \(C = \dfrac{{11}}{{2n + 1}}\) . Tìm tất cả các giá trị của $n$ nguyên để giá trị của $C$ là một số tự nhiên.
\(n \in \left\{ { - 6; - 1;0;5} \right\}\)
\(n \in \left\{ { - 1;5} \right\}\)
\(n \in \left\{ {0;5} \right\}\)
\(n \in \left\{ {1;11} \right\}\)
Đáp án : C
- $C$ là số tự nhiên suy ra \(C\) là số nguyên hay $2n + 1$ là ước của $11$ - Từ đó tìm các giá trị của $n$ rồi thử lại kiểm tra lại điều kiện \(C\) là số tự nhiên.
Vì \(C \in N\) nên \(\frac{11}{2n+1} \in N.\)
Để \(\frac{11}{2n+1} \in N\) thì \(11 \vdots (2n+1)\) và \((2n+1) > 0\) hay \((2n+1) \in \left\{ { 1; 11} \right\}\)
Ta có bảng:

Vì \(C \in N\) nên ta nhận các giá trị \(n = 0;n = 5\)
Có bao nhiêu giá trị nguyên dương của \(n\) để \(\dfrac{9}{{4n + 1}}\) đạt giá trị nguyên.
\(1\)
\(0\)
\(2\)
\(3\)
Đáp án : A
Phân số \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\) là một số nguyên nếu \(b\) là ước của $a$
Vì \(n\) nguyên dương nên để \(\dfrac{9}{{4n + 1}}\) nguyên thì \(4n + 1 \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)
Ta có bảng:
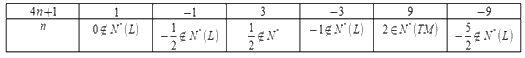
Vậy có duy nhất một giá trị của \(n\) thỏa mãn là \(n = 2\)
Cho các phân số: \(\dfrac{{15}}{{60}};\dfrac{{ - 7}}{5};\dfrac{6}{{15}};\dfrac{{28}}{{ - 20}};\dfrac{3}{{12}}\)
Số cặp phân số bằng nhau trong những phân số trên là:
\(4\)
\(1\)
\(3\)
\(2\)
Đáp án : D
- Ta sẽ chia các phân số thành \(2\) loại: phân số dương, phân số âm (chú ý phân số dương và phân số âm không thể bằng nhau)
- Tìm các cặp phân số bằng nhau trong những phân số dương và các cặp phân số bằng nhau trong những phân số âm rồi kết luận.
Sử dụng kiến thức:
- Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
- Định nghĩa các phân số dương, phân số âm:
+ Phân số âm: là phân số có tử và mẫu là các số nguyên trái dấu.
+ Phân số dương: là phân số có tử và mẫu là các số nguyên cùng dấu.
- Các phân số dương: \(\dfrac{{15}}{{60}};\dfrac{6}{{15}};\dfrac{3}{{12}}\)
+ Vì \(15.15 \ne 60.6\) nên \(\dfrac{{15}}{{60}} \ne \dfrac{6}{{15}}\)
+ Vì \(6.12 \ne 15.3\) nên \(\dfrac{6}{{15}} \ne \dfrac{3}{{12}}\)
+ Vì \(15.12 = 60.3\) nên \(\dfrac{{15}}{{60}} = \dfrac{3}{{12}}\)
- Các phân số âm: \(\dfrac{{ - 7}}{5};\dfrac{{28}}{{ - 20}}\)
Vì \(\left( { - 7} \right).\left( { - 20} \right) = 5.28\) nên \(\dfrac{{ - 7}}{5} = \dfrac{{28}}{{ - 20}}\)
Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.
Tính tổng các giá trị \(x \in Z\) biết rằng \( - \dfrac{{111}}{{37}} < x < \dfrac{{91}}{{13}}.\)
\(22\)
\(20\)
\(18\)
\(15\)
Đáp án : C
Tính giá trị các phân số rồi tìm các số nguyên \(x\) thỏa mãn.
Ta có: \(- \dfrac{{111}}{{37}} < x < \dfrac{{91}}{{13}}\)
Mà \( - \dfrac{{111}}{{37}} < -3; 7 < \dfrac{{91}}{{13}}\)
\(\begin{array}{l} \Rightarrow - 3 < x < 7\\ \Rightarrow x \in \left\{ { - 2; - 1;0;1;2;3;4;5;6} \right\}\end{array}\)
Vậy tổng các giá trị của \(x\) thỏa mãn là: \(\left( { - 2} \right) + \left( { - 1} \right) + ... + 5 + 6 = 18\)
Tìm tập hợp các số nguyên \(n\) để \(A = \dfrac{{3n - 5}}{{n + 4}}\) có giá trị là số nguyên.
\(n \in \left\{ {13} \right\}\)
\(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
\(n \in \left\{ { - 17; - 1;1;17} \right\}\)
\(n \in \left\{ { - 13; - 3;3;13} \right\}\)
Đáp án : B
- Biến đổi \(A\) về dạng \(A = a + \dfrac{b}{{n + 4}}\) với \(a,b \in Z\)
- Để \(A\) nguyên thì \(n + 4 \in U\left( b \right)\)
Ta có:
\(A = \dfrac{{3n - 5}}{{n + 4}} = \dfrac{{3n + 12 - 12 - 5}}{{n + 4}}\)\( = \dfrac{{3\left( {n + 4} \right) + \left( { - 17} \right)}}{{n + 4}}\) \( = \dfrac{{3\left( {n + 4} \right)}}{{n + 4}} + \dfrac{{ - 17}}{{n + 4}} = 3 + \dfrac{{ - 17}}{{n + 4}}\)
Vì \(n \in Z\) nên để \(A \in Z\) thì \(n + 4 \in U\left( { - 17} \right) = \left\{ { \pm 1; \pm 17} \right\}\)
Ta có bảng:

Vậy \(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(\dfrac{x}{5} = \dfrac{3}{y}\) và \(x > y?\)
\(4\)
\(3\)
\(2\)
\(1\)
Đáp án : A
Sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Ta có: \(\dfrac{x}{5} = \dfrac{3}{y}\)\( \Rightarrow x.y = 5.3 = 15\)
Mà \(15 = 5.3 = 15.1 = \left( { - 3} \right).\left( { - 5} \right) = \left( { - 1} \right).\left( { - 15} \right)\) và \(x,y \in Z,x > y\) nên \(\left( {x;y} \right) \in \left\{ {\left( {5;3} \right),\left( {15;1} \right),\left( { - 3; - 5} \right),\left( { - 1; - 15} \right)} \right\}\)
Tìm \(x;y\) biết \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) và \(x - y = 5.\)
\(x = 15;y = 5\)
\(x = 5;y = 15\)
\(x = 20;y = 15\)
\(x = 25;y = 10\)
Đáp án : C
- Rút \(x\) theo \(y\) từ điều kiện đơn giản rồi thay vào đẳng thức hai phân số bằng nhau.
- Sử dụng kiến thức hai phân số bằng nhau để tìm \(y,\) từ đó suy ra \(x\)
- Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Ta có: \(x - y = 5 \Rightarrow x = y + 5\) thay vào \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) ta được:
\(\begin{array}{l}\dfrac{{y + 5 - 4}}{{y - 3}} = \dfrac{4}{3}\\\dfrac{{y + 1}}{{y - 3}} = \dfrac{4}{3}\\3\left( {y + 1} \right) = 4\left( {y - 3} \right)\\3y + 3 = 4y - 12\\3y - 4y = - 12 - 3\\ - y = - 15\\y = 15\\ \Rightarrow x = 15 + 5 = 20\end{array}\)
Vậy \(x = 20;y = 15\)
Tìm số nguyên \(x\) biết rằng \(\dfrac{x}{3} = \dfrac{{27}}{x}\) và \(x < 0.\)
\(x = 81\)
\(x = - 81\)
\(x = - 9\)
\(x = 9\)
Đáp án : C
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau).
\(\begin{array}{l}\dfrac{x}{3} = \dfrac{{27}}{x}\\x.x = 81\\{x^2} = 81\end{array}\)
Ta có: \(x = 9\) hoặc \(x = - 9\)
Kết hợp điều kiện \(x < 0\) nên có một giá trị \(x\) thỏa mãn là: \(x = - 9\)
Viết số nguyên \(a\) dưới dạng phân số ta được:
\(\dfrac{a}{0}\)
\(\dfrac{0}{a}\)
\(\dfrac{a}{1}\)
\(\dfrac{1}{a}\)
Đáp án : C
Viết số nguyên \(a\) dưới dạng phân số ta được: \(\dfrac{a}{1}\).
Cách viết nào sau đây cho ta một phân số:
\(\dfrac{4}{0}\)
\(\dfrac{{1,5}}{3}\)
\(\dfrac{0}{7}\)
\(\dfrac{{ - 5}}{{3,5}}\)
Đáp án : C
+ \(\dfrac{4}{0}\) có mẫu bằng \(0\) nên không là phân số
+ \(\dfrac{{1,5}}{3}\) có \(1,5 \notin \mathbb{Z}\) nên không là phân số
+ \(\dfrac{0}{7}\) là phân số
+ \(\dfrac{{ - 5}}{{3,5}}\) có \(3,5 \notin \mathbb{Z}\) nên không là phân số
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là:
Chín phần bảy
Âm bảy phần chín
Bảy phần chín
Âm chín phần bảy
Đáp án : D
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là: Âm chín phần bảy
Phân số là một khái niệm cơ bản trong toán học, được học từ những năm đầu cấp học. Tuy nhiên, để nắm vững kiến thức về phân số, học sinh cần hiểu rõ các khái niệm mở rộng, đặc biệt là các dạng toán liên quan đến phân số bằng nhau. Bài viết này sẽ cung cấp một cái nhìn tổng quan về các dạng toán này, cùng với các bài tập trắc nghiệm giúp học sinh ôn luyện và củng cố kiến thức.
Trong chương trình Toán 6 Kết nối tri thức, khái niệm phân số được mở rộng so với các lớp tiểu học. Học sinh không chỉ học về phân số dương mà còn làm quen với phân số âm. Điều này đòi hỏi học sinh phải hiểu rõ về số nguyên âm và cách biểu diễn chúng dưới dạng phân số.
Phân số bằng nhau là các phân số biểu diễn cùng một lượng. Để nhận biết hai phân số bằng nhau, ta có thể sử dụng các phương pháp sau:
Dưới đây là một số dạng bài tập trắc nghiệm thường gặp về các dạng toán về mở rộng khái niệm phân số và phân số bằng nhau:
Ví dụ 1: So sánh hai phân số -2/3 và 1/2.
Giải: Ta quy đồng mẫu số hai phân số: -2/3 = -4/6 và 1/2 = 3/6. Vì -4 < 3 nên -2/3 < 1/2.
Ví dụ 2: Rút gọn phân số 12/18.
Giải: ƯCLN(12, 18) = 6. Vậy 12/18 = (12:6)/(18:6) = 2/3.
Để nắm vững kiến thức về các dạng toán về mở rộng khái niệm phân số và phân số bằng nhau, học sinh cần luyện tập thường xuyên. Giaitoan.edu.vn cung cấp một hệ thống bài tập trắc nghiệm đa dạng, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hãy truy cập giaitoan.edu.vn để bắt đầu luyện tập ngay hôm nay!
Việc hiểu rõ các khái niệm mở rộng về phân số và các dạng toán liên quan đến phân số bằng nhau là rất quan trọng đối với học sinh lớp 6. Hy vọng bài viết này đã cung cấp cho học sinh những kiến thức hữu ích và giúp học sinh tự tin hơn trong việc giải các bài toán về phân số.