Chào mừng các em học sinh đến với bài trắc nghiệm Bài 43: Xác suất thực nghiệm môn Toán lớp 6 chương trình Kết nối tri thức. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức đã học về xác suất thực nghiệm.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, bám sát sách giáo khoa, có đáp án chi tiết để các em tự đánh giá năng lực và chuẩn bị tốt nhất cho các bài kiểm tra.
Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng
0,15
0,3
0,6
0,36
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Lần 1 | Số 3 | Lần 6 | Số 5 | Lần 11 | Số 3 | Lần 16 | Số 2 | Lần 21 | Số 1 |
Lần 2 | Số 1 | Lần 7 | Số 2 | Lần 12 | Số 2 | Lần 17 | Số 1 | Lần 22 | Số 5 |
Lần 3 | Số 2 | Lần 8 | Số 3 | Lần 13 | Số 2 | Lần 18 | Số 2 | Lần 23 | Số 3 |
Lần 4 | Số 3 | Lần 9 | Số 4 | Lần 14 | Số 1 | Lần 19 | Số 3 | Lần 24 | Số 4 |
Lần 5 | Số 4 | Lần 10 | Số 5 | Lần 15 | Số 5 | Lần 20 | Số 5 | Lần 25 | Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
0,4
0,14
0,16
0, 25
Xuất hiện số 2
0,42
0,24
0,12
0,6
Xuất hiện số chẵn
0,24
0,63
0,36
0,9
Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
\(\dfrac{2}{5}\)
\(\dfrac{1}{5}\)
\(\dfrac{3}{5}\)
\(\dfrac{3}{4}\)
Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
\(\dfrac{7}{{11}}\)
\(\dfrac{4}{{11}}\)
\(\dfrac{4}{7}\)
\(\dfrac{3}{7}\)
Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
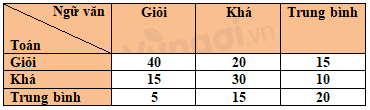
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa
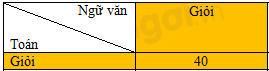
Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Môn Toán đạt loại giỏi
\(\dfrac{{15}}{{34}}\)
\(\dfrac{4}{{17}}\)
\(\dfrac{6}{{17}}\)
\(\dfrac{{13}}{{34}}\)
Loại khá trở lên ở cả hai môn
\(\dfrac{9}{{17}}\)
\(\dfrac{7}{{17}}\)
\(\dfrac{{21}}{{34}}\)
\(\dfrac{7}{{34}}\)
Loại trung bình ở ít nhất một môn
\(\dfrac{{13}}{{17}}\)
\(\dfrac{{13}}{{34}}\)
\(\dfrac{{21}}{{34}}\)
\(\dfrac{1}{2}\)

Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
Khối | Số học sinh được kiểm tra | Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
6 | 210 | 14 |
7 | 200 | 30 |
8 | 180 | 40 |
9 | 170 | 51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm ta được bảng sau:
Quý | Số ca xét nghiệm | Số ca dương tính |
I | 210 | 21 |
II | 150 | 15 |
III | 180 | 9 |
IV | 240 | 48 |
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là
\(0,05\)
\(0,15\)
\(\dfrac{1}{{12}}\)
\(\dfrac{1}{{15}}\)
Có bao nhiêu quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1?
1
2
3
0
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là
0,1
0,25
0,15
0,125
Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:
Màu bút | Bút xanh | Bút vàng | Bút đỏ |
Số lần | 14 | 10 | 16 |
Tính xác suất thực nghiệm của sự kiện lấy được màu đỏ
0,16
0,6
0,4
0,45
Tính xác suất thực nghiệm của sự kiện không lấy được màu vàng
0,25
0,75
0,1
0,9
Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:
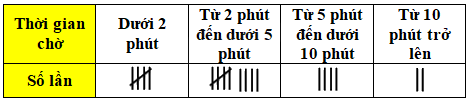
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút”
0,2
5
0,5
0,25
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên”
0,3
6
0,6
0,2
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”
0,1
0,2
0,9
0,5
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
Số lần | 8 | 7 | 3 | 12 | 10 | 10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
0,21
0,44
0,42
0,18
Tung hai đồng xu cân đối 50 lần ta được kết quả như sau:
Sự kiện | Hai đồng sấp | Một đồng sấp, một đồng ngửa | Hai đồng ngửa |
Số lần | 22 | 20 | 8 |
Xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” là
0,2
0,4
0,44
0,16
Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp”
0,22
0,4
0,44
0,16
Lời giải và đáp án
Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng
0,15
0,3
0,6
0,36
Đáp án : B
- Xác định số lần xuất hiện mặt 3 chấm.
- Xác suất thực nghiệm=Số lần xuất hiện mặt 3 chấm: Tổng số lần gieo
Tổng số lần gieo là 20, số lần xuất hiện mặt 3 chấm là 6 lần.
Xác suất thực nghiệm xuất hiện mặt 3 chấm bằng \(\dfrac{6}{{20}} = 0,3\).
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Lần 1 | Số 3 | Lần 6 | Số 5 | Lần 11 | Số 3 | Lần 16 | Số 2 | Lần 21 | Số 1 |
Lần 2 | Số 1 | Lần 7 | Số 2 | Lần 12 | Số 2 | Lần 17 | Số 1 | Lần 22 | Số 5 |
Lần 3 | Số 2 | Lần 8 | Số 3 | Lần 13 | Số 2 | Lần 18 | Số 2 | Lần 23 | Số 3 |
Lần 4 | Số 3 | Lần 9 | Số 4 | Lần 14 | Số 1 | Lần 19 | Số 3 | Lần 24 | Số 4 |
Lần 5 | Số 4 | Lần 10 | Số 5 | Lần 15 | Số 5 | Lần 20 | Số 5 | Lần 25 | Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
0,4
0,14
0,16
0, 25
Đáp án: C
- Đếm số lần có số 1 xuất hiện.
- Xác suất thực nghiệm=Số lần xuất hiện số 1: Tổng số lần rút
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 1 là 4 lần.
Xác suất thực nghiệm xuất hiện số 1 là \(\dfrac{4}{{25}} = 0,16\)
Xuất hiện số 2
0,42
0,24
0,12
0,6
Đáp án: B
- Đếm số lần có số 2 xuất hiện.
- Xác suất thực nghiệm=Số lần xuất hiện số 2: Tổng số lần rút
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 2 là 6 lần.
Xác suất thực nghiệm xuất hiện số 2 là \(\dfrac{6}{{25}} = 0,24\)
Xuất hiện số chẵn
0,24
0,63
0,36
0,9
Đáp án: C
- Đếm số lần có số chẵn xuất hiện: Số 2 + Số 4
- Xác suất thực nghiệm=Số lần xuất hiện số chẵn: Tổng số lần rút
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 2 là 6 lần.
Số lần xuất hiện số 4 là 3 lần.
Số lần xuất hiện số chẵn là 6+3=9 lần.
Xác suất thực nghiệm xuất hiện số 2 là \(\dfrac{9}{{25}} = 0,36\)
Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
\(\dfrac{2}{5}\)
\(\dfrac{1}{5}\)
\(\dfrac{3}{5}\)
\(\dfrac{3}{4}\)
Đáp án : C
- Xác định tổng số lần gieo và số lần gieo được mặt S.
- Xác suất thực nghiệm= Số lần được mặt S: Tổng số lần gieo
Tổng số lần gieo là 30.
Số lần gieo được mặt S là 30-12=18.
Xác suất thực nghiệm xuất hiện mặt S là: \(\dfrac{{18}}{{30}} = \dfrac{3}{5}\)
Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
\(\dfrac{7}{{11}}\)
\(\dfrac{4}{{11}}\)
\(\dfrac{4}{7}\)
\(\dfrac{3}{7}\)
Đáp án : A
- Xác định tổng số lần gieo và số lần gieo được mặt N.
- Xác suất thực nghiệm= Số lần được mặt N: Tổng số lần gieo
Tổng số lần gieo là 22.
Số lần gieo được mặt N là 14.
Xác suất thực nghiệm xuất hiện mặt N là: \(\dfrac{{14}}{{22}} = \dfrac{7}{{11}}\)
Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
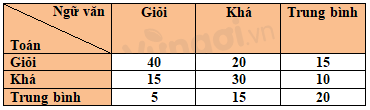
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa
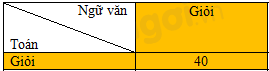
Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Môn Toán đạt loại giỏi
\(\dfrac{{15}}{{34}}\)
\(\dfrac{4}{{17}}\)
\(\dfrac{6}{{17}}\)
\(\dfrac{{13}}{{34}}\)
Đáp án: A
- Tính tổng số học sinh được lựa chọn.
- Tính số học sinh được loại giỏi môn Toán.
- Xác suất thực nghiệm=Số học sinh được loại giỏi môn Toán:Tổng số học sinh được lựa chọn.
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Số học sinh được loại giỏi môn Toán là 40+20+15=75
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại giỏi môn Toán là \(\dfrac{{75}}{{170}} = \dfrac{{15}}{{34}}\)
Loại khá trở lên ở cả hai môn
\(\dfrac{9}{{17}}\)
\(\dfrac{7}{{17}}\)
\(\dfrac{{21}}{{34}}\)
\(\dfrac{7}{{34}}\)
Đáp án: C
- Tính tổng số học sinh được lựa chọn.
- Tính số học sinh loại khá trở lên ở cả 2 môn.
- Xác suất thực nghiệm=Số học sinh được loại khá trở lên ở cả 2 môn:Tổng số học sinh được lựa chọn.
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Các học sinh được loại khá trở lên ở cả 2 môn:
+ Toán giỏi, Ngữ văn giỏi: 40
+ Toán giỏi, Ngữ văn khá: 20
+ Toán khá, Ngữ văn giỏi: 15
+ Toán khá, Ngữ văn khá: 30
Số học sinh được loại khá trở lên ở cả 2 môn là:
40+20+15+30=105
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn là \(\dfrac{{105}}{{170}} = \dfrac{{21}}{{34}}\)
Loại trung bình ở ít nhất một môn
\(\dfrac{{13}}{{17}}\)
\(\dfrac{{13}}{{34}}\)
\(\dfrac{{21}}{{34}}\)
\(\dfrac{1}{2}\)
Đáp án: B
- Xét các trường hợp loại trung bình ở ít nhất một môn.
- Tính số học sinh được loại trung bình ở ít nhất một môn.
- Xác suất thực nghiệm=Số học sinh bị loại trung bình ở ít nhất 1 môn: Tổng số học sinh.
Tổng số học sinh là 170.
Các học sinh được loại trung bình ở ít nhất một môn là:
+ Toán trung bình, Văn giỏi: 5
+ Toán trung bình, Văn khá: 15
+ Toán trung bình, Văn trung bình: 20
+ Văn trung bình, Toán giỏi: 15
+ Văn trung bình, Toán khá: 10
Số học sinh được loại trung bình ở ít nhất một môn là:
5+15+20+15+10=65
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả được loại trung bình ít nhất một môn:
\(\dfrac{{65}}{{170}} = \dfrac{{13}}{{34}}\).

Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
Khối | Số học sinh được kiểm tra | Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
6 | 210 | 14 |
7 | 200 | 30 |
8 | 180 | 40 |
9 | 170 | 51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
- Tính xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” từng khối.
Xác suất thực nghiệm=Số học sinh bị khúc xạ: Số học sinh được kiểm tra.
- So sánh các phân số với nhau.
Số học sinh bị khúc xạ khối 6 là 14. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là \(\dfrac{{14}}{{210}} = \dfrac{1}{{15}}\)
Số học sinh bị khúc xạ khối 7 là 30. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 7 là \(\dfrac{{30}}{{200}} = \dfrac{3}{{20}}\)
Số học sinh bị khúc xạ khối 8 là 40. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 8 là \(\dfrac{{40}}{{180}} = \dfrac{2}{9}\)
Số học sinh bị khúc xạ khối 9 là 51. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 9 là \(\dfrac{{51}}{{170}} = \dfrac{3}{{10}}\)
Số lớn nhất trong các số \(\dfrac{1}{{15}};\dfrac{3}{{20}};\dfrac{2}{9};\dfrac{3}{{10}}\) là \(\dfrac{3}{{10}}\).
Vậy khối có xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối 9
Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm ta được bảng sau:
Quý | Số ca xét nghiệm | Số ca dương tính |
I | 210 | 21 |
II | 150 | 15 |
III | 180 | 9 |
IV | 240 | 48 |
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là
\(0,05\)
\(0,15\)
\(\dfrac{1}{{12}}\)
\(\dfrac{1}{{15}}\)
Đáp án: C
- Tính số ca xét nghiệm sau quý III tính từ đầu năm.
- Tính số ca dương tính sau quý III tính từ đầu năm.
- Xác suất thực nghiệm=Số ca dương tính: Số ca xét nghiệm.
Số ca xét nghiệm sau quý III tính từ đầu năm là 210+150+180=540.
Số ca dương tính sau quý III tính từ đầu năm là 21+15+9=45.
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là \(\dfrac{{45}}{{540}} = \dfrac{1}{{12}}\)
Có bao nhiêu quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1?
1
2
3
0
Đáp án: A
Bước 1: Tính xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của từng quý:
- Xác định số ca dương tính quý I, II, III, IV.
- Xác suất thực nghiệm=Số ca dương tính:Số ca xét nghiệm.
Bước 2: So sánh với 0,1.
Bước 1:
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý I là \(\dfrac{{21}}{{210}} = 0,1\)
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý II là \(\dfrac{{15}}{{150}} = 0,1\)
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý III là \(\dfrac{9}{{180}} = 0,05\)
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý IV là \(\dfrac{{48}}{{240}} = 0,2\)
Bước 2:
Ta có một số nhỏ hơn 0,1 là 0,05.
Vậy có 1 quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1.
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là
0,1
0,25
0,15
0,125
Đáp án: A
- Xác định số ca dương tính quý I.
- Xác suất thực nghiệm=Số ca dương tính:Số ca xét nghiệm.
Số ca xét nghiệm quý I là 210.
Số ca dương tính là 21 ca.
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là
\(\dfrac{{21}}{{210}} = 0,1\)
Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:
Màu bút | Bút xanh | Bút vàng | Bút đỏ |
Số lần | 14 | 10 | 16 |
Tính xác suất thực nghiệm của sự kiện lấy được màu đỏ
0,16
0,6
0,4
0,45
Đáp án: C
- Xác định số lần lấy được màu đỏ.
- Tính xác suất thực nghiệm=Số lần lấy được màu đỏ:40
Tổng số lần lấy là 40.
Số lần lấy được màu đỏ là 16.
Xác suất thực nghiệm của sự kiện lấy được màu đỏ là:
\(\dfrac{{16}}{{40}} = 0,4\)
Tính xác suất thực nghiệm của sự kiện không lấy được màu vàng
0,25
0,75
0,1
0,9
Đáp án: B
- Xác định số lần lấy được màu vàng.
- Xác định số lần không lấy được màu vàng.
- Tính xác suất thực nghiệm=Số lần không lấy được màu vàng:40
Tổng số lần lấy bút là 40.
Số lần lấy được màu vàng là 10
Số lần không lấy được màu vàng là 40-10=30.
Xác suất suất thực nghiệm của sự kiện không lấy được màu vàng là:
\(\dfrac{{30}}{{40}} = 0,75\)
Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:
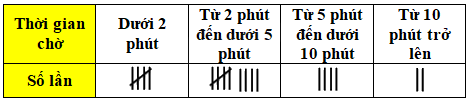
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút”
0,2
5
0,5
0,25
Đáp án: D
- Một gạch là 1 lần (Tính cả gạch chéo).
- Xác định số lần Sơn phải chờ xe dưới 2 phút.
- Tính xác suất:

Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút” là:
\(\dfrac{5}{{20}} = 0,25\)
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên”
0,3
6
0,6
0,2
Đáp án: A
- Xác định số lần Sơn phải chờ xe từ 5 phút trở lên: Từ 5 phút đến dưới 10 phút + Từ 10 phút trở lên.
- Tính xác suất:

Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là: 4 lần
Số lần Sơn phải chờ xe từ 10 phút trở lên là: 2 lần
Số lần Sơn phải chờ xe từ 5 phút trở lên là: 4+2 = 6 lần.
Xác suất của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là:
\(\dfrac{6}{{20}} = 0,3\)
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”
0,1
0,2
0,9
0,5
Đáp án: C
- Xác định số lần Sơn phải chờ xe dưới 10 phút: dưới 2 phút + Từ 2 đến dưới 5 phút + Từ 5 phút đến dưới 10 phút .
- Tính xác suất:

Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.
Số lần Sơn phải chờ xe từ 2 phút đến dưới 5 phút là 9 lần.
Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là 4 lần.
Số lần Sơn phải chờ xe dưới 10 phút là 5+9+4=18 lần.
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút” là:
\(\dfrac{{18}}{{20}} = 0,9\)
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
Số lần | 8 | 7 | 3 | 12 | 10 | 10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
0,21
0,44
0,42
0,18
Đáp án : C
- Xác định các mặt có số lẻ chấm
- Tìm trên bảng số lần xuất hiện của các mặt đó.
- Tính xác suất thực nghiệm:

Tổng số lần gieo là 50.
Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.
Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.
Số lần được mặt có số lẻ chấm là 8+3+10=21 lần
Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:
\(\dfrac{{21}}{{50}} = 0,42\)
Tung hai đồng xu cân đối 50 lần ta được kết quả như sau:
Sự kiện | Hai đồng sấp | Một đồng sấp, một đồng ngửa | Hai đồng ngửa |
Số lần | 22 | 20 | 8 |
Xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” là
0,2
0,4
0,44
0,16
Đáp án: B
- Xác định số lần sự kiện xảy ra.
- Xác suất thực nghiệm=Số lần sự kiện xảy ra:50.
- Số lần tung là 50.
- Số lần sự kiện “Có một đồng xu sấp, một đồng xu ngửa” xảy ra là 20.
- Xác suất thực nghiệm của sự kiện trên là
\(20:50 = 0,4\)
Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp”
0,22
0,4
0,44
0,16
Đáp án: C
- Xác định số lần sự kiện xảy ra.
- Xác suất thực nghiệm=Số lần sự kiện xảy ra:50.
- Số lần tung là 50.
- Số lần sự kiện “Hai đồng xu đều sấp” xảy ra là 22.
- Xác suất thực nghiệm của sự kiện trên là là $22:50=0,44$.
Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng
0,15
0,3
0,6
0,36
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Lần 1 | Số 3 | Lần 6 | Số 5 | Lần 11 | Số 3 | Lần 16 | Số 2 | Lần 21 | Số 1 |
Lần 2 | Số 1 | Lần 7 | Số 2 | Lần 12 | Số 2 | Lần 17 | Số 1 | Lần 22 | Số 5 |
Lần 3 | Số 2 | Lần 8 | Số 3 | Lần 13 | Số 2 | Lần 18 | Số 2 | Lần 23 | Số 3 |
Lần 4 | Số 3 | Lần 9 | Số 4 | Lần 14 | Số 1 | Lần 19 | Số 3 | Lần 24 | Số 4 |
Lần 5 | Số 4 | Lần 10 | Số 5 | Lần 15 | Số 5 | Lần 20 | Số 5 | Lần 25 | Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
0,4
0,14
0,16
0, 25
Xuất hiện số 2
0,42
0,24
0,12
0,6
Xuất hiện số chẵn
0,24
0,63
0,36
0,9
Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
\(\dfrac{2}{5}\)
\(\dfrac{1}{5}\)
\(\dfrac{3}{5}\)
\(\dfrac{3}{4}\)
Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
\(\dfrac{7}{{11}}\)
\(\dfrac{4}{{11}}\)
\(\dfrac{4}{7}\)
\(\dfrac{3}{7}\)
Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:

Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa

Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Môn Toán đạt loại giỏi
\(\dfrac{{15}}{{34}}\)
\(\dfrac{4}{{17}}\)
\(\dfrac{6}{{17}}\)
\(\dfrac{{13}}{{34}}\)
Loại khá trở lên ở cả hai môn
\(\dfrac{9}{{17}}\)
\(\dfrac{7}{{17}}\)
\(\dfrac{{21}}{{34}}\)
\(\dfrac{7}{{34}}\)
Loại trung bình ở ít nhất một môn
\(\dfrac{{13}}{{17}}\)
\(\dfrac{{13}}{{34}}\)
\(\dfrac{{21}}{{34}}\)
\(\dfrac{1}{2}\)

Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
Khối | Số học sinh được kiểm tra | Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
6 | 210 | 14 |
7 | 200 | 30 |
8 | 180 | 40 |
9 | 170 | 51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm ta được bảng sau:
Quý | Số ca xét nghiệm | Số ca dương tính |
I | 210 | 21 |
II | 150 | 15 |
III | 180 | 9 |
IV | 240 | 48 |
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là
\(0,05\)
\(0,15\)
\(\dfrac{1}{{12}}\)
\(\dfrac{1}{{15}}\)
Có bao nhiêu quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1?
1
2
3
0
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là
0,1
0,25
0,15
0,125
Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:
Màu bút | Bút xanh | Bút vàng | Bút đỏ |
Số lần | 14 | 10 | 16 |
Tính xác suất thực nghiệm của sự kiện lấy được màu đỏ
0,16
0,6
0,4
0,45
Tính xác suất thực nghiệm của sự kiện không lấy được màu vàng
0,25
0,75
0,1
0,9
Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút”
0,2
5
0,5
0,25
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên”
0,3
6
0,6
0,2
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”
0,1
0,2
0,9
0,5
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
Số lần | 8 | 7 | 3 | 12 | 10 | 10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
0,21
0,44
0,42
0,18
Tung hai đồng xu cân đối 50 lần ta được kết quả như sau:
Sự kiện | Hai đồng sấp | Một đồng sấp, một đồng ngửa | Hai đồng ngửa |
Số lần | 22 | 20 | 8 |
Xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” là
0,2
0,4
0,44
0,16
Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp”
0,22
0,4
0,44
0,16
Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng
0,15
0,3
0,6
0,36
Đáp án : B
- Xác định số lần xuất hiện mặt 3 chấm.
- Xác suất thực nghiệm=Số lần xuất hiện mặt 3 chấm: Tổng số lần gieo
Tổng số lần gieo là 20, số lần xuất hiện mặt 3 chấm là 6 lần.
Xác suất thực nghiệm xuất hiện mặt 3 chấm bằng \(\dfrac{6}{{20}} = 0,3\).
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Lần 1 | Số 3 | Lần 6 | Số 5 | Lần 11 | Số 3 | Lần 16 | Số 2 | Lần 21 | Số 1 |
Lần 2 | Số 1 | Lần 7 | Số 2 | Lần 12 | Số 2 | Lần 17 | Số 1 | Lần 22 | Số 5 |
Lần 3 | Số 2 | Lần 8 | Số 3 | Lần 13 | Số 2 | Lần 18 | Số 2 | Lần 23 | Số 3 |
Lần 4 | Số 3 | Lần 9 | Số 4 | Lần 14 | Số 1 | Lần 19 | Số 3 | Lần 24 | Số 4 |
Lần 5 | Số 4 | Lần 10 | Số 5 | Lần 15 | Số 5 | Lần 20 | Số 5 | Lần 25 | Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
0,4
0,14
0,16
0, 25
Đáp án: C
- Đếm số lần có số 1 xuất hiện.
- Xác suất thực nghiệm=Số lần xuất hiện số 1: Tổng số lần rút
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 1 là 4 lần.
Xác suất thực nghiệm xuất hiện số 1 là \(\dfrac{4}{{25}} = 0,16\)
Xuất hiện số 2
0,42
0,24
0,12
0,6
Đáp án: B
- Đếm số lần có số 2 xuất hiện.
- Xác suất thực nghiệm=Số lần xuất hiện số 2: Tổng số lần rút
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 2 là 6 lần.
Xác suất thực nghiệm xuất hiện số 2 là \(\dfrac{6}{{25}} = 0,24\)
Xuất hiện số chẵn
0,24
0,63
0,36
0,9
Đáp án: C
- Đếm số lần có số chẵn xuất hiện: Số 2 + Số 4
- Xác suất thực nghiệm=Số lần xuất hiện số chẵn: Tổng số lần rút
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 2 là 6 lần.
Số lần xuất hiện số 4 là 3 lần.
Số lần xuất hiện số chẵn là 6+3=9 lần.
Xác suất thực nghiệm xuất hiện số 2 là \(\dfrac{9}{{25}} = 0,36\)
Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
\(\dfrac{2}{5}\)
\(\dfrac{1}{5}\)
\(\dfrac{3}{5}\)
\(\dfrac{3}{4}\)
Đáp án : C
- Xác định tổng số lần gieo và số lần gieo được mặt S.
- Xác suất thực nghiệm= Số lần được mặt S: Tổng số lần gieo
Tổng số lần gieo là 30.
Số lần gieo được mặt S là 30-12=18.
Xác suất thực nghiệm xuất hiện mặt S là: \(\dfrac{{18}}{{30}} = \dfrac{3}{5}\)
Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
\(\dfrac{7}{{11}}\)
\(\dfrac{4}{{11}}\)
\(\dfrac{4}{7}\)
\(\dfrac{3}{7}\)
Đáp án : A
- Xác định tổng số lần gieo và số lần gieo được mặt N.
- Xác suất thực nghiệm= Số lần được mặt N: Tổng số lần gieo
Tổng số lần gieo là 22.
Số lần gieo được mặt N là 14.
Xác suất thực nghiệm xuất hiện mặt N là: \(\dfrac{{14}}{{22}} = \dfrac{7}{{11}}\)
Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:

Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa

Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Môn Toán đạt loại giỏi
\(\dfrac{{15}}{{34}}\)
\(\dfrac{4}{{17}}\)
\(\dfrac{6}{{17}}\)
\(\dfrac{{13}}{{34}}\)
Đáp án: A
- Tính tổng số học sinh được lựa chọn.
- Tính số học sinh được loại giỏi môn Toán.
- Xác suất thực nghiệm=Số học sinh được loại giỏi môn Toán:Tổng số học sinh được lựa chọn.
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Số học sinh được loại giỏi môn Toán là 40+20+15=75
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại giỏi môn Toán là \(\dfrac{{75}}{{170}} = \dfrac{{15}}{{34}}\)
Loại khá trở lên ở cả hai môn
\(\dfrac{9}{{17}}\)
\(\dfrac{7}{{17}}\)
\(\dfrac{{21}}{{34}}\)
\(\dfrac{7}{{34}}\)
Đáp án: C
- Tính tổng số học sinh được lựa chọn.
- Tính số học sinh loại khá trở lên ở cả 2 môn.
- Xác suất thực nghiệm=Số học sinh được loại khá trở lên ở cả 2 môn:Tổng số học sinh được lựa chọn.
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Các học sinh được loại khá trở lên ở cả 2 môn:
+ Toán giỏi, Ngữ văn giỏi: 40
+ Toán giỏi, Ngữ văn khá: 20
+ Toán khá, Ngữ văn giỏi: 15
+ Toán khá, Ngữ văn khá: 30
Số học sinh được loại khá trở lên ở cả 2 môn là:
40+20+15+30=105
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn là \(\dfrac{{105}}{{170}} = \dfrac{{21}}{{34}}\)
Loại trung bình ở ít nhất một môn
\(\dfrac{{13}}{{17}}\)
\(\dfrac{{13}}{{34}}\)
\(\dfrac{{21}}{{34}}\)
\(\dfrac{1}{2}\)
Đáp án: B
- Xét các trường hợp loại trung bình ở ít nhất một môn.
- Tính số học sinh được loại trung bình ở ít nhất một môn.
- Xác suất thực nghiệm=Số học sinh bị loại trung bình ở ít nhất 1 môn: Tổng số học sinh.
Tổng số học sinh là 170.
Các học sinh được loại trung bình ở ít nhất một môn là:
+ Toán trung bình, Văn giỏi: 5
+ Toán trung bình, Văn khá: 15
+ Toán trung bình, Văn trung bình: 20
+ Văn trung bình, Toán giỏi: 15
+ Văn trung bình, Toán khá: 10
Số học sinh được loại trung bình ở ít nhất một môn là:
5+15+20+15+10=65
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả được loại trung bình ít nhất một môn:
\(\dfrac{{65}}{{170}} = \dfrac{{13}}{{34}}\).

Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
Khối | Số học sinh được kiểm tra | Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
6 | 210 | 14 |
7 | 200 | 30 |
8 | 180 | 40 |
9 | 170 | 51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
- Tính xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” từng khối.
Xác suất thực nghiệm=Số học sinh bị khúc xạ: Số học sinh được kiểm tra.
- So sánh các phân số với nhau.
Số học sinh bị khúc xạ khối 6 là 14. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là \(\dfrac{{14}}{{210}} = \dfrac{1}{{15}}\)
Số học sinh bị khúc xạ khối 7 là 30. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 7 là \(\dfrac{{30}}{{200}} = \dfrac{3}{{20}}\)
Số học sinh bị khúc xạ khối 8 là 40. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 8 là \(\dfrac{{40}}{{180}} = \dfrac{2}{9}\)
Số học sinh bị khúc xạ khối 9 là 51. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 9 là \(\dfrac{{51}}{{170}} = \dfrac{3}{{10}}\)
Số lớn nhất trong các số \(\dfrac{1}{{15}};\dfrac{3}{{20}};\dfrac{2}{9};\dfrac{3}{{10}}\) là \(\dfrac{3}{{10}}\).
Vậy khối có xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối 9
Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm ta được bảng sau:
Quý | Số ca xét nghiệm | Số ca dương tính |
I | 210 | 21 |
II | 150 | 15 |
III | 180 | 9 |
IV | 240 | 48 |
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là
\(0,05\)
\(0,15\)
\(\dfrac{1}{{12}}\)
\(\dfrac{1}{{15}}\)
Đáp án: C
- Tính số ca xét nghiệm sau quý III tính từ đầu năm.
- Tính số ca dương tính sau quý III tính từ đầu năm.
- Xác suất thực nghiệm=Số ca dương tính: Số ca xét nghiệm.
Số ca xét nghiệm sau quý III tính từ đầu năm là 210+150+180=540.
Số ca dương tính sau quý III tính từ đầu năm là 21+15+9=45.
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là \(\dfrac{{45}}{{540}} = \dfrac{1}{{12}}\)
Có bao nhiêu quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1?
1
2
3
0
Đáp án: A
Bước 1: Tính xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của từng quý:
- Xác định số ca dương tính quý I, II, III, IV.
- Xác suất thực nghiệm=Số ca dương tính:Số ca xét nghiệm.
Bước 2: So sánh với 0,1.
Bước 1:
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý I là \(\dfrac{{21}}{{210}} = 0,1\)
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý II là \(\dfrac{{15}}{{150}} = 0,1\)
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý III là \(\dfrac{9}{{180}} = 0,05\)
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý IV là \(\dfrac{{48}}{{240}} = 0,2\)
Bước 2:
Ta có một số nhỏ hơn 0,1 là 0,05.
Vậy có 1 quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1.
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là
0,1
0,25
0,15
0,125
Đáp án: A
- Xác định số ca dương tính quý I.
- Xác suất thực nghiệm=Số ca dương tính:Số ca xét nghiệm.
Số ca xét nghiệm quý I là 210.
Số ca dương tính là 21 ca.
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là
\(\dfrac{{21}}{{210}} = 0,1\)
Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:
Màu bút | Bút xanh | Bút vàng | Bút đỏ |
Số lần | 14 | 10 | 16 |
Tính xác suất thực nghiệm của sự kiện lấy được màu đỏ
0,16
0,6
0,4
0,45
Đáp án: C
- Xác định số lần lấy được màu đỏ.
- Tính xác suất thực nghiệm=Số lần lấy được màu đỏ:40
Tổng số lần lấy là 40.
Số lần lấy được màu đỏ là 16.
Xác suất thực nghiệm của sự kiện lấy được màu đỏ là:
\(\dfrac{{16}}{{40}} = 0,4\)
Tính xác suất thực nghiệm của sự kiện không lấy được màu vàng
0,25
0,75
0,1
0,9
Đáp án: B
- Xác định số lần lấy được màu vàng.
- Xác định số lần không lấy được màu vàng.
- Tính xác suất thực nghiệm=Số lần không lấy được màu vàng:40
Tổng số lần lấy bút là 40.
Số lần lấy được màu vàng là 10
Số lần không lấy được màu vàng là 40-10=30.
Xác suất suất thực nghiệm của sự kiện không lấy được màu vàng là:
\(\dfrac{{30}}{{40}} = 0,75\)
Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút”
0,2
5
0,5
0,25
Đáp án: D
- Một gạch là 1 lần (Tính cả gạch chéo).
- Xác định số lần Sơn phải chờ xe dưới 2 phút.
- Tính xác suất:

Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút” là:
\(\dfrac{5}{{20}} = 0,25\)
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên”
0,3
6
0,6
0,2
Đáp án: A
- Xác định số lần Sơn phải chờ xe từ 5 phút trở lên: Từ 5 phút đến dưới 10 phút + Từ 10 phút trở lên.
- Tính xác suất:

Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là: 4 lần
Số lần Sơn phải chờ xe từ 10 phút trở lên là: 2 lần
Số lần Sơn phải chờ xe từ 5 phút trở lên là: 4+2 = 6 lần.
Xác suất của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là:
\(\dfrac{6}{{20}} = 0,3\)
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”
0,1
0,2
0,9
0,5
Đáp án: C
- Xác định số lần Sơn phải chờ xe dưới 10 phút: dưới 2 phút + Từ 2 đến dưới 5 phút + Từ 5 phút đến dưới 10 phút .
- Tính xác suất:

Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.
Số lần Sơn phải chờ xe từ 2 phút đến dưới 5 phút là 9 lần.
Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là 4 lần.
Số lần Sơn phải chờ xe dưới 10 phút là 5+9+4=18 lần.
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút” là:
\(\dfrac{{18}}{{20}} = 0,9\)
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
Số lần | 8 | 7 | 3 | 12 | 10 | 10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
0,21
0,44
0,42
0,18
Đáp án : C
- Xác định các mặt có số lẻ chấm
- Tìm trên bảng số lần xuất hiện của các mặt đó.
- Tính xác suất thực nghiệm:

Tổng số lần gieo là 50.
Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.
Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.
Số lần được mặt có số lẻ chấm là 8+3+10=21 lần
Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:
\(\dfrac{{21}}{{50}} = 0,42\)
Tung hai đồng xu cân đối 50 lần ta được kết quả như sau:
Sự kiện | Hai đồng sấp | Một đồng sấp, một đồng ngửa | Hai đồng ngửa |
Số lần | 22 | 20 | 8 |
Xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” là
0,2
0,4
0,44
0,16
Đáp án: B
- Xác định số lần sự kiện xảy ra.
- Xác suất thực nghiệm=Số lần sự kiện xảy ra:50.
- Số lần tung là 50.
- Số lần sự kiện “Có một đồng xu sấp, một đồng xu ngửa” xảy ra là 20.
- Xác suất thực nghiệm của sự kiện trên là
\(20:50 = 0,4\)
Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp”
0,22
0,4
0,44
0,16
Đáp án: C
- Xác định số lần sự kiện xảy ra.
- Xác suất thực nghiệm=Số lần sự kiện xảy ra:50.
- Số lần tung là 50.
- Số lần sự kiện “Hai đồng xu đều sấp” xảy ra là 22.
- Xác suất thực nghiệm của sự kiện trên là là $22:50=0,44$.
Bài 43 trong chương trình Toán 6 Kết nối tri thức giới thiệu khái niệm về xác suất thực nghiệm. Đây là một khái niệm quan trọng, giúp học sinh làm quen với việc dự đoán khả năng xảy ra của một sự kiện dựa trên kết quả của các thử nghiệm thực tế.
Xác suất thực nghiệm của một sự kiện là tỉ số giữa số lần sự kiện đó xảy ra và tổng số lần thực hiện thử nghiệm. Công thức tính xác suất thực nghiệm được biểu diễn như sau:
Xác suất thực nghiệm (A) = (Số lần sự kiện A xảy ra) / (Tổng số lần thực hiện thử nghiệm)
Ví dụ: Gieo một con xúc xắc 20 lần, kết quả thống kê được như sau:
Xác suất thực nghiệm của việc xuất hiện mặt 1 là: 3/20 = 0.15
Xác suất thực nghiệm của việc xuất hiện mặt 2 là: 4/20 = 0.2
...
Dưới đây là một số bài tập trắc nghiệm minh họa để giúp các em hiểu rõ hơn về khái niệm xác suất thực nghiệm:
Một hộp có 10 quả bóng, trong đó có 3 quả bóng màu đỏ, 2 quả bóng màu xanh và 5 quả bóng màu trắng. Lấy ngẫu nhiên một quả bóng từ hộp. Tính xác suất thực nghiệm của việc lấy được quả bóng màu đỏ.
Đáp án: B. 0.3
Gieo một đồng xu 50 lần, kết quả thống kê được 28 lần xuất hiện mặt sấp và 22 lần xuất hiện mặt ngửa. Tính xác suất thực nghiệm của việc xuất hiện mặt ngửa.
Đáp án: B. 0.44
Để nắm vững kiến thức về xác suất thực nghiệm, các em nên luyện tập thêm nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú, đa dạng, có đáp án chi tiết để các em tham khảo.
Bài 43: Xác suất thực nghiệm Toán 6 Kết nối tri thức là một bài học quan trọng, giúp học sinh làm quen với khái niệm xác suất và ứng dụng nó vào thực tế. Hy vọng rằng, với những kiến thức và bài tập đã trình bày, các em sẽ hiểu rõ hơn về bài học này và đạt kết quả tốt trong các bài kiểm tra.