Bài viết này cung cấp bộ câu hỏi trắc nghiệm giúp học sinh lớp 6 ôn tập và củng cố kiến thức về bài học "Kết quả có thể và sự kiện trong trò chơi, thí nghiệm" thuộc chương trình Toán 6 Kết nối tri thức.
Các câu hỏi được thiết kế đa dạng, bao gồm nhiều dạng bài tập khác nhau, từ nhận biết đến vận dụng, giúp học sinh hiểu sâu sắc và nắm vững kiến thức.
Hệ thống đáp án chi tiết đi kèm sẽ giúp học sinh tự đánh giá kết quả học tập và rút ra kinh nghiệm.

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là
1. Rút ngẫu nhiên
thẻ;
2. Tập hợp các kết quả có thể xảy ra đối với
xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Viết tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
M={1;2;3;4}
M=(1,2,3,4,5)
M={1,2,3,4}
M={1;2;3;4;5}
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Số xuất hiện trên thẻ được rút có phải là phần tử của tập hợp {1;2;3;4;5} hay không?
Không
Có
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Nêu những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra?
5
1, 2, 3, 4, 5
1, 2, 3
1,2
Cho phép thử nghiệm gieo con xúc xắc 6 mặt. Sự kiện nào trong các sự kiện sau có thể xảy ra:
“Số chấm nhỏ hơn 5”
“Số chấm lớn hơn 6”
“Số chấm bằng 0”
“Số chấm bằng 7”
Phép thử nghiệm: Bạn Ngô chọn một ngày trong tuần để đá bóng. Có tất cả bao nhiêu kết quả có thể xảy ra của phép thử nghiệm này.
5
6
7
4
Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp, hỏi có tất cả bao nhiêu kết quả có thể xảy ra?
1
2
3
4
Trong hộp có 10 lá thư có bì thư giống nhau, bên trong mỗi bì thư có 1 mảnh giấy và được đánh số từ 1 đến 10. Mỗi bạn lấy ngẫu nhiên một bì thư, xem số ghi trên lá thư rồi trả lại vào bì và cho vào hộp. Tập hợp tất cả các kết quả có thể xảy ra là:
\(A = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\)
\(A = \left\{ {10} \right\}\)
\(10\)
\(1\)
Hãy viết tập hợp các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt
\(1;2;3;4;5;6\)
\(Y = 6\)
\(6\)
\(Y = \left\{ {1;2;3;4;5;6} \right\}\)
Tập hợp các kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu là
\(X = \left\{ {N,S} \right\}\)
\(X = \left\{ N \right\}\)
\(X = \left\{ S \right\}\)
\(X = \left\{ {NN,S} \right\}\)
Gieo đồng thời 2 con xúc xắc và nhận được số chấm xuất hiện trên hai con xúc xắc lần lượt là 1 và 5.
Sự kiện nào sau đây xảy ra?
Tổng số chấm xuất hiện trên hai con xúc xắc là số lẻ.
Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 6.
Tổng số chấm xuất hiện trên hai con xúc xắc là số chẵn.
Tổng số chấm xuất hiện trên hai con xúc xắc là bằng 5.
Trong hộp có 10 tấm thẻ ghi các số 2;2;3;3;3;4;5;5;5;5. Yêu cầu 5 bạn lần lượt rút ngẫu nhiên 1 thẻ, quan sát số ghi trên thẻ rồi trả lại thẻ vào hộp. Quân và Hương đã rút được thẻ ghi số lần lượt là 2 và 5.
Có bao nhiêu sự kiện trong các sự kiện sau không xảy ra?
Sự kiện 1: “Có bạn rút được thẻ số 5”
Sự kiện 2: “Cả hai bạn đều rút được thẻ ghi số lẻ”
Sự kiện 3: “Cả hai bạn đều rút được thẻ ghi số nguyên tố”
Sự kiện 4: “Có đúng một bạn rút được thẻ lớn hơn 3”
1
2
3
4
Nga quay tấm bìa và thấy mũi tên chỉ vào ô số 3 như hình bên. Hãy cho biết sự kiện nào sau đây xảy ra
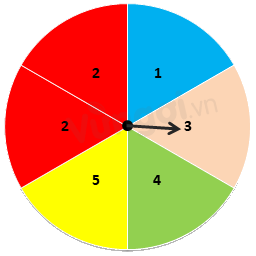
Mũi tên chỉ vào ô ghi số nhỏ hơn 5
Mũi tên chỉ vào ô ghi số 5
Mũi tên chỉ vào ô ghi số lớn hơn 3
Mũi tên chỉ vào ô ghi số chẵn
Lời giải và đáp án

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là
1. Rút ngẫu nhiên
thẻ;
2. Tập hợp các kết quả có thể xảy ra đối với
xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.
1. Rút ngẫu nhiên
thẻ;
2. Tập hợp các kết quả có thể xảy ra đối với
xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.
Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là
1. Rút ngẫu nhiên 1 thẻ;
2. Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1,2,3,4,5 là các số xuất hiện trên thẻ.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Viết tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
M={1;2;3;4}
M=(1,2,3,4,5)
M={1,2,3,4}
M={1;2;3;4;5}
Đáp án : D
- Tìm các kết quả có thể xảy ra.
- Viết tập hợp: Viết các số trong dấu ngoặc kép { }.
Số có thể xuất hiện trên thẻ là một trong năm số: 1;2;3;4;5.
Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ là
M={1;2;3;4;5}.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Số xuất hiện trên thẻ được rút có phải là phần tử của tập hợp {1;2;3;4;5} hay không?
Không
Có
Có
- Tìm các kết quả có thể xảy ra.
- Số có trong tập hợp là phần tử của tập hợp.
Số có thể xuất hiện trên thẻ là một trong năm số: 1;2;3;4;5.
Các số này đều là phần tử của tập hợp {1;2;3;4;5}.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Nêu những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra?
5
1, 2, 3, 4, 5
1, 2, 3
1,2
Đáp án : B
- Tìm các kết quả có thể xảy ra.
Số có thể xuất hiện trên thẻ là một trong năm số: 1;2;3;4;5.
Cho phép thử nghiệm gieo con xúc xắc 6 mặt. Sự kiện nào trong các sự kiện sau có thể xảy ra:
“Số chấm nhỏ hơn 5”
“Số chấm lớn hơn 6”
“Số chấm bằng 0”
“Số chấm bằng 7”
Đáp án : A
Tìm tất các kết quả có thể xảy ra khi gieo xúc xắc.
Kiểm tra sự kiện có thể nằm trong các kết quả đó không.
Các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt là: 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm.
Khi đó số chấm nhỏ hơn 5 có thể xảy ra. Đáp án A đúng.
Số chấm tối đa là 6 nên B sai.
Không có số chấm bằng 0 trong các kết quả có thể xảy ra nên C sai.
Không có số chấm bằng 7 trong các kết quả có thể xảy ra nên D sai.
Phép thử nghiệm: Bạn Ngô chọn một ngày trong tuần để đá bóng. Có tất cả bao nhiêu kết quả có thể xảy ra của phép thử nghiệm này.
5
6
7
4
Đáp án : C
Liệt kê các ngày trong tuần mà Ngô có thể chọn.
Đếm số ngày.
Một tuần có 7 ngày nên Ngô có thể chọn một trong 7 ngày đó để đi đá bóng. Hay số kết quả có thể xảy ra là 7.
Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp, hỏi có tất cả bao nhiêu kết quả có thể xảy ra?
1
2
3
4
Đáp án : B
Tìm tất cả các kết quả có thể xảy ra trong mỗi lần lấy bóng.
Đếm số các kết quả có thể xảy ra.
Các kết quả có thể xảy ra là: (1 xanh + 1 vàng) ; (2 vàng).
Vậy có 2 kết quả có thể xảy ra.
Trong hộp có 10 lá thư có bì thư giống nhau, bên trong mỗi bì thư có 1 mảnh giấy và được đánh số từ 1 đến 10. Mỗi bạn lấy ngẫu nhiên một bì thư, xem số ghi trên lá thư rồi trả lại vào bì và cho vào hộp. Tập hợp tất cả các kết quả có thể xảy ra là:
\(A = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\)
\(A = \left\{ {10} \right\}\)
\(10\)
\(1\)
Đáp án : A
Tìm tất cả các kết quả có thể xảy ra khi lấy ngẫu nhiên.
Viết các kết quả đó trong một tập hợp.
Các số có thể ghi trên lá thư là 1;2;3;4;5;6;7;8;9;10 nên tập hợp tất cả các kết quả có thể xảy ra là \(A = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\)
Hãy viết tập hợp các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt
\(1;2;3;4;5;6\)
\(Y = 6\)
\(6\)
\(Y = \left\{ {1;2;3;4;5;6} \right\}\)
Đáp án : D
Liệt kê các trường hợp của phép thử nghiệm gieo một con xúc xắc 6 mặt.
Viết các kết quả đó trong một tập hợp.
Các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt là: 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm.
Vậy tập hợp cần tìm là \(Y = \left\{ {1;2;3;4;5;6} \right\}\)
Tập hợp các kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu là
\(X = \left\{ {N,S} \right\}\)
\(X = \left\{ N \right\}\)
\(X = \left\{ S \right\}\)
\(X = \left\{ {NN,S} \right\}\)
Đáp án : A
Liệt kê các trường hợp của phép thử nghiệm tung đồng xu.
Phép thử nghiệm tung đồng xu có kết quả có thể là sấp (S) hoặc ngửa (N).
Vậy tập hợp các kết quả có thể xảy ra là \(X = \left\{ {N,S} \right\}\)
Gieo đồng thời 2 con xúc xắc và nhận được số chấm xuất hiện trên hai con xúc xắc lần lượt là 1 và 5.
Sự kiện nào sau đây xảy ra?
Tổng số chấm xuất hiện trên hai con xúc xắc là số lẻ.
Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 6.
Tổng số chấm xuất hiện trên hai con xúc xắc là số chẵn.
Tổng số chấm xuất hiện trên hai con xúc xắc là bằng 5.
Đáp án : C
- Tính tổng số chấm xuất hiện.
- Đối chiếu với đáp án.
Tổng số chấm xuất hiện ở hai con xúc xắc là 1+5=6.
6 là số chẵn nên tổng số chấm xuất hiện trên hai con xúc xắc là số chẵn.
Trong hộp có 10 tấm thẻ ghi các số 2;2;3;3;3;4;5;5;5;5. Yêu cầu 5 bạn lần lượt rút ngẫu nhiên 1 thẻ, quan sát số ghi trên thẻ rồi trả lại thẻ vào hộp. Quân và Hương đã rút được thẻ ghi số lần lượt là 2 và 5.
Có bao nhiêu sự kiện trong các sự kiện sau không xảy ra?
Sự kiện 1: “Có bạn rút được thẻ số 5”
Sự kiện 2: “Cả hai bạn đều rút được thẻ ghi số lẻ”
Sự kiện 3: “Cả hai bạn đều rút được thẻ ghi số nguyên tố”
Sự kiện 4: “Có đúng một bạn rút được thẻ lớn hơn 3”
1
2
3
4
Đáp án : A
- Xét từng sự kiện.
- Số nguyên tố là số chỉ có ước là 1 và chính nó.
Sự kiện 1: “Có bạn rút được thẻ số 5”
Bạn Quân rút được thẻ số 2 và bạn Hương rút được thẻ số 5.
=> Sự kiện xảy ra.
Sự kiện 2: “Cả hai bạn đều rút được thẻ ghi số lẻ”
Số 2 là số chẵn => Sự kiện không xảy ra.
Sự kiện 3: “Cả hai bạn đều rút được thẻ ghi số nguyên tố”
Số 2 và 5 đều là số nguyên tố => Sự kiện xảy ra.
Sự kiện 4: “Có đúng một bạn rút được thẻ lớn hơn 3”
2<3 và 5>3
=> Có đúng một bạn rút được thẻ lớn hơn 3 là bạn Hương.
=> Sự kiện xảy ra.
Vậy số sự kiện không xảy ra là 1.
Nga quay tấm bìa và thấy mũi tên chỉ vào ô số 3 như hình bên. Hãy cho biết sự kiện nào sau đây xảy ra
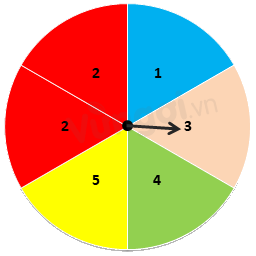
Mũi tên chỉ vào ô ghi số nhỏ hơn 5
Mũi tên chỉ vào ô ghi số 5
Mũi tên chỉ vào ô ghi số lớn hơn 3
Mũi tên chỉ vào ô ghi số chẵn
Đáp án : A
Kiểm tra từng sự kiện.
Mũi tên chỉ vào ô ghi số 3, mà 3<5 nên sự kiện “Mũi tên chỉ vào ô ghi số nhỏ hơn 5” xảy ra.

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là
1. Rút ngẫu nhiên
thẻ;
2. Tập hợp các kết quả có thể xảy ra đối với
xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Viết tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
M={1;2;3;4}
M=(1,2,3,4,5)
M={1,2,3,4}
M={1;2;3;4;5}
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Số xuất hiện trên thẻ được rút có phải là phần tử của tập hợp {1;2;3;4;5} hay không?
Không
Có
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Nêu những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra?
5
1, 2, 3, 4, 5
1, 2, 3
1,2
Cho phép thử nghiệm gieo con xúc xắc 6 mặt. Sự kiện nào trong các sự kiện sau có thể xảy ra:
“Số chấm nhỏ hơn 5”
“Số chấm lớn hơn 6”
“Số chấm bằng 0”
“Số chấm bằng 7”
Phép thử nghiệm: Bạn Ngô chọn một ngày trong tuần để đá bóng. Có tất cả bao nhiêu kết quả có thể xảy ra của phép thử nghiệm này.
5
6
7
4
Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp, hỏi có tất cả bao nhiêu kết quả có thể xảy ra?
1
2
3
4
Trong hộp có 10 lá thư có bì thư giống nhau, bên trong mỗi bì thư có 1 mảnh giấy và được đánh số từ 1 đến 10. Mỗi bạn lấy ngẫu nhiên một bì thư, xem số ghi trên lá thư rồi trả lại vào bì và cho vào hộp. Tập hợp tất cả các kết quả có thể xảy ra là:
\(A = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\)
\(A = \left\{ {10} \right\}\)
\(10\)
\(1\)
Hãy viết tập hợp các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt
\(1;2;3;4;5;6\)
\(Y = 6\)
\(6\)
\(Y = \left\{ {1;2;3;4;5;6} \right\}\)
Tập hợp các kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu là
\(X = \left\{ {N,S} \right\}\)
\(X = \left\{ N \right\}\)
\(X = \left\{ S \right\}\)
\(X = \left\{ {NN,S} \right\}\)
Gieo đồng thời 2 con xúc xắc và nhận được số chấm xuất hiện trên hai con xúc xắc lần lượt là 1 và 5.
Sự kiện nào sau đây xảy ra?
Tổng số chấm xuất hiện trên hai con xúc xắc là số lẻ.
Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 6.
Tổng số chấm xuất hiện trên hai con xúc xắc là số chẵn.
Tổng số chấm xuất hiện trên hai con xúc xắc là bằng 5.
Trong hộp có 10 tấm thẻ ghi các số 2;2;3;3;3;4;5;5;5;5. Yêu cầu 5 bạn lần lượt rút ngẫu nhiên 1 thẻ, quan sát số ghi trên thẻ rồi trả lại thẻ vào hộp. Quân và Hương đã rút được thẻ ghi số lần lượt là 2 và 5.
Có bao nhiêu sự kiện trong các sự kiện sau không xảy ra?
Sự kiện 1: “Có bạn rút được thẻ số 5”
Sự kiện 2: “Cả hai bạn đều rút được thẻ ghi số lẻ”
Sự kiện 3: “Cả hai bạn đều rút được thẻ ghi số nguyên tố”
Sự kiện 4: “Có đúng một bạn rút được thẻ lớn hơn 3”
1
2
3
4
Nga quay tấm bìa và thấy mũi tên chỉ vào ô số 3 như hình bên. Hãy cho biết sự kiện nào sau đây xảy ra

Mũi tên chỉ vào ô ghi số nhỏ hơn 5
Mũi tên chỉ vào ô ghi số 5
Mũi tên chỉ vào ô ghi số lớn hơn 3
Mũi tên chỉ vào ô ghi số chẵn

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là
1. Rút ngẫu nhiên
thẻ;
2. Tập hợp các kết quả có thể xảy ra đối với
xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.
1. Rút ngẫu nhiên
thẻ;
2. Tập hợp các kết quả có thể xảy ra đối với
xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.
Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là
1. Rút ngẫu nhiên 1 thẻ;
2. Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1,2,3,4,5 là các số xuất hiện trên thẻ.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Viết tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
M={1;2;3;4}
M=(1,2,3,4,5)
M={1,2,3,4}
M={1;2;3;4;5}
Đáp án : D
- Tìm các kết quả có thể xảy ra.
- Viết tập hợp: Viết các số trong dấu ngoặc kép { }.
Số có thể xuất hiện trên thẻ là một trong năm số: 1;2;3;4;5.
Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ là
M={1;2;3;4;5}.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Số xuất hiện trên thẻ được rút có phải là phần tử của tập hợp {1;2;3;4;5} hay không?
Không
Có
Có
- Tìm các kết quả có thể xảy ra.
- Số có trong tập hợp là phần tử của tập hợp.
Số có thể xuất hiện trên thẻ là một trong năm số: 1;2;3;4;5.
Các số này đều là phần tử của tập hợp {1;2;3;4;5}.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.
Nêu những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra?
5
1, 2, 3, 4, 5
1, 2, 3
1,2
Đáp án : B
- Tìm các kết quả có thể xảy ra.
Số có thể xuất hiện trên thẻ là một trong năm số: 1;2;3;4;5.
Cho phép thử nghiệm gieo con xúc xắc 6 mặt. Sự kiện nào trong các sự kiện sau có thể xảy ra:
“Số chấm nhỏ hơn 5”
“Số chấm lớn hơn 6”
“Số chấm bằng 0”
“Số chấm bằng 7”
Đáp án : A
Tìm tất các kết quả có thể xảy ra khi gieo xúc xắc.
Kiểm tra sự kiện có thể nằm trong các kết quả đó không.
Các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt là: 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm.
Khi đó số chấm nhỏ hơn 5 có thể xảy ra. Đáp án A đúng.
Số chấm tối đa là 6 nên B sai.
Không có số chấm bằng 0 trong các kết quả có thể xảy ra nên C sai.
Không có số chấm bằng 7 trong các kết quả có thể xảy ra nên D sai.
Phép thử nghiệm: Bạn Ngô chọn một ngày trong tuần để đá bóng. Có tất cả bao nhiêu kết quả có thể xảy ra của phép thử nghiệm này.
5
6
7
4
Đáp án : C
Liệt kê các ngày trong tuần mà Ngô có thể chọn.
Đếm số ngày.
Một tuần có 7 ngày nên Ngô có thể chọn một trong 7 ngày đó để đi đá bóng. Hay số kết quả có thể xảy ra là 7.
Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp, hỏi có tất cả bao nhiêu kết quả có thể xảy ra?
1
2
3
4
Đáp án : B
Tìm tất cả các kết quả có thể xảy ra trong mỗi lần lấy bóng.
Đếm số các kết quả có thể xảy ra.
Các kết quả có thể xảy ra là: (1 xanh + 1 vàng) ; (2 vàng).
Vậy có 2 kết quả có thể xảy ra.
Trong hộp có 10 lá thư có bì thư giống nhau, bên trong mỗi bì thư có 1 mảnh giấy và được đánh số từ 1 đến 10. Mỗi bạn lấy ngẫu nhiên một bì thư, xem số ghi trên lá thư rồi trả lại vào bì và cho vào hộp. Tập hợp tất cả các kết quả có thể xảy ra là:
\(A = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\)
\(A = \left\{ {10} \right\}\)
\(10\)
\(1\)
Đáp án : A
Tìm tất cả các kết quả có thể xảy ra khi lấy ngẫu nhiên.
Viết các kết quả đó trong một tập hợp.
Các số có thể ghi trên lá thư là 1;2;3;4;5;6;7;8;9;10 nên tập hợp tất cả các kết quả có thể xảy ra là \(A = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\)
Hãy viết tập hợp các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt
\(1;2;3;4;5;6\)
\(Y = 6\)
\(6\)
\(Y = \left\{ {1;2;3;4;5;6} \right\}\)
Đáp án : D
Liệt kê các trường hợp của phép thử nghiệm gieo một con xúc xắc 6 mặt.
Viết các kết quả đó trong một tập hợp.
Các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt là: 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm.
Vậy tập hợp cần tìm là \(Y = \left\{ {1;2;3;4;5;6} \right\}\)
Tập hợp các kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu là
\(X = \left\{ {N,S} \right\}\)
\(X = \left\{ N \right\}\)
\(X = \left\{ S \right\}\)
\(X = \left\{ {NN,S} \right\}\)
Đáp án : A
Liệt kê các trường hợp của phép thử nghiệm tung đồng xu.
Phép thử nghiệm tung đồng xu có kết quả có thể là sấp (S) hoặc ngửa (N).
Vậy tập hợp các kết quả có thể xảy ra là \(X = \left\{ {N,S} \right\}\)
Gieo đồng thời 2 con xúc xắc và nhận được số chấm xuất hiện trên hai con xúc xắc lần lượt là 1 và 5.
Sự kiện nào sau đây xảy ra?
Tổng số chấm xuất hiện trên hai con xúc xắc là số lẻ.
Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 6.
Tổng số chấm xuất hiện trên hai con xúc xắc là số chẵn.
Tổng số chấm xuất hiện trên hai con xúc xắc là bằng 5.
Đáp án : C
- Tính tổng số chấm xuất hiện.
- Đối chiếu với đáp án.
Tổng số chấm xuất hiện ở hai con xúc xắc là 1+5=6.
6 là số chẵn nên tổng số chấm xuất hiện trên hai con xúc xắc là số chẵn.
Trong hộp có 10 tấm thẻ ghi các số 2;2;3;3;3;4;5;5;5;5. Yêu cầu 5 bạn lần lượt rút ngẫu nhiên 1 thẻ, quan sát số ghi trên thẻ rồi trả lại thẻ vào hộp. Quân và Hương đã rút được thẻ ghi số lần lượt là 2 và 5.
Có bao nhiêu sự kiện trong các sự kiện sau không xảy ra?
Sự kiện 1: “Có bạn rút được thẻ số 5”
Sự kiện 2: “Cả hai bạn đều rút được thẻ ghi số lẻ”
Sự kiện 3: “Cả hai bạn đều rút được thẻ ghi số nguyên tố”
Sự kiện 4: “Có đúng một bạn rút được thẻ lớn hơn 3”
1
2
3
4
Đáp án : A
- Xét từng sự kiện.
- Số nguyên tố là số chỉ có ước là 1 và chính nó.
Sự kiện 1: “Có bạn rút được thẻ số 5”
Bạn Quân rút được thẻ số 2 và bạn Hương rút được thẻ số 5.
=> Sự kiện xảy ra.
Sự kiện 2: “Cả hai bạn đều rút được thẻ ghi số lẻ”
Số 2 là số chẵn => Sự kiện không xảy ra.
Sự kiện 3: “Cả hai bạn đều rút được thẻ ghi số nguyên tố”
Số 2 và 5 đều là số nguyên tố => Sự kiện xảy ra.
Sự kiện 4: “Có đúng một bạn rút được thẻ lớn hơn 3”
2<3 và 5>3
=> Có đúng một bạn rút được thẻ lớn hơn 3 là bạn Hương.
=> Sự kiện xảy ra.
Vậy số sự kiện không xảy ra là 1.
Nga quay tấm bìa và thấy mũi tên chỉ vào ô số 3 như hình bên. Hãy cho biết sự kiện nào sau đây xảy ra

Mũi tên chỉ vào ô ghi số nhỏ hơn 5
Mũi tên chỉ vào ô ghi số 5
Mũi tên chỉ vào ô ghi số lớn hơn 3
Mũi tên chỉ vào ô ghi số chẵn
Đáp án : A
Kiểm tra từng sự kiện.
Mũi tên chỉ vào ô ghi số 3, mà 3<5 nên sự kiện “Mũi tên chỉ vào ô ghi số nhỏ hơn 5” xảy ra.
Bài 42 Toán 6 Kết nối tri thức tập trung vào việc làm quen với khái niệm về kết quả có thể xảy ra trong một tình huống và sự kiện ngẫu nhiên. Đây là nền tảng quan trọng để học sinh tiếp cận với lý thuyết xác suất trong các lớp học cao hơn.
1. Kết quả có thể: Là những điều có thể xảy ra khi thực hiện một hành động hoặc thí nghiệm. Ví dụ, khi tung một đồng xu, kết quả có thể là mặt ngửa hoặc mặt sấp.
2. Sự kiện: Là một tập hợp các kết quả có thể. Ví dụ, sự kiện “xuất hiện mặt ngửa” bao gồm kết quả duy nhất là mặt ngửa.
3. Không gian mẫu: Là tập hợp tất cả các kết quả có thể xảy ra trong một thí nghiệm. Ví dụ, không gian mẫu khi tung một đồng xu là {ngửa, sấp}.
Ví dụ 1: Một hộp có 5 quả bóng, trong đó có 2 quả bóng màu đỏ, 1 quả bóng màu xanh và 2 quả bóng màu vàng. Lấy ngẫu nhiên một quả bóng từ hộp. Hãy xác định không gian mẫu của thí nghiệm này.
Giải: Không gian mẫu của thí nghiệm là {đỏ, xanh, vàng}.
Ví dụ 2: Tung một con xúc xắc 6 mặt. Xác suất để xuất hiện mặt 5 chấm là bao nhiêu?
Giải: Không gian mẫu của thí nghiệm là {1, 2, 3, 4, 5, 6}. Sự kiện “xuất hiện mặt 5 chấm” bao gồm kết quả duy nhất là 5. Xác suất để xuất hiện mặt 5 chấm là 1/6.
Dưới đây là một số bài tập trắc nghiệm để bạn luyện tập:
Để làm bài trắc nghiệm về chủ đề này hiệu quả, bạn nên:
Kiến thức về kết quả có thể và sự kiện ngẫu nhiên có ứng dụng rộng rãi trong đời sống, chẳng hạn như:
Hy vọng với những kiến thức và bài tập trắc nghiệm trên, các em học sinh lớp 6 sẽ nắm vững kiến thức về bài học "Kết quả có thể và sự kiện trong trò chơi, thí nghiệm" và đạt kết quả tốt trong các bài kiểm tra.
Việc luyện tập thường xuyên với các dạng bài tập khác nhau sẽ giúp các em hiểu sâu sắc hơn về chủ đề này và phát triển tư duy logic, khả năng giải quyết vấn đề.